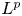1. Introduction
One of the important issues in insurance is insurance pricing. Over the past two decades, researchers have made great efforts to implement appropriate insurance pricing methods. One of the most popular methods is an axiomatic approach to characterize insurance prices, see Wang et al. [Reference Wang, Young and Panjer26]. The insurance pricing can be described as a functional from the set of nonnegative insurance risks to the extended nonnegative real numbers. How to measure the uncertainty is a key problem. “Entropy,” date back to 1865, is one of the best ways to measure uncertainty in probability theory. Shannon [Reference Shannon22] introduced the information entropy of a discrete random variable ![]() $Z$ with probability mass function
$Z$ with probability mass function ![]() $\{p_k\}$ by
$\{p_k\}$ by
which is extended to the case of ![]() $Z$ being a continuous random variable. Closely related to Shannon entropy is the quantity
$Z$ being a continuous random variable. Closely related to Shannon entropy is the quantity
which is called relative entropy (also called Kullback–Leibler divergence), where ![]() $\mathbb {Q} \ll \mathbb {P}$, and
$\mathbb {Q} \ll \mathbb {P}$, and ![]() $\mathbb {Q}$ and
$\mathbb {Q}$ and ![]() $\mathbb {P}$ are two probability measures. Relative entropy has been proved to have close connections with insurance, mathematical finance, risk measures, and others. For example, based on the variational representation of the relative entropy, Föllmer and Schied [Reference Föllmer and Schied11] defined entropic risk measure and studied its properties systemically, Delbaen et al. [Reference Delbaen, Grandits, Rheinländer, Samperi, Schweizer and Stricker8] solved the problem of hedging a contingent claim by maximizing the expected exponential utility of terminal net wealth, and Ahmadi-Javid [Reference Ahmadi-Javid1,Reference Ahmadi-Javid2] defined a new coherent risk measure called the Entropic Value-at-risk (EVaR). There are many generalizations of relative entropy in the literature, such as Rényi divergence [Reference Pichler and Schlotter19,Reference Rényi20] and generalized relative entropy (also called Tsallis relative entropy [Reference Tsallis24,Reference Tsallis25]).
$\mathbb {P}$ are two probability measures. Relative entropy has been proved to have close connections with insurance, mathematical finance, risk measures, and others. For example, based on the variational representation of the relative entropy, Föllmer and Schied [Reference Föllmer and Schied11] defined entropic risk measure and studied its properties systemically, Delbaen et al. [Reference Delbaen, Grandits, Rheinländer, Samperi, Schweizer and Stricker8] solved the problem of hedging a contingent claim by maximizing the expected exponential utility of terminal net wealth, and Ahmadi-Javid [Reference Ahmadi-Javid1,Reference Ahmadi-Javid2] defined a new coherent risk measure called the Entropic Value-at-risk (EVaR). There are many generalizations of relative entropy in the literature, such as Rényi divergence [Reference Pichler and Schlotter19,Reference Rényi20] and generalized relative entropy (also called Tsallis relative entropy [Reference Tsallis24,Reference Tsallis25]).
Recently, Ma and Tian [Reference Ma and Tian16] established a variational representation for the generalized relative entropy, and Tian [Reference Tian23] provided new ideas and insights for pricing the non-attainable contingent claim in incomplete market under the generalized relative entropy. Inspired by these two papers, we propose Tsallis Value-at-Risk (![]() $\mathrm {TsVaR}$) based on Tsallis entropy by following the framework of Ahmadi-Javid [Reference Ahmadi-Javid2] and Ahmadi-Javid and Pichler [Reference Ahmadi-Javid and Pichler4]. As shown by Tsallis [Reference Tsallis25], generalized relative entropy is defined by the generalized
$\mathrm {TsVaR}$) based on Tsallis entropy by following the framework of Ahmadi-Javid [Reference Ahmadi-Javid2] and Ahmadi-Javid and Pichler [Reference Ahmadi-Javid and Pichler4]. As shown by Tsallis [Reference Tsallis25], generalized relative entropy is defined by the generalized ![]() $q$-logarithm and generalized
$q$-logarithm and generalized ![]() $q$-exponential functions. In order to introduce
$q$-exponential functions. In order to introduce ![]() $\mathrm {TsVaR}$ (see Definition 3.1), we restrict ourself to consider nonnegative random variables and
$\mathrm {TsVaR}$ (see Definition 3.1), we restrict ourself to consider nonnegative random variables and ![]() $q\in (0,1]$. Under these restrictions,
$q\in (0,1]$. Under these restrictions, ![]() $\mathrm {TsVaR}$ corresponds to the tightest possible upper bound obtained from the Chernoff inequality for the Value-at-Risk (VaR). We show that
$\mathrm {TsVaR}$ corresponds to the tightest possible upper bound obtained from the Chernoff inequality for the Value-at-Risk (VaR). We show that ![]() $\mathrm {TsVaR}$ is not a coherent premium principle, even not a convex premium principle (see Definition 2.1 for formal definitions). This is caused by a lack of cash invariance in general. We also show that in the class of
$\mathrm {TsVaR}$ is not a coherent premium principle, even not a convex premium principle (see Definition 2.1 for formal definitions). This is caused by a lack of cash invariance in general. We also show that in the class of ![]() $\mathrm {TsVaR}$ with
$\mathrm {TsVaR}$ with ![]() $q \in (0, 1]$, only EVaR is a coherent premium principle. Although
$q \in (0, 1]$, only EVaR is a coherent premium principle. Although ![]() $\mathrm {TsVaR}$ fails to be a convex premium principle,
$\mathrm {TsVaR}$ fails to be a convex premium principle, ![]() $\mathrm {TsVaR}$'s dual representation is an analogy with the generalized relative entropy.
$\mathrm {TsVaR}$'s dual representation is an analogy with the generalized relative entropy.
The motivation of this paper is as follows. The first one is to generalize the concept of EVaR, defined by Ahmadi-Javid [Reference Ahmadi-Javid2], to TsVaR, using the generalized ![]() $q$-logarithm and generalized
$q$-logarithm and generalized ![]() $q$-exponential functions. The second one is to deepen our understanding of the application of entropy in risk measure and premium principle, and to investigate its theoretical properties.
$q$-exponential functions. The second one is to deepen our understanding of the application of entropy in risk measure and premium principle, and to investigate its theoretical properties.
As shown by Pichler [Reference Pichler17,Reference Pichler18], there is an intimate link between norms and coherent risk measures defined on the same model space. Specifically, a coherent risk measure ![]() $\rho$ can be used to define an order-preserving semi-norm on the model space
$\rho$ can be used to define an order-preserving semi-norm on the model space ![]() $\mathcal {X}$ by
$\mathcal {X}$ by ![]() $\|\cdot \|_{\rho }:= \rho (|\cdot |),$ whenever
$\|\cdot \|_{\rho }:= \rho (|\cdot |),$ whenever ![]() $\rho$ is finite over
$\rho$ is finite over ![]() $\mathcal {X}$. Under suitable assumptions on norms, coherent risk measures can be recovered from norms (see [Reference Pichler18] Theorem 3.1). These considerations are also extended to vector-valued random variables (see [Reference Kalmes and Pichler15]).
$\mathcal {X}$. Under suitable assumptions on norms, coherent risk measures can be recovered from norms (see [Reference Pichler18] Theorem 3.1). These considerations are also extended to vector-valued random variables (see [Reference Kalmes and Pichler15]).
Fortunately, when consider the confidence level ![]() $\alpha \in (0,1)$, the norm induced by
$\alpha \in (0,1)$, the norm induced by ![]() $\mathrm {TsVaR}$, called the
$\mathrm {TsVaR}$, called the ![]() $\mathrm {TsVaR}$ norm, is indeed a norm.
$\mathrm {TsVaR}$ norm, is indeed a norm. ![]() $\mathrm {TsVaR}$ norms are proven to be equivalent to each other for different confidence levels, but they do not generate the
$\mathrm {TsVaR}$ norms are proven to be equivalent to each other for different confidence levels, but they do not generate the ![]() $L^p$ norms
$L^p$ norms ![]() $\|\cdot \|_p$. For every
$\|\cdot \|_p$. For every ![]() $1 \lt p \lt (2-q)/(1-q)$, the
$1 \lt p \lt (2-q)/(1-q)$, the ![]() $L^p$ norms are bounded by the
$L^p$ norms are bounded by the ![]() $\mathrm {TsVaR}$ norm, while the converse does not hold true. Thus, the largest model space contained in the domain of
$\mathrm {TsVaR}$ norm, while the converse does not hold true. Thus, the largest model space contained in the domain of ![]() $\mathrm {TsVaR}$ is strictly larger than
$\mathrm {TsVaR}$ is strictly larger than ![]() $L^{\infty }$ but smaller than every
$L^{\infty }$ but smaller than every ![]() $L^p$ space. We also relate the
$L^p$ space. We also relate the ![]() $\mathrm {TsVaR}$ norm to the Orlicz (or Luxemburg) norm on the associated Orlicz space. Orlicz space has been used intensively to study risk measures (see [Reference Cheridito and Li5,Reference Cheridito and Li6]). Finally, we also present closed-form expression for the dual
$\mathrm {TsVaR}$ norm to the Orlicz (or Luxemburg) norm on the associated Orlicz space. Orlicz space has been used intensively to study risk measures (see [Reference Cheridito and Li5,Reference Cheridito and Li6]). Finally, we also present closed-form expression for the dual ![]() $\mathrm {TsVaR}$ norm.
$\mathrm {TsVaR}$ norm.
The remainder of the paper is organized as follows. Section 2 introduces Tsallis relative entropy and premium principle. Section 3 defines the main object ![]() $\mathrm {TsVaR}$ and Tsallis spaces, and provides some basic properties about
$\mathrm {TsVaR}$ and Tsallis spaces, and provides some basic properties about ![]() $\mathrm {TsVaR}$. In Section 4, we first compare Tsallis spaces with other spaces, particularly with the
$\mathrm {TsVaR}$. In Section 4, we first compare Tsallis spaces with other spaces, particularly with the ![]() $L^p$ and Orlicz spaces, and then elaborate duality relations. In this section, we also present the closed formula of the dual
$L^p$ and Orlicz spaces, and then elaborate duality relations. In this section, we also present the closed formula of the dual ![]() $\mathrm {TsVaR}$ norm. Section 5 concludes the paper. Proofs of all lemmas and some propositions are postponed to Appendix A.
$\mathrm {TsVaR}$ norm. Section 5 concludes the paper. Proofs of all lemmas and some propositions are postponed to Appendix A.
2. Preliminaries
2.1. Premium principles
Throughout, we consider an atomless probability space ![]() $(\Omega, \mathscr {F}, \mathbb {P})$. Let
$(\Omega, \mathscr {F}, \mathbb {P})$. Let ![]() $\mathcal {X}$ be a model space, which is used to represent a set of nonnegative random losses. For
$\mathcal {X}$ be a model space, which is used to represent a set of nonnegative random losses. For ![]() $X\in \mathcal {X}$, a positive value of
$X\in \mathcal {X}$, a positive value of ![]() $X$ represents the insurable loss of the insured. Let
$X$ represents the insurable loss of the insured. Let ![]() $L^0_+$ be the set of all nonnegative random variables, and
$L^0_+$ be the set of all nonnegative random variables, and ![]() $L^k_+$ be the set of all random variables in
$L^k_+$ be the set of all random variables in ![]() $L^0_+$ with finite
$L^0_+$ with finite ![]() $k$th moment, where
$k$th moment, where ![]() $k \gt 0$. For
$k \gt 0$. For ![]() $X, Y\in \mathcal {X}$, we write
$X, Y\in \mathcal {X}$, we write ![]() $X\stackrel {\rm d}= Y$ whenever
$X\stackrel {\rm d}= Y$ whenever ![]() $X$ and
$X$ and ![]() $Y$ have the same distribution.
$Y$ have the same distribution.
In this paper, we consider premium principles defined on the model space ![]() $\mathcal {X}$, which are understood as prices of the insurable loss of the insured. A premium principle
$\mathcal {X}$, which are understood as prices of the insurable loss of the insured. A premium principle ![]() $\rho$ is a functional
$\rho$ is a functional ![]() $\rho : {\mathcal {X}} \to \mathbb {R}_+\cup \{+\infty \}$, where
$\rho : {\mathcal {X}} \to \mathbb {R}_+\cup \{+\infty \}$, where ![]() $\mathbb {R}_+=[0,\infty )$.
$\mathbb {R}_+=[0,\infty )$.
Definition 2.1. A mapping ![]() $\rho : {\mathcal {X}} \to \mathbb {R}_+ \cup \{+\infty \}$ is called a convex premium principle if it satisfies the following three properties: for all
$\rho : {\mathcal {X}} \to \mathbb {R}_+ \cup \{+\infty \}$ is called a convex premium principle if it satisfies the following three properties: for all ![]() $X, Y \in {\mathcal {X}}$,
$X, Y \in {\mathcal {X}}$,
(A1) Cash invariance:
 $\rho (X + m) = \rho (X) + m$ for all
$\rho (X + m) = \rho (X) + m$ for all  $m \in \mathbb {R}_+$;
$m \in \mathbb {R}_+$;(A2) Monotonicity:
 $X \le Y \Longrightarrow \rho (X) \le \rho (Y)$;
$X \le Y \Longrightarrow \rho (X) \le \rho (Y)$;(A3) Convexity:
 $\rho (\alpha X + (1-\alpha )Y) \le \alpha \rho (X) + (1-\alpha ) \rho (Y)$ for all
$\rho (\alpha X + (1-\alpha )Y) \le \alpha \rho (X) + (1-\alpha ) \rho (Y)$ for all  $\alpha \in [0,1]$.
$\alpha \in [0,1]$.
A convex premium principle ![]() $\rho$ is called a coherent premium principle if it satisfies
$\rho$ is called a coherent premium principle if it satisfies
(A4) Positive homogeneity:
 $\rho (\lambda X) = \lambda \rho (X)$ for all
$\rho (\lambda X) = \lambda \rho (X)$ for all  $X\in \mathcal {X}$ and
$X\in \mathcal {X}$ and  $\lambda \in \mathbb {R}_+$.
$\lambda \in \mathbb {R}_+$.
In addition, ![]() $\rho$ is said to satisfy law invariance if
$\rho$ is said to satisfy law invariance if ![]() $\rho (X) = \rho (Y)$ whenever
$\rho (X) = \rho (Y)$ whenever ![]() $X\stackrel {\rm d}= Y$. In practice, it is often desirable that we are able to estimate or identify the values of risk premiums statistically, in which case law invariance is a natural requirement. The concepts of convex premium principle and coherent premium principle are analogies with convex risk measure and coherent risk measure [Reference Föllmer and Schied12]. In view of the simplicity and ease of calculation, Value-at-Risk (VaR) is one popular choice of premium principles, defined as
$X\stackrel {\rm d}= Y$. In practice, it is often desirable that we are able to estimate or identify the values of risk premiums statistically, in which case law invariance is a natural requirement. The concepts of convex premium principle and coherent premium principle are analogies with convex risk measure and coherent risk measure [Reference Föllmer and Schied12]. In view of the simplicity and ease of calculation, Value-at-Risk (VaR) is one popular choice of premium principles, defined as
2.2. Tsallis relative entropy
We recall from Tsallis [Reference Tsallis24] the ![]() $q$-generalization of the relative entropy, which is also called Tsallis relative entropy. For any two probability measures
$q$-generalization of the relative entropy, which is also called Tsallis relative entropy. For any two probability measures ![]() $\mathbb {Q}$ and
$\mathbb {Q}$ and ![]() $\mathbb {P}$ on
$\mathbb {P}$ on ![]() $(\Omega, \mathscr {F})$, the
$(\Omega, \mathscr {F})$, the ![]() $q$-generalization of the relative entropy is defined by
$q$-generalization of the relative entropy is defined by
 $$H_q(\mathbb{Q}|\mathbb{P}) := \left\{\begin{array}{ll} \displaystyle \int \left(\dfrac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}}\right)^q \ln_q\left(\dfrac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}}\right)\mathrm{d}\mathbb{P}, & {\rm if}\ \mathbb{Q} \ll \mathbb{P},\\ + \infty, & {\rm otherwise}, \end{array} \right.$$
$$H_q(\mathbb{Q}|\mathbb{P}) := \left\{\begin{array}{ll} \displaystyle \int \left(\dfrac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}}\right)^q \ln_q\left(\dfrac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}}\right)\mathrm{d}\mathbb{P}, & {\rm if}\ \mathbb{Q} \ll \mathbb{P},\\ + \infty, & {\rm otherwise}, \end{array} \right.$$
where ![]() $q \gt 0$, and
$q \gt 0$, and ![]() $\ln _q(x)$ is the generalized
$\ln _q(x)$ is the generalized ![]() $q$-logarithm function defined on
$q$-logarithm function defined on ![]() $(0,\infty )$, given by
$(0,\infty )$, given by
 $$\ln_q(x) := \left\{ \begin{array}{ll} \displaystyle\dfrac{x^{1-q} - 1}{1 - q}, & {\rm for}\ q\ne 1, \\ \ln x, & {\rm for}\ q=1. \end{array} \right.$$
$$\ln_q(x) := \left\{ \begin{array}{ll} \displaystyle\dfrac{x^{1-q} - 1}{1 - q}, & {\rm for}\ q\ne 1, \\ \ln x, & {\rm for}\ q=1. \end{array} \right.$$
The inverse of ![]() $\ln _q(x)$ is called the generalized
$\ln _q(x)$ is called the generalized ![]() $q$-exponential function, given by
$q$-exponential function, given by
 $$\exp_q(x) := \left\{\begin{array}{ll} {[}1+(1-q)x]^{1/(1-q)}, & {\rm for}\ x \gt {-}\dfrac{1}{1-q}\ {\rm and}\ 0 \lt q \lt 1, \\ \left [1+(1-q)x\right ]^{1/(1-q)}, & {\rm for}\ x \lt \dfrac{1}{q-1}\ {\rm and}\ q \gt 1,\\ \exp(x), & {\rm for}\ x\in\mathbb{R}\ {\rm and}\ q=1. \end{array} \right.$$
$$\exp_q(x) := \left\{\begin{array}{ll} {[}1+(1-q)x]^{1/(1-q)}, & {\rm for}\ x \gt {-}\dfrac{1}{1-q}\ {\rm and}\ 0 \lt q \lt 1, \\ \left [1+(1-q)x\right ]^{1/(1-q)}, & {\rm for}\ x \lt \dfrac{1}{q-1}\ {\rm and}\ q \gt 1,\\ \exp(x), & {\rm for}\ x\in\mathbb{R}\ {\rm and}\ q=1. \end{array} \right.$$
Note that ![]() $\ln _q(\cdot )$ and
$\ln _q(\cdot )$ and ![]() $\exp _q(\cdot )$ are well defined when
$\exp _q(\cdot )$ are well defined when ![]() $q \gt 0$. Clearly,
$q \gt 0$. Clearly, ![]() $\ln _1(x)=\ln (x)$,
$\ln _1(x)=\ln (x)$, ![]() $\exp _1(x)=\exp (x)$, and
$\exp _1(x)=\exp (x)$, and ![]() $H_1(\mathbb {Q}\,|\,\mathbb {P})=H(\mathbb {Q}\,|\,\mathbb {P})$, where
$H_1(\mathbb {Q}\,|\,\mathbb {P})=H(\mathbb {Q}\,|\,\mathbb {P})$, where ![]() $H(\mathbb {Q}\,|\,\mathbb {P})$ is defined by (1.1).
$H(\mathbb {Q}\,|\,\mathbb {P})$ is defined by (1.1).
In view of (3.1) and the domains of the function ![]() $\exp _q(x)$ for different
$\exp _q(x)$ for different ![]() $q$, throughout the paper, we always consider the case of
$q$, throughout the paper, we always consider the case of ![]() $0 \lt q \le 1$ unless stated otherwise. In order to accommodate to the domain of
$0 \lt q \le 1$ unless stated otherwise. In order to accommodate to the domain of ![]() $\mathrm {TsVaR}$ (see Definition 3.1), we consider the model space
$\mathrm {TsVaR}$ (see Definition 3.1), we consider the model space ![]() ${\mathcal {X}}=L_+^0$, the space of nonnegative random variables. For recent discussion on risk measures and pricing principles based on Tsallis entropy, we refer to Ma and Tian [Reference Ma and Tian16] and Tian [Reference Tian23].
${\mathcal {X}}=L_+^0$, the space of nonnegative random variables. For recent discussion on risk measures and pricing principles based on Tsallis entropy, we refer to Ma and Tian [Reference Ma and Tian16] and Tian [Reference Tian23].
The next proposition gives some properties of the generalized ![]() $q$-logarithm and
$q$-logarithm and ![]() $q$-exponential functions, which will be helpful for our discussion. For more details, we refer to Tsallis [Reference Tsallis25].
$q$-exponential functions, which will be helpful for our discussion. For more details, we refer to Tsallis [Reference Tsallis25].
Proposition 2.1. The generalized ![]() $q$-logarithm and
$q$-logarithm and ![]() $q$-exponential functions have the following properties:
$q$-exponential functions have the following properties:
(1)
 $\ln _q(\cdot )$ is strictly increasing and concave, and
$\ln _q(\cdot )$ is strictly increasing and concave, and  $\exp _q(\cdot )$ is strictly increasing and convex.
$\exp _q(\cdot )$ is strictly increasing and convex.(2)
 $\ln _q(xy) = x^{1-q}\ln _q(y) + \ln _q(x)$ for all
$\ln _q(xy) = x^{1-q}\ln _q(y) + \ln _q(x)$ for all  $x, y \gt 0$.
$x, y \gt 0$.(3)
 $\ln _q(1/x) = -x^{q-1}\ln _q(x)$ for all
$\ln _q(1/x) = -x^{q-1}\ln _q(x)$ for all  $x \gt 0$.
$x \gt 0$.(4)
 $f(\boldsymbol {x}) := \ln _q (\sum _{i=1}^n \exp _q(x_i))$ is convex in
$f(\boldsymbol {x}) := \ln _q (\sum _{i=1}^n \exp _q(x_i))$ is convex in  $\boldsymbol {x}= (x_1, \dots, x_n)$.
$\boldsymbol {x}= (x_1, \dots, x_n)$.
3. Tsallis value-at-risk
In this section, we propose a new premium principle that corresponds to the tightest possible upper bound obtained from the Chernoff inequality for VaR. The basic idea follows from Chernoff inequality in Chernoff [Reference Chernoff7]: for any constant ![]() $t\in \mathbb {R}_+$ and
$t\in \mathbb {R}_+$ and ![]() $X \in L^0_+$,
$X \in L^0_+$,
By solving the equation
with respect to ![]() $t$ for
$t$ for ![]() $\alpha \in (0,1]$ and
$\alpha \in (0,1]$ and ![]() $\lambda \gt 0$, we obtain
$\lambda \gt 0$, we obtain
which satisfies that ![]() $\mathbb {P}(X \ge t_X(\alpha, \lambda )) \le \alpha$. In fact, for each
$\mathbb {P}(X \ge t_X(\alpha, \lambda )) \le \alpha$. In fact, for each ![]() $\lambda \gt 0$,
$\lambda \gt 0$, ![]() $t_X(\alpha, \lambda )$ is an upper bound for
$t_X(\alpha, \lambda )$ is an upper bound for ![]() ${\rm VaR}_{1-\alpha }(X)$. We now consider the best upper bound of this type as a new premium principle that bounds
${\rm VaR}_{1-\alpha }(X)$. We now consider the best upper bound of this type as a new premium principle that bounds ![]() ${\rm VaR}_{1-\alpha }(\cdot )$ by using the generalized
${\rm VaR}_{1-\alpha }(\cdot )$ by using the generalized ![]() $q$-exponential moments. Recall that we always assume
$q$-exponential moments. Recall that we always assume ![]() $0 \lt q\le 1$ and all random variables in
$0 \lt q\le 1$ and all random variables in ![]() $L^0_+$.
$L^0_+$.
Definition 3.1. Let ![]() $X\in L_+^0$ satisfying that
$X\in L_+^0$ satisfying that ![]() $\mathbb {E} [\exp _q(\lambda _0 X)] \lt \infty$ for some
$\mathbb {E} [\exp _q(\lambda _0 X)] \lt \infty$ for some ![]() $\lambda _0 \gt 0$. Then Tsallis Value-at-Risk
$\lambda _0 \gt 0$. Then Tsallis Value-at-Risk ![]() $(\mathrm {TsVaR})$ of
$(\mathrm {TsVaR})$ of ![]() $X$ with confidence level
$X$ with confidence level ![]() $1-\alpha$ for
$1-\alpha$ for ![]() $\alpha \in (0, 1]$ is defined by
$\alpha \in (0, 1]$ is defined by
Furthermore, define three spaces of random variables
 \begin{align*} E & := \{X \in L_+^0: \mathbb{E}[\exp_q(\lambda X)] \lt \infty \text{ for all}\ \lambda \gt 0\}, \\ E' & := \left\{X \in L_+^0: \frac{q}{1-q}\mathbb{E}[X^{1/q} - X] \lt \infty \right\}, \\ E'' & := \{X \in L_+^0: \mathbb{E}[\exp_q(\lambda X)] \lt \infty \text{ for some}\ \lambda \gt 0\}, \end{align*}
\begin{align*} E & := \{X \in L_+^0: \mathbb{E}[\exp_q(\lambda X)] \lt \infty \text{ for all}\ \lambda \gt 0\}, \\ E' & := \left\{X \in L_+^0: \frac{q}{1-q}\mathbb{E}[X^{1/q} - X] \lt \infty \right\}, \\ E'' & := \{X \in L_+^0: \mathbb{E}[\exp_q(\lambda X)] \lt \infty \text{ for some}\ \lambda \gt 0\}, \end{align*}
which are called the primal, dual, and bidual Tsallis spaces, respectively. For ![]() $q=1$,
$q=1$, ![]() $E'$ is understood as a limiting case, that is,
$E'$ is understood as a limiting case, that is, ![]() $E'=\{X\in L_+^0: \mathbb {E} [X\ln X] \lt \infty \}$, and
$E'=\{X\in L_+^0: \mathbb {E} [X\ln X] \lt \infty \}$, and ![]() $E, E', E''$ are called the primal, dual, and bidual entropic space, respectively. For
$E, E', E''$ are called the primal, dual, and bidual entropic space, respectively. For ![]() $q\in (0,1)$,
$q\in (0,1)$, ![]() $E=E''=L_+^{1/(1-q)}$.
$E=E''=L_+^{1/(1-q)}$.
Remark 3.1 (Lower and upper bounds)
For ![]() $\alpha \in (0,1]$, we have the following bounds for
$\alpha \in (0,1]$, we have the following bounds for ![]() $\mathrm {TsVaR}$:
$\mathrm {TsVaR}$:
To see it, note that ![]() $\exp _q(\cdot )$ is a convex function by Proposition 2.1(1). Applying Jensen's inequality, the above lower bound follows since
$\exp _q(\cdot )$ is a convex function by Proposition 2.1(1). Applying Jensen's inequality, the above lower bound follows since
 \begin{align*} \frac{1}{\lambda} \ln_q \left(\frac{1}{\alpha} \mathbb{E}[\exp_q(\lambda X)]\right) & = \frac{\alpha^{q-1}}{\lambda} \ln_q (\mathbb{E}[\exp_q(\lambda X)]) +\frac{1}{\lambda}\ln_q\left(\frac{1}{\alpha}\right) \\ & \ge \frac{\alpha^{q-1}}{\lambda} \ln_q ([\exp_q(\lambda \mathbb{E} X)]) + \frac{1}{\lambda} \ln_q\left(\frac{1}{\alpha}\right) \ge \alpha^{q-1} \mathbb{E} X. \end{align*}
\begin{align*} \frac{1}{\lambda} \ln_q \left(\frac{1}{\alpha} \mathbb{E}[\exp_q(\lambda X)]\right) & = \frac{\alpha^{q-1}}{\lambda} \ln_q (\mathbb{E}[\exp_q(\lambda X)]) +\frac{1}{\lambda}\ln_q\left(\frac{1}{\alpha}\right) \\ & \ge \frac{\alpha^{q-1}}{\lambda} \ln_q ([\exp_q(\lambda \mathbb{E} X)]) + \frac{1}{\lambda} \ln_q\left(\frac{1}{\alpha}\right) \ge \alpha^{q-1} \mathbb{E} X. \end{align*}
The upper bound follows from
 \begin{align*} \mathrm{TsVaR}_{1-\alpha}(X) & = \inf_{\lambda \gt 0} \left\{ \frac{\alpha^{q-1}}{\lambda} \ln_q (\mathbb{E}[\exp_q(\lambda X)]) + \frac{1}{\lambda} \ln_q \left(\frac{1}{\alpha}\right) \right\} \\ & \le \inf_{\lambda \gt 0} \left\{ \frac{\alpha^{q-1}}{\lambda} \ln_q (\mathbb{E} [\exp_q(\lambda\,\text{ess-sup} (X)) ]) + \frac{1}{\lambda} \ln_q \left(\frac{1}{\alpha}\right) \right\} \\ & = \inf_{\lambda \gt 0} \left\{ \alpha^{q-1}\,\text{ess-sup}(X)+ \frac{1}{\lambda}\ln_q\left(\frac{1}{\alpha}\right) \right\} = \alpha^{q-1}\,\text{ess-sup}(X). \end{align*}
\begin{align*} \mathrm{TsVaR}_{1-\alpha}(X) & = \inf_{\lambda \gt 0} \left\{ \frac{\alpha^{q-1}}{\lambda} \ln_q (\mathbb{E}[\exp_q(\lambda X)]) + \frac{1}{\lambda} \ln_q \left(\frac{1}{\alpha}\right) \right\} \\ & \le \inf_{\lambda \gt 0} \left\{ \frac{\alpha^{q-1}}{\lambda} \ln_q (\mathbb{E} [\exp_q(\lambda\,\text{ess-sup} (X)) ]) + \frac{1}{\lambda} \ln_q \left(\frac{1}{\alpha}\right) \right\} \\ & = \inf_{\lambda \gt 0} \left\{ \alpha^{q-1}\,\text{ess-sup}(X)+ \frac{1}{\lambda}\ln_q\left(\frac{1}{\alpha}\right) \right\} = \alpha^{q-1}\,\text{ess-sup}(X). \end{align*}
From (3.2), it is known that ![]() $\mathrm {TsVaR}_\beta (X)\to +\infty$ as
$\mathrm {TsVaR}_\beta (X)\to +\infty$ as ![]() $\beta \nearrow 1$ when
$\beta \nearrow 1$ when ![]() $\mathbb {E} [X] \gt 0$ and
$\mathbb {E} [X] \gt 0$ and ![]() $0 \lt q \lt 1$. So, in Definition 3.1, we can not assume
$0 \lt q \lt 1$. So, in Definition 3.1, we can not assume ![]() $\mathrm {TsVaR}_1(X)=\text {ess-sup}(X)$ for
$\mathrm {TsVaR}_1(X)=\text {ess-sup}(X)$ for ![]() $X\in E''$ except
$X\in E''$ except ![]() $\mathrm {EVaR}_1(X)=\text {ess-sup}(X)$.
$\mathrm {EVaR}_1(X)=\text {ess-sup}(X)$.
Below, we will see that ![]() $\mathrm {TsVaR}$ can not be a coherent premium principle, even for convex premium principle unless
$\mathrm {TsVaR}$ can not be a coherent premium principle, even for convex premium principle unless ![]() $q = 1$, since
$q = 1$, since ![]() $\mathrm {TsVaR}$ is not cash invariance in general. To prove the convexity of
$\mathrm {TsVaR}$ is not cash invariance in general. To prove the convexity of ![]() $\mathrm {TsVaR}_{1-\alpha }(\cdot )$, we need the following two lemmas.
$\mathrm {TsVaR}_{1-\alpha }(\cdot )$, we need the following two lemmas.
Lemma 3.2. For ![]() $0 \lt q\le 1$ and
$0 \lt q\le 1$ and ![]() $\alpha \in (0,1]$, the function
$\alpha \in (0,1]$, the function ![]() $g_{\alpha }(X,\lambda ):= t_X(\alpha, 1/\lambda )$ is convex in
$g_{\alpha }(X,\lambda ):= t_X(\alpha, 1/\lambda )$ is convex in ![]() $(X, \lambda )$, where
$(X, \lambda )$, where ![]() $\lambda \gt 0$ and
$\lambda \gt 0$ and ![]() $X\in E''$.
$X\in E''$.
Lemma 3.3. For ![]() $0 \lt q\le 1$ and
$0 \lt q\le 1$ and ![]() $\alpha \in (0,1]$, the function
$\alpha \in (0,1]$, the function ![]() $\inf _{\lambda \gt 0} \big \{g_{\alpha }(X,\lambda )\}$ is convex in
$\inf _{\lambda \gt 0} \big \{g_{\alpha }(X,\lambda )\}$ is convex in ![]() $X \in E''$.
$X \in E''$.
Proposition 3.4. ![]() $\mathrm {TsVaR}_{1-\alpha }(\cdot )$ defined on
$\mathrm {TsVaR}_{1-\alpha }(\cdot )$ defined on ![]() $E''$ is a law invariant, monotonicity, positive homogeneity, and convex functional for every
$E''$ is a law invariant, monotonicity, positive homogeneity, and convex functional for every ![]() $\alpha \in (0,1]$.
$\alpha \in (0,1]$.
Proof. Note that ![]() $\mathrm {TsVaR}_{1-\alpha }(X)= \inf _{\lambda \gt 0} \{ g_{\alpha }(X,\lambda ) \}$. The convexity of
$\mathrm {TsVaR}_{1-\alpha }(X)= \inf _{\lambda \gt 0} \{ g_{\alpha }(X,\lambda ) \}$. The convexity of ![]() $\mathrm {TsVaR}_{1-\alpha }(\cdot )$ follows from Lemma 3.3. The law invariant, monotonicity, and positive homogeneity are obvious.
$\mathrm {TsVaR}_{1-\alpha }(\cdot )$ follows from Lemma 3.3. The law invariant, monotonicity, and positive homogeneity are obvious.
![]() $\mathrm {TsVaR}_{1-\alpha }(\cdot )$ is also subadditive on
$\mathrm {TsVaR}_{1-\alpha }(\cdot )$ is also subadditive on ![]() $E''$, that is,
$E''$, that is,
because ![]() $\mathrm {TsVaR}_{1-\alpha }(0)=0$, and convexity is equivalent to subadditivity under positive homogeneity. However, in general,
$\mathrm {TsVaR}_{1-\alpha }(0)=0$, and convexity is equivalent to subadditivity under positive homogeneity. However, in general, ![]() $\mathrm {TsVaR}_{1-\alpha }(\cdot )$ may fail to satisfy cash invariance. In Proposition 3.9, we will show that
$\mathrm {TsVaR}_{1-\alpha }(\cdot )$ may fail to satisfy cash invariance. In Proposition 3.9, we will show that ![]() $\mathrm {TsVaR}_{1-\alpha }(\cdot )$ possesses some certain cash-subadditivity.
$\mathrm {TsVaR}_{1-\alpha }(\cdot )$ possesses some certain cash-subadditivity.
In the following theorem, we show that ![]() $\mathrm {TsVaR}_{1-\alpha }(\cdot )$ is a coherent premium principle if and only if
$\mathrm {TsVaR}_{1-\alpha }(\cdot )$ is a coherent premium principle if and only if ![]() $q = 1$. In other words, with the exception of EVaR,
$q = 1$. In other words, with the exception of EVaR, ![]() $\mathrm {TsVaR}$ is not a coherent premium principle. EVaR is defined by (see [Reference Ahmadi-Javid2])
$\mathrm {TsVaR}$ is not a coherent premium principle. EVaR is defined by (see [Reference Ahmadi-Javid2])
Theorem 3.5. For ![]() $q\in (0,1]$,
$q\in (0,1]$, ![]() $\mathrm {TsVaR}_{1-\alpha }(\cdot )$ is a coherent premium principle for each
$\mathrm {TsVaR}_{1-\alpha }(\cdot )$ is a coherent premium principle for each ![]() $\alpha \in (0,1]$ if and only if
$\alpha \in (0,1]$ if and only if ![]() $q=1$.
$q=1$.
Proof. Sufficiency. When ![]() $q=1$,
$q=1$, ![]() $\mathrm {TsVaR}$ reduces to EVaR, which has been proven to be coherent by Ahmadi-Javid [Reference Ahmadi-Javid2].
$\mathrm {TsVaR}$ reduces to EVaR, which has been proven to be coherent by Ahmadi-Javid [Reference Ahmadi-Javid2].
Necessary. Assume that ![]() $\mathrm {TsVaR}_{1-\alpha }(\cdot )$ is coherent for each
$\mathrm {TsVaR}_{1-\alpha }(\cdot )$ is coherent for each ![]() $\alpha \in (0,1]$. Then, for any
$\alpha \in (0,1]$. Then, for any ![]() $m \in \mathbb {R}_+$ and
$m \in \mathbb {R}_+$ and ![]() $\alpha \in (0,1]$, we have
$\alpha \in (0,1]$, we have ![]() $\mathrm {TsVaR}_{1-\alpha }(X+m) = \mathrm {TsVaR}_{1-\alpha }(X)+m$. Choose
$\mathrm {TsVaR}_{1-\alpha }(X+m) = \mathrm {TsVaR}_{1-\alpha }(X)+m$. Choose ![]() $X \equiv c\in \mathbb {R}_+$. From (3.1), it follows that
$X \equiv c\in \mathbb {R}_+$. From (3.1), it follows that
 \begin{align*} \mathrm{TsVaR}_{1-\alpha} (c + m) & = \inf_{\lambda \gt 0} \left\{\frac{1}{\lambda} \ln_q \left(\frac{1}{\alpha} \exp_q(\lambda(c+m))\right)\right\} \\ & = \inf_{\lambda \gt 0} \left\{\alpha^{q-1}(c+m)+\frac{1}{\lambda}\ln_q \left(\frac{1}{\alpha}\right)\right\} =\alpha^{q-1} (c+m), \end{align*}
\begin{align*} \mathrm{TsVaR}_{1-\alpha} (c + m) & = \inf_{\lambda \gt 0} \left\{\frac{1}{\lambda} \ln_q \left(\frac{1}{\alpha} \exp_q(\lambda(c+m))\right)\right\} \\ & = \inf_{\lambda \gt 0} \left\{\alpha^{q-1}(c+m)+\frac{1}{\lambda}\ln_q \left(\frac{1}{\alpha}\right)\right\} =\alpha^{q-1} (c+m), \end{align*}
and
 \begin{align*} \mathrm{TsVaR}_{1-\alpha} (c)+ m & = \inf_{\lambda \gt 0} \left\{\frac{1}{\lambda} \ln_q\left(\frac{1}{\alpha} \exp_q(\lambda c)\right)\right\}+m \\ & = \inf_{\lambda \gt 0} \left\{\alpha^{q-1} c+\frac{1}{\lambda} \ln_q \left(\frac{1}{\alpha}\right) \right\}+m =\alpha^{q-1} c+m, \end{align*}
\begin{align*} \mathrm{TsVaR}_{1-\alpha} (c)+ m & = \inf_{\lambda \gt 0} \left\{\frac{1}{\lambda} \ln_q\left(\frac{1}{\alpha} \exp_q(\lambda c)\right)\right\}+m \\ & = \inf_{\lambda \gt 0} \left\{\alpha^{q-1} c+\frac{1}{\lambda} \ln_q \left(\frac{1}{\alpha}\right) \right\}+m =\alpha^{q-1} c+m, \end{align*}
Thus, ![]() $\alpha ^{q-1}(c+m) = \alpha ^{q-1} c+m$ for any
$\alpha ^{q-1}(c+m) = \alpha ^{q-1} c+m$ for any ![]() $m\in \mathbb {R}_+$ and
$m\in \mathbb {R}_+$ and ![]() $\alpha \in (0,1)$. This implies
$\alpha \in (0,1)$. This implies ![]() $q=1$.
$q=1$.
Although ![]() $\mathrm {TsVaR}$ is not a coherent premium principle in general, we establish its dual representation, which reveals its relationship with the generalized relative entropy. To state and prove this result, we need two lemmas. The first one is the variational representation for the generalized relative entropy, and the second one is a special case of Lemma 1.3 in Ahmadi-Javid [Reference Ahmadi-Javid1].
$\mathrm {TsVaR}$ is not a coherent premium principle in general, we establish its dual representation, which reveals its relationship with the generalized relative entropy. To state and prove this result, we need two lemmas. The first one is the variational representation for the generalized relative entropy, and the second one is a special case of Lemma 1.3 in Ahmadi-Javid [Reference Ahmadi-Javid1].
Lemma 3.6. [Reference Ma and Tian16] Theorem 4.1
For ![]() $\lambda \gt 0,\ q \gt 0$, and
$\lambda \gt 0,\ q \gt 0$, and ![]() $q\ne 1$, we have
$q\ne 1$, we have
Lemma 3.7. For ![]() $0 \lt q\le 1$ and
$0 \lt q\le 1$ and ![]() $\alpha \in (0, 1]$,
$\alpha \in (0, 1]$,
 \begin{align} & \inf_{\lambda \gt 0} \left\{ \sup_{\mathbb{Q} \ll \mathbb{P}} \left\{\mathbb{E}\left[\left(\frac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}} \right)^q X \right] + \lambda \left(\alpha^{1-q} \ln_q \left(\frac{1}{\alpha}\right) - H_q(\mathbb{Q}|\mathbb{P}) \right) \right\} \right\} \nonumber\\ & \quad = \sup_{\mathbb{Q} \ll \mathbb{P}, H_q(\mathbb{Q}|\mathbb{P}) \le -\ln_q(\alpha)} \mathbb{E}\left[\left(\frac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}} \right)^q X\right], \quad X\in E''. \end{align}
\begin{align} & \inf_{\lambda \gt 0} \left\{ \sup_{\mathbb{Q} \ll \mathbb{P}} \left\{\mathbb{E}\left[\left(\frac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}} \right)^q X \right] + \lambda \left(\alpha^{1-q} \ln_q \left(\frac{1}{\alpha}\right) - H_q(\mathbb{Q}|\mathbb{P}) \right) \right\} \right\} \nonumber\\ & \quad = \sup_{\mathbb{Q} \ll \mathbb{P}, H_q(\mathbb{Q}|\mathbb{P}) \le -\ln_q(\alpha)} \mathbb{E}\left[\left(\frac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}} \right)^q X\right], \quad X\in E''. \end{align}
Theorem 3.8. For ![]() $0 \lt q\le 1$, the dual representation of
$0 \lt q\le 1$, the dual representation of ![]() $\mathrm {TsVaR}_{1-\alpha }$ has the form
$\mathrm {TsVaR}_{1-\alpha }$ has the form
where ![]() ${\mathcal {Q}} = \{\mathbb {Q} \ll \mathbb {P}: H_q(\mathbb {Q}|\mathbb {P}) \le -\ln _q(\alpha )\}$.
${\mathcal {Q}} = \{\mathbb {Q} \ll \mathbb {P}: H_q(\mathbb {Q}|\mathbb {P}) \le -\ln _q(\alpha )\}$.
Proof. For ![]() $q=1$,
$q=1$, ![]() $\mathrm {TsVaR}$ is EVaR, and the corresponding proof can be found in Ahmadi-Javid [Reference Ahmadi-Javid2]. For
$\mathrm {TsVaR}$ is EVaR, and the corresponding proof can be found in Ahmadi-Javid [Reference Ahmadi-Javid2]. For ![]() $q \in (0,1)$ and
$q \in (0,1)$ and ![]() $X\in E''$, by Proposition 2.1(2) and Lemmas 3.6 and 3.7, we have
$X\in E''$, by Proposition 2.1(2) and Lemmas 3.6 and 3.7, we have
 \begin{align*} \mathrm{TsVaR}_{1-\alpha}(X) & =\inf_{\lambda \gt 0} \left\{ \frac{1}{\lambda} \ln_q \left(\frac{1}{\alpha} \mathbb{E}[\exp_q(\lambda X)]\right) \right\} \\ & = \inf_{\lambda \gt 0} \left\{\frac{1}{\lambda} \left( \alpha^{q-1} \ln_q \mathbb{E}[\exp_q(\lambda X)] + \ln_q \frac{1}{\alpha} \right) \right\} \\ & =\inf_{\lambda \gt 0} \left\{ \frac{1}{\lambda} \left(\alpha^{q-1} \sup_{\mathbb{Q} \ll \mathbb{P}} \left\{\lambda \, \mathbb{E}\left[\left(\frac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}}\right)^q X \right] - H_q(\mathbb{Q}|\mathbb{P})\right\} + \ln_q \left(\frac{1}{\alpha}\right) \right) \right\} \\ & = \inf_{\lambda \gt 0} \left\{ \sup_{\mathbb{Q} \ll \mathbb{P}} \left\{ \alpha^{q-1}\mathbb{E}\left[\left(\frac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}}\right)^q X \right] - \frac{1}{\lambda} \left [\alpha^{q-1} H_q(\mathbb{Q}|\mathbb{P}) - \ln_q\left(\frac{1}{\alpha}\right)\right ] \right\} \right\} \\ & =\sup_{\mathbb{Q} \ll \mathbb{P}, H_q(\mathbb{Q}|\mathbb{P}) \le -\ln_q(\alpha)} \left\{ \alpha^{q-1}\mathbb{E}\left[\left(\frac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}}\right)^q X \right] \right\}. \end{align*}
\begin{align*} \mathrm{TsVaR}_{1-\alpha}(X) & =\inf_{\lambda \gt 0} \left\{ \frac{1}{\lambda} \ln_q \left(\frac{1}{\alpha} \mathbb{E}[\exp_q(\lambda X)]\right) \right\} \\ & = \inf_{\lambda \gt 0} \left\{\frac{1}{\lambda} \left( \alpha^{q-1} \ln_q \mathbb{E}[\exp_q(\lambda X)] + \ln_q \frac{1}{\alpha} \right) \right\} \\ & =\inf_{\lambda \gt 0} \left\{ \frac{1}{\lambda} \left(\alpha^{q-1} \sup_{\mathbb{Q} \ll \mathbb{P}} \left\{\lambda \, \mathbb{E}\left[\left(\frac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}}\right)^q X \right] - H_q(\mathbb{Q}|\mathbb{P})\right\} + \ln_q \left(\frac{1}{\alpha}\right) \right) \right\} \\ & = \inf_{\lambda \gt 0} \left\{ \sup_{\mathbb{Q} \ll \mathbb{P}} \left\{ \alpha^{q-1}\mathbb{E}\left[\left(\frac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}}\right)^q X \right] - \frac{1}{\lambda} \left [\alpha^{q-1} H_q(\mathbb{Q}|\mathbb{P}) - \ln_q\left(\frac{1}{\alpha}\right)\right ] \right\} \right\} \\ & =\sup_{\mathbb{Q} \ll \mathbb{P}, H_q(\mathbb{Q}|\mathbb{P}) \le -\ln_q(\alpha)} \left\{ \alpha^{q-1}\mathbb{E}\left[\left(\frac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}}\right)^q X \right] \right\}. \end{align*}
The desired result now follows.
By Theorem 3.8, we will show in the next proposition that ![]() $\mathrm {TsVaR}_{1-\alpha }(\cdot )$ satisfies some restricted cash-subadditivity. For more discussion on cash-subadditivity, we refer to El Karoui and Ravanelli [Reference El Karoui and Ravanelli10] and Han et al. [Reference Han, Wang, Wang and Xia13].
$\mathrm {TsVaR}_{1-\alpha }(\cdot )$ satisfies some restricted cash-subadditivity. For more discussion on cash-subadditivity, we refer to El Karoui and Ravanelli [Reference El Karoui and Ravanelli10] and Han et al. [Reference Han, Wang, Wang and Xia13].
Proposition 3.9. For ![]() $0 \lt q\le 1$ and
$0 \lt q\le 1$ and ![]() $\alpha \in (0,1]$, we have
$\alpha \in (0,1]$, we have
Proof. By Theorem 3.8, we have
where ![]() ${\mathcal {Q}} = \{\mathbb {Q} \ll \mathbb {P}: H_q(\mathbb {Q}|\mathbb {P}) \le -\ln _q(\alpha )\}.$ Then,
${\mathcal {Q}} = \{\mathbb {Q} \ll \mathbb {P}: H_q(\mathbb {Q}|\mathbb {P}) \le -\ln _q(\alpha )\}.$ Then,
 \begin{align*} \mathrm{TsVaR}_{1-\alpha}(X + m) & = \sup_{\mathbb{Q} \in {\mathcal{Q}}} \left\{ \alpha^{q-1}\mathbb{E}\left[\left(\frac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}}\right)^q (X+m) \right] \right\} \\ & = \sup_{\mathbb{Q} \in {\mathcal{Q}}} \left\{ \alpha^{q-1}\mathbb{E}\left[\left(\frac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}}\right)^q X\right] +m \alpha^{q-1}\mathbb{E}\left[\left(\frac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}}\right)^q \right]\right\} \\ & \le \sup_{\mathbb{Q} \in {\mathcal{Q}}} \left\{ \alpha^{q-1}\mathbb{E}\left[\left(\frac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}}\right)^q X\right] +m \alpha^{q-1}\left[\mathbb{E}\left(\frac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}}\right) \right]^q \right\} \\ & = \mathrm{TsVaR}_{1-\alpha}(X)+ \alpha^{q-1}m, \end{align*}
\begin{align*} \mathrm{TsVaR}_{1-\alpha}(X + m) & = \sup_{\mathbb{Q} \in {\mathcal{Q}}} \left\{ \alpha^{q-1}\mathbb{E}\left[\left(\frac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}}\right)^q (X+m) \right] \right\} \\ & = \sup_{\mathbb{Q} \in {\mathcal{Q}}} \left\{ \alpha^{q-1}\mathbb{E}\left[\left(\frac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}}\right)^q X\right] +m \alpha^{q-1}\mathbb{E}\left[\left(\frac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}}\right)^q \right]\right\} \\ & \le \sup_{\mathbb{Q} \in {\mathcal{Q}}} \left\{ \alpha^{q-1}\mathbb{E}\left[\left(\frac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}}\right)^q X\right] +m \alpha^{q-1}\left[\mathbb{E}\left(\frac{\mathrm{d}\mathbb{Q}}{\mathrm{d}\mathbb{P}}\right) \right]^q \right\} \\ & = \mathrm{TsVaR}_{1-\alpha}(X)+ \alpha^{q-1}m, \end{align*}
where the inequality follows from Jensen's inequality.
From Definition 3.1, it follows that
 \begin{align*} \mathrm{TsVaR}_{1-\alpha}(X) & = \inf_{\lambda \gt 0} \left\{ \frac{1}{\lambda} \ln_q \left(\frac{1}{\alpha} \mathbb{E}[\exp_q(\lambda X)]\right) \right\}\\ & = \inf_{\lambda \gt 0} \left\{ \frac{1}{\lambda} \alpha^{q-1} \ln_q (\mathbb{E}[\exp_q(\lambda X)]) + \frac{1}{\lambda} \ln_q \left(\frac{1}{\alpha}\right) \right\} \\ & =\inf_{\lambda \gt 0} \left\{ \frac{1}{\lambda} \alpha^{q-1} \ln_q (\mathbb{E}[\exp_q(\lambda X)]) - \frac{1}{\lambda} \alpha^{q-1} \ln_q (\alpha) \right\}, \end{align*}
\begin{align*} \mathrm{TsVaR}_{1-\alpha}(X) & = \inf_{\lambda \gt 0} \left\{ \frac{1}{\lambda} \ln_q \left(\frac{1}{\alpha} \mathbb{E}[\exp_q(\lambda X)]\right) \right\}\\ & = \inf_{\lambda \gt 0} \left\{ \frac{1}{\lambda} \alpha^{q-1} \ln_q (\mathbb{E}[\exp_q(\lambda X)]) + \frac{1}{\lambda} \ln_q \left(\frac{1}{\alpha}\right) \right\} \\ & =\inf_{\lambda \gt 0} \left\{ \frac{1}{\lambda} \alpha^{q-1} \ln_q (\mathbb{E}[\exp_q(\lambda X)]) - \frac{1}{\lambda} \alpha^{q-1} \ln_q (\alpha) \right\}, \end{align*}
which shows that ![]() $\mathrm {TsVaR}_{1-\alpha }(X)$ only depends on
$\mathrm {TsVaR}_{1-\alpha }(X)$ only depends on ![]() $\{\ln _q \mathbb {E}[\exp _q(\lambda X)], \lambda \gt 0\}$. The next proposition demonstrates how these functions can be represented by means of
$\{\ln _q \mathbb {E}[\exp _q(\lambda X)], \lambda \gt 0\}$. The next proposition demonstrates how these functions can be represented by means of ![]() $\mathrm {TsVaR}$.
$\mathrm {TsVaR}$.
Proposition 3.10. For ![]() $X \in E$ and
$X \in E$ and ![]() $\lambda \gt 0$,
$\lambda \gt 0$,
 \begin{align} \ln_q \mathbb{E}[\exp_q(\lambda X)] & = \sup_{0 \lt \alpha \le 1} \{ \lambda \alpha^{1-q} \mathrm{TsVaR}_{1-\alpha}(X) + \ln_q (\alpha) \}, \\ \mathbb{E}[\exp_q(\lambda X)] & = \sup_{0 \lt \alpha \le 1} \exp_q( \lambda \alpha^{1-q}\mathrm{TsVaR}_{1-\alpha}(X) + \ln_q (\alpha) ), \nonumber\\ t_X(1,\lambda) & = \sup_{0 \lt \alpha \le 1} \{ \alpha^{1-q} \mathrm{TsVaR}_{1-\alpha}(X) + \lambda^{{-}1} \ln_q (\alpha) \}. \nonumber \end{align}
\begin{align} \ln_q \mathbb{E}[\exp_q(\lambda X)] & = \sup_{0 \lt \alpha \le 1} \{ \lambda \alpha^{1-q} \mathrm{TsVaR}_{1-\alpha}(X) + \ln_q (\alpha) \}, \\ \mathbb{E}[\exp_q(\lambda X)] & = \sup_{0 \lt \alpha \le 1} \exp_q( \lambda \alpha^{1-q}\mathrm{TsVaR}_{1-\alpha}(X) + \ln_q (\alpha) ), \nonumber\\ t_X(1,\lambda) & = \sup_{0 \lt \alpha \le 1} \{ \alpha^{1-q} \mathrm{TsVaR}_{1-\alpha}(X) + \lambda^{{-}1} \ln_q (\alpha) \}. \nonumber \end{align}
Proof. We only prove (3.6). By Proposition 2.1(2), we have
 \begin{align*} -\mathrm{TsVaR}_{1-\alpha}(X) & = \sup_{x \gt 0} \left\{{-}x \ln_q \left (\frac{1}{\alpha} \mathbb{E}\left [\exp_q\left(\frac{X}{x}\right) \right ]\right ) \right\} \\ & = \sup_{x \gt 0} \left\{{-}x \ln_q \left(\frac{1}{\alpha}\right) - x \alpha^{q-1}\ln_q \mathbb{E}\left [\exp_q\left(\frac{X}{x}\right)\right] \right\}. \end{align*}
\begin{align*} -\mathrm{TsVaR}_{1-\alpha}(X) & = \sup_{x \gt 0} \left\{{-}x \ln_q \left (\frac{1}{\alpha} \mathbb{E}\left [\exp_q\left(\frac{X}{x}\right) \right ]\right ) \right\} \\ & = \sup_{x \gt 0} \left\{{-}x \ln_q \left(\frac{1}{\alpha}\right) - x \alpha^{q-1}\ln_q \mathbb{E}\left [\exp_q\left(\frac{X}{x}\right)\right] \right\}. \end{align*}
Thus,
 \begin{align*} -\alpha^{1-q} \mathrm{TsVaR}_{1-\alpha}(X) & = \sup_{x \gt 0} \left\{{-}x \alpha^{1-q} \ln_q \left(\frac{1}{\alpha}\right) - x \ln_q \mathbb{E}\left[\exp_q\left(\frac{X}{x}\right)\right] \right\}\\ & = \sup_{x \gt 0} \left\{ x \ln_q (\alpha) - x \ln_q \mathbb{E}\left[\exp_q\left(\frac{X}{x}\right)\right] \right\} \\ & = \sup_{x \ge 0} \{ x \ln_q (\alpha) - g(x) \}, \end{align*}
\begin{align*} -\alpha^{1-q} \mathrm{TsVaR}_{1-\alpha}(X) & = \sup_{x \gt 0} \left\{{-}x \alpha^{1-q} \ln_q \left(\frac{1}{\alpha}\right) - x \ln_q \mathbb{E}\left[\exp_q\left(\frac{X}{x}\right)\right] \right\}\\ & = \sup_{x \gt 0} \left\{ x \ln_q (\alpha) - x \ln_q \mathbb{E}\left[\exp_q\left(\frac{X}{x}\right)\right] \right\} \\ & = \sup_{x \ge 0} \{ x \ln_q (\alpha) - g(x) \}, \end{align*}
where
One can observe that the function ![]() $-[\exp _q(y)]^{1-q} \mathrm {TsVaR}_{1-\exp _q(y)}(X)$ with domain
$-[\exp _q(y)]^{1-q} \mathrm {TsVaR}_{1-\exp _q(y)}(X)$ with domain ![]() $(-1/(1-q), 0]$ for
$(-1/(1-q), 0]$ for ![]() $0 \lt q \lt 1$ and
$0 \lt q \lt 1$ and ![]() $(-\infty, 0]$ for
$(-\infty, 0]$ for ![]() $q=1$ is the conjugate of function
$q=1$ is the conjugate of function ![]() $g(x)$ with domain
$g(x)$ with domain ![]() $[0,+\infty )$. Since
$[0,+\infty )$. Since ![]() $g(x)$ is convex and closed by Lemma 3.2,
$g(x)$ is convex and closed by Lemma 3.2, ![]() $g(x)$ is the conjugate of its own conjugate. This completes the proof.
$g(x)$ is the conjugate of its own conjugate. This completes the proof.
The next proposition compares the values of ![]() $\mathrm {TsVaR}$ for different confidence levels
$\mathrm {TsVaR}$ for different confidence levels ![]() $\alpha$.
$\alpha$.
Proposition 3.11. For ![]() $0 \lt \alpha _1 \le \alpha _2 \lt 1$,
$0 \lt \alpha _1 \le \alpha _2 \lt 1$, ![]() $q \in (0, 1]$, we have
$q \in (0, 1]$, we have
and
Proof. The proof of the case ![]() $q=1$ can be found in Proposition 2.12 of Ahmadi-Javid and Pichler [Reference Ahmadi-Javid and Pichler4]. Next, we assume
$q=1$ can be found in Proposition 2.12 of Ahmadi-Javid and Pichler [Reference Ahmadi-Javid and Pichler4]. Next, we assume ![]() $q \in (0,1)$. Note that
$q \in (0,1)$. Note that
 \begin{align*} \frac{1}{\lambda} \ln_q \left[\frac{1}{\alpha_1} \mathbb{E}[\exp_q(\lambda X)]\right] & = \frac{1}{\lambda} \ln_q \left(\frac{\alpha_2}{\alpha_1} \frac{1}{\alpha_2} \mathbb{E}[\exp_q(\lambda X)]\right) \\ & =\frac{1}{\lambda}\left(\frac{\alpha_2}{\alpha_1}\right)^{1-q} \ln_q \left(\frac{1}{\alpha_2} \mathbb{E}[\exp_q(\lambda X)]\right) + \frac{1}{\lambda} \ln_q \left(\frac{\alpha_2}{\alpha_1}\right) \\ & \ge \frac{1}{\lambda} \left(\frac{\alpha_2}{\alpha_1}\right)^{1-q} \ln_q \left(\frac{1}{\alpha_2} \mathbb{E}[\exp_q(\lambda X)]\right). \end{align*}
\begin{align*} \frac{1}{\lambda} \ln_q \left[\frac{1}{\alpha_1} \mathbb{E}[\exp_q(\lambda X)]\right] & = \frac{1}{\lambda} \ln_q \left(\frac{\alpha_2}{\alpha_1} \frac{1}{\alpha_2} \mathbb{E}[\exp_q(\lambda X)]\right) \\ & =\frac{1}{\lambda}\left(\frac{\alpha_2}{\alpha_1}\right)^{1-q} \ln_q \left(\frac{1}{\alpha_2} \mathbb{E}[\exp_q(\lambda X)]\right) + \frac{1}{\lambda} \ln_q \left(\frac{\alpha_2}{\alpha_1}\right) \\ & \ge \frac{1}{\lambda} \left(\frac{\alpha_2}{\alpha_1}\right)^{1-q} \ln_q \left(\frac{1}{\alpha_2} \mathbb{E}[\exp_q(\lambda X)]\right). \end{align*}
Then, taking the infimum over ![]() $\lambda \gt 0$ in the both sides of the above inequality yields that
$\lambda \gt 0$ in the both sides of the above inequality yields that
This proves (3.7).
To prove (3.8), note that ![]() $\ln _q \mathbb {E}[\exp _q(\lambda X)] \ge 0$ since
$\ln _q \mathbb {E}[\exp _q(\lambda X)] \ge 0$ since ![]() $X\ge 0$. Thus, for
$X\ge 0$. Thus, for ![]() $q \in (0, 1)$, we have
$q \in (0, 1)$, we have
 \begin{align} \frac{1}{\lambda}\ln_q \left[\frac{1}{\alpha_1} \mathbb{E}[\exp_q(\lambda X)]\right] & = \frac{1}{\lambda}\alpha_1^{q-1}\ln_q \mathbb{E}[\exp_q(\lambda X)] + \frac{1}{\lambda}\ln_q \left(\frac{1}{\alpha_1}\right) \nonumber\\ & = \frac{1}{\lambda}\frac{\alpha_1^{q-1}}{\alpha_2^{q-1}} \alpha_2^{q-1}\ln_q \mathbb{E}[\exp_q(\lambda X)] + \frac{1}{\lambda}\frac{\ln_q (\alpha_1^{{-}1})}{\ln_q (\alpha_2^{{-}1})} \ln_q \left(\frac{1}{\alpha_2}\right) \nonumber\\ & \le \frac{1}{\lambda} \frac{\alpha_1^{q-1}}{\alpha_2^{q-1}}\cdot \frac{\ln_q (\alpha_1^{{-}1})}{\ln_q (\alpha_2^{{-}1})} \alpha_2^{q-1}\ln_q \mathbb{E}[\exp_q(\lambda X)] + \frac{1}{\lambda} \frac{\alpha_1^{q-1}}{\alpha_2^{q-1}}\cdot \frac{\ln_q (\alpha_1^{{-}1})}{\ln_q (\alpha_2^{{-}1})} \ln_q \left(\frac{1}{\alpha_2}\right) \nonumber\\ & = \frac{\alpha_1^{q-1}}{\alpha_2^{q-1}} \frac{\ln_q (\alpha_1^{{-}1})}{\ln_q (\alpha_2^{{-}1})}\cdot \frac{1}{\lambda}\ln_q \left(\frac{1}{\alpha_2} \mathbb{E}[\exp_q(\lambda X)]\right) \nonumber\\ & = \frac{\ln_q (\alpha_1^2) - \ln_q (\alpha_1)}{\ln_q (\alpha_2^2) - \ln_q (\alpha_2)} \cdot \frac{1}{\lambda}\ln_q \left( \frac{1}{\alpha_2} \mathbb{E}[\exp_q(\lambda X)]\right), \end{align}
\begin{align} \frac{1}{\lambda}\ln_q \left[\frac{1}{\alpha_1} \mathbb{E}[\exp_q(\lambda X)]\right] & = \frac{1}{\lambda}\alpha_1^{q-1}\ln_q \mathbb{E}[\exp_q(\lambda X)] + \frac{1}{\lambda}\ln_q \left(\frac{1}{\alpha_1}\right) \nonumber\\ & = \frac{1}{\lambda}\frac{\alpha_1^{q-1}}{\alpha_2^{q-1}} \alpha_2^{q-1}\ln_q \mathbb{E}[\exp_q(\lambda X)] + \frac{1}{\lambda}\frac{\ln_q (\alpha_1^{{-}1})}{\ln_q (\alpha_2^{{-}1})} \ln_q \left(\frac{1}{\alpha_2}\right) \nonumber\\ & \le \frac{1}{\lambda} \frac{\alpha_1^{q-1}}{\alpha_2^{q-1}}\cdot \frac{\ln_q (\alpha_1^{{-}1})}{\ln_q (\alpha_2^{{-}1})} \alpha_2^{q-1}\ln_q \mathbb{E}[\exp_q(\lambda X)] + \frac{1}{\lambda} \frac{\alpha_1^{q-1}}{\alpha_2^{q-1}}\cdot \frac{\ln_q (\alpha_1^{{-}1})}{\ln_q (\alpha_2^{{-}1})} \ln_q \left(\frac{1}{\alpha_2}\right) \nonumber\\ & = \frac{\alpha_1^{q-1}}{\alpha_2^{q-1}} \frac{\ln_q (\alpha_1^{{-}1})}{\ln_q (\alpha_2^{{-}1})}\cdot \frac{1}{\lambda}\ln_q \left(\frac{1}{\alpha_2} \mathbb{E}[\exp_q(\lambda X)]\right) \nonumber\\ & = \frac{\ln_q (\alpha_1^2) - \ln_q (\alpha_1)}{\ln_q (\alpha_2^2) - \ln_q (\alpha_2)} \cdot \frac{1}{\lambda}\ln_q \left( \frac{1}{\alpha_2} \mathbb{E}[\exp_q(\lambda X)]\right), \end{align}
where the last equality follows since
 \begin{align*} \frac{\alpha_1^{q-1}}{\alpha_2^{q-1}}\frac{\ln_q (\alpha_1^{{-}1})}{\ln_q (\alpha_2^{{-}1})} & = \frac{\alpha_1^{q-1} (\alpha_1^{q-1}-1)/(1-q)}{\alpha_2^{q-1} (\alpha_2^{q-1}-1)/(1-q)} \\ & =\frac{(\alpha_1^{2(q-1)}-1)- (\alpha_1^{q-1}-1)}{(\alpha_2^{2(q-1)}-1)- (\alpha_2^{q-1}-1)} = \frac{\ln_q (\alpha_1^2) - \ln_q (\alpha_1)}{\ln_q (\alpha_2^2) - \ln_q (\alpha_2)}. \end{align*}
\begin{align*} \frac{\alpha_1^{q-1}}{\alpha_2^{q-1}}\frac{\ln_q (\alpha_1^{{-}1})}{\ln_q (\alpha_2^{{-}1})} & = \frac{\alpha_1^{q-1} (\alpha_1^{q-1}-1)/(1-q)}{\alpha_2^{q-1} (\alpha_2^{q-1}-1)/(1-q)} \\ & =\frac{(\alpha_1^{2(q-1)}-1)- (\alpha_1^{q-1}-1)}{(\alpha_2^{2(q-1)}-1)- (\alpha_2^{q-1}-1)} = \frac{\ln_q (\alpha_1^2) - \ln_q (\alpha_1)}{\ln_q (\alpha_2^2) - \ln_q (\alpha_2)}. \end{align*}
By taking the infimum over all ![]() $\lambda \gt 0$ in the both sides of (3.9), we conclude that
$\lambda \gt 0$ in the both sides of (3.9), we conclude that
This completes the proof of the proposition.
Next, we establish the strong monotonicity of ![]() $\mathrm {TsVaR}$. Ahmadi-Javid and Fallah-Tafti [Reference Ahmadi-Javid and Fallah-Tafti3] showed that EVaR also possesses this property, which does not hold for other popular (coherent or non-coherent) monotone risk measures such as the VaR or Expected Shortfall. Recall the definition of strongly monotonicity.
$\mathrm {TsVaR}$. Ahmadi-Javid and Fallah-Tafti [Reference Ahmadi-Javid and Fallah-Tafti3] showed that EVaR also possesses this property, which does not hold for other popular (coherent or non-coherent) monotone risk measures such as the VaR or Expected Shortfall. Recall the definition of strongly monotonicity.
Definition 3.2. A risk measure ![]() $\rho$ is called strongly monotone if it holds that
$\rho$ is called strongly monotone if it holds that ![]() $\rho (X) \gt \rho (Y)$ for any pair of random variables
$\rho (X) \gt \rho (Y)$ for any pair of random variables ![]() $X$ and
$X$ and ![]() $Y$ in the domain of
$Y$ in the domain of ![]() $\rho$ that satisfy the conditions
$\rho$ that satisfy the conditions
(C1)
 $X \ge Y$ and
$X \ge Y$ and  $\mathbb {P}(X \gt Y) \gt 0$.
$\mathbb {P}(X \gt Y) \gt 0$.(C2)
 $\text {ess-sup} (X) \gt \text {ess-sup} (Y)$ or
$\text {ess-sup} (X) \gt \text {ess-sup} (Y)$ or  $\text {ess-sup} (X) =\text {ess-sup} (Y)=+\infty$.
$\text {ess-sup} (X) =\text {ess-sup} (Y)=+\infty$.
Theorem 3.12. (Strong monotonicity of  $\mathrm {TsVaR}$)
$\mathrm {TsVaR}$)
Let ![]() $X$ and
$X$ and ![]() $Y$ be random variables in the space
$Y$ be random variables in the space ![]() $E''$ that satisfy Conditions (C1) and (C2). Then,
$E''$ that satisfy Conditions (C1) and (C2). Then,
Proof. From (3.1) and Proposition 2.1, we have
Since ![]() $\exp _q(\cdot )$ is strictly increasing, Condition (C1) ensures that
$\exp _q(\cdot )$ is strictly increasing, Condition (C1) ensures that ![]() $\mathbb {E}[\exp _q(\lambda X)] \gt \mathbb {E}[\exp _q(\lambda X)]$ for
$\mathbb {E}[\exp _q(\lambda X)] \gt \mathbb {E}[\exp _q(\lambda X)]$ for ![]() $\lambda \gt 0$. Thus,
$\lambda \gt 0$. Thus,
 \begin{align*} t_X(\alpha, \lambda) & = \frac{1}{\lambda} \alpha^{q-1} \ln_q (\mathbb{E}[\exp_q(\lambda X)]) + \frac{1}{\lambda} \ln_q \left(\frac{1}{\alpha}\right) \\ & \gt \frac{1}{\lambda} \alpha^{q-1} \ln_q (\mathbb{E}[\exp_q(\lambda Y) ]) + \frac{1}{\lambda} \ln_q \left(\frac{1}{\alpha}\right) = t_Y(\alpha, \lambda) \end{align*}
\begin{align*} t_X(\alpha, \lambda) & = \frac{1}{\lambda} \alpha^{q-1} \ln_q (\mathbb{E}[\exp_q(\lambda X)]) + \frac{1}{\lambda} \ln_q \left(\frac{1}{\alpha}\right) \\ & \gt \frac{1}{\lambda} \alpha^{q-1} \ln_q (\mathbb{E}[\exp_q(\lambda Y) ]) + \frac{1}{\lambda} \ln_q \left(\frac{1}{\alpha}\right) = t_Y(\alpha, \lambda) \end{align*}
since ![]() $\ln _q(\cdot )$ is strictly increasing. Moreover, by Condition (C2), we have
$\ln _q(\cdot )$ is strictly increasing. Moreover, by Condition (C2), we have
or
Note that ![]() $t_X(\alpha, \lambda )$ is continuous in
$t_X(\alpha, \lambda )$ is continuous in ![]() $\lambda \gt 0$. Therefore,
$\lambda \gt 0$. Therefore,
This ends the proof.
In the end of this section, we give an example to compare the EVaR and TsVaR for a random variable with ![]() $U(0,1)$ distribution.
$U(0,1)$ distribution.
Example 3.13. For ![]() $X \sim U(0,1)$ and
$X \sim U(0,1)$ and ![]() $q\in (0,1)$, it follows from (3.1) and (3.3) that
$q\in (0,1)$, it follows from (3.1) and (3.3) that
 \begin{align*} & \mathrm{TsVaR}_{1-\alpha}(X) = \inf_{\lambda \gt 0} \left\{ \frac{1}{\lambda} \ln_q \left( \frac{(1+(1-q)\lambda)^{(2-q)/(1-q)} -1}{\alpha \lambda (2-q)} \right) \right\},\\ & \mathrm{EVaR}_{1-\alpha}(X) =\inf_{\lambda \gt 0}\left\{\lambda\ln \left(\lambda \exp\left( \frac{1}{\lambda}\right)-\lambda\right)-\lambda\ln\alpha \right\}, \quad \alpha\in (0,1). \end{align*}
\begin{align*} & \mathrm{TsVaR}_{1-\alpha}(X) = \inf_{\lambda \gt 0} \left\{ \frac{1}{\lambda} \ln_q \left( \frac{(1+(1-q)\lambda)^{(2-q)/(1-q)} -1}{\alpha \lambda (2-q)} \right) \right\},\\ & \mathrm{EVaR}_{1-\alpha}(X) =\inf_{\lambda \gt 0}\left\{\lambda\ln \left(\lambda \exp\left( \frac{1}{\lambda}\right)-\lambda\right)-\lambda\ln\alpha \right\}, \quad \alpha\in (0,1). \end{align*}
Figure 1 plots ![]() $\mathrm {EVaR}_{1-\alpha }(X)$ and
$\mathrm {EVaR}_{1-\alpha }(X)$ and ![]() $\mathrm {TsVaR}_{1-\alpha }(X)$ with respect to different
$\mathrm {TsVaR}_{1-\alpha }(X)$ with respect to different ![]() $\alpha$ with
$\alpha$ with ![]() $q=0.4, 0.8$ and
$q=0.4, 0.8$ and ![]() $1$. We observe that the premium principle calculating via TsVaR is conservative when considering small
$1$. We observe that the premium principle calculating via TsVaR is conservative when considering small ![]() $\alpha$, and that as
$\alpha$, and that as ![]() $q \nearrow 1$, TsVaR converges to EVaR, which is consistent with our conclusion. The advantage of TsVaR is that the size of
$q \nearrow 1$, TsVaR converges to EVaR, which is consistent with our conclusion. The advantage of TsVaR is that the size of ![]() $q$ can be determined according to the current state, which coincided with the idea of Tsallis [Reference Tsallis25], that is, the parameter
$q$ can be determined according to the current state, which coincided with the idea of Tsallis [Reference Tsallis25], that is, the parameter ![]() $q$ in Tsallis relative entropy can be viewed as a bias of the original probability measure. If the insurer believes that the insurable loss
$q$ in Tsallis relative entropy can be viewed as a bias of the original probability measure. If the insurer believes that the insurable loss ![]() $X$ has potential huge loss or uncertainty about the distribution of
$X$ has potential huge loss or uncertainty about the distribution of ![]() $X$, the insurer can choose smaller
$X$, the insurer can choose smaller ![]() $q$ and
$q$ and ![]() $\alpha$ to ensure its own safety.
$\alpha$ to ensure its own safety.

Figure 1. ![]() $\mathrm {EVaR}_{1-\alpha }$ and
$\mathrm {EVaR}_{1-\alpha }$ and ![]() $\mathrm {TsVaR}_{1-\alpha }$ for a random variable
$\mathrm {TsVaR}_{1-\alpha }$ for a random variable ![]() $X\sim U(0,1)$ with
$X\sim U(0,1)$ with ![]() $q=0.4, 0.8$, and
$q=0.4, 0.8$, and ![]() $1$.
$1$.
4. Banach spaces
Given a coherent risk measure ![]() $\rho$, one may define the semi-norm
$\rho$, one may define the semi-norm ![]() $\|\cdot \|_{\rho }:= \rho (|\cdot |)$ on the same model space (see [Reference Pichler17]). It is well known that risk functional
$\|\cdot \|_{\rho }:= \rho (|\cdot |)$ on the same model space (see [Reference Pichler17]). It is well known that risk functional ![]() $\rho$ is Lipschitz continuous with respect to the associated norm
$\rho$ is Lipschitz continuous with respect to the associated norm ![]() $\|\cdot \|_{\rho }$ . In this section, we consider the
$\|\cdot \|_{\rho }$ . In this section, we consider the ![]() $\mathrm {TsVaR}$ norm, which is generated by
$\mathrm {TsVaR}$ norm, which is generated by ![]() $\mathrm {TsVaR}$ as follows,
$\mathrm {TsVaR}$ as follows, ![]() $\|\cdot \|= \mathrm {TsVaR}_{\alpha } (|\cdot |)$. Recall that we consider the nonnegative random variables. Then, the norm can simplify to
$\|\cdot \|= \mathrm {TsVaR}_{\alpha } (|\cdot |)$. Recall that we consider the nonnegative random variables. Then, the norm can simplify to ![]() $\|\cdot \|= \mathrm {TsVaR}_{\alpha }(\cdot )$. We first show both
$\|\cdot \|= \mathrm {TsVaR}_{\alpha }(\cdot )$. We first show both ![]() $E$ and
$E$ and ![]() $E''$ equipped with
$E''$ equipped with ![]() $\mathrm {TsVaR}$ norm
$\mathrm {TsVaR}$ norm ![]() $\|\cdot \|$ are Banach spaces.
$\|\cdot \|$ are Banach spaces.
Theorem 4.1. For ![]() $0 \lt q\le 1$ and
$0 \lt q\le 1$ and ![]() $0 \lt \alpha \lt 1$, denote
$0 \lt \alpha \lt 1$, denote ![]() $\|\cdot \|:= \mathrm {TsVaR}_{\alpha }(\cdot )$. Then, the pairs
$\|\cdot \|:= \mathrm {TsVaR}_{\alpha }(\cdot )$. Then, the pairs
are (different) Banach spaces.
Proof. First, we prove that ![]() $\|\cdot \|$ induced by
$\|\cdot \|$ induced by ![]() $\mathrm {TsVaR}_\alpha$ is a norm. Since
$\mathrm {TsVaR}_\alpha$ is a norm. Since ![]() $\|\cdot \|$ is a semi-norm, it suffices to prove that
$\|\cdot \|$ is a semi-norm, it suffices to prove that ![]() $\|X\|=0$ for
$\|X\|=0$ for ![]() $X\in E''$ implies
$X\in E''$ implies ![]() $X=0$, a.s. Assume
$X=0$, a.s. Assume ![]() $\mathrm {TsVaR}_{\alpha }(X)=0$. From (3.2), it follows that
$\mathrm {TsVaR}_{\alpha }(X)=0$. From (3.2), it follows that ![]() $\mathbb {E} [X]=0$, implying
$\mathbb {E} [X]=0$, implying ![]() $X=0$ almost sure. Thus,
$X=0$ almost sure. Thus, ![]() $\|\cdot \|$ is a normal.
$\|\cdot \|$ is a normal.
Next, we show that ![]() $E$ and
$E$ and ![]() $E''$ are complete under the normal
$E''$ are complete under the normal ![]() $\|\cdot \|$. Assume that
$\|\cdot \|$. Assume that ![]() $0 \lt q \lt 1$ since the case of
$0 \lt q \lt 1$ since the case of ![]() $q=1$ reduces to Theorem 2.14 in Ahmadi-Javid and Pichler [Reference Ahmadi-Javid and Pichler4]. We only consider the space
$q=1$ reduces to Theorem 2.14 in Ahmadi-Javid and Pichler [Reference Ahmadi-Javid and Pichler4]. We only consider the space ![]() $E''$ since
$E''$ since ![]() $E=E''$ when
$E=E''$ when ![]() $0 \lt q \lt 1$. Let
$0 \lt q \lt 1$. Let ![]() $\{X_n\}$ be a Cauchy sequence in
$\{X_n\}$ be a Cauchy sequence in ![]() $E''$. For
$E''$. For ![]() $\epsilon \gt 0$, there exists
$\epsilon \gt 0$, there exists ![]() $n_0 \gt 0$ such that
$n_0 \gt 0$ such that ![]() $\|X_n-X_m\| \lt \epsilon$ whenever
$\|X_n-X_m\| \lt \epsilon$ whenever ![]() $m, n \gt n_0$, and thus
$m, n \gt n_0$, and thus ![]() $|\|X_m\|-\|X_n\| | \le \|X_n-X_m\| \lt \epsilon$. Thus,
$|\|X_m\|-\|X_n\| | \le \|X_n-X_m\| \lt \epsilon$. Thus, ![]() $\lim _{n \to \infty }\|X_n\|$ exists and is finite, and
$\lim _{n \to \infty }\|X_n\|$ exists and is finite, and ![]() $\|X_n\| \lt C$ for all
$\|X_n\| \lt C$ for all ![]() $n\ge 1$.
$n\ge 1$.
Now recall that ![]() $\|X_n\| =\mathrm {TsVaR}_\alpha (X_n)$, so there exists
$\|X_n\| =\mathrm {TsVaR}_\alpha (X_n)$, so there exists ![]() $\lambda _n \gt 0$ in (3.1) such that
$\lambda _n \gt 0$ in (3.1) such that
Since ![]() $\mathbb {E}[\exp _q(\lambda _n X_n)] \ge 1$, we have
$\mathbb {E}[\exp _q(\lambda _n X_n)] \ge 1$, we have
It follows that
and ![]() $\mathbb {E} [\exp _q(\lambda X_n)]$ is well-defined by (4.1) for every
$\mathbb {E} [\exp _q(\lambda X_n)]$ is well-defined by (4.1) for every ![]() $\lambda \lt \lambda ^\ast$. Recall from Remark 3.1 that
$\lambda \lt \lambda ^\ast$. Recall from Remark 3.1 that ![]() $(1-\alpha )^{q-1} \mathbb {E}(X) \le \mathrm {TsVaR}_{\alpha }(X)$. Thus,
$(1-\alpha )^{q-1} \mathbb {E}(X) \le \mathrm {TsVaR}_{\alpha }(X)$. Thus, ![]() $\{X_n\}$ is a Cauchy sequence for
$\{X_n\}$ is a Cauchy sequence for ![]() $L^1$ as well, which implies that there exists
$L^1$ as well, which implies that there exists ![]() $X\in L^1$ such that
$X\in L^1$ such that ![]() $X_n\stackrel {L_1}{\longrightarrow } X$. It remains to show that
$X_n\stackrel {L_1}{\longrightarrow } X$. It remains to show that ![]() $X \in E''$ and that
$X \in E''$ and that ![]() $\mathrm {TsVaR}_\alpha (|X - X_n|)\to 0$ as
$\mathrm {TsVaR}_\alpha (|X - X_n|)\to 0$ as ![]() $n\to \infty$.
$n\to \infty$.
• We prove
 $X\in E''$. If there exists a subsequence
$X\in E''$. If there exists a subsequence  $\{n_k\}$ such that
$\{n_k\}$ such that  $\lambda _{n_k}\to \lambda ^\ast$, from (4.1), it follows that
Thus, by Fatou's lemma, we have
$\lambda _{n_k}\to \lambda ^\ast$, from (4.1), it follows that
Thus, by Fatou's lemma, we have $$\liminf_{k\to\infty} \mathbb{E}[\exp_q(\lambda_{n_k} X_{n_k})] \le (1-\alpha) \exp_q(\lambda^\ast C).$$
implying
$$\liminf_{k\to\infty} \mathbb{E}[\exp_q(\lambda_{n_k} X_{n_k})] \le (1-\alpha) \exp_q(\lambda^\ast C).$$
implying $$\mathbb{E}[\exp_q(\lambda^\ast X) ] \le \liminf_{k \to \infty} \mathbb{E}[\exp_q(\lambda^\ast X_{n_k}) ] \le \liminf_{k \to \infty} \mathbb{E}[\exp_q(\lambda_{n_k} X_{n_k})] \le (1-\alpha) \exp_q(\lambda^* C) \lt \infty,$$
$$\mathbb{E}[\exp_q(\lambda^\ast X) ] \le \liminf_{k \to \infty} \mathbb{E}[\exp_q(\lambda^\ast X_{n_k}) ] \le \liminf_{k \to \infty} \mathbb{E}[\exp_q(\lambda_{n_k} X_{n_k})] \le (1-\alpha) \exp_q(\lambda^* C) \lt \infty,$$
 $X\in E''$. If
$X\in E''$. If  $\liminf _{n\to \infty } \lambda _n \gt \lambda ^\ast$, then there exists a subsequence
$\liminf _{n\to \infty } \lambda _n \gt \lambda ^\ast$, then there exists a subsequence  $\{n_k\}$ such that
$\{n_k\}$ such that  $\lambda _{n_k} \gt \lambda ^\ast$ for any
$\lambda _{n_k} \gt \lambda ^\ast$ for any  $k\ge 1$. Thus, by Lemma 3.2 and (4.1),
implying that
$k\ge 1$. Thus, by Lemma 3.2 and (4.1),
implying that \begin{align*} \frac{1}{\lambda^\ast} \ln_q (\mathbb{E}[\exp_q (\lambda^\ast X_{n_k}) ] ) & = \frac{1}{\lambda^\ast} \ln_q \left ( \mathbb{E} \left [\exp_q \left( \frac{\lambda^\ast}{\lambda_{n_k}} \cdot \lambda_{n_k} X_{n_k} + \left(1-\frac{\lambda^\ast}{\lambda_{n_k}}\right) \cdot 0\right) \right ] \right ) \\ & \le \frac{1}{\lambda_{n_k}} \ln_q ( \mathbb{E} [\exp_q (\lambda_{n_k} X_{n_k}) ] ) \\ & \le \frac{1}{\lambda_{n_k}} \ln_q \left (\frac{1}{1-\alpha} \mathbb{E} [\exp_q(\lambda_{n_k} X_{n_k})]\right ) \lt C, \end{align*}
\begin{align*} \frac{1}{\lambda^\ast} \ln_q (\mathbb{E}[\exp_q (\lambda^\ast X_{n_k}) ] ) & = \frac{1}{\lambda^\ast} \ln_q \left ( \mathbb{E} \left [\exp_q \left( \frac{\lambda^\ast}{\lambda_{n_k}} \cdot \lambda_{n_k} X_{n_k} + \left(1-\frac{\lambda^\ast}{\lambda_{n_k}}\right) \cdot 0\right) \right ] \right ) \\ & \le \frac{1}{\lambda_{n_k}} \ln_q ( \mathbb{E} [\exp_q (\lambda_{n_k} X_{n_k}) ] ) \\ & \le \frac{1}{\lambda_{n_k}} \ln_q \left (\frac{1}{1-\alpha} \mathbb{E} [\exp_q(\lambda_{n_k} X_{n_k})]\right ) \lt C, \end{align*}
 $\mathbb {E}[\exp _q (\lambda ^\ast X_{n_k}) ] \lt \exp _q(\lambda ^\ast C)$. Again, applying Fatou's lemma, we have
implying
$\mathbb {E}[\exp _q (\lambda ^\ast X_{n_k}) ] \lt \exp _q(\lambda ^\ast C)$. Again, applying Fatou's lemma, we have
implying $$\mathbb{E}[\exp_q(\lambda^\ast X) ] \le \liminf_{k \to \infty} \mathbb{E}[\exp_q(\lambda^\ast X_{n_k}) ] \le \exp_q(\lambda^* C) \lt \infty,$$
$$\mathbb{E}[\exp_q(\lambda^\ast X) ] \le \liminf_{k \to \infty} \mathbb{E}[\exp_q(\lambda^\ast X_{n_k}) ] \le \exp_q(\lambda^* C) \lt \infty,$$
 $X\in E''$.
$X\in E''$.• We prove that
 $\mathrm {TsVaR}_\alpha (|X-X_n|)\to 0$. For
$\mathrm {TsVaR}_\alpha (|X-X_n|)\to 0$. For  $\epsilon \gt 0$, choose
$\epsilon \gt 0$, choose  $n_0 \gt 0$ such that
$n_0 \gt 0$ such that  $\mathrm {TsVaR}_\alpha (|X_n-X_m|) \lt \epsilon$ for
$\mathrm {TsVaR}_\alpha (|X_n-X_m|) \lt \epsilon$ for  $m, n \gt n_0$. Therefore, there exists
$m, n \gt n_0$. Therefore, there exists  $\lambda _{n,m} \gt 0$ such that
implying that
$\lambda _{n,m} \gt 0$ such that
implying that $$\frac{1}{\lambda_{n,m}} \ln_q \left(\frac{1}{1-\alpha}\right) \le \frac{1}{\lambda_{n,m}} \ln_q \left(\frac{1}{1-\alpha} \mathbb{E}[\exp_q(\lambda_{n,m} |X_n-X_m|)]\right) \lt \epsilon,$$
$$\frac{1}{\lambda_{n,m}} \ln_q \left(\frac{1}{1-\alpha}\right) \le \frac{1}{\lambda_{n,m}} \ln_q \left(\frac{1}{1-\alpha} \mathbb{E}[\exp_q(\lambda_{n,m} |X_n-X_m|)]\right) \lt \epsilon,$$
 $\lambda _{n,m} \gt \lambda _1^* := \epsilon ^{-1} \ln _q ({1}/{(1-\alpha )})$. Again, by Lemma 3.2, we have
Applying Fatou's lemma, we have
$\lambda _{n,m} \gt \lambda _1^* := \epsilon ^{-1} \ln _q ({1}/{(1-\alpha )})$. Again, by Lemma 3.2, we have
Applying Fatou's lemma, we have \begin{align*} \frac{1}{\lambda_1^\ast} \ln_q( \mathbb{E}[\exp_q (\lambda_1^\ast |X_n-X_m|)]) & = \frac{1}{\lambda_1^\ast} \ln_q \left(\mathbb{E}\left [\exp_q \left(\frac{\lambda_1^\ast}{\lambda_{n,m}} \cdot \lambda_{n,m} |X_n-X_m|\right) \right ]\right) \\ & \le \frac{1}{\lambda_{n,m}} \ln_q(\mathbb{E}[\exp_q(\lambda_{n,m} |X_n-X_m|)])\\ & \le \frac{1}{\lambda_{n,m}} \ln_q \left[\frac{1}{1-\alpha} \mathbb{E}[\exp_q(\lambda_{n,m} |X_n-X_m|)]\right] \lt \epsilon. \end{align*}
Hence,
\begin{align*} \frac{1}{\lambda_1^\ast} \ln_q( \mathbb{E}[\exp_q (\lambda_1^\ast |X_n-X_m|)]) & = \frac{1}{\lambda_1^\ast} \ln_q \left(\mathbb{E}\left [\exp_q \left(\frac{\lambda_1^\ast}{\lambda_{n,m}} \cdot \lambda_{n,m} |X_n-X_m|\right) \right ]\right) \\ & \le \frac{1}{\lambda_{n,m}} \ln_q(\mathbb{E}[\exp_q(\lambda_{n,m} |X_n-X_m|)])\\ & \le \frac{1}{\lambda_{n,m}} \ln_q \left[\frac{1}{1-\alpha} \mathbb{E}[\exp_q(\lambda_{n,m} |X_n-X_m|)]\right] \lt \epsilon. \end{align*}
Hence, $$\mathbb{E}[\exp_q(\lambda_1^\ast |X-X_m|)] \le \liminf_{n\to\infty} \mathbb{E}[\exp_q(\lambda_1^\ast |X_n-X_m|)] \lt \exp_q(\lambda_1^\ast \epsilon).$$
Since
$$\mathbb{E}[\exp_q(\lambda_1^\ast |X-X_m|)] \le \liminf_{n\to\infty} \mathbb{E}[\exp_q(\lambda_1^\ast |X_n-X_m|)] \lt \exp_q(\lambda_1^\ast \epsilon).$$
Since \begin{align*} & \frac{1}{\lambda_1^\ast} \ln_q \left(\frac{1}{1-\alpha} \mathbb{E}[\exp_q(\lambda_1^\ast |X-X_m|) ]\right) \\ & \quad = \frac{1}{\lambda_1^\ast} (1-\alpha)^{q-1} \ln_q \mathbb{E}[\exp_q(\lambda_1^\ast |X-X_m|) ] + \frac{1}{\lambda_1^\ast} \ln_q \left(\frac{1}{1-\alpha}\right) \\ & \quad \le (1-\alpha)^{q-1} \epsilon + \epsilon. \end{align*}
\begin{align*} & \frac{1}{\lambda_1^\ast} \ln_q \left(\frac{1}{1-\alpha} \mathbb{E}[\exp_q(\lambda_1^\ast |X-X_m|) ]\right) \\ & \quad = \frac{1}{\lambda_1^\ast} (1-\alpha)^{q-1} \ln_q \mathbb{E}[\exp_q(\lambda_1^\ast |X-X_m|) ] + \frac{1}{\lambda_1^\ast} \ln_q \left(\frac{1}{1-\alpha}\right) \\ & \quad \le (1-\alpha)^{q-1} \epsilon + \epsilon. \end{align*}
 $\epsilon$ is arbitrary, it follows that
$\epsilon$ is arbitrary, it follows that  $\mathrm {TsVaR}_\alpha (|X_n-X|)\to 0$. Thus,
$\mathrm {TsVaR}_\alpha (|X_n-X|)\to 0$. Thus,  $E''$ is complete.
$E''$ is complete.
This completes the proof of the theorem.
In the next theorem, we proceed with a comparison of the ![]() $\mathrm {TsVaR}$ norm with the
$\mathrm {TsVaR}$ norm with the ![]() $L^p$-norms
$L^p$-norms ![]() $\|\cdot \|_p$.
$\|\cdot \|_p$.
Theorem 4.2. For ![]() $0 \lt q\le 1$ and
$0 \lt q\le 1$ and ![]() $0 \lt \alpha \lt 1$, denote
$0 \lt \alpha \lt 1$, denote ![]() $\|\cdot \|=\mathrm {TsVaR}_\alpha (\cdot )$. Then,
$\|\cdot \|=\mathrm {TsVaR}_\alpha (\cdot )$. Then,
and
Furthermore, for every ![]() $1 \lt p \lt \kappa _q$, there exists a finite constant
$1 \lt p \lt \kappa _q$, there exists a finite constant ![]() $c_{p,q}$ such that
$c_{p,q}$ such that
where
and
with ![]() $\beta =1-\exp _q(1-p)$.
$\beta =1-\exp _q(1-p)$.
Proof. Note that (4.2) and (4.3) follow from (3.2), and that Theorem 3.1 in Ahmadi-Javid and Pichler [Reference Ahmadi-Javid and Pichler4] gives the proof for the case ![]() $q=1$.
$q=1$.
To prove (4.4), we assume ![]() $0 \lt q \lt 1$. For any fixed
$0 \lt q \lt 1$. For any fixed ![]() $p$ such that
$p$ such that ![]() $1 \lt p \lt \kappa _q$, it follows that
$1 \lt p \lt \kappa _q$, it follows that ![]() $1-p \gt 1-\kappa _q =-1/(1-q)$. Define
$1-p \gt 1-\kappa _q =-1/(1-q)$. Define ![]() $\beta =1-\exp _q(1-p)$ so that
$\beta =1-\exp _q(1-p)$ so that ![]() $\beta \in (0,1)$, and denote
$\beta \in (0,1)$, and denote ![]() $\phi (x) = (\ln _q(x))^p$. It can be checked that
$\phi (x) = (\ln _q(x))^p$. It can be checked that
which is negative and, hence, ![]() $\phi (x)$ is concave, when
$\phi (x)$ is concave, when ![]() $x\ge 1$. Since
$x\ge 1$. Since ![]() $\exp _q(\lambda X)/\exp _q(1-p) \ge 1$, by Jensen's inequality, we have
$\exp _q(\lambda X)/\exp _q(1-p) \ge 1$, by Jensen's inequality, we have
 \begin{align} \frac{1}{\lambda} \ln_q \left (\frac{1}{1-\beta} \mathbb{E}[\exp_q(\lambda X)]\right ) & =\frac{1}{\lambda} \left(\phi \left[ \frac{1}{1-\beta} \mathbb{E}[\exp_q(\lambda X)]\right] \right)^{1/p}\nonumber\\ & \ge\frac{1}{\lambda} \left [\mathbb{E} \circ \phi \left(\frac{\exp_q(\lambda X)}{1-\beta} \right) \right ]^{1/p} \nonumber\\ & = \frac{1}{\lambda} \left(\mathbb{E} \left[ (1-\beta)^{q-1} \lambda X + \ln_q \left(\frac{1}{1-\beta}\right) \right]^p \right)^{1/p} \nonumber\\ & \ge \frac{1}{\lambda} (\mathbb{E}[ (1-\beta)^{q-1} \lambda X ]^p )^{1/p} = (1-\beta)^{q-1} \|X\|_p. \end{align}
\begin{align} \frac{1}{\lambda} \ln_q \left (\frac{1}{1-\beta} \mathbb{E}[\exp_q(\lambda X)]\right ) & =\frac{1}{\lambda} \left(\phi \left[ \frac{1}{1-\beta} \mathbb{E}[\exp_q(\lambda X)]\right] \right)^{1/p}\nonumber\\ & \ge\frac{1}{\lambda} \left [\mathbb{E} \circ \phi \left(\frac{\exp_q(\lambda X)}{1-\beta} \right) \right ]^{1/p} \nonumber\\ & = \frac{1}{\lambda} \left(\mathbb{E} \left[ (1-\beta)^{q-1} \lambda X + \ln_q \left(\frac{1}{1-\beta}\right) \right]^p \right)^{1/p} \nonumber\\ & \ge \frac{1}{\lambda} (\mathbb{E}[ (1-\beta)^{q-1} \lambda X ]^p )^{1/p} = (1-\beta)^{q-1} \|X\|_p. \end{align}
Taking the infimum in (4.5) among all ![]() $\lambda \gt 0$ yields that
$\lambda \gt 0$ yields that
Therefore, the desired result (4.4) follows from Proposition 3.11 immediately.
4.1. Relation to Orlicz spaces
In this subsection, we discuss the relationship between the Tsallis spaces and their equivalent Orlicz hearts and Orlicz spaces. Let ![]() $\Phi : [0, +\infty ) \to [0, +\infty )$ be convex with
$\Phi : [0, +\infty ) \to [0, +\infty )$ be convex with ![]() $\Phi (0)=0$,
$\Phi (0)=0$, ![]() $\Phi (1)=1$ and
$\Phi (1)=1$ and ![]() $\lim _{x\to \infty } \Phi (x)=\infty$. The convex conjugate of
$\lim _{x\to \infty } \Phi (x)=\infty$. The convex conjugate of ![]() $\Phi$ is defined as
$\Phi$ is defined as
These functions are called a pair of complementary Young functions in the context of Orlicz spaces with
Definition 4.1. For a pair ![]() $\Phi$ and
$\Phi$ and ![]() $\Psi$ of complementary Young functions, define the spaces
$\Psi$ of complementary Young functions, define the spaces
 \begin{align*} & L^{\Phi} = \{X \in L_+^0:\ \mathbb{E} [\Phi(c X)] \lt \infty \text{ for some } c \gt 0\}, \\ & M^{\Phi} = \{X \in L^0_+:\ \mathbb{E} [\Phi(c X)] \lt \infty \text{ for all } c \gt 0\}, \end{align*}
\begin{align*} & L^{\Phi} = \{X \in L_+^0:\ \mathbb{E} [\Phi(c X)] \lt \infty \text{ for some } c \gt 0\}, \\ & M^{\Phi} = \{X \in L^0_+:\ \mathbb{E} [\Phi(c X)] \lt \infty \text{ for all } c \gt 0\}, \end{align*}
and the norms
 \begin{align*} & \| X\|_{\Phi} = \inf\left\{\lambda \gt 0:\ \mathbb{E} \left[ \Phi\left( \left| \frac{X}{\lambda} \right| \right) \right] \le 1\right\}, \\ & \| X\|^\ast_{\Phi} = \sup_{\mathbb{E} [\Psi(|Y|)] \le 1} \mathbb{E} [XY] = \inf_{t \gt 0}\left\{\frac{1}{t} (1 + \mathbb{E} [\Phi(t |X|)])\right\}. \end{align*}
\begin{align*} & \| X\|_{\Phi} = \inf\left\{\lambda \gt 0:\ \mathbb{E} \left[ \Phi\left( \left| \frac{X}{\lambda} \right| \right) \right] \le 1\right\}, \\ & \| X\|^\ast_{\Phi} = \sup_{\mathbb{E} [\Psi(|Y|)] \le 1} \mathbb{E} [XY] = \inf_{t \gt 0}\left\{\frac{1}{t} (1 + \mathbb{E} [\Phi(t |X|)])\right\}. \end{align*}
The norms ![]() $\|X\|_{\Phi }$ and
$\|X\|_{\Phi }$ and ![]() $\|X\|^\ast _{\Phi }$ are called the Luxemburg norm and Orlicz norm, respectively. The spaces
$\|X\|^\ast _{\Phi }$ are called the Luxemburg norm and Orlicz norm, respectively. The spaces ![]() $L^{\Phi }$ and
$L^{\Phi }$ and ![]() $M^{\Phi }$ are called the Orlicz space and Orlicz heart, respectively. Similarly, define
$M^{\Phi }$ are called the Orlicz space and Orlicz heart, respectively. Similarly, define ![]() $L^{\Psi }$ and
$L^{\Psi }$ and ![]() $M^{\Psi }$ as well as the norms
$M^{\Psi }$ as well as the norms ![]() $\|X\|_{\Psi }$ and
$\|X\|_{\Psi }$ and ![]() $\|X\|^\ast _{\Psi }$.
$\|X\|^\ast _{\Psi }$.
In the rest of this paper, we assume ![]() $0 \lt q\le 1$ and consider the following pair of Young functions
$0 \lt q\le 1$ and consider the following pair of Young functions
and
Proposition 4.3. For ![]() $0 \lt q\le 1$, let
$0 \lt q\le 1$, let ![]() $\Phi$ and
$\Phi$ and ![]() $\Psi$ be a pair of Young functions defined by (4.6) and (4.7), respectively. Then
$\Psi$ be a pair of Young functions defined by (4.6) and (4.7), respectively. Then ![]() $E = M^{\Phi }$,
$E = M^{\Phi }$, ![]() $E'=M^{\Psi }\subset L^{\Psi }$, and
$E'=M^{\Psi }\subset L^{\Psi }$, and ![]() $E'' = L^{\Phi }$. Indeed, for
$E'' = L^{\Phi }$. Indeed, for ![]() $0 \lt \alpha \lt 1$, the norms
$0 \lt \alpha \lt 1$, the norms
are equivalent on ![]() $E''$. Particularly, we have
$E''$. Particularly, we have
where ![]() $c_q = \max \{\exp _q(1), -\ln _q(1-\alpha )\}$.
$c_q = \max \{\exp _q(1), -\ln _q(1-\alpha )\}$.
Proof. It is easy to show that, for ![]() $x \ge 0$,
$x \ge 0$,
where ![]() $c_q = \max \{\exp _q(1), -\ln _q(1-\alpha )\}$. Then, for
$c_q = \max \{\exp _q(1), -\ln _q(1-\alpha )\}$. Then, for ![]() $X\in L_+^0$,
$X\in L_+^0$,
 \begin{align*} \ln_q \left(\frac{1}{1-\alpha} \mathbb{E}[\exp_q(\lambda X)]\right) & = (1-\alpha)^{q-1} (\ln_q \mathbb{E}[\exp_q(\lambda X)] - \ln_q(1-\alpha) ) \\ & \le (1-\alpha)^{q-1} (\mathbb{E}[\exp_q(\lambda X)] - 1-\ln_q(1-\alpha)) \\ & \le c_q(1-\alpha)^{q-1}(1 + \mathbb{E} [\Phi (\lambda X)]). \end{align*}
\begin{align*} \ln_q \left(\frac{1}{1-\alpha} \mathbb{E}[\exp_q(\lambda X)]\right) & = (1-\alpha)^{q-1} (\ln_q \mathbb{E}[\exp_q(\lambda X)] - \ln_q(1-\alpha) ) \\ & \le (1-\alpha)^{q-1} (\mathbb{E}[\exp_q(\lambda X)] - 1-\ln_q(1-\alpha)) \\ & \le c_q(1-\alpha)^{q-1}(1 + \mathbb{E} [\Phi (\lambda X)]). \end{align*}
Thus, for ![]() $X \in L^\Phi$, we have
$X \in L^\Phi$, we have
This proves that ![]() $L^\Phi \subset E''$. To prove the converse inequality, let
$L^\Phi \subset E''$. To prove the converse inequality, let ![]() $X \in E''$, that is, there exists
$X \in E''$, that is, there exists ![]() $\lambda \gt 0$ such that
$\lambda \gt 0$ such that ![]() $\mathbb {E} [\exp _q(\lambda X)] \lt \infty$. Then
$\mathbb {E} [\exp _q(\lambda X)] \lt \infty$. Then ![]() $X \in L^\Phi$ since
$X \in L^\Phi$ since ![]() $\Phi (x)\le \exp _q(x)$. So we get
$\Phi (x)\le \exp _q(x)$. So we get ![]() $L^\Phi =E''$. Similarly,
$L^\Phi =E''$. Similarly, ![]() $E=M^\Phi$.
$E=M^\Phi$.
Now consider the identity map ![]() $A: (L^\Phi, \|\cdot \|^*_{\Phi }) \to (E'', \mathrm {TsVaR}_\alpha (\cdot )),$ which is bounded. By the above reasoning,
$A: (L^\Phi, \|\cdot \|^*_{\Phi }) \to (E'', \mathrm {TsVaR}_\alpha (\cdot )),$ which is bounded. By the above reasoning, ![]() $A$ is bijective. Since
$A$ is bijective. Since ![]() $(E'', \mathrm {TsVaR}_\alpha (\cdot ))$ is a Banach space by Theorem 4.1, it follows from the bounded inverse theorem (open mapping theorem, see [Reference Rudin21] Corollary 2.12) that the inverse
$(E'', \mathrm {TsVaR}_\alpha (\cdot ))$ is a Banach space by Theorem 4.1, it follows from the bounded inverse theorem (open mapping theorem, see [Reference Rudin21] Corollary 2.12) that the inverse ![]() $A^{-1}$ is continuous as well, that is, there is a constant
$A^{-1}$ is continuous as well, that is, there is a constant ![]() $c' \lt \infty$ such that
$c' \lt \infty$ such that
Therefore, ![]() $\|\cdot \|=\mathrm {TsVaR}_\alpha (\cdot )$ and
$\|\cdot \|=\mathrm {TsVaR}_\alpha (\cdot )$ and ![]() $\|\cdot \|^\ast _{\Phi }$ are equivalent on
$\|\cdot \|^\ast _{\Phi }$ are equivalent on ![]() $E''$.
$E''$.
Finally, note that ![]() $\Psi$ does not satisfy
$\Psi$ does not satisfy ![]() $(\Delta _2)$ condition, that is,
$(\Delta _2)$ condition, that is, ![]() $\Psi (2x)\le k\psi (x)$ for every
$\Psi (2x)\le k\psi (x)$ for every ![]() $k \gt 2$ whenever
$k \gt 2$ whenever ![]() $x$ is large enough. By Theorems 2.1.11 and 2.1.17 of Edgar et al. [Reference Edgar, Sucheston and Edgar9], we know
$x$ is large enough. By Theorems 2.1.11 and 2.1.17 of Edgar et al. [Reference Edgar, Sucheston and Edgar9], we know ![]() $M^{\Psi } \subset L^{\Psi }$. This completes the proof of the proposition.
$M^{\Psi } \subset L^{\Psi }$. This completes the proof of the proposition.
4.2. Characterization of the dual norm
In this subsection, we consider the associated dual norm of ![]() $\mathrm {TsVaR}_\alpha$:
$\mathrm {TsVaR}_\alpha$:
Theorem 4.4. For ![]() $0 \lt q\le 1$ and
$0 \lt q\le 1$ and ![]() $0 \lt \alpha \lt 1$, we have
$0 \lt \alpha \lt 1$, we have
 \begin{equation} \|Z\|^\ast{=} \sup_{c \gt 0} \frac{\mathbb{E}[Z\ln_q((Z/c)^{1/q} \vee 1) ]}{\ln_q \left(\frac{1}{1-\alpha} \mathbb{E} [(Z/c)^{1/q} \vee 1] \right)},\quad Z\in E', \end{equation}
\begin{equation} \|Z\|^\ast{=} \sup_{c \gt 0} \frac{\mathbb{E}[Z\ln_q((Z/c)^{1/q} \vee 1) ]}{\ln_q \left(\frac{1}{1-\alpha} \mathbb{E} [(Z/c)^{1/q} \vee 1] \right)},\quad Z\in E', \end{equation}
where ![]() $x\vee y = \max \{x, y\}$.
$x\vee y = \max \{x, y\}$.
Proof. The proof is similar to that of Theorem 4.4 in Ahmadi-Javid and Pichler [Reference Ahmadi-Javid and Pichler4]. For completeness, we give the details. Note that, for ![]() $Z\in E'$,
$Z\in E'$,
 \begin{align} \|Z\|^\ast & = \sup_{\mathrm{TsVaR}_{\alpha}(X) \le 1} \mathbb{E} [XZ] = \sup_{X\ne 0} \frac{\mathbb{E} [XZ]}{\mathrm{TsVaR}_{\alpha}(X)} \nonumber\\ & = \sup_{X \ne 0} \frac{\mathbb{E} [XZ]}{\inf_{\lambda \gt 0} \left\{ \lambda^{{-}1} \ln_q \left(\frac{1}{1-\alpha} \mathbb{E}[\exp_q(\lambda X)]\right) \right\}} \nonumber\\ & = \sup_{X \neq 0} \sup_{\lambda \gt 0}\frac{\mathbb{E} [\lambda XZ]}{\ln_q \left(\frac{1}{1-\alpha} \mathbb{E}[\exp_q(\lambda X)]\right) } \nonumber\\ & = \sup_{X \neq 0} \frac{\mathbb{E} [XZ]}{\ln_q \left(\frac{1}{1-\alpha} \mathbb{E}\left[\exp_q(X) \right]\right)}. \end{align}
\begin{align} \|Z\|^\ast & = \sup_{\mathrm{TsVaR}_{\alpha}(X) \le 1} \mathbb{E} [XZ] = \sup_{X\ne 0} \frac{\mathbb{E} [XZ]}{\mathrm{TsVaR}_{\alpha}(X)} \nonumber\\ & = \sup_{X \ne 0} \frac{\mathbb{E} [XZ]}{\inf_{\lambda \gt 0} \left\{ \lambda^{{-}1} \ln_q \left(\frac{1}{1-\alpha} \mathbb{E}[\exp_q(\lambda X)]\right) \right\}} \nonumber\\ & = \sup_{X \neq 0} \sup_{\lambda \gt 0}\frac{\mathbb{E} [\lambda XZ]}{\ln_q \left(\frac{1}{1-\alpha} \mathbb{E}[\exp_q(\lambda X)]\right) } \nonumber\\ & = \sup_{X \neq 0} \frac{\mathbb{E} [XZ]}{\ln_q \left(\frac{1}{1-\alpha} \mathbb{E}\left[\exp_q(X) \right]\right)}. \end{align}
For any ![]() $c \gt 0$, define
$c \gt 0$, define ![]() $X_c= \ln _q((Z/c)^{1/q} \vee 1)$. Then
$X_c= \ln _q((Z/c)^{1/q} \vee 1)$. Then ![]() $X_c\ge 0$ and
$X_c\ge 0$ and
 $$\|Z\|^* \ge \sup_{c \gt 0} \frac{\mathbb{E} [Z\ln_q((Z/c)^{1/q} \vee 1)]}{\ln_q \left(\frac{1}{1-\alpha} \mathbb{E} [(Z/c)^{1/q} \vee 1] \right)}.$$
$$\|Z\|^* \ge \sup_{c \gt 0} \frac{\mathbb{E} [Z\ln_q((Z/c)^{1/q} \vee 1)]}{\ln_q \left(\frac{1}{1-\alpha} \mathbb{E} [(Z/c)^{1/q} \vee 1] \right)}.$$
To obtain the converse inequality, from (4.9), it follows that ![]() $d\ge \|Z\|^\ast$ is equivalent to
$d\ge \|Z\|^\ast$ is equivalent to
We maximize the left-hand side of the above expression with respect to ![]() $X\ge 0$. The Lagrangian of this maximization problem is
$X\ge 0$. The Lagrangian of this maximization problem is
where ![]() $\mu$ is the Lagrange multiplier associated with the constraint
$\mu$ is the Lagrange multiplier associated with the constraint ![]() $X \ge 0$. The Lagrangian
$X \ge 0$. The Lagrangian ![]() $L$ is differentiable, and its directional derivative with respect to
$L$ is differentiable, and its directional derivative with respect to ![]() $X$ in direction
$X$ in direction ![]() $H \in E''$ is
$H \in E''$ is
The derivative vanishes in every direction ![]() $H$ so that
$H$ so that ![]() $Z - \mu = c [\exp _q(X)]^q$ with
$Z - \mu = c [\exp _q(X)]^q$ with ![]() $c = d (1-\alpha )^{q-1} [\mathbb {E}\exp _q(X)]^{-q} \gt 0$. By complimentary slackness for the optimal
$c = d (1-\alpha )^{q-1} [\mathbb {E}\exp _q(X)]^{-q} \gt 0$. By complimentary slackness for the optimal ![]() $X$ and
$X$ and ![]() $\mu$,
$\mu$,
which is equivalent to
This completes the proof of the theorem.
In the next proposition, we reconsider the domain of the objective function in (4.8).
Proposition 4.5. For ![]() $0 \lt q\le 1$ and
$0 \lt q\le 1$ and ![]() $0 \lt \alpha \lt 1$, the objective function
$0 \lt \alpha \lt 1$, the objective function
 $$h_{\alpha}(c) := \frac{\mathbb{E} [Z\ln_q((Z/c)^{1/q} \vee 1)]}{\ln_q \left(\frac{1}{1-\alpha} \mathbb{E}((Z/c)^{1/q} \vee 1) \right)}$$
$$h_{\alpha}(c) := \frac{\mathbb{E} [Z\ln_q((Z/c)^{1/q} \vee 1)]}{\ln_q \left(\frac{1}{1-\alpha} \mathbb{E}((Z/c)^{1/q} \vee 1) \right)}$$
in the expression of the dual norm (4.8) can be continuously extend to ![]() $[0, \infty )$, and
$[0, \infty )$, and
Furthermore, the supremum is attained at some ![]() $c \ge 0$. If
$c \ge 0$. If ![]() $Z\ne 0$ is bounded, then the optimal
$Z\ne 0$ is bounded, then the optimal ![]() $c$ satisfies
$c$ satisfies ![]() $0 \le c \lt \|Z\|_{\infty }$.
$0 \le c \lt \|Z\|_{\infty }$.
Proof. First, note that ![]() $h_{\alpha }(c)$ is continuous in
$h_{\alpha }(c)$ is continuous in ![]() $c\in (0,\infty )$ and
$c\in (0,\infty )$ and ![]() $h_{\alpha }(c) \ge 0$. Note that
$h_{\alpha }(c) \ge 0$. Note that
and ![]() $h_{\alpha }(c) \longrightarrow 0$ as
$h_{\alpha }(c) \longrightarrow 0$ as ![]() $c\to +\infty$. On the other hand, for
$c\to +\infty$. On the other hand, for ![]() $c\ge \|Z\|_{\infty }$, the numerator of
$c\ge \|Z\|_{\infty }$, the numerator of ![]() $h_\alpha$ is
$h_\alpha$ is ![]() $0$ and, hence,
$0$ and, hence, ![]() $h_\alpha (c) = 0$. Thus, the desired result follows from the continuity of
$h_\alpha (c) = 0$. Thus, the desired result follows from the continuity of ![]() $h_\alpha (\cdot )$ on
$h_\alpha (\cdot )$ on ![]() $[0, \|Z\|_\infty ]$.
$[0, \|Z\|_\infty ]$.
From Theorem 4.4, for given ![]() $Z\in E'$, we can identify a random variable
$Z\in E'$, we can identify a random variable ![]() $X^\ast \in E''$, which maximizes
$X^\ast \in E''$, which maximizes
Proposition 4.6. For ![]() $0 \lt q\le 1$ and
$0 \lt q\le 1$ and ![]() $0 \lt \alpha \lt 1$, let
$0 \lt \alpha \lt 1$, let ![]() $Z \in E'$, and suppose that
$Z \in E'$, and suppose that ![]() $c^\ast \gt 0$ be optimal in (4.8). Then,
$c^\ast \gt 0$ be optimal in (4.8). Then,
satisfies the equality
Proof. By (4.8) and (4.12), we have
 $$\|Z\|^* = \frac{\mathbb{E} [ZX]}{\ln_q \left(\frac{1}{1-\alpha} \mathbb{E} [\exp_q(X)] \right)}.$$
$$\|Z\|^* = \frac{\mathbb{E} [ZX]}{\ln_q \left(\frac{1}{1-\alpha} \mathbb{E} [\exp_q(X)] \right)}.$$
Thus,
where the inequalities follows from (4.11) and (3.1), respectively. This completes the proof.
For ![]() $0 \lt q\le 1$ and
$0 \lt q\le 1$ and ![]() $0 \lt \alpha \lt 1$, let
$0 \lt \alpha \lt 1$, let ![]() $X\in E''$ be fixed. How to identify a random variable
$X\in E''$ be fixed. How to identify a random variable ![]() $Z \in E'$, which maximizes
$Z \in E'$, which maximizes
Ahmadi-Javid and Pichler [Reference Ahmadi-Javid and Pichler4] gave a positive answer for ![]() $q=1$. It is still an open question for
$q=1$. It is still an open question for ![]() $0 \lt q \lt 1$.
$0 \lt q \lt 1$.
5. Conclusion
In this paper, we generalize the concept of EVaR, defined by Ahmadi-Javid [Reference Ahmadi-Javid2], to ![]() $\mathrm {TsVaR}$, using the generalized
$\mathrm {TsVaR}$, using the generalized ![]() $q$-logarithm and generalized
$q$-logarithm and generalized ![]() $q$-exponential functions.
$q$-exponential functions. ![]() $\mathrm {TsVaR}$ is not a coherent premium principle, even not a convex premium principle. This is caused by a lack of cash invariance in general. We show that in the class of
$\mathrm {TsVaR}$ is not a coherent premium principle, even not a convex premium principle. This is caused by a lack of cash invariance in general. We show that in the class of ![]() $\mathrm {TsVaR}$ with
$\mathrm {TsVaR}$ with ![]() $q \in (0, 1]$, only EVaR corresponding to
$q \in (0, 1]$, only EVaR corresponding to ![]() $q=1$ is a coherent premium principle. Dual representation for
$q=1$ is a coherent premium principle. Dual representation for ![]() $\mathrm {TsVaR}$ is established by using the variational representation for the generalized relative entropy, which is due to Ma and Tian [Reference Ma and Tian16]. We compare
$\mathrm {TsVaR}$ is established by using the variational representation for the generalized relative entropy, which is due to Ma and Tian [Reference Ma and Tian16]. We compare ![]() $\mathrm {TsVaR}$'s under different confidence levels
$\mathrm {TsVaR}$'s under different confidence levels ![]() $\alpha$ and obtain the strong monotonicity of
$\alpha$ and obtain the strong monotonicity of ![]() $\mathrm {TsVaR}$. Finally, we consider the norm and dual norm induced by
$\mathrm {TsVaR}$. Finally, we consider the norm and dual norm induced by ![]() $\mathrm {TsVaR}$ constrained on the related spaces
$\mathrm {TsVaR}$ constrained on the related spaces ![]() $E, E'$, and
$E, E'$, and ![]() $E''$, which are called the primal, dual, and bidual Tsallis spaces, respectively. It is proven that
$E''$, which are called the primal, dual, and bidual Tsallis spaces, respectively. It is proven that ![]() $(E, \|\cdot \|)$ and
$(E, \|\cdot \|)$ and ![]() $(E'', \|\cdot \|)$ are Banach spaces when the norm
$(E'', \|\cdot \|)$ are Banach spaces when the norm ![]() $\|\cdot \|$ is induced by
$\|\cdot \|$ is induced by ![]() $\mathrm {TsVaR}$. We also give the explicit formula of the dual
$\mathrm {TsVaR}$. We also give the explicit formula of the dual ![]() $\mathrm {TsVaR}$ norm.
$\mathrm {TsVaR}$ norm.
Acknowledgments
The authors are grateful to the Editor and one anonymous referee for their comprehensive reviews of an earlier version of this paper.
Funding Statement
T. Hu was supported by the National Natural Science Foundation of China (No. 71871208) and by Anhui Center for Applied Mathematics.
Conflict of interest
The authors declare no conflict of interest.
Appendix A
Proof of Proposition 2.1. We only prove part (4) since the others are trivial. Denote ![]() $\boldsymbol z =(z_1,\ldots, z_n) =(\exp _q(x_1), \ldots, \exp _q(x_n))$, and let
$\boldsymbol z =(z_1,\ldots, z_n) =(\exp _q(x_1), \ldots, \exp _q(x_n))$, and let ![]() $\boldsymbol {z}^\top$ represent the transpose of
$\boldsymbol {z}^\top$ represent the transpose of ![]() $\boldsymbol z$ and
$\boldsymbol z$ and ![]() $\boldsymbol 1 = (1, \dots, 1)$. Then, the Hessian matrix of
$\boldsymbol 1 = (1, \dots, 1)$. Then, the Hessian matrix of ![]() $f(\boldsymbol x)$ is
$f(\boldsymbol x)$ is
To prove that ![]() $f(\boldsymbol x)$ is convex, it suffices to show that for all
$f(\boldsymbol x)$ is convex, it suffices to show that for all ![]() $\boldsymbol v=(v_1, \ldots, v_n)$, we have
$\boldsymbol v=(v_1, \ldots, v_n)$, we have
 $$\boldsymbol v \nabla^2 f(\boldsymbol x) \boldsymbol v^\top = \frac{q}{(\boldsymbol 1 \boldsymbol z^\top )^{q+1}} \left [\left(\sum_{i=1}^n z_i \right) \left(\sum_{i=1}^n v_i^2 z_i^{2q-1} \right) - \left(\sum_{i=1}^n v_i z_i^q \right)^2\right ] \ge 0,$$
$$\boldsymbol v \nabla^2 f(\boldsymbol x) \boldsymbol v^\top = \frac{q}{(\boldsymbol 1 \boldsymbol z^\top )^{q+1}} \left [\left(\sum_{i=1}^n z_i \right) \left(\sum_{i=1}^n v_i^2 z_i^{2q-1} \right) - \left(\sum_{i=1}^n v_i z_i^q \right)^2\right ] \ge 0,$$
which follows from the Cauchy–Schwarz inequality.
Proof of Lemma 3.2. First note that the set ![]() $\{(X, \lambda ): \lambda \gt 0, \mathbb {E} [\exp _q(\lambda X)] \lt \infty \}$ is convex. Then, it suffices to show that for
$\{(X, \lambda ): \lambda \gt 0, \mathbb {E} [\exp _q(\lambda X)] \lt \infty \}$ is convex. Then, it suffices to show that for ![]() $\beta \in [0,1]$,
$\beta \in [0,1]$,
which can be rewrite as
 \begin{align*} & [\beta \lambda_1 + (1-\beta) \lambda_2] \ln_q \left[\frac{1}{\alpha} \mathbb{E}\left[\exp_q\left(\frac{\beta X + (1-\beta) Y}{\beta \lambda_1 + (1-\beta) \lambda_2}\right) \right]\right] \\ & \quad \le \beta \lambda_1 \ln_q \left[\frac{1}{\alpha} \mathbb{E}\left[\exp_q\left(\frac{X}{\lambda_1}\right) \right]\right] + (1-\beta) \lambda_2 \ln_q \left[\frac{1}{\alpha} \mathbb{E}\left[\exp_q\left(\frac{Y}{\lambda_2}\right) \right]\right]. \end{align*}
\begin{align*} & [\beta \lambda_1 + (1-\beta) \lambda_2] \ln_q \left[\frac{1}{\alpha} \mathbb{E}\left[\exp_q\left(\frac{\beta X + (1-\beta) Y}{\beta \lambda_1 + (1-\beta) \lambda_2}\right) \right]\right] \\ & \quad \le \beta \lambda_1 \ln_q \left[\frac{1}{\alpha} \mathbb{E}\left[\exp_q\left(\frac{X}{\lambda_1}\right) \right]\right] + (1-\beta) \lambda_2 \ln_q \left[\frac{1}{\alpha} \mathbb{E}\left[\exp_q\left(\frac{Y}{\lambda_2}\right) \right]\right]. \end{align*}
By Proposition 2.1(2), the above inequality reduces to
 \begin{align} & [\beta \lambda_1 + (1-\beta) \lambda_2] \ln_q \mathbb{E}\left[\exp_q\left(\frac{\beta X + (1-\beta) Y}{\beta \lambda_1 + (1-\beta) \lambda_2}\right) \right] \nonumber\\ & \quad \le \beta \lambda_1 \ln_q \mathbb{E}\left[\exp_q\left(\frac{X}{\lambda_1}\right) \right] + (1-\beta) \lambda_2 \ln_q \mathbb{E}\left[\exp_q\left(\frac{Y}{\lambda_2}\right) \right]. \end{align}
\begin{align} & [\beta \lambda_1 + (1-\beta) \lambda_2] \ln_q \mathbb{E}\left[\exp_q\left(\frac{\beta X + (1-\beta) Y}{\beta \lambda_1 + (1-\beta) \lambda_2}\right) \right] \nonumber\\ & \quad \le \beta \lambda_1 \ln_q \mathbb{E}\left[\exp_q\left(\frac{X}{\lambda_1}\right) \right] + (1-\beta) \lambda_2 \ln_q \mathbb{E}\left[\exp_q\left(\frac{Y}{\lambda_2}\right) \right]. \end{align}
Setting ![]() $\lambda = \beta \lambda _1+(1-\beta )\lambda _2$ and
$\lambda = \beta \lambda _1+(1-\beta )\lambda _2$ and ![]() $w=\beta \lambda _1/\lambda$, (A.1) is equivalent to
$w=\beta \lambda _1/\lambda$, (A.1) is equivalent to
which follows from Proposition 2.1(4). This completes the proof of the lemma.
Proof of Lemma 3.3. For any ![]() $\epsilon \gt 0$ and
$\epsilon \gt 0$ and ![]() $X, Y\in E''$, there exist
$X, Y\in E''$, there exist ![]() $\lambda _1, \lambda _2 \gt 0$ such that
$\lambda _1, \lambda _2 \gt 0$ such that ![]() $\mathbb {E} [\exp _q(\lambda _1 X)] \lt \infty$,
$\mathbb {E} [\exp _q(\lambda _1 X)] \lt \infty$, ![]() $\mathbb {E} [\exp _q(\lambda _2 Y)] \lt \infty$ and
$\mathbb {E} [\exp _q(\lambda _2 Y)] \lt \infty$ and
by using the continuity of ![]() $g_{\alpha }(X,\lambda )$ in
$g_{\alpha }(X,\lambda )$ in ![]() $\lambda \gt 0$. By Lemma 3.2,
$\lambda \gt 0$. By Lemma 3.2, ![]() $g_{\alpha }(X,\lambda )$ is convex in
$g_{\alpha }(X,\lambda )$ is convex in ![]() $(X,\lambda )$. So, for any
$(X,\lambda )$. So, for any ![]() $\beta \in [0,1]$,
$\beta \in [0,1]$,
 \begin{align*} \inf_{\lambda \gt 0} \{g_{\alpha}(\beta X + (1-\beta) Y,\lambda)\} & \le g_{\alpha}(\beta X + (1-\beta) Y,\beta \lambda_1 + (1-\beta) \lambda_2) \\ & \le \beta g_{\alpha}(X,\lambda_1) + (1-\beta) g_{\alpha}(Y,\lambda_2) \\ & \le \beta \inf_{\lambda \gt 0} \{g_{\alpha}(X,\lambda)\} + (1-\beta) \inf_{\lambda \gt 0} \{ g_{\alpha}(X,\lambda)\} + \epsilon. \end{align*}
\begin{align*} \inf_{\lambda \gt 0} \{g_{\alpha}(\beta X + (1-\beta) Y,\lambda)\} & \le g_{\alpha}(\beta X + (1-\beta) Y,\beta \lambda_1 + (1-\beta) \lambda_2) \\ & \le \beta g_{\alpha}(X,\lambda_1) + (1-\beta) g_{\alpha}(Y,\lambda_2) \\ & \le \beta \inf_{\lambda \gt 0} \{g_{\alpha}(X,\lambda)\} + (1-\beta) \inf_{\lambda \gt 0} \{ g_{\alpha}(X,\lambda)\} + \epsilon. \end{align*}
Therefore, the desired result follows by letting ![]() $\epsilon \downarrow 0$.
$\epsilon \downarrow 0$.
Proof of Lemma 3.7. We use the idea in the proof of Lemma 1.3 in Ahmadi-Javid [Reference Ahmadi-Javid1]. Define ![]() $f(x) = x^q \ln _q(x)$, and denote
$f(x) = x^q \ln _q(x)$, and denote ![]() $Y=\mathrm {d}\mathbb {Q}/\mathrm {d}\mathbb {P}$. Then (3.5) can be rewritten as
$Y=\mathrm {d}\mathbb {Q}/\mathrm {d}\mathbb {P}$. Then (3.5) can be rewritten as
where
 \begin{align*} L(\lambda) & = \inf_{Y \in S} \left\{-\mathbb{E} [XY^q]+\lambda\left(\mathbb{E} [f(Y)]-\alpha^{1-q}\ln_q \frac{1}{\alpha}\right)\right \} \\ & = \inf_{Y \in S} \{-\mathbb{E} [XY^q] + \lambda(\mathbb{E} [f(Y)] +\ln_q(\alpha))\} \end{align*}
\begin{align*} L(\lambda) & = \inf_{Y \in S} \left\{-\mathbb{E} [XY^q]+\lambda\left(\mathbb{E} [f(Y)]-\alpha^{1-q}\ln_q \frac{1}{\alpha}\right)\right \} \\ & = \inf_{Y \in S} \{-\mathbb{E} [XY^q] + \lambda(\mathbb{E} [f(Y)] +\ln_q(\alpha))\} \end{align*}
is the Lagrangian function associated with the optimization problem in the right-hand side, and ![]() $S = \{Y\in L_+^1: \mathbb {E}(Y) = 1\}$. Hence, it suffices to show that the optimal duality gap for optimization problem in the right-hand side is zero. This is possible by showing that the generalized Slater's constraint qualification in Jeyakumar and Wolkowicz [Reference Jeyakumar and Wolkowicz14] holds for this problem, that is, there exists
$S = \{Y\in L_+^1: \mathbb {E}(Y) = 1\}$. Hence, it suffices to show that the optimal duality gap for optimization problem in the right-hand side is zero. This is possible by showing that the generalized Slater's constraint qualification in Jeyakumar and Wolkowicz [Reference Jeyakumar and Wolkowicz14] holds for this problem, that is, there exists ![]() $\widehat {Y} \in L^1$ satisfying
$\widehat {Y} \in L^1$ satisfying ![]() $\mathbb {E} [\widehat {Y}] = 1$,
$\mathbb {E} [\widehat {Y}] = 1$, ![]() $\widehat {Y}\in L_+^1$, and
$\widehat {Y}\in L_+^1$, and ![]() $\mathbb {E} [f(\widehat {Y})] \lt \alpha ^{1-q} \ln _q (1/\alpha ) =-\ln _q(\alpha )$. Note that
$\mathbb {E} [f(\widehat {Y})] \lt \alpha ^{1-q} \ln _q (1/\alpha ) =-\ln _q(\alpha )$. Note that ![]() $\widehat {Y}= 1$ fulfills these conditions. Thus, we complete the proof of the lemma.
$\widehat {Y}= 1$ fulfills these conditions. Thus, we complete the proof of the lemma.