Contents
Research Article
ORDERING p-SPACINGS OF GENERALIZED ORDER STATISTICS REVISITED
-
- Published online by Cambridge University Press:
- 13 November 2008, pp. 1-16
-
- Article
- Export citation
STOCHASTIC ORDER OF SAMPLE RANGE FROM HETEROGENEOUS EXPONENTIAL RANDOM VARIABLES
-
- Published online by Cambridge University Press:
- 13 November 2008, pp. 17-29
-
- Article
- Export citation
SHARP TWO-SIDED BOUNDS FOR DISTRIBUTIONS UNDER A HAZARD RATE CONSTRAINT
-
- Published online by Cambridge University Press:
- 13 November 2008, pp. 31-36
-
- Article
- Export citation
PROPORTIONAL THREE-PERSON RED-AND-BLACK GAMES
-
- Published online by Cambridge University Press:
- 13 November 2008, pp. 37-50
-
- Article
- Export citation
OPTIMAL STOPPING IN A STOCHASTIC GAME
-
- Published online by Cambridge University Press:
- 13 November 2008, pp. 51-60
-
- Article
- Export citation
PERFORMANCE ESTIMATION OF M/DK/1 QUEUE UNDER FAIR SOJOURN PROTOCOL IN HEAVY TRAFFIC
-
- Published online by Cambridge University Press:
- 13 November 2008, pp. 61-74
-
- Article
- Export citation
q-SERIES IN MARKOV CHAINS WITH BINOMIAL TRANSITIONS: STUDYING A QUEUE WITH SYNCHRONIZATION
-
- Published online by Cambridge University Press:
- 13 November 2008, pp. 75-99
-
- Article
- Export citation
DYNAMIC ROUTING POLICIES FOR MULTISKILL CALL CENTERS
-
- Published online by Cambridge University Press:
- 13 November 2008, pp. 101-119
-
- Article
- Export citation
HITTING PROBABILITIES AND HITTING TIMES FOR STOCHASTIC FLUID FLOWS: THE BOUNDED MODEL
-
- Published online by Cambridge University Press:
- 13 November 2008, pp. 121-147
-
- Article
- Export citation
FUNCTIONALS OF BROWNIAN BRIDGES ARISING IN THE CURRENT MISMATCH IN D/A CONVERTERS
-
- Published online by Cambridge University Press:
- 13 November 2008, pp. 149-172
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PES volume 23 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
PES volume 23 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

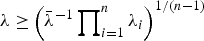 with
with 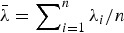 . Further, this usual stochastic order is strengthened to the hazard rate order for
. Further, this usual stochastic order is strengthened to the hazard rate order for 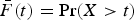 . An application to birth and death processes is discussed.
. An application to birth and death processes is discussed.