Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Giordano, Paolo
and
Kunzinger, Michael
2013.
New topologies on Colombeau generalized numbers and the Fermat–Reyes theorem.
Journal of Mathematical Analysis and Applications,
Vol. 399,
Issue. 1,
p.
229.
Hörmann, Günther
Konjik, Sanja
and
Kunzinger, Michael
2014.
Symplectic Modules Over Colombeau-Generalized Numbers.
Communications in Algebra,
Vol. 42,
Issue. 8,
p.
3558.
Hörmann, Günther
and
Sämann, Clemens
2014.
The globally hyperbolic metric splitting for non-smooth wave-type space-times.
Journal of Mathematical Analysis and Applications,
Vol. 420,
Issue. 1,
p.
348.
Khelif, A.
Scarpalezos, D.
and
Vernaeve, H.
2014.
Asymptotic Ideals (Ideals in the Ring of Colombeau Generalized Constants with Continuous Parametrization).
Communications in Algebra,
Vol. 42,
Issue. 6,
p.
2721.
Giordano, Paolo
and
Wu, Enxin
2015.
Categorical frameworks for generalized functions.
Arabian Journal of Mathematics,
Vol. 4,
Issue. 4,
p.
301.
Nigsch, Eduard A.
2017.
Nonlinear generalized sections and vector bundle homomorphisms in Colombeau spaces of generalized functions.
Mathematische Nachrichten,
Vol. 290,
Issue. 13,
p.
1991.
Sämann, Clemens
and
Steinbauer, Roland
2017.
Geodesics in nonexpanding impulsive gravitational waves with Λ. II.
Journal of Mathematical Physics,
Vol. 58,
Issue. 11,
Khelif, A.
and
Scarpalezos, D.
2021.
Maximal closed ideals of the Colombeau Algebra of Generalized functions.
Monatshefte für Mathematik,
Vol. 194,
Issue. 1,
p.
119.
Pilipović, Stevan
Scarpalézos, Dimitris
and
Vindas, Jasson
2023.
Besov regularity in non-linear generalized functions.
Monatshefte für Mathematik,
Vol. 201,
Issue. 2,
p.
483.
Fritz, Tobias
2024.
Differential geometry and general relativity with algebraifolds.
Journal of Geometry and Physics,
Vol. 206,
Issue. ,
p.
105327.
Sämann, Clemens
Schinnerl, Benedict
Steinbauer, Roland
and
Švarc, Robert
2024.
Cut-and-paste for impulsive gravitational waves with $$\Lambda $$: the mathematical analysis.
Letters in Mathematical Physics,
Vol. 114,
Issue. 2,

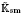 of generalized numbers in this unified setting. In particular, we investigate the ring and order structure of
of generalized numbers in this unified setting. In particular, we investigate the ring and order structure of 