An estimate for trigonometrical sums over square-free integers with a constant number of prime factors

Extract

1. In deriving an expression for the number of representations of a sufficiently large integer N in the form

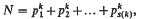
where k: is a positive integer, s(k) a suitably large function of k and p_i is a prime number, i = 1, 2, …, s(k), by Vinogradov's method it is necessary to obtain estimates for trigonometrical sums of the type

where ω = l/k and the real number a satisfies 0 ≦ α ≦ 1 and is “near” a rational number a/q, (a, q) = 1, with “large” denominator q. See Estermann (1), Chapter 3, for the case k = 1 or Hua (2), for the general case. The meaning of “near” and “arge” is made clear below—Lemma 4—as it is necessary for us to quote Hua's estimate. In this paper, in Theorem 1, an estimate is obtained for the trigonometrical sum

where α satisfies the same conditions as above and where π denotes a squarefree number with r prime factors. This estimate enables one to derive expressions for the number of representations of a sufficiently large integer N in the form

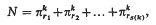
where s(k) has the same meaning as above and where π_ri, i = 1, 2, …, s(k), denotes a square-free integer with r_i prime factors.