Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T08:42:12.125Z Has data issue: false hasContentIssue false
  • English
  • Français

Dirichlet vs Neumann

Part of: Partial differential equations

Published online by Cambridge University Press:  22 November 2022

Eduard Marušić-Paloka
Eduard Marušić-Paloka*
Affiliation:
Department of mathematics, Faculty of Science and Mathematics, University of Zagreb, Bijenička 30, 10000 Zagreb, Croatia (emarusic@math.hr)
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the asymptotic behaviour of the periodically mixed Zaremba problem. We cover the part of the boundary by a chess board with a small period (square size) $\varepsilon$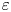 and impose the Dirichlet condition on black and the Neumann condition on white squares. As $\varepsilon \to 0$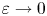, we get the effective boundary condition which is always of the Dirichlet type. The Dirichlet data on the boundary, however, depend on the ratio between the magnitudes of the two boundary values.

Keywords

periodic boundary conditionhomogenizationboundary layerLaplace equationthe Zaremba problem

MSC classification

Primary: 35B27: Homogenization; equations in media with periodic structure 35B25: Singular perturbations 35B40: Asymptotic behavior of solutions
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 4 , November 2022 , pp. 1063 - 1074
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bensoussan, A., Lions, J. L. and Papanicolau, G., Asymptotic analysis for periodic structures (North Holland, 1978).Google Scholar
Filo, J., A note on asymptotic expansion for periodic boundary condition, Arch Math. 34 (1998), 83–92.Google Scholar
Filo, J. and Luckhaus, S., Asymptotic expansion for a periodic boundary condition, J. Differ. Eq. 120 (1995), 133–173.CrossRefGoogle Scholar
Filo, J. and Luckhaus, S., Homogenization of a boundary condition for the heat equation, J. Eur. Math. Soc. 2 (2000), 217–258.CrossRefGoogle Scholar
Jäger, W. and Mikelić, A., On the roughness-induced effective boundary conditions for a viscous flow, J. Differ. Equ. 170 (2001), 96–122.CrossRefGoogle Scholar
Lions, J.l. and Magenes, E., Non-homogeneous boundary value problems and applications, Volume 1 (Springer, 1972).Google Scholar
Marušić-Paloka, E., Solvability of the Navier-Stokes system with $L^{2}$ boundary data, Appl. Math. Optim. 41 (2000), 365–375.CrossRefGoogle Scholar
Marušić-Paloka, E., Averaging the Navier's law on rapidly oscillating boundary, J. Math. Anal. Appl. 259 (2001), 685–701.CrossRefGoogle Scholar
Marušić-Paloka, E., Application of very weak formulation on homogenization of boundary value problems in porous media, Czech. Math. J. 71 (2021), 975–989.Google Scholar
Marušić-Paloka, E. and Pažanin, I., Rigorous justification of the effective boundary condition on a porous wall via homogenization, Z. Angew. Math. Phys. 72 (2021), 146.CrossRefGoogle Scholar
Marušić-Paloka, E. and Pažanin, I., Homogenization of a mixed boundary condition, Appl. Anal. 101 (2022), 4113–4125.CrossRefGoogle Scholar
Marušić-Paloka, E. and Pažanin, I., The effective boundary condition on a porous wall, Int. J. Eng. Sci. 173 (2022), 103638.CrossRefGoogle Scholar
Marušić-Paloka, E. and Starčević, M., High-order approximations for an incompressible viscous flow on a rough boundary, Appl. Anal.(0003–6811) 94 (2015), 1305–1333.CrossRefGoogle Scholar
Rjasanow, S. and Steinbach, O., The fast solution of boundary integral equations (Springer, 2007).Google Scholar
Sanchez-Palencia, E., Non-homogeneous media and vibration theory, Lecture Notes in Physics, Volume 127 (Springer, 1980).Google Scholar
Savaré, G., Regularity and perturbation results for mixed second order elliptic problems, Commun. Partial Differ. Eq. 22 (1997), 869–899.CrossRefGoogle Scholar
Tartar, L., An introduction to Sobolev spaces and interpolation spaces (Springer, 2007).Google Scholar