Published online by Cambridge University Press: 20 January 2009
This note is a sequel to the article by Mine (2) on the same problem.
I described in (1) a notation for indices of powers in non-associative algebra, defined the degree † and altitude of a power or index, and observed that powers can be represented by bifurcating root-trees. For example, the power xx.x is denoted x2 + 1, with index 2 + 1, and is represented by the tree 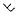 ; the degree (the number of factors, or free knots in the tree) is 3, and the altitude (the height of the tree) is 2. Multiplication being non-commutative or commutative, one maintains or ignores the distinction between left and right in the tree.
; the degree (the number of factors, or free knots in the tree) is 3, and the altitude (the height of the tree) is 2. Multiplication being non-commutative or commutative, one maintains or ignores the distinction between left and right in the tree.