Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T02:21:58.091Z Has data issue: false hasContentIssue false
  • English
  • Français

The Idempotent-separating Congruences on a Regular 0-bisimple Semigroup

Published online by Cambridge University Press:  20 January 2009

W. D. Munn
W. D. Munn
Affiliation:
University of Glasgow and University of Stirling
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A congruence ρ on a semigroup is said to be idempotent-separating if each ρ-class contains at most one idempotent. For any idempotent e of a semigroup S the set eSe is a subsemigroup of S with identity e and group of units He, the maximal subgroup of S containing e. The purpose of the present note is to show that if S is a regular O-bisimple semigroup and e is a non-zero idempotent of 5 then there is a one-to-one correspondence between the idempotentseparating congruences on 5 and the subgroups N of He with the property that aN ⊆ Na for all right units a of eSe and Nb ⊆ bN for all left units b of eSe. Some special cases of this result are discussed and, in the final section, an application is made to the principal factors of the full transformation semigroup 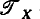on a set X.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 15 , Issue 3 , June 1967 , pp. 233 - 240
Copyright
Copyright © Edinburgh Mathematical Society 1967

References

REFERENCES

(1) Clifford, A. H. and Preston, G. B., The Algebraic Theory of Semigroups, vol. 1, Math. Surveys of the American Math. Soc. 7 (Providence, R.I., 1961).Google Scholar
(2) Lallement, G., Congruences et équivalences de Green sur un demi-groupe régulier, C.R. Acad. Sc. Paris, 262 (1966), 613–616.Google Scholar
(3) Mal'cev, A. I., Symmetric groupoids, Mat. Sbornik, 31 (73) (1952), 136–151.Google Scholar
(4) Preston, G. B., Congruences on completely 0-simple semigroups, Proc. London Math. Soc.. (3), 11 (1961), 557–576.CrossRefGoogle Scholar
(5) Rees, D., On the ideal structure of a semi-group satisfying a cancellation law, Quarterly J. Math. Oxford Ser. 19 (1948), 101–108.CrossRefGoogle Scholar
(6) Reilly, N. R. and Clifford, A. H., Bisimple inverse semigroups as semigroups of ordered triples (to appear).Google Scholar
(7) Warne, R. J., The idempotent-separating congruences of a bisimple inverse semigroup with identity (to appear).Google Scholar