Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T09:29:35.210Z Has data issue: false hasContentIssue false
  • English
  • Français

On a planar Schrödinger–Poisson system involving a non-symmetric potential

Part of: Elliptic equations and systems

Published online by Cambridge University Press:  05 December 2022

Riccardo Molle Open the ORCID record for Riccardo Molle [Opens in a new window]  and
Andrea Sardilli
Riccardo Molle
Affiliation:
Dipartimento di Matematica, Università di Roma “Tor Vergata”, Via della Ricerca Scientifica n. 1, 00133 Roma, Italy (molle@mat.uniroma2.it; andreasardilli6@gmail.com)
Andrea Sardilli
Affiliation:
Dipartimento di Matematica, Università di Roma “Tor Vergata”, Via della Ricerca Scientifica n. 1, 00133 Roma, Italy (molle@mat.uniroma2.it; andreasardilli6@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove the existence of a ground state positive solution of Schrödinger–Poisson systems in the plane of the form

\[ -\Delta u + V(x)u + \frac{\gamma}{2\pi} \left(\log|\cdot| \ast u^2 \right)u = b |u|^{p-2}u \quad\text{in}\ \mathbb{R}^2, \]
where $p\ge 4$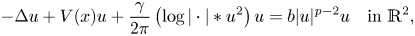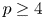, $\gamma,b>0$ 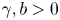and the potential $V$ 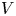is assumed to be positive and unbounded at infinity. On the potential we do not require any symmetry or periodicity assumption, and it is not supposed it has a limit at infinity. We approach the problem by variational methods, using a variant of the mountain pass theorem and the Cerami compactness condition.

Keywords

nonlinear Schrödinger–Poisson systemsplanar casepositive solutions

MSC classification

Primary: 35J50: Variational methods for elliptic systems 35J47: Second-order elliptic systems 35J10: Schrödinger operator 35J05: Laplacian operator, reduced wave equation (Helmholtz equation), Poisson equation
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 4 , November 2022 , pp. 1133 - 1146
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ambrosetti, A., Schrödinger-Poisson systems, Milan J. Math. 76 (2008), 257–274.CrossRefGoogle Scholar
Azzollini, A. and Pomponio, A., Ground state solutions for the nonlinear Schrödinger-Maxwell equations, J. Math. Anal. Appl. 345(1) (2008), 90–108.CrossRefGoogle Scholar
Bellazzini, J., Jeanjean, L. and Luo, T., Existence and instability of standing waves with prescribed norm for a class of Schrödinger–Poisson equations, Proc. Lond. Math. Soc. 107(3) (2013), 303–339.CrossRefGoogle Scholar
Bonheure, D., Cingolani, S. and Secchi, S., Concentration phenomena for the Schrödinger-Poisson system in ℝ2, Discrete Contin. Dyn. Syst. Ser. S 14(5) (2021), 1631–1648.Google Scholar
Brezis, H., Functional analysis, Sobolev spaces and partial differential equations (New York, Springer, 2011).CrossRefGoogle Scholar
Cao, D., Dai, W. and Zhang, Y., Existence and symmetry of solutions to 2-D Schrödinger-Newton equations, Dyn. Partial Differ. Equ. 18(2) (2021), 113–156.CrossRefGoogle Scholar
Cassani, D. and Tarsi, C., Schrödinger-Newton equations in dimension two via a Pohozaev-Trudinger log-weighted inequality, Calc. Var. Partial Differ. Equ. 60(5) (2021), 197.CrossRefGoogle Scholar
Cerami, G. and Molle, R., Positive bound state solutions for some Schrödinger-Poisson systems, Nonlinearity 29(10) (2016), 3103–3119.CrossRefGoogle Scholar
Cerami, G. and Molle, R., Multiple positive bound states for critical Schrödinger-Poisson systems, ESAIM Control Optim. Calc. Var. 25 (2019), 7–3.CrossRefGoogle Scholar
Cingolani, S. and Weth, T., On the planar Schrödinger-Poisson system, Ann. Inst. H. Poincaré C Anal. Non Linéaire 33(1) (2016), 169–197.CrossRefGoogle Scholar
Chen, W. and Pan, H., On the planar axially symmetric Schrödinger-Poisson systems with Choquard nonlinearity, J. Math. Anal. Appl. 504(1) (2021), 125378.CrossRefGoogle Scholar
Chen, S. and Tang, X., Axially symmetric solutions for the planar Schrödinger-Poisson system with critical exponential growth, J. Differ. Equ. 269(11) (2020), 9144–9174.CrossRefGoogle Scholar
Choquard, P., Stubbe, J. and Vuffray, M., Stationary solutions of the Schrödinger-Newton model – an ODE approach, Differ. Int. Equ. 21(7–8) (2008), 665–679.Google Scholar
Du, M., Weth, Tobias T., Ground states and high energy solutions of the planar Schrödinger-Poisson system, Nonlinearity 30(9) (2017), 3492–3515.CrossRefGoogle Scholar
Dutko, T., Mercuri, C. and Tyler, T. M., Groundstates and infinitely many high energy solutions to a class of nonlinear Schrödinger-Poisson systems, Calc. Var. Partial Differ. Equ. 60(5) (2021), 174.Google Scholar
Gilbarg, D. and Trudinger, N. S., Elliptic partial differential equations of second order (Berlin, Springer-Verlag, 2001).Google Scholar
Li, G. and Wang, C., The existence of a nontrivial solution to a nonlinear elliptic problem of linking type without the Ambrosetti-Rabinowitz condition, Ann. Acad. Sci. Fenn. Math. 36(2) (2011), 461–480.CrossRefGoogle Scholar
Lieb, E. H. and Loss, M., Analysis, 2nd edn. Graduate Studies in Mathematics, Volume 14 (American Mathematical Society, Providence, RI, 2001).Google Scholar
Lions, P.-L., The concentration-compactness principle in the calculus of variations. The locally compact case, part 2, Ann. Inst. H. Poincaré Anal. Non Linéaire 1(4) (1984), 223–283.CrossRefGoogle Scholar
Masaki, S., Local existence and WKB approximation of solutions to Schrödinger-Poisson system in the two-dimensional whole space, Comm. Partial Differ. Equ. 35(12) (2010), 2253–2278.CrossRefGoogle Scholar
Masaki, S., Energy solution to a Schrödinger–Poisson system in the two-dimensional whole space, SIAM J. Math. Anal. 43(6) (2011), 2719–2731.CrossRefGoogle Scholar
Pucci, P. and Serrin, J., The maximum principle, Progress in Nonlinear Differential Equations and their Applications, Volume 73 (Birkhäuser Verlag, Basel, 2007).CrossRefGoogle Scholar
Rabinowitz, P. H., On a class of nonlinear Schrödinger equations, Z. Angew. Math. Phys. 43(2) (1992), 270–291.CrossRefGoogle Scholar
Reed, M. and Simon, B., Methods of modern mathematical physics. IV. Analysis of operators (New York-London: Academic Press, 1978).Google Scholar
Ruiz, D., The Schrödinger-Poisson equation under the effect of a nonlinear local term, J. Funct. Anal. 237(2) (2006), 655–674.CrossRefGoogle Scholar
Sardilli, A., Master's degree thesis, Roma “Tor Vergata”, 2021.Google Scholar
Stubbe, J., Bound states of two-dimensional Schrödinger–Newton equations, e-print arXiv:0807.4059v1, 2008.Google Scholar