Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T09:04:14.119Z Has data issue: false hasContentIssue false
  • English
  • Français

On dense intermingling of exact overlaps and the open set condition

Part of: Classical measure theory

Published online by Cambridge University Press:  22 August 2022

Ian D. Morris
Ian D. Morris*
Affiliation:
School of Mathematical Sciences, Queen Mary, University of London, Mile End Road, London E1 4NS, UK (i.morris@qmul.ac.uk)
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that certain families of homogenous affine iterated function systems in $\mathbb {R}^{d}$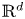 have the property that the open set condition and the existence of exact overlaps both occur densely in the space of translation parameters. These examples demonstrate that in the theorems of Falconer and Jordan–Pollicott–Simon on the almost sure dimensions of self-affine sets and measures, the set of exceptional translation parameters can be a dense set. The proof combines results from the literature on self-affine tilings of $\mathbb {R}^{d}$ 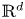with an adaptation of a classic argument of Erdős on the singularity of certain Bernoulli convolutions. This result encompasses a one-dimensional example due to Kenyon which arises as a special case.

Keywords

iterated function systemopen set conditionself-affine setself-affine tiling

MSC classification

Primary: 28A80: Fractals
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 3 , August 2022 , pp. 747 - 759
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bandt, C., Self-similar sets, V: integer matrices and fractal tilings of $\mathbb {R}^{n}$, Proc. Amer. Math. Soc. 112(2) (1991), 549–562.Google Scholar
Bandt, C. and Kravchenko, A., Differentiability of fractal curves, Nonlinearity 24(10) (2011), 2717–2728.CrossRefGoogle Scholar
Bárány, B., Hochman, M. and Rapaport, A., Hausdorff dimension of planar self-affine sets and measures, Invent. Math. 216(3) (2019), 601–659.CrossRefGoogle Scholar
Bedford, T., Crinkly curves, Markov partitions and box dimensions in self-similar sets. 1984. Thesis (Ph.D.), The University of WarwickGoogle Scholar
Das, T. and Simmons, D., The Hausdorff and dynamical dimensions of self-affine sponges: a dimension gap result, Invent. Math. 210(1) (2017), 85–134.CrossRefGoogle ScholarPubMed
Edgar, G. A., Fractal dimension of self-affine sets: some examples, Supplemento ai Rendiconti del Circolo matematico di Palermo 28 (1992), 341–358. Proceedings of the Conference Held at Oberwolfach, March 18–24, 1990.Google Scholar
Erdős, P., On a family of symmetric Bernoulli convolutions, Amer. J. Math. 61 (1939), 974–976.CrossRefGoogle Scholar
Falconer, K. J., The Hausdorff dimension of self-affine fractals, Math. Proc. Cambridge Philos. Soc. 103(2) (1988), 339–350.CrossRefGoogle Scholar
Feng, D.-J., Dimension of invariant measures for affine iterated function systems. Duke Math. J. To appear. Preprint arXiv:1901.0169Google Scholar
Feng, D.-J. and Käenmäki, A., Self-affine sets in analytic curves and algebraic surfaces, Ann. Acad. Sci. Fenn. Math. 43(1) (2018), 109–119.CrossRefGoogle Scholar
Feng, D.-J. and Wang, Y., A class of self-affine sets and self-affine measures, J. Fourier Anal. Appl. 11(1) (2005), 107–124.CrossRefGoogle Scholar
Fraser, J. M., On the packing dimension of box-like self-affine sets in the plane, Nonlinearity 25(7) (2012), 2075–2092.CrossRefGoogle Scholar
Hochman, M., On self-similar sets with overlaps and inverse theorems for entropy in $\mathbb {R}^{d}$, Mem. Amer. Math. Soc. 265 (2020), 1287.Google Scholar
Hochman, M. and Rapaport, A., Hausdorff dimension of planar self-affine sets and measures with overlaps, J. Eur. Math. Soc. 24 (2021), 2361–2441.CrossRefGoogle Scholar
Hutchinson, J. E., Fractals and self-similarity, Indiana Univ. Math. J. 30(5) (1981), 713–747.CrossRefGoogle Scholar
Jordan, T., Pollicott, M. and Simon, K., Hausdorff dimension for randomly perturbed self affine attractors, Comm. Math. Phys. 270(2) (2007), 519–544.CrossRefGoogle Scholar
Kenyon, R., Projecting the one-dimensional Sierpiński gasket, Israel J. Math. 97 (1997), 221–238.CrossRefGoogle Scholar
Knuth, D. E., The art of computer programming. Vol. 2.: seminumerical algorithms (Addison-Wesley, Reading, MA, 1998).Google Scholar
Lagarias, J. C. and Wang, Y., Integral self-affine tiles in $\mathbb {R}^{n}$, I: standard and nonstandard digit sets, J. London Math. Soc. (2) 54(1) (1996), 161–179.CrossRefGoogle Scholar
Lagarias, J. C. and Wang, Y., Self-affine tiles in $\mathbb { R}^{n}$, Adv. Math. 121(1) (1996), 21–49.CrossRefGoogle Scholar
Lau, K.-S. and Ngai, S.-M., Multifractal measures and a weak separation condition, Adv. Math. 141(1) (1999), 45–96.CrossRefGoogle Scholar
McMullen, C., The Hausdorff dimension of general Sierpiński carpets, Nagoya Math. J. 96 (1984), 1–9.CrossRefGoogle Scholar
Morris, I. D., On affine iterated function systems which robustly admit an invariant affine subspace. Proc. Amer. Math. Soc. To appear. Preprint arXiv:2111.02324Google Scholar
Ngai, S.-M. and Wang, Y., Hausdorff dimension of self-similar sets with overlaps, J. London Math. Soc. (2) 63(3) (2001), 655–672.CrossRefGoogle Scholar
Przytycki, F. and Urbański, M., On the Hausdorff dimension of some fractal sets, Studia Math. 93(2) (1989), 155–186.CrossRefGoogle Scholar
Simon, K. and Solomyak, B., On the dimension of self-similar sets, Fractals 10(1) (2002), 59–65.CrossRefGoogle Scholar
Solomyak, B., Measure and dimension for some fractal families, Math. Proc. Cambridge Philos. Soc. 124(3) (1998), 531–546.CrossRefGoogle Scholar
Zerner, M. P. W., Weak separation properties for self-similar sets, Proc. Amer. Math. Soc. 124(11) (1996), 3529–3539.CrossRefGoogle Scholar