Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cuevas, Claudio
Sepúlveda, Alex
and
Soto, Herme
2011.
Almost periodic and pseudo-almost periodic solutions to fractional differential and integro-differential equations.
Applied Mathematics and Computation,
Vol. 218,
Issue. 5,
p.
1735.
Maqbul, Md.
and
Bahuguna, D.
2012.
On the Stepanov-like Almost Automorphic Solutions of Abstract Differential Equations.
Differential Equations and Dynamical Systems,
Vol. 20,
Issue. 4,
p.
377.
Maqbul, Md.
and
Bahuguna, D.
2014.
Almost Periodic Solutions for Stepanov-Almost Periodic Differential Equations.
Differential Equations and Dynamical Systems,
Vol. 22,
Issue. 3,
p.
251.
Bedouhene, Fazia
Ibaouene, Youcef
Mellah, Omar
and
Raynaud de Fitte, Paul
2018.
Weyl almost periodic solutions to abstract linear and semilinear equations with Weyl almost periodic coefficients.
Mathematical Methods in the Applied Sciences,
Vol. 41,
Issue. 18,
p.
9546.
Shen, Shiping
and
Li, Yongkun
2020.
$$S^{p}$$-Almost Periodic Solutions of Clifford-Valued Fuzzy Cellular Neural Networks with Time-Varying Delays .
Neural Processing Letters,
Vol. 51,
Issue. 2,
p.
1749.
Huo, Nina
and
Li, Yongkun
2023.
Finite-timeSp-almost periodic synchronization of fractional-order octonion-valued Hopfield neural networks.
Chaos, Solitons & Fractals,
Vol. 173,
Issue. ,
p.
113721.

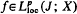 is said to be Stepanov-bounded or
is said to be Stepanov-bounded or