The Fibonacci groups are a special case of the following class of groups first studied by G. A. Miller (7). Given a natural number n, let θ be the automorphism of the free group F = 〈x1, …, xn |〉 of rank n which permutes the subscripts of the generators in accordance with the cycle (1, 2, …, n). Given a word w in F, let R be the smallest normal subgroup of F which contains w and is closed under θ. Then define Gn(w) = F/R and write An(w) for the derived factor group of Gn(w). Putting, for r ≦ 2, k ≦ 1,
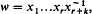
with subscripts reduced modulo n, we obtain the groups F(r, n, k) studied in (1) and (2), while the F(r, n, 1) are the ordinary Fibonacci groups F(r, n) of (3), (5) and (6). To conform with earlier notation, we write A(r, n, k) and A(r, n) for the derived factor groups of F(r, n, k), and F(r, n) respectively.