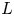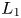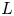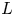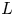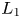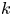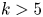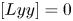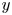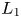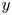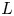1. Introduction
A thin Lie algebra is a graded Lie algebra $L=\bigoplus _{i=1}^{\infty }L_i$![]() with $\dim (L_1)=2$
with $\dim (L_1)=2$![]() and satisfying the following covering property: for each $i$
and satisfying the following covering property: for each $i$![]() , each non-zero $z\in L_i$
, each non-zero $z\in L_i$![]() satisfies $[zL_1]=L_{i+1}$
satisfies $[zL_1]=L_{i+1}$![]() . This implies at once that homogeneous components of a thin Lie algebra are at most two-dimensional. Those components of dimension two are called diamonds, hence $L_1$
. This implies at once that homogeneous components of a thin Lie algebra are at most two-dimensional. Those components of dimension two are called diamonds, hence $L_1$![]() is a diamond, and if there are no other diamonds then $L$
is a diamond, and if there are no other diamonds then $L$![]() is a graded Lie algebra of maximal class, see [Reference Caranti and Newman12, Reference Caranti, Mattarei and Newman14]. However, we adopt the convention of explicitly excluding graded Lie algebras of maximal class from the definition of thin Lie algebras. We also require thin Lie algebras to be infinite-dimensional in this paper.
is a graded Lie algebra of maximal class, see [Reference Caranti and Newman12, Reference Caranti, Mattarei and Newman14]. However, we adopt the convention of explicitly excluding graded Lie algebras of maximal class from the definition of thin Lie algebras. We also require thin Lie algebras to be infinite-dimensional in this paper.
Thus, a thin Lie algebra must have at least one further diamond past $L_1$![]() ; we let $L_k$
; we let $L_k$![]() be the earliest, and call it the second diamond. It turns out that $k$
be the earliest, and call it the second diamond. It turns out that $k$![]() can only be one of $3$
can only be one of $3$![]() , $5$
, $5$![]() , $q$
, $q$![]() , or $2q-1$
, or $2q-1$![]() , where $q$
, where $q$![]() is a power of the characteristic $p$
is a power of the characteristic $p$![]() when this is positive. This was proved in [Reference Avitabile and Jurman1], but a revised proof is given in [Reference Mattarei18]. The case of characteristic two, where only $3$
when this is positive. This was proved in [Reference Avitabile and Jurman1], but a revised proof is given in [Reference Mattarei18]. The case of characteristic two, where only $3$![]() and $2q-1$
and $2q-1$![]() can occur, is harder and was settled only in [Reference Avitabile, Jurman and Mattarei7]. In particular, only $3$
can occur, is harder and was settled only in [Reference Avitabile, Jurman and Mattarei7]. In particular, only $3$![]() and $5$
and $5$![]() can occur in characteristic zero. Among the various possibilities for $k$
can occur in characteristic zero. Among the various possibilities for $k$![]() , it is tempting to call the cases where $k$
, it is tempting to call the cases where $k$![]() is $3$
is $3$![]() or $5$
or $5$![]() the classical cases, as opposed to the values $q$
the classical cases, as opposed to the values $q$![]() and $2q-1$
and $2q-1$![]() , which are distinctly modular. The interpretation we provide in § 3 of our main result, Theorem 1, will lend further weight to this informal distinction. Note that in the theory of modular Lie algebras one calls classical those simple Lie algebras which are analogues of the simple Lie algebras of characteristic zero, including the exceptional ones.
, which are distinctly modular. The interpretation we provide in § 3 of our main result, Theorem 1, will lend further weight to this informal distinction. Note that in the theory of modular Lie algebras one calls classical those simple Lie algebras which are analogues of the simple Lie algebras of characteristic zero, including the exceptional ones.
Thin Lie algebras with $k$![]() equal to $3$
equal to $3$![]() or $5$
or $5$![]() , subject to a further restriction $\dim (L_4)=1$
, subject to a further restriction $\dim (L_4)=1$![]() in the former case, and excluding some small positive characteristics, were shown in [Reference Caranti, Mattarei, Newman and Scoppola13] to belong to (up to) three isomorphism types, associated with $p$
in the former case, and excluding some small positive characteristics, were shown in [Reference Caranti, Mattarei, Newman and Scoppola13] to belong to (up to) three isomorphism types, associated with $p$![]() -adic Lie groups of the classical types $A_1$
-adic Lie groups of the classical types $A_1$![]() and $A_2$
and $A_2$![]() (see [Reference Mattarei17] for matrix realizations of those groups). In contrast, the values $q$
(see [Reference Mattarei17] for matrix realizations of those groups). In contrast, the values $q$![]() and $2q-1$
and $2q-1$![]() for $k$
for $k$![]() occur for two broad classes of thin Lie algebras, of which various families were built from certain non-classical finite-dimensional simple modular Lie algebras, but also to other thin Lie algebras obtained from graded Lie algebras of maximal class through various constructions. General discussions of those two classes of thin Lie algebras may be found in [Reference Avitabile and Mattarei4] and [Reference Caranti and Mattarei11], respectively.
occur for two broad classes of thin Lie algebras, of which various families were built from certain non-classical finite-dimensional simple modular Lie algebras, but also to other thin Lie algebras obtained from graded Lie algebras of maximal class through various constructions. General discussions of those two classes of thin Lie algebras may be found in [Reference Avitabile and Mattarei4] and [Reference Caranti and Mattarei11], respectively.
The original motivation for the study of thin Lie algebras came from group theory. A pro-$p$![]() group $G$
group $G$![]() is called thin if $|G/\gamma _2(G)|=p^{2}$
is called thin if $|G/\gamma _2(G)|=p^{2}$![]() , and every open normal subgroup $H$
, and every open normal subgroup $H$![]() lies between two consecutive terms of the lower central series of $G$
lies between two consecutive terms of the lower central series of $G$![]() , in the sense that $\gamma _i(G)\ge H\ge \gamma _{i+1}(G)$
, in the sense that $\gamma _i(G)\ge H\ge \gamma _{i+1}(G)$![]() for some $i$
for some $i$![]() . It is not hard to see that a pro-$p$
. It is not hard to see that a pro-$p$![]() group $G$
group $G$![]() is thin if and only if the graded Lie ring $L$
is thin if and only if the graded Lie ring $L$![]() associated with its lower central series is a Lie algebra over the field $\mathbb {F}_p$
associated with its lower central series is a Lie algebra over the field $\mathbb {F}_p$![]() of $p$
of $p$![]() elements and satisfies the analogous condition on its graded ideals. In turn, the latter is easily seen to be equivalent to $L$
elements and satisfies the analogous condition on its graded ideals. In turn, the latter is easily seen to be equivalent to $L$![]() being a thin Lie algebra over $\mathbb {F}_p$
being a thin Lie algebra over $\mathbb {F}_p$![]() . According to [Reference Caranti, Mattarei, Newman and Scoppola13], the second diamond of the thin Lie algebra associated with a thin pro-$p$
. According to [Reference Caranti, Mattarei, Newman and Scoppola13], the second diamond of the thin Lie algebra associated with a thin pro-$p$![]() group may only occur in degree $3$
group may only occur in degree $3$![]() , $5$
, $5$![]() or $p$
or $p$![]() . A well-known example of thin pro-$p$
. A well-known example of thin pro-$p$![]() group is the Nottingham group over the field $\mathbb {F}_p$
group is the Nottingham group over the field $\mathbb {F}_p$![]() , with $p$
, with $p$![]() odd. Its associated thin Lie algebra has the second diamond in degree $p$
odd. Its associated thin Lie algebra has the second diamond in degree $p$![]() and, more generally, a diamond in each degree congruent to $1$
and, more generally, a diamond in each degree congruent to $1$![]() modulo $p-1$
modulo $p-1$![]() , see [Reference Caranti8]. Those results prompted investigations of thin Lie algebras as objects of independent study.
, see [Reference Caranti8]. Those results prompted investigations of thin Lie algebras as objects of independent study.
Our main result establishes a general fact for thin Lie algebras that was previously shown to hold for various special subclasses in ad hoc manners.
Theorem 1 Let $L$![]() be a thin Lie algebra with second diamond $L_k,$
be a thin Lie algebra with second diamond $L_k,$![]() where $k>5$
where $k>5$![]() . Then there is a non-zero element $y$
. Then there is a non-zero element $y$![]() of $L_1$
of $L_1$![]() such that $[Lyy]=0$
such that $[Lyy]=0$![]() .
.
Here we use the left-normed convention for iterated Lie products, hence $[abc]$![]() stands for $[[ab]c]$
stands for $[[ab]c]$![]() , and so $[Lyy]=0$
, and so $[Lyy]=0$![]() is another way of saying $(\operatorname {ad} y)^{2}=0$
is another way of saying $(\operatorname {ad} y)^{2}=0$![]() , where $\operatorname {ad}$
, where $\operatorname {ad}$![]() denotes the adjoint representation of $L$
denotes the adjoint representation of $L$![]() .
.
We will prove Theorem 1 in § 2, in an incremental way: we will gradually refine our hypotheses on $L$![]() to obtain partial results, working our way up to the assumption $k>5$
to obtain partial results, working our way up to the assumption $k>5$![]() of Theorem 1, and for each intermediate result there will be remarks showing by examples the necessity of the particular hypotheses assumed or motivating the next step.
of Theorem 1, and for each intermediate result there will be remarks showing by examples the necessity of the particular hypotheses assumed or motivating the next step.
According to a definition of Kostrikin, for $p\neq 2$![]() , the conclusion of Theorem 1 says that $y$
, the conclusion of Theorem 1 says that $y$![]() is a sandwich element (or simply a sandwich). Kostrikin introduced sandwich elements in the context of the Burnside problem, see [Reference Kostrikin16]. Four decades later, they played an important role in the classification theory of finite-dimensional simple modular Lie algebras in [Reference Premet and Strade20], especially for small characteristics (five and seven in this context). One remarkable property of sandwich elements, noted by Kostrikin and proved by Premet in [Reference Premet19], is that their presence in a finite-dimensional modular Lie algebra characterizes those simple Lie algebras which are not classical.
is a sandwich element (or simply a sandwich). Kostrikin introduced sandwich elements in the context of the Burnside problem, see [Reference Kostrikin16]. Four decades later, they played an important role in the classification theory of finite-dimensional simple modular Lie algebras in [Reference Premet and Strade20], especially for small characteristics (five and seven in this context). One remarkable property of sandwich elements, noted by Kostrikin and proved by Premet in [Reference Premet19], is that their presence in a finite-dimensional modular Lie algebra characterizes those simple Lie algebras which are not classical.
Although our thin Lie algebras are infinite-dimensional, a connection with finite-dimensional Lie algebras occurs via a loop algebra construction originating from [Reference Shalev22], which has then been used in several papers to build thin Lie algebras from finite-dimensional Lie algebras, simple or close to simple, with respect to certain cyclic gradings. In § 3, we discuss the relevance of the presence of a sandwich element in this context, and the connection with Premet's result.
For the sake of this Introduction, we outline the example of the thin Lie algebra $L$![]() associated with the Nottingham group, which has second diamond in degree $p$
associated with the Nottingham group, which has second diamond in degree $p$![]() . A realization of $L$
. A realization of $L$![]() was given in [Reference Caranti8] as a loop algebra of the $p$
was given in [Reference Caranti8] as a loop algebra of the $p$![]() -dimensional Witt simple algebra $W=W(1;1)$
-dimensional Witt simple algebra $W=W(1;1)$![]() over $\mathbb {F}_p$
over $\mathbb {F}_p$![]() , which is simply $\operatorname {Der}\bigl (\mathbb {F}_p[X]/(X^{p})\bigr )$
, which is simply $\operatorname {Der}\bigl (\mathbb {F}_p[X]/(X^{p})\bigr )$![]() . Because $W$
. Because $W$![]() has a grading over the integers, and a $\mathbb {Z}$
has a grading over the integers, and a $\mathbb {Z}$![]() -graded basis $E_i$
-graded basis $E_i$![]() for $-1\le i\le p-2$
for $-1\le i\le p-2$![]() (with $E_i=X^{i+1}\,d/dX$
(with $E_i=X^{i+1}\,d/dX$![]() , say), degree reasons show $E_{p-2}$
, say), degree reasons show $E_{p-2}$![]() is a sandwich element of $W$
is a sandwich element of $W$![]() if $p>3$
if $p>3$![]() (whence $W$
(whence $W$![]() is not classical if $p>3$
is not classical if $p>3$![]() ). In fact, in this case, the sandwich element $y$
). In fact, in this case, the sandwich element $y$![]() of $L$
of $L$![]() referred to in Theorem 1 is closely related to the element $E_{p-2}$
referred to in Theorem 1 is closely related to the element $E_{p-2}$![]() of $W$
of $W$![]() .
.
2. A sandwich element in thin Lie algebras
A sandwich element of a Lie algebra $L$![]() is a non-zero element $c\in L$
is a non-zero element $c\in L$![]() such that $(\operatorname {ad} c)^{2}=0$
such that $(\operatorname {ad} c)^{2}=0$![]() and $(\operatorname {ad} c)(\operatorname {ad} z)(\operatorname {ad} c)=0$
and $(\operatorname {ad} c)(\operatorname {ad} z)(\operatorname {ad} c)=0$![]() for all $z\in L$
for all $z\in L$![]() . The latter requirement (from which the name originates) is superfluous in characteristic different from two, as it follows from the former due to $[u[zcc]]=[uzcc]-2[uczc]+[uccz]$
. The latter requirement (from which the name originates) is superfluous in characteristic different from two, as it follows from the former due to $[u[zcc]]=[uzcc]-2[uczc]+[uccz]$![]() for $u,\,z\in L$
for $u,\,z\in L$![]() .
.
In the context of thin Lie algebras, it turns out that a non-zero element $y$![]() of $C_{L_1}(L_2)$
of $C_{L_1}(L_2)$![]() satisfies $[Lyy]=0$
satisfies $[Lyy]=0$![]() in most cases, as our Theorem 1 states, and so $y$
in most cases, as our Theorem 1 states, and so $y$![]() is a sandwich element if the characteristic is not two. This fact was crucial in the theory of graded Lie algebras of maximal class of [Reference Caranti, Mattarei and Newman14] and [Reference Caranti and Newman12], making a theory of constituents possible, although the sandwich point of view was not explicitly mentioned there. In particular, [Reference Caranti, Mattarei and Newman14, Lemma 3.3] can be restated as follows: if $L$
is a sandwich element if the characteristic is not two. This fact was crucial in the theory of graded Lie algebras of maximal class of [Reference Caranti, Mattarei and Newman14] and [Reference Caranti and Newman12], making a theory of constituents possible, although the sandwich point of view was not explicitly mentioned there. In particular, [Reference Caranti, Mattarei and Newman14, Lemma 3.3] can be restated as follows: if $L$![]() is a graded Lie algebra of maximal class, with the centralizer $C_{L_1}(L_2)$
is a graded Lie algebra of maximal class, with the centralizer $C_{L_1}(L_2)$![]() spanned by an element $y$
spanned by an element $y$![]() , with $[L_{i-1}y]=0$
, with $[L_{i-1}y]=0$![]() and $[L_iy]\neq 0$
and $[L_iy]\neq 0$![]() for some $i$
for some $i$![]() , then $[L_{i+1}y]=0$
, then $[L_{i+1}y]=0$![]() , whence $[L_iyy]=0$
, whence $[L_iyy]=0$![]() . A remarkable consequence of this fact is $[Lyy]=0$
. A remarkable consequence of this fact is $[Lyy]=0$![]() , which means $(\operatorname {ad} y)^{2}=0$
, which means $(\operatorname {ad} y)^{2}=0$![]() , and so $y$
, and so $y$![]() is a sandwich element if the characteristic is not two.
is a sandwich element if the characteristic is not two.
Our main goal in this section is showing that such a non-zero element $y$![]() of $C_{L_1}(L_2)$
of $C_{L_1}(L_2)$![]() is frequently a sandwich element also in a thin Lie algebra $L$
is frequently a sandwich element also in a thin Lie algebra $L$![]() , under certain assumptions which we introduce and justify along the way. If $L$
, under certain assumptions which we introduce and justify along the way. If $L$![]() has second diamond $L_3$
has second diamond $L_3$![]() , then $C_{L_1}(L_2)=0$
, then $C_{L_1}(L_2)=0$![]() , hence we must take $\dim (L_3)=1$
, hence we must take $\dim (L_3)=1$![]() as minimal assumption for our discussion, and then $\dim \bigl (C_{L_1}(L_2)\bigr )=1$
as minimal assumption for our discussion, and then $\dim \bigl (C_{L_1}(L_2)\bigr )=1$![]() . Taking then for $y$
. Taking then for $y$![]() a non-zero element of $C_{L_1}(L_2)$
a non-zero element of $C_{L_1}(L_2)$![]() and extending to a basis $x,\,y$
and extending to a basis $x,\,y$![]() of $L_1$
of $L_1$![]() , as we do without further mention in this section, we have $[xyy]=0$
, as we do without further mention in this section, we have $[xyy]=0$![]() .
.
When $L$![]() has characteristic two, we limit ourselves to the following simple observation, which (abundantly) covers the case of characteristic two in Theorem 1.
has characteristic two, we limit ourselves to the following simple observation, which (abundantly) covers the case of characteristic two in Theorem 1.
Proposition 2 Let $L$![]() be a thin Lie algebra of characteristic two, with $\dim (L_3)=1$
be a thin Lie algebra of characteristic two, with $\dim (L_3)=1$![]() , and let $y$
, and let $y$![]() span $C_{L_1}(L_2)$
span $C_{L_1}(L_2)$![]() . Then $[Lyy]=0$
. Then $[Lyy]=0$![]() .
.
Proof. Because $(\operatorname {ad} y)^{2}$![]() is a derivation of $L$
is a derivation of $L$![]() , its kernel is a subalgebra. However, because $[xyy]=0$
, its kernel is a subalgebra. However, because $[xyy]=0$![]() , both generators $x$
, both generators $x$![]() and $y$
and $y$![]() of $L$
of $L$![]() belong to the kernel, and hence that is the whole of $L$
belong to the kernel, and hence that is the whole of $L$![]() .
.
We will show that Proposition 2 extends to arbitrary characteristic if we include a further hypothesis $\dim (L_5)=1$![]() . Together with $\dim (L_3)=1$
. Together with $\dim (L_3)=1$![]() , this amounts to requiring that the second diamond of $L$
, this amounts to requiring that the second diamond of $L$![]() occurs later than $L_5$
occurs later than $L_5$![]() , as we assumed in Theorem 1. A justification for that hypothesis will emerge as we gradually work towards a proof. We start with suitably extending the conclusion $[L_iyy]=0$
, as we assumed in Theorem 1. A justification for that hypothesis will emerge as we gradually work towards a proof. We start with suitably extending the conclusion $[L_iyy]=0$![]() of [Reference Caranti, Mattarei and Newman14, Lemma 3.3], which was about graded Lie algebras of maximal class, to certain homogeneous components of any thin Lie algebra $L$
of [Reference Caranti, Mattarei and Newman14, Lemma 3.3], which was about graded Lie algebras of maximal class, to certain homogeneous components of any thin Lie algebra $L$![]() with $\dim (L_3)=1$
with $\dim (L_3)=1$![]() .
.
Lemma 3 Let $L$![]() be a thin Lie algebra with $\dim (L_3)=1$
be a thin Lie algebra with $\dim (L_3)=1$![]() , and let $y$
, and let $y$![]() span $C_{L_1}(L_2)$
span $C_{L_1}(L_2)$![]() . Let $L_i$
. Let $L_i$![]() be a homogeneous component with $[L_iy]\neq 0$
be a homogeneous component with $[L_iy]\neq 0$![]() , and suppose $L_{i-1}$
, and suppose $L_{i-1}$![]() has a non-zero element $u$
has a non-zero element $u$![]() with $[uy]=0$
with $[uy]=0$![]() . Then $[L_iyy]=0$
. Then $[L_iyy]=0$![]() . Moreover, $L_i$
. Moreover, $L_i$![]() and $L_{i+2}$
and $L_{i+2}$![]() have dimension one.
have dimension one.
Proof. Because of the covering property, $L_i$![]() is spanned by $[ux]$
is spanned by $[ux]$![]() , and hence has dimension one. From
, and hence has dimension one. From
it follows that $[L_iyy]=0$![]() . Because $[uxy]\neq 0$
. Because $[uxy]\neq 0$![]() by hypothesis, the covering property implies that $L_{i+2}$
by hypothesis, the covering property implies that $L_{i+2}$![]() is spanned by $[uxyx]$
is spanned by $[uxyx]$![]() , and hence has dimension one.
, and hence has dimension one.
The following immediate consequence of Lemma 3 resembles the formulation of [Reference Caranti, Mattarei and Newman14, Lemma 3.3] more closely.
Corollary 4 Let $L$![]() be a thin Lie algebra with $\dim (L_3)=1,$
be a thin Lie algebra with $\dim (L_3)=1,$![]() and let $y$
and let $y$![]() span $C_{L_1}(L_2)$
span $C_{L_1}(L_2)$![]() . If $L_{i-1}$
. If $L_{i-1}$![]() has a non-zero element centralized by $y,$
has a non-zero element centralized by $y,$![]() and $L_i$
and $L_i$![]() has none, then $L_{i+1}$
has none, then $L_{i+1}$![]() has such an element as well.
has such an element as well.
Equivalently, in a thin Lie algebra with $\dim (L_3)=1$![]() , at least one of any two consecutive homogeneous components has a non-zero element centralized by $y$
, at least one of any two consecutive homogeneous components has a non-zero element centralized by $y$![]() . Corollary 4 is often useful as a simple but weaker replacement for Lemma 3. However, we need the full strength of Lemma 3 in order to deduce the following consequence.
. Corollary 4 is often useful as a simple but weaker replacement for Lemma 3. However, we need the full strength of Lemma 3 in order to deduce the following consequence.
Corollary 5 Let $L$![]() be a thin Lie algebra with $\dim (L_3)=1,$
be a thin Lie algebra with $\dim (L_3)=1,$![]() and let $y$
and let $y$![]() span $C_{L_1}(L_2)$
span $C_{L_1}(L_2)$![]() . Suppose $\dim (L_j)=2$
. Suppose $\dim (L_j)=2$![]() for some $j>1$
for some $j>1$![]() . Then $\dim (L_{j-1})=1$
. Then $\dim (L_{j-1})=1$![]() and $[L_{j-1}yy]=0$
and $[L_{j-1}yy]=0$![]() . In particular, $L_j$
. In particular, $L_j$![]() contains a non-zero element centralized by $y$
contains a non-zero element centralized by $y$![]() .
.
Proof. Because of the covering property $L_{j-1}$![]() cannot contain any non-zero element centralized by $y$
cannot contain any non-zero element centralized by $y$![]() . Hence $L_{j-2}$
. Hence $L_{j-2}$![]() does contain a non-zero element $u$
does contain a non-zero element $u$![]() with $[uy]=0$
with $[uy]=0$![]() . Consequently, $v=[ux]$
. Consequently, $v=[ux]$![]() spans $L_{j-1}$
spans $L_{j-1}$![]() , and $[vyy]=0$
, and $[vyy]=0$![]() according to Lemma 3. Because $\dim (L_j)=2$
according to Lemma 3. Because $\dim (L_j)=2$![]() , the element $[vy]$
, the element $[vy]$![]() of $L_j$
of $L_j$![]() is non-zero and is centralized by $y$
is non-zero and is centralized by $y$![]() as desired.
as desired.
In particular, Corollary 5 implies that two consecutive components in a thin Lie algebra $L$![]() with $\dim (L_3)=1$
with $\dim (L_3)=1$![]() cannot both be diamonds. Thus, the distance between any two consecutive diamonds, by which we mean the difference of their degrees, is at least two.
cannot both be diamonds. Thus, the distance between any two consecutive diamonds, by which we mean the difference of their degrees, is at least two.
An easily proved consequence of this fact is that any thin Lie algebra $L$![]() with $\dim (L_3)=1$
with $\dim (L_3)=1$![]() remains thin under base field extensions. By contrast, this property fails for a thin Lie algebra $L$
remains thin under base field extensions. By contrast, this property fails for a thin Lie algebra $L$![]() with two diamonds occurring as consecutive homogeneous components. This latter fact was never explicitly recorded but was in essence understood since [Reference Caranti, Mattarei, Newman and Scoppola13], through an explicit calculation showing that the covering property is a quadratic condition in this case, rather than linear. We briefly digress from our main goal to state that result formally, and express its proof in a coordinate-free way.
with two diamonds occurring as consecutive homogeneous components. This latter fact was never explicitly recorded but was in essence understood since [Reference Caranti, Mattarei, Newman and Scoppola13], through an explicit calculation showing that the covering property is a quadratic condition in this case, rather than linear. We briefly digress from our main goal to state that result formally, and express its proof in a coordinate-free way.
Proposition 6 Let $L$![]() be a thin Lie algebra having two consecutive homogeneous components which are both diamonds. Then $L$
be a thin Lie algebra having two consecutive homogeneous components which are both diamonds. Then $L$![]() ceases to be thin after a suitable quadratic field extension.
ceases to be thin after a suitable quadratic field extension.
Proof. For any graded Lie algebra $L=\bigoplus _{i=1}^{\infty }L_i$![]() we may consider the linear maps $\psi _j:L_j\to \operatorname {Hom}_F(L_1,\,L_{j+1})$
we may consider the linear maps $\psi _j:L_j\to \operatorname {Hom}_F(L_1,\,L_{j+1})$![]() obtained by restriction from the adjoint representation. When $L$
obtained by restriction from the adjoint representation. When $L$![]() is thin with $L_j$
is thin with $L_j$![]() and $L_{j+1}$
and $L_{j+1}$![]() both diamonds, the covering property for the homogeneous component $L_j$
both diamonds, the covering property for the homogeneous component $L_j$![]() means that $\psi _j(L_j)$
means that $\psi _j(L_j)$![]() is a two-dimensional subspace of $\operatorname {Hom}_F(L_1,\,L_{j+1})$
is a two-dimensional subspace of $\operatorname {Hom}_F(L_1,\,L_{j+1})$![]() such that every non-zero element is a surjective linear map. Upon composing with a linear bijection $L_{j+1}\to L_1$
such that every non-zero element is a surjective linear map. Upon composing with a linear bijection $L_{j+1}\to L_1$![]() , whose choice is immaterial, we may view that as a two-dimensional subspace of $\operatorname {Hom}_F(L_1,\,L_1)$
, whose choice is immaterial, we may view that as a two-dimensional subspace of $\operatorname {Hom}_F(L_1,\,L_1)$![]() where every non-zero element has non-zero determinant. In terms of the associated projective spaces, $P\bigl (\psi _j(L_j)\bigr )$
where every non-zero element has non-zero determinant. In terms of the associated projective spaces, $P\bigl (\psi _j(L_j)\bigr )$![]() is then a one-dimensional projective subspace of the three-dimensional projective space $P\bigl (\operatorname {Hom}_F(L_1,\,L_1)\bigr )$
is then a one-dimensional projective subspace of the three-dimensional projective space $P\bigl (\operatorname {Hom}_F(L_1,\,L_1)\bigr )$![]() , disjoint from the non-degenerate quadric given by the zeroes of the determinant map. This condition will be violated under a suitable quadratic extension of the base field of $L$
, disjoint from the non-degenerate quadric given by the zeroes of the determinant map. This condition will be violated under a suitable quadratic extension of the base field of $L$![]() .
.
The same argument in the proof of Proposition 6 also shows that a thin Lie algebra over a quadratically closed field (a field without extensions of degree two) cannot have two diamonds occurring as consecutive homogeneous components. In fact, the thin Lie algebras studied in [Reference Avitabile, Caranti, Gavioli, Monti, Newman and O'Brien6, Reference Gavioli, Monti and Young15], where all homogeneous components except $L_2$![]() are diamonds, require their base field to have a quadratic field extension.
are diamonds, require their base field to have a quadratic field extension.
Returning to our main line of investigation, Corollary 5 is relevant in assigning types to diamonds of a thin Lie algebra. The type of a diamond $L_j$![]() is a scalar in the underlying field, or possibly the symbol $\infty$
is a scalar in the underlying field, or possibly the symbol $\infty$![]() , which describes certain relations holding in degree $j+1$
, which describes certain relations holding in degree $j+1$![]() . When this is done properly (that is, including fake diamonds, see Remark 13 below), the Lie product of a thin Lie algebra (and hence its isomorphism type) is completely determined by specifying all degrees where diamonds occur, and their types. In various notable instances of thin Lie algebras, diamonds occur at regular distances, and their types follow a periodic pattern, such as an arithmetic progression. Attaching types to diamonds needs to be done in different ways according to whether the second diamond occurs in degree $q$
. When this is done properly (that is, including fake diamonds, see Remark 13 below), the Lie product of a thin Lie algebra (and hence its isomorphism type) is completely determined by specifying all degrees where diamonds occur, and their types. In various notable instances of thin Lie algebras, diamonds occur at regular distances, and their types follow a periodic pattern, such as an arithmetic progression. Attaching types to diamonds needs to be done in different ways according to whether the second diamond occurs in degree $q$![]() or $2q-1$
or $2q-1$![]() , and was originally introduced in [Reference Caranti and Mattarei10] and [Reference Caranti and Mattarei9], respectively. However, in both cases, necessary conditions for a diamond $L_j$
, and was originally introduced in [Reference Caranti and Mattarei10] and [Reference Caranti and Mattarei9], respectively. However, in both cases, necessary conditions for a diamond $L_j$![]() to be assigned a type were $\dim (L_{j-1})=1$
to be assigned a type were $\dim (L_{j-1})=1$![]() and $[L_{j-1}yy]=0$
and $[L_{j-1}yy]=0$![]() (the latter being one of the relations assumed in degree $j+1$
(the latter being one of the relations assumed in degree $j+1$![]() ). Corollary 5 now ensures that those conditions hold in any thin Lie algebra with $\dim (L_3)=1$
). Corollary 5 now ensures that those conditions hold in any thin Lie algebra with $\dim (L_3)=1$![]() .
.
Now we use Lemma 3 to prove that if $L$![]() is thin with $\dim (L_3)=1$
is thin with $\dim (L_3)=1$![]() , then $[L_iyy]=0$
, then $[L_iyy]=0$![]() for all one-dimensional components $L_i$
for all one-dimensional components $L_i$![]() .
.
Lemma 7 Let $L$![]() be a thin Lie algebra with $\dim (L_3)=1,$
be a thin Lie algebra with $\dim (L_3)=1,$![]() and let $y$
and let $y$![]() span $C_{L_1}(L_2)$
span $C_{L_1}(L_2)$![]() . Suppose $[L_jyy]\neq 0$
. Suppose $[L_jyy]\neq 0$![]() for some $j$
for some $j$![]() . Then $\dim (L_j)=2$
. Then $\dim (L_j)=2$![]() .
.
Proof. Note that $j>2$![]() . If $L_{j-1}$
. If $L_{j-1}$![]() had a non-zero element centralized by $y$
had a non-zero element centralized by $y$![]() , then because $[L_jy]\neq 0$
, then because $[L_jy]\neq 0$![]() by hypothesis, Lemma 3 would apply with $i=j$
by hypothesis, Lemma 3 would apply with $i=j$![]() and yield $[L_jyy]=0$
and yield $[L_jyy]=0$![]() , a contradiction. Therefore, $L_{j-1}$
, a contradiction. Therefore, $L_{j-1}$![]() does not have any non-zero element centralized by $y$
does not have any non-zero element centralized by $y$![]() . Then because of Corollary 4 each of $L_{j-2}$
. Then because of Corollary 4 each of $L_{j-2}$![]() and $L_{j}$
and $L_{j}$![]() has such an element. In particular, because $[L_jy]\neq 0$
has such an element. In particular, because $[L_jy]\neq 0$![]() , we must have $\dim (L_j)=2$
, we must have $\dim (L_j)=2$![]() .
.
Thus, the task of proving $[Lyy]=0$![]() in a thin Lie algebra $L$
in a thin Lie algebra $L$![]() has now been reduced to showing $[L_jyy]=0$
has now been reduced to showing $[L_jyy]=0$![]() for the diamonds $L_j$
for the diamonds $L_j$![]() . We pause to note that $L$
. We pause to note that $L$![]() having any two diamonds at distance two implies $[Lyy]\neq 0$
having any two diamonds at distance two implies $[Lyy]\neq 0$![]() . In fact, if $L_j$
. In fact, if $L_j$![]() and $L_{j+2}$
and $L_{j+2}$![]() are diamonds, in a thin Lie algebra $L$
are diamonds, in a thin Lie algebra $L$![]() with $\dim (L_3)=1$
with $\dim (L_3)=1$![]() , then the covering property implies $[L_jy]\neq 0$
, then the covering property implies $[L_jy]\neq 0$![]() : the map $\psi _j$
: the map $\psi _j$![]() of the proof of Proposition 6 is always injective because of the covering property, but it would not be surjective if we had $[L_jy]=0$
of the proof of Proposition 6 is always injective because of the covering property, but it would not be surjective if we had $[L_jy]=0$![]() , and this is impossible here by dimension reasons as $\dim (L_{j+1})=1$
, and this is impossible here by dimension reasons as $\dim (L_{j+1})=1$![]() . Consequently, we have $[L_jy]=L_{j+1}$
. Consequently, we have $[L_jy]=L_{j+1}$![]() , and then $[L_jyy]=[L_{j+1}y]\neq 0$
, and then $[L_jyy]=[L_{j+1}y]\neq 0$![]() because $[L_{j+1}y]$
because $[L_{j+1}y]$![]() and $[L_{j+1}y]$
and $[L_{j+1}y]$![]() span the diamond $L_{j+2}$
span the diamond $L_{j+2}$![]() .
.
The following remark describes one special thin Lie algebra with $\dim (L_3)=1$![]() having certain diamonds at distance two.
having certain diamonds at distance two.
Remark 8 The proof of [Reference Caranti, Mattarei, Newman and Scoppola13, Theorem 2(a)] implies that in characteristic either zero or larger than five there is a unique (infinite-dimensional) thin Lie algebra $L$![]() having second diamond $L_5$
having second diamond $L_5$![]() . That result, which predates the study of thin Lie algebras per se, only claims uniqueness for the graded Lie algebra $L$
. That result, which predates the study of thin Lie algebras per se, only claims uniqueness for the graded Lie algebra $L$![]() associated with the lower central series of a infinite thin pro-$p$
associated with the lower central series of a infinite thin pro-$p$![]() group with second diamond in weight $5$
group with second diamond in weight $5$![]() , for $p>5$
, for $p>5$![]() . However, its proof applies to any thin Lie algebra $L$
. However, its proof applies to any thin Lie algebra $L$![]() with second diamond $L_5$
with second diamond $L_5$![]() , for $p>5$
, for $p>5$![]() or $p=0$
or $p=0$![]() . A construction for that thin Lie algebra $L$
. A construction for that thin Lie algebra $L$![]() was also given in [Reference Caranti, Mattarei, Newman and Scoppola13], and that is valid in every characteristic except for characteristic two. The diamonds of $L$
was also given in [Reference Caranti, Mattarei, Newman and Scoppola13], and that is valid in every characteristic except for characteristic two. The diamonds of $L$![]() occur in each degree congruent to $\pm 1$
occur in each degree congruent to $\pm 1$![]() modulo $6$
modulo $6$![]() , and so as noted above one has $[L_{i-1}yy]\neq 0$
, and so as noted above one has $[L_{i-1}yy]\neq 0$![]() for each $i$
for each $i$![]() multiple of six. Uniqueness of $L$
multiple of six. Uniqueness of $L$![]() fails in characteristic three because $5=2q-1$
fails in characteristic three because $5=2q-1$![]() with $q=3$
with $q=3$![]() , and in characteristic five because we may have $5=q$
, and in characteristic five because we may have $5=q$![]() then, and so lots of other thin Lie algebras enter those cases (see Remark 12).
then, and so lots of other thin Lie algebras enter those cases (see Remark 12).
Our next remark describes how in characteristic three one can produce uncountably many thin Lie algebras with $\dim (L_3)=1$![]() having several diamonds at distance two.
having several diamonds at distance two.
Remark 9 According to [Reference Caranti, Mattarei and Newman14, Section 9], for each power $q$![]() of the (positive) characteristic, there are uncountably many infinite-dimensional graded Lie algebras of maximal class $M$
of the (positive) characteristic, there are uncountably many infinite-dimensional graded Lie algebras of maximal class $M$![]() with precisely two distinct two-step centralizers and constituent sequence beginning with $2q,\,q,\,q$
with precisely two distinct two-step centralizers and constituent sequence beginning with $2q,\,q,\,q$![]() . As shown in [Reference Caranti and Mattarei9, Section 5], each such $M$
. As shown in [Reference Caranti and Mattarei9, Section 5], each such $M$![]() has a maximal subalgebra $L$
has a maximal subalgebra $L$![]() which becomes thin under a new grading, and its diamonds start with $L_1,\,L_{2q-1},\,L_{3q-2},\,L_{4q-3}$
which becomes thin under a new grading, and its diamonds start with $L_1,\,L_{2q-1},\,L_{3q-2},\,L_{4q-3}$![]() . In characteristic three and taking $q=3$
. In characteristic three and taking $q=3$![]() those diamonds are $L_1,\,L_5,\,L_7,\,L_9$
those diamonds are $L_1,\,L_5,\,L_7,\,L_9$![]() . Consequently, $[L_5yy]\neq 0$
. Consequently, $[L_5yy]\neq 0$![]() and $[L_7yy]\neq 0$
and $[L_7yy]\neq 0$![]() .
.
The thin Lie algebras of the above remarks suggest that we might be able to obtain more information on the earliest diamond $L_j$![]() with $[L_jyy]\neq 0$
with $[L_jyy]\neq 0$![]() than on an arbitrary one, hence we will do that in preparation for a proof of Theorem 11.
than on an arbitrary one, hence we will do that in preparation for a proof of Theorem 11.
Lemma 10 Let $L$![]() be a thin Lie algebra with $\dim (L_3)=1,$
be a thin Lie algebra with $\dim (L_3)=1,$![]() and let $y$
and let $y$![]() span $C_{L_1}(L_2)$
span $C_{L_1}(L_2)$![]() . Suppose $[Lyy]\neq 0$
. Suppose $[Lyy]\neq 0$![]() , and let $j$
, and let $j$![]() be minimal such $[L_jyy]\neq 0$
be minimal such $[L_jyy]\neq 0$![]() . Then $L_{j-2}$
. Then $L_{j-2}$![]() and $L_{j-3}$
and $L_{j-3}$![]() are one-dimensional and centralized by $y$
are one-dimensional and centralized by $y$![]() .
.
Proof. According to Lemma 7, we have $\dim (L_j)=2$![]() , and hence $\dim (L_{j-1})=1$
, and hence $\dim (L_{j-1})=1$![]() because of Corollary 5. Note that $j>3$
because of Corollary 5. Note that $j>3$![]() . Let $t$
. Let $t$![]() be any non-zero element of $L_{j-3}$
be any non-zero element of $L_{j-3}$![]() . Then $[tyy]=0$
. Then $[tyy]=0$![]() and $[txyy]=0$
and $[txyy]=0$![]() by minimality of $j$
by minimality of $j$![]() , and hence
, and hence
Because of Proposition 2, we are not in characteristic two, and so we conclude $[tyxy]=0$![]() . But then $[tyx]=0$
. But then $[tyx]=0$![]() , because $L_{j-1}$
, because $L_{j-1}$![]() contains no non-zero element centralized by $y$
contains no non-zero element centralized by $y$![]() . The covering property now implies $[ty]=0$
. The covering property now implies $[ty]=0$![]() , otherwise $[tyx]$
, otherwise $[tyx]$![]() and $[tyy]$
and $[tyy]$![]() , which both vanish, would have to span $L_{j-1}$
, which both vanish, would have to span $L_{j-1}$![]() . Because $t$
. Because $t$![]() was an arbitrary non-zero element of $L_{j-3}$
was an arbitrary non-zero element of $L_{j-3}$![]() , Corollary 5 implies $\dim (L_{j-3})=1$
, Corollary 5 implies $\dim (L_{j-3})=1$![]() . Finally, $L_{j-2}$
. Finally, $L_{j-2}$![]() has dimension one because it is spanned by $[tx]$
has dimension one because it is spanned by $[tx]$![]() . But we know that $L_{j-2}$
. But we know that $L_{j-2}$![]() contains a non-zero element centralized by $y$
contains a non-zero element centralized by $y$![]() , and hence $[L_{j-2}y]=0$
, and hence $[L_{j-2}y]=0$![]() .
.
We are ready to prove the harder analogue of Proposition 2 for odd characteristics, thus completing a proof of Theorem 1. As our discussion leading to Remark 8 shows, we need an additional assumption to ensure that no diamonds occur at distance two. As it turns out, assuming $\dim (L_5)=1$![]() will do, which is another way of asking that the second diamond of $L$
will do, which is another way of asking that the second diamond of $L$![]() occurs past $L_5$
occurs past $L_5$![]() .
.
Theorem 11 Let $L$![]() be a thin Lie algebra of odd characteristic, with $\dim (L_3)=\dim (L_5)=1,$
be a thin Lie algebra of odd characteristic, with $\dim (L_3)=\dim (L_5)=1,$![]() and let $y$
and let $y$![]() span $C_{L_1}(L_2)$
span $C_{L_1}(L_2)$![]() . Then $[Lyy]=0$
. Then $[Lyy]=0$![]() .
.
Proof. Besides the relation $[yxy]=0$![]() , which serves to define $y$
, which serves to define $y$![]() up to scalar multiples, in $L$
up to scalar multiples, in $L$![]() we also have $[yxxy]=0$
we also have $[yxxy]=0$![]() and $[yxxxy]=0$
and $[yxxxy]=0$![]() . In fact, the former claim follows from $0=[yx[yx]]=[yxyx]-[yxxy]=-[yxxy]$
. In fact, the former claim follows from $0=[yx[yx]]=[yxyx]-[yxxy]=-[yxxy]$![]() . As a consequence, $[yxxx]$
. As a consequence, $[yxxx]$![]() spans $L_4$
spans $L_4$![]() . To prove the latter claim, assuming $[yxxxy]\neq 0$
. To prove the latter claim, assuming $[yxxxy]\neq 0$![]() for a contradiction, it will span $L_5$
for a contradiction, it will span $L_5$![]() because of our hypothesis $\dim (L_5)=1$
because of our hypothesis $\dim (L_5)=1$![]() . Then because $0=[yxx[xyy]]=[yxxxyy]-2[yxxyxy]+[yxxyyx]=[yxxxyy]$
. Then because $0=[yxx[xyy]]=[yxxxyy]-2[yxxyxy]+[yxxyyx]=[yxxxyy]$![]() , we find $[L_5y]=0$
, we find $[L_5y]=0$![]() . Consequently, $[yxxxyx]$
. Consequently, $[yxxxyx]$![]() spans $L_6$
spans $L_6$![]() , and we also have $[yxxxxy]=0$
, and we also have $[yxxxxy]=0$![]() . By combining these two facts and computing $0=[yxxxxy]=-[y[yxxxx]]=4[yxxxyx]$
. By combining these two facts and computing $0=[yxxxxy]=-[y[yxxxx]]=4[yxxxyx]$![]() , we obtain the desired contradiction.
, we obtain the desired contradiction.
Now suppose for a contradiction that $[Lyy]\neq 0$![]() , and let $j$
, and let $j$![]() be minimal such that $[L_jyy]\neq 0$
be minimal such that $[L_jyy]\neq 0$![]() . We will use the equations $[yxxy]=0$
. We will use the equations $[yxxy]=0$![]() and $[yxxxy]=0$
and $[yxxxy]=0$![]() to obtain a contradiction. Let $t$
to obtain a contradiction. Let $t$![]() be a non-zero element of $L_{j-3}$
be a non-zero element of $L_{j-3}$![]() . According to Lemma 7 we have $[ty]=0$
. According to Lemma 7 we have $[ty]=0$![]() and $[txy]=0$
and $[txy]=0$![]() , and $L_{j-1}$
, and $L_{j-1}$![]() is spanned by $v:=[txx]$
is spanned by $v:=[txx]$![]() . Furthermore, $\dim (L_j)=2$
. Furthermore, $\dim (L_j)=2$![]() , and hence $[vyy]=0$
, and hence $[vyy]=0$![]() according to Corollary 5. The calculations
according to Corollary 5. The calculations
and
taken together imply $[vxyy]=[vyxy]=0$![]() . Because $[vx]$
. Because $[vx]$![]() and $[vy]$
and $[vy]$![]() span $L_j$
span $L_j$![]() , we obtain $[L_jyy]=0$
, we obtain $[L_jyy]=0$![]() , which provides the desired contradiction.
, which provides the desired contradiction.
We discuss the extent to which hypothesis $\dim (L_5)=1$![]() of Theorem 11 is necessary. As we recalled in Remark 8, over a field of characteristic $p>5$
of Theorem 11 is necessary. As we recalled in Remark 8, over a field of characteristic $p>5$![]() that hypothesis serves to exclude a single exception, given by the unique thin Lie algebra with second diamond $L_5$
that hypothesis serves to exclude a single exception, given by the unique thin Lie algebra with second diamond $L_5$![]() , identified in [Reference Caranti, Mattarei, Newman and Scoppola13, Theorem 2(a)] and described in Remark 8. However, if we omit the hypothesis $\dim (L_5)=1$
, identified in [Reference Caranti, Mattarei, Newman and Scoppola13, Theorem 2(a)] and described in Remark 8. However, if we omit the hypothesis $\dim (L_5)=1$![]() of Theorem 11 in characteristic $p=3$
of Theorem 11 in characteristic $p=3$![]() , its conclusion $[Lyy]=0$
, its conclusion $[Lyy]=0$![]() is violated by uncountably many thin Lie algebras with second diamond $L_5$
is violated by uncountably many thin Lie algebras with second diamond $L_5$![]() and third diamond $L_7$
and third diamond $L_7$![]() , which we described in Remark 9. The following remark focuses on the borderline case $p=5$
, which we described in Remark 9. The following remark focuses on the borderline case $p=5$![]() .
.
Remark 12 We discuss how far Theorem 11 may be extended to include thin Lie algebras of characteristic five, with second diamond $L_5$![]() and an additional assumption. Countably many thin Lie algebras with second diamond $L_q$
and an additional assumption. Countably many thin Lie algebras with second diamond $L_q$![]() were constructed in [Reference Avitabile and Mattarei4], for any power $q$
were constructed in [Reference Avitabile and Mattarei4], for any power $q$![]() of the odd characteristic. In particular, when $q=5$
of the odd characteristic. In particular, when $q=5$![]() , this gives us a countable family of thin Lie algebras with second diamond $L_5$
, this gives us a countable family of thin Lie algebras with second diamond $L_5$![]() . However, all those thin Lie algebras, which have third diamond $L_{2q-1}=L_9$
. However, all those thin Lie algebras, which have third diamond $L_{2q-1}=L_9$![]() (possibly fake, see Remark 13 below), do satisfy the conclusion $[Lyy]=0$
(possibly fake, see Remark 13 below), do satisfy the conclusion $[Lyy]=0$![]() of Theorem 11.
of Theorem 11.
In fact, one can prove that $[Lyy]=0$![]() holds for any thin Lie algebra $L$
holds for any thin Lie algebra $L$![]() of characteristic five satisfying $\dim (L_3)=1$
of characteristic five satisfying $\dim (L_3)=1$![]() , $\dim (L_5)=2$
, $\dim (L_5)=2$![]() , and $[L_7y]=0$
, and $[L_7y]=0$![]() . (Here the hypothesis $[L_7y]=0$
. (Here the hypothesis $[L_7y]=0$![]() implies that neither $L_7$
implies that neither $L_7$![]() nor $L_8$
nor $L_8$![]() is a diamond, and hence the third diamond of $L$
is a diamond, and hence the third diamond of $L$![]() does not occur earlier than $L_9$
does not occur earlier than $L_9$![]() .) A proof of this fact follows the general inductive strategy employed in [Reference Avitabile and Mattarei2], but is not a formal consequence of results stated in [Reference Avitabile and Mattarei2], where some generality was sacrificed in favour of a simpler exposition. In fact, part of that simplification in [Reference Avitabile and Mattarei2] relies on using our Theorem 11.
.) A proof of this fact follows the general inductive strategy employed in [Reference Avitabile and Mattarei2], but is not a formal consequence of results stated in [Reference Avitabile and Mattarei2], where some generality was sacrificed in favour of a simpler exposition. In fact, part of that simplification in [Reference Avitabile and Mattarei2] relies on using our Theorem 11.
Remark 13 We mentioned fake diamonds a couple of times in this section, in marginal comments to our main discussion. When assigning types to diamonds of a thin Lie algebra $L$![]() with second diamond $L_q$
with second diamond $L_q$![]() (see [Reference Caranti and Mattarei10]) or $L_{2q-1}$
(see [Reference Caranti and Mattarei10]) or $L_{2q-1}$![]() (see [Reference Caranti and Mattarei9]), it is convenient for descriptive purposes to allow certain one-dimensional homogeneous components to be called fake diamonds (of type $0$
(see [Reference Caranti and Mattarei9]), it is convenient for descriptive purposes to allow certain one-dimensional homogeneous components to be called fake diamonds (of type $0$![]() or $1$
or $1$![]() in the former case, and of type $0$
in the former case, and of type $0$![]() in the latter). In some situations, it may even make sense to allow the second diamond of $L$
in the latter). In some situations, it may even make sense to allow the second diamond of $L$![]() to be fake; this may, in fact, be viewed as the source of serious complications in characteristic two, see [Reference Avitabile and Mattarei4, Remarks 3.6 and 5.3], and [Reference Avitabile, Jurman and Mattarei7] for their resolution. For the avoidance of doubt, each reference to unqualified diamonds of a thin Lie algebra in the present paper is to genuine diamonds, that is, two-dimensional homogeneous components.
to be fake; this may, in fact, be viewed as the source of serious complications in characteristic two, see [Reference Avitabile and Mattarei4, Remarks 3.6 and 5.3], and [Reference Avitabile, Jurman and Mattarei7] for their resolution. For the avoidance of doubt, each reference to unqualified diamonds of a thin Lie algebra in the present paper is to genuine diamonds, that is, two-dimensional homogeneous components.
3. Thin loop algebras and the sandwich element
We conclude this paper with a discussion of the significance for thin Lie algebras of an important property of sandwich elements. Classical simple Lie algebras do not have sandwich elements, see [Reference Seligman21, p. 124]. By contrast, confirming a conjecture of Kostrikin, Premet proved in [Reference Premet19] that every finite-dimensional simple Lie algebra, over an algebraically closed field of characteristic $p>5$![]() , which is not classical, must have sandwich elements (that is, have strong degeneration).
, which is not classical, must have sandwich elements (that is, have strong degeneration).
The connection of this characterization of classical Lie algebras with (infinite-dimensional) thin Lie algebras comes from the fact that several of the latter have been constructed as loop algebras of certain finite-dimensional simple Lie algebras, or close to simple. In the simplest setting, one starts from a finite-dimensional simple Lie algebra $S$![]() over a field $F$
over a field $F$![]() , with a cyclic grading $S=\bigoplus _{k\in \mathbb {Z}/N\mathbb {Z}} S_k$
, with a cyclic grading $S=\bigoplus _{k\in \mathbb {Z}/N\mathbb {Z}} S_k$![]() , and considers the Lie algebra $S\otimes F[t]$
, and considers the Lie algebra $S\otimes F[t]$![]() over $F$
over $F$![]() , where $t$
, where $t$![]() is an indeterminate. Its subalgebra $L=\bigoplus _{k>0}S_{\bar k}\otimes t^{k}$
is an indeterminate. Its subalgebra $L=\bigoplus _{k>0}S_{\bar k}\otimes t^{k}$![]() , where $\bar k=k+N\mathbb {Z}$
, where $\bar k=k+N\mathbb {Z}$![]() , is naturally graded over the positive integers, and is called a loop algebra in this context. In certain cases, one needs a slightly more general construction involving also a derivation of $S$
, is naturally graded over the positive integers, and is called a loop algebra in this context. In certain cases, one needs a slightly more general construction involving also a derivation of $S$![]() (such as that of [Reference Avitabile and Mattarei4, Definition 2.1]), but that is inconsequential for our present observation.
(such as that of [Reference Avitabile and Mattarei4, Definition 2.1]), but that is inconsequential for our present observation.
It was proved in [Reference Caranti, Mattarei, Newman and Scoppola13] that a thin Lie algebra $L$![]() (of characteristic not $2$
(of characteristic not $2$![]() or $3$
or $3$![]() ) having second diamond $L_3$
) having second diamond $L_3$![]() and $\dim (L_4)=1$
and $\dim (L_4)=1$![]() belongs to one of (up to) two isomorphism types, and a thin Lie algebra $L$
belongs to one of (up to) two isomorphism types, and a thin Lie algebra $L$![]() (of characteristic not $2$
(of characteristic not $2$![]() , $3$
, $3$![]() or $5$
or $5$![]() ) with second diamond $L_5$
) with second diamond $L_5$![]() is unique up to isomorphism (see also Remark 8). Each of those thin Lie algebras can be realized as a loop algebra of a classical simple Lie algebra of type $A_1$
is unique up to isomorphism (see also Remark 8). Each of those thin Lie algebras can be realized as a loop algebra of a classical simple Lie algebra of type $A_1$![]() or $A_2$
or $A_2$![]() .
.
Now, the fact that those thin Lie algebras of [Reference Caranti, Mattarei, Newman and Scoppola13] are loop algebras of classical simple Lie algebras implies that there cannot be any non-zero element $y\in L_{\bar 1}$![]() with $(\operatorname {ad} y)^{2}=0$
with $(\operatorname {ad} y)^{2}=0$![]() , because such $y$
, because such $y$![]() would have the form $y=c\otimes t$
would have the form $y=c\otimes t$![]() for some sandwich element $c$
for some sandwich element $c$![]() of $S$
of $S$![]() , which cannot exist. For the same reason, if a thin Lie algebra $L$
, which cannot exist. For the same reason, if a thin Lie algebra $L$![]() (say of characteristic $p>5$
(say of characteristic $p>5$![]() ) with second diamond past $L_5$
) with second diamond past $L_5$![]() is a loop algebra of a simple Lie algebra $S$
is a loop algebra of a simple Lie algebra $S$![]() , then $S$
, then $S$![]() cannot be classical, because $L$
cannot be classical, because $L$![]() has a sandwich element $y$
has a sandwich element $y$![]() according to Theorem 11, and hence so does $S$
according to Theorem 11, and hence so does $S$![]() .
.
In fact, all constructions of thin Lie algebras with second diamond $q$![]() or $2q-1$
or $2q-1$![]() as loop algebras which were given in several papers [Reference Avitabile and Mattarei3–Reference Avitabile and Mattarei5, Reference Caranti8, Reference Caranti and Mattarei11] start from non-classical simple Lie algebras of various types. The occurrence of non-classical simple Lie algebras in those constructions was hardly surprising in itself, because the expected structure of such thin Lie algebras $L$
as loop algebras which were given in several papers [Reference Avitabile and Mattarei3–Reference Avitabile and Mattarei5, Reference Caranti8, Reference Caranti and Mattarei11] start from non-classical simple Lie algebras of various types. The occurrence of non-classical simple Lie algebras in those constructions was hardly surprising in itself, because the expected structure of such thin Lie algebras $L$![]() given by corresponding uniqueness results showed that the dimension of $S$
given by corresponding uniqueness results showed that the dimension of $S$![]() ought to be a power of $p$
ought to be a power of $p$![]() or one or two less in the various cases. However, the sandwich element $y$
or one or two less in the various cases. However, the sandwich element $y$![]() did provide guidance in identifying the appropriate cyclic grading of $S$
did provide guidance in identifying the appropriate cyclic grading of $S$![]() employed in those constructions.
employed in those constructions.
Competing interests
The author declares none.