Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
McBride, Adam C.
1977.
A theory of fractional integration for generalised functions II.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 77,
Issue. 3-4,
p.
335.
Tsalyuk, Z. B.
1979.
Volterra integral equations.
Journal of Soviet Mathematics,
Vol. 12,
Issue. 6,
p.
715.
Mcbride, Adam C.
1986.
Fractional powers of a class of mellin multiplier transforms part iii.
Applicable Analysis,
Vol. 21,
Issue. 1-2,
p.
151.
Kilbas, Anatoly A.
Saigo, Megumi
and
Shlapakov, Sergei A.
1993.
Integral transforms with fox'sH-function in spaces of summable functions.
Integral Transforms and Special Functions,
Vol. 1,
Issue. 2,
p.
87.
Raina, R. K.
Srivastava, H. M.
Kilbas, A. A.
and
Saigo, M.
2001.
Solvability of some Abel-type integral equations involving the Gauss hypergeometric function as kernels in the spaces of summable functions.
The ANZIAM Journal,
Vol. 43,
Issue. 2,
p.
291.


 of generalised functions. For 1≦
of generalised functions. For 1≦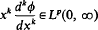 for each
for each