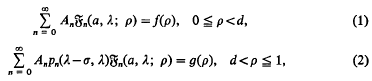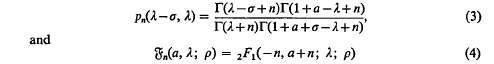Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Srivastava, H.M.
and
Panda, Rekha
1978.
A certain class of dual equations involving series of Jacobi and Laguerre polynomials.
Indagationes Mathematicae (Proceedings),
Vol. 81,
Issue. 1,
p.
502.
2001.
Canonical Problems in Scattering and Potential Theory Part 1.
Vol. 122,
Issue. ,