Article contents
Weighted Estimates for Solutions of the General Sturm-Liouville Equation and the Everitt-Giertz Problem. I
Published online by Cambridge University Press: 21 July 2014
Abstract
Consider the equation
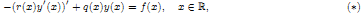
where ƒ ∈ Lp(ℝ), p ∈ (1, ∞) and
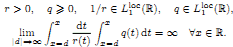
By a solution of (*), we mean any function y absolutely continuous together with (ry′) and satisfying (*) almost everywhere on ℝ. In addition, we assume that (*) is correctly solvable in the space Lp(ℝ), i.e.
(1) for any function 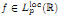 , there exists a unique solution y ∈ Lp(ℝ) of (*);
, there exists a unique solution y ∈ Lp(ℝ) of (*);
(2) there exists an absolute constant c1(p) > 0 such that the solution y ∈ Lp(ℝ) of (*) satisfies the inequality
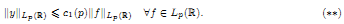
We study the following problem on the strengthening estimate (**). Let a non-negative function 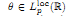 be given. We have to find minimal additional restrictions for θ under which the following inequality holds:
be given. We have to find minimal additional restrictions for θ under which the following inequality holds:
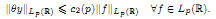
Here, y is a solution of (*) from the class Lp(ℝ), and c2 (p) is an absolute positive constant.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 58 , Issue 1 , February 2015 , pp. 125 - 147
- Copyright
- Copyright © Edinburgh Mathematical Society 2015
References
- 2
- Cited by


