Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bonanno, Gabriele
and
Livrea, Roberto
2003.
Multiplicity theorems for the Dirichlet problem involving the p-Laplacian.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 54,
Issue. 1,
p.
1.
Obersnel, Franco
and
Omari, Pierpaolo
2006.
Positive solutions of elliptic problems with locally oscillating nonlinearities.
Journal of Mathematical Analysis and Applications,
Vol. 323,
Issue. 2,
p.
913.
Motreanu, D.
Motreanu, V. V.
and
Papageorgiou, N. S.
2007.
A degree theoretic approach for multiple solutions of constant sign for nonlinear elliptic equations.
manuscripta mathematica,
Vol. 124,
Issue. 4,
p.
507.
Kristály, Alexandru
Moroşanu, Gheorghe
and
Tersian, Stepan
2007.
Quasilinear elliptic problems in RN involving oscillatory nonlinearities.
Journal of Differential Equations,
Vol. 235,
Issue. 2,
p.
366.
Afrouzi, G.A.
and
Heidarkhani, S.
2007.
Three solutions for a Dirichlet boundary value problem involving the -Laplacian.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 66,
Issue. 10,
p.
2281.
Anello, Giovanni
and
Cordaro, Giuseppe
2007.
Perturbation from Dirichlet problem involving oscillating nonlinearities.
Journal of Differential Equations,
Vol. 234,
Issue. 1,
p.
80.
Filippakis, Michael E.
and
Papageorgiou, Nikolaos S.
2008.
Multiple constant sign and nodal solutions for nonlinear elliptic equations with the p-Laplacian.
Journal of Differential Equations,
Vol. 245,
Issue. 7,
p.
1883.
Afrouzi, G.A.
and
Heidarkhani, S.
2008.
Three solutions for a quasilinear boundary value problem.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 69,
Issue. 10,
p.
3330.
He, Xiaoming
and
Zou, Wenming
2009.
Infinitely many positive solutions for Kirchhoff-type problems.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 70,
Issue. 3,
p.
1407.
Afrouzi, G.A.
and
Heidarkhani, S.
2009.
Existence of three solutions for a class of Dirichlet quasilinear elliptic systems involving the (p1,…,pn) -Laplacian.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 70,
Issue. 1,
p.
135.
Wang, Libo
and
Ge, Weigao
2009.
Infinitely many positive solutions of a singular dirichlet problem involving the p-Laplacian.
Communications in Nonlinear Science and Numerical Simulation,
Vol. 14,
Issue. 11,
p.
3784.
Afrouzi, G. A.
and
Heidarkhani, S.
2010.
Multiplicity results for a two-point boundary value double eigenvalue problem.
Ricerche di Matematica,
Vol. 59,
Issue. 1,
p.
39.
Heidarkhani, Shapour
and
Tian, Yu
2010.
Multiplicity results for a class of gradient systems depending on two parameters.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 73,
Issue. 2,
p.
547.
Wang, Libo
Ge, Weigao
and
Pei, Minghe
2010.
Infinitely many solutions of a second-order p-Laplacian problem with impulsive condition.
Applications of Mathematics,
Vol. 55,
Issue. 5,
p.
405.
Kristály, Alexandru
2010.
On singular elliptic equations involving oscillatory terms.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 72,
Issue. 3-4,
p.
1561.
Afrouzi, G.A.
and
Heidarkhani, S.
2010.
Multiplicity theorems for a class of Dirichlet quasilinear elliptic systems involving the -Laplacian.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 73,
Issue. 8,
p.
2594.
Wang, Libo
and
Pei, Minghe
2011.
Infinitely many solutions of a Sturm-Liouville system with impulses.
Journal of Applied Mathematics and Computing,
Vol. 35,
Issue. 1-2,
p.
577.
D’Aguì, Giuseppina
and
Sciammetta, Angela
2012.
Infinitely many solutions to elliptic problems with variable exponent and nonhomogeneous Neumann conditions.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 75,
Issue. 14,
p.
5612.
Han, Qi
2015.
Infinitely many positive harmonic functions with an oscillating boundary condition on exterior regions.
Complex Variables and Elliptic Equations,
Vol. 60,
Issue. 8,
p.
1106.
Faraci, Francesca
and
Farkas, Csaba
2016.
New Conditions for the Existence of Infinitely Many Solutions for a Quasi-Linear Problem.
Proceedings of the Edinburgh Mathematical Society,
Vol. 59,
Issue. 3,
p.
655.
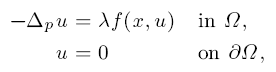 where Ω ∈ RN is a bounded open set with sufficiently smooth boundary ∂Ω, p > 1, λ > 0, and f: Ω × R → R is a Carathéodory function satisfying the following condition: there exists t̄ > 0 such that
where Ω ∈ RN is a bounded open set with sufficiently smooth boundary ∂Ω, p > 1, λ > 0, and f: Ω × R → R is a Carathéodory function satisfying the following condition: there exists t̄ > 0 such that
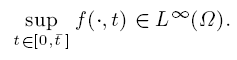 Precisely, our result ensures the existence of a sequence of a.e. positive weak solutions to the above problem, converging to zero in L∞(Ω).
Precisely, our result ensures the existence of a sequence of a.e. positive weak solutions to the above problem, converging to zero in L∞(Ω).