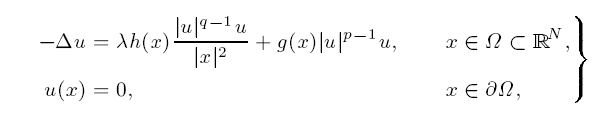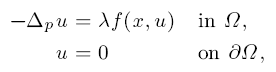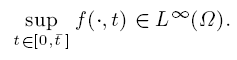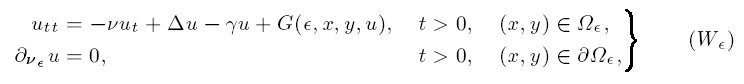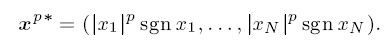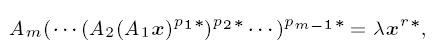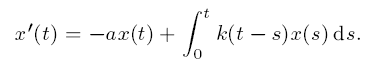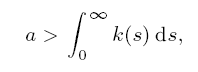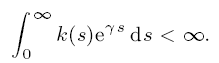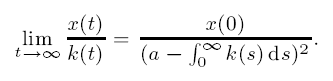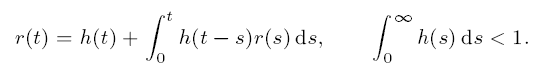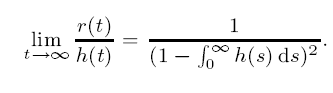Research Article
On subhereditary radicals and reduced rings
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 255-266
-
- Article
- Export citation
Some results for semilinear elliptic equations with critical potential
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1-24
-
- Article
- Export citation
Infinitely many arbitrarily small positive solutions for the Dirichlet problem involving the p-Laplacian
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 511-519
-
- Article
- Export citation
Existence and non-existence of the first eigenvalue of the perturbed Hardy–Sobolev operator
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1021-1043
-
- Article
- Export citation
Almost-periodic solutions of elliptic and parabolic equations in unbounded domains
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1275-1306
-
- Article
- Export citation
On convergence, admissibility and attractors for damped wave equations on squeezed domains
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 765-791
-
- Article
- Export citation
Quasiregular mappings and Young measures
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1045-1056
-
- Article
- Export citation
Conditional persistence in logistic models via nonlinear diffusion
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 267-281
-
- Article
- Export citation
A priori estimates for solutions to elliptic equations on non-smooth domains
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 793-813
-
- Article
- Export citation
Nonlinear eigenvalue–eigenvector problems for STP matrices
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1307-1331
-
- Article
- Export citation
Subexponential solutions of linear integro-differential equations and transient renewal equations
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 521-543
-
- Article
- Export citation
Existence and non-existence of the first eigenvalue of the perturbed Hardy–Sobolev operator
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1021-1043
-
- Article
- Export citation
Hardy spaces on ZN
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 25-43
-
- Article
- Export citation
Some fine properties of currents and applications to distributional Jacobians
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 815-842
-
- Article
- Export citation
Explicit Wiener–Hopf factorization and nonlinear Riemann–Hilbert problems
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 45-74
-
- Article
- Export citation
Nonlinear eigenvalue problems for a class of ordinary differential equations
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1333-1359
-
- Article
- Export citation
Convergence theorems for intermediate problems. II
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1057-1072
-
- Article
- Export citation
A derivation theory for generalized Besicovitch spaces and its application for partial differential equations
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 283-315
-
- Article
- Export citation
Diffusive-dispersive travelling waves and kinetic relations. II A hyperbolic–elliptic model of phase-transition dynamics
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 545-565
-
- Article
- Export citation
Quasiregular mappings and Young measures
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1045-1056
-
- Article
- Export citation