Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-13T10:44:56.198Z Has data issue: false hasContentIssue false
  • English
  • Français

On some nonlinear Schrödinger equations in ℝN

Part of: Elliptic equations and systems Partial differential equations

Published online by Cambridge University Press:  23 August 2022

Juncheng Wei  and
Yuanze Wu Open the ORCID record for Yuanze Wu [Opens in a new window]
Juncheng Wei
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, B.C., Canada V6T 1Z2 (jcwei@math.ubc.ca)
Yuanze Wu
Affiliation:
School of Mathematics, China University of Mining and Technology, Xuzhou, 221116, P.R. China (wuyz850306@cumt.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we consider the following nonlinear Schrödinger equations with the critical Sobolev exponent and mixed nonlinearities: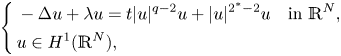

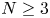\[\left\{\begin{aligned} & -\Delta u+\lambda u=t|u|^{q-2}u+|u|^{2^{*}-2}u\quad\text{in }\mathbb{R}^{N},\\ & u\in H^{1}(\mathbb{R}^{N}), \end{aligned}\right.\]
where $N\geq 3$, $t>0$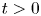, $\lambda >0$ 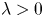and $2< q<2^{*}=\frac {2N}{N-2}$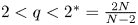. Based on our recent study on the normalized solutions of the above equation in [J. Wei and Y. Wu, Normalized solutions for Schrodinger equations with critical Sobolev exponent and mixed nonlinearities, e-print arXiv:2102.04030[Math.AP].], we prove that

  1. (1) the above equation has two positive radial solutions for $N=3$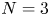, $2< q<4$ 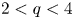and $t>0$ 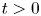sufficiently large, which gives a rigorous proof of the numerical conjecture in [J. Dávila, M. del Pino and I. Guerra. Non-uniqueness of positive ground states of non-linear Schrödinger equations. Proc. Lond. Math. Soc. 106 (2013), 318–344.];

  2. (2) there exists $t_q^{*}>0$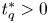 for $2< q\leq 4$ 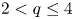such that the above equation has ground-states for $t\geq t_q^{*}$ 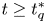in the case of $2< q<4$ 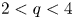and for $t>t_4^{*}$ 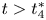in the case of $q=4$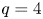, while the above equation has no ground-states for $0< t< t_q^{*}$ 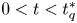for all $2< q\leq 4$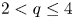, which, together with the well-known results on ground-states of the above equation, almost completely solve the existence of ground-states, except for $N=3$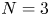, $q=4$ 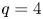and $t=t_4^{*}$.

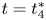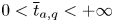Moreover, based on the almost completed study on ground-states to the above equation, we introduce a new argument to study the normalized solutions of the above equation to prove that there exists $0<\overline {t}_{a,q}<+\infty$ for $2< q<2+\frac {4}{N}$ 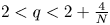such that the above equation has no positive normalized solutions for $t>\overline {t}_{a,q}$ 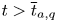with $\int _{\mathbb {R}^{N}}|u|^{2}{\rm d}x=a^{2}$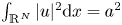, which, together with our recent study in [J. Wei and Y. Wu, Normalized solutions for Schrodinger equations with critical Sobolev exponent and mixed nonlinearities, e-print arXiv:2102.04030[Math.AP].], gives a completed answer to the open question proposed by Soave in [N. Soave. Normalized ground states for the NLS equation with combined nonlinearities: The Sobolev critical case. J. Funct. Anal. 279 (2020) 108610.]. Finally, as applications of our new argument, we also study the following Schrödinger equation with a partial confinement: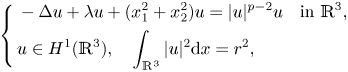
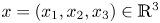\[\left\{ \begin{aligned} & -\Delta u+\lambda u+(x_1^{2}+x_2^{2})u=|u|^{p-2}u\quad\text{in }\mathbb{R}^{3},\\ & u\in H^{1}(\mathbb{R}^{3}),\quad \int_{\mathbb{R}^{3}}|u|^{2}{\rm d}x=r^{2}, \end{aligned}\right.\]
where $x=(x_1,x_2,x_3)\in \mathbb {R}^{3}$, $\frac {10}{3}< p<6$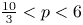, $r>0$ 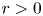is a constant and $(u, \lambda )$ 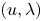is a pair of unknowns with $\lambda$ 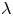being a Lagrange multiplier. We prove that the above equation has a second positive solution, which is also a mountain-pass solution, for $r>0$ 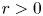sufficiently small. This gives a positive answer to the open question proposed by Bellazzini et al. in [J. Bellazzini, N. Boussaid, L. Jeanjean and N. Visciglia. Existence and Stability of Standing Waves for Supercritical NLS with a Partial Confinement. Commun. Math. Phys. 353 (2017), 229–251].

Keywords

Ground statenormalized solutionSchrödinger equationpower-type nonlinearity

MSC classification

Primary: 35B09: Positive solutions
Secondary: 35B33: Critical exponents 35B40: Asymptotic behavior of solutions 35J20: Variational methods for second-order elliptic equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 5 , October 2023 , pp. 1503 - 1528
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akahori, T., Ibrahim, S. and Kikuchi, H.. Linear instability and nondegeneracy of ground state for combined power-type nonlinear scalar field equations with the Sobolev critical exponent and large frequency parameter. Proc. Roy. Soc. Edinburgh Sect. A 150 (2020), 2417–2441.CrossRefGoogle Scholar
Akahori, T., Ibrahim, S., Kikuchi, H. and Nawa, H.. Existence of a ground state and blow-up problem for a nonlinear Schrödinger equation with critical growth. Differ. Integral Equ. 25 (2012), 383–402.Google Scholar
Akahori, T., Ibrahim, S., Kikuchi, H. and Nawa, H.. Global dynamics above the ground state energy for the combined power type nonlinear Schrodinger equations with energy critical growth at low frequencies, e-print arXiv:1510.08034[Math.AP](to appear in Memoirs of the AMS).Google Scholar
Akahori, T., Ibrahim, S., Ikoma, N., Kikuchi, H. and Nawa, H.. Uniqueness and nondegeneracy of ground states to nonlinear scalar field equations involving the Sobolev critical exponent in their nonlinearities for high frequencies. Calc. Var. PDEs 58 (2019), 120.CrossRefGoogle Scholar
Atkinson, F. and Peletier, L.. Emden-Fowler equations involving critical exponents. Nonlinear Anal. 10 (1986), 755–776.CrossRefGoogle Scholar
Alves, C. O., Souto, M. A. S. and Montenegro, M.. Existence of a ground state solution for a nonlinear scalar field equation with critical growth. Calc. Var. PDEs 43 (2012), 537–554.CrossRefGoogle Scholar
Bellazzini, J., Boussaid, N., Jeanjean, L. and Visciglia, N.. Existence and stability of standing waves for supercritical NLS with a partial confinement. Commun. Math. Phys. 353 (2017), 229–251.CrossRefGoogle Scholar
Berestycki, H. and Lions, P.-L.. Nonlinear scalar field equations. I: existence of a ground state. Arch. Ration. Mech. Anal. 82 (1983), 313–345.CrossRefGoogle Scholar
Brézis, H. and Nirenberg, L.. Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents. Commun. Pure Appl. Math. 36 (1983), 437–477.CrossRefGoogle Scholar
Chen, W., Dávila, J. and Guerra, I.. Bubble tower solutions for a supercritical elliptic problem in $\mathbb {R}^{N}$. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 15 (2016), 85–116.Google Scholar
Chen, Z. and Zou, W.. On the Brezís-Nirenberg problem in a ball. Differ. Integral Equ. 25 (2012), 527–542.Google Scholar
Coffman, C.. Uniqueness of the ground state solution for $\Delta u-u+u^{3}=0$ and a variational characterization of other solutions. Arch. Rational Mech. Anal. 46 (1972), 81–95.CrossRefGoogle Scholar
Coles, M. and Gustafson, S.. Solitary waves and dynamics for subcritical perturbations of energy critical NLS. Publ. Res. Inst. Math. Sci. 56 (2020), 647–699.CrossRefGoogle Scholar
Dávila, J., del Pino, M. and Guerra, I.. Non-uniqueness of positive ground states of non-linear Schrödinger equations. Proc. Lond. Math. Soc. 106 (2013), 318–344.CrossRefGoogle Scholar
Dovetta, S., Serra, E. and Tilli, P.. Action versus energy ground states in nonlinear Schrödinger equations, e-print arXiv:2107.08655v1[math.AP].Google Scholar
Ferrero, A. and Gazzola, F.. On subcriticality assumptions for the existence of ground states of quasilinear elliptic equations. Adv. Differ. Equ. 8 (2003), 1081–1106.Google Scholar
Gidas, B., Ni, W. and Nirenberg, L.. Symmetry of positive solutions of nonlinear elliptic equations in $\mathbb {R}^{N}$, in: L. Nachbin (Ed.), Math. Anal. Appl. Part A, Advances in Math. Suppl. Studies, Vol. 7A (Academic Press, 1981), pp. 369–402.Google Scholar
Gazzola, F. and Serrin, J.. Asymptotic behavior of ground states of quasilinear elliptic problems with two vanishing parameters. Ann. Inst. H. Poincaré Anal. Non Linéaire 19 (2002), 477–504.CrossRefGoogle Scholar
Jeanjean, L. and Le, T.. Multiple normalized solutions for a Sobolev critical Schrödinger equation. Math. Ann. (2021). DOI: 10.1007/s00208-021-02228-0Google Scholar
Jeanjean, L. and Lu, S.. On global minimizers for a mass constrained problem e-print arXiv:2108.04142v2[math.AP].Google Scholar
Knaap, M. and Peletier, L.. Quasilinear elliptic equations with nearly critical growth. Comm. PDEs 14 (1989), 1351–1383.CrossRefGoogle Scholar
Kwong, M.. Uniqueness of positive solution of $\Delta u-u+u^{p}=0$ in $\mathbf {R}^{N}$. Arch. Rational Mech. Anal. 105 (1989), 243–266.CrossRefGoogle Scholar
Lions, P. L.. The concentration-compactness principle in the calculus of variations. The locally compact case, part 2. Ann. Inst. H. Poincaré Anal. Non Linéaire 1 (1984), 223–283.CrossRefGoogle Scholar
Liu, J., Liao, J.-F. and Tang, C.-L.. Ground state solution for a class of Schrödinger equations involving general critical growth term. Nonlinearity 30 (2017), 899–911.CrossRefGoogle Scholar
Ma, S. and Moroz, V.. Asymptotic profiles for a nonlinear Schrödinger equation with critical combined powers nonlinearty, e-print arXiv2108.01421[Math.AP].Google Scholar
McLeod, K.. Uniqueness of positive radial solutions of $\Delta u+f(u)=0$ in $\mathbb {R}^{N}$. II. Trans. Amer. Math. Soc. 339 (1993), 495–505.Google Scholar
McLeod, K. and Serrin, J.. Uniqueness of positive radial solutions of $\Delta u+f(u)=0$ in $\mathbb {R}^{N}$. Arch. Ration. Mech. Anal. 99 (1987), 115–145.CrossRefGoogle Scholar
Peletier, L. and Serrin, J.. Uniqueness of positive solutions of semilinear equations in $\mathbb {R}^{N}$. Arch. Ration. Mech. Anal. 81 (1983), 181–197.CrossRefGoogle Scholar
Peletier, L. and Serrin, J.. Uniqueness of nonnegative solutions of semilinear equations in $\mathbb {R}^{N}$. J. Differ. Equ. 61 (1986), 380–397.CrossRefGoogle Scholar
Pucci, P. and Serrin, J.. Uniqueness of ground states for quasilinear elliptic operators. Indiana Univ. Math. J. 47 (1998), 501–528.Google Scholar
Serrin, J. and Tang, M.. Uniqueness of ground states for quasilinear elliptic equations. Indiana Univ. Math. J. 49 (2000), 897–923.CrossRefGoogle Scholar
Soave, N.. Normalized ground states for the NLS equation with combined nonlinearities: The Sobolev critical case. J. Funct. Anal. 279 (2020), 108610.CrossRefGoogle Scholar
Wei, J. and Wu, Y.. Normalized solutions for Schrodinger equations with critical Sobolev exponent and mixed nonlinearities. J. Funct. Anal. 283 (2022), 109574.CrossRefGoogle Scholar
Willem, M.. Minimax Theorems (Boston, Birkhäuser, 1996).CrossRefGoogle Scholar
Zhang, J. and Zou, W.. A Berestycki-Lions theorem revisited. Commun. Contemp. Math. 14 (2012), 1250033.CrossRefGoogle Scholar