Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bousselsal, M.
and
Chipot, M.
1995.
Relaxation of some functionals of the calculus of variations.
Archiv der Mathematik,
Vol. 65,
Issue. 4,
p.
316.
Yan, Baisheng
and
Zhou, Zhengfang
2001.
Lp-Mean coercivity, regularity and relaxation in the calculus of variations.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 46,
Issue. 6,
p.
835.
Martin, Robert J.
Voss, Jendrik
Ghiba, Ionel-Dumitrel
Sander, Oliver
and
Neff, Patrizio
2020.
The Quasiconvex Envelope of Conformally Invariant Planar Energy Functions in Isotropic Hyperelasticity.
Journal of Nonlinear Science,
Vol. 30,
Issue. 6,
p.
2885.


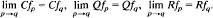 . This is the case for (
. This is the case for (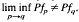 . In the last part of this work, we show that
. In the last part of this work, we show that 