Uniqueness of the solution to the following inverse problem is established. Given the heat equation, the initial temperature, the boundary regime at the left end of a finite rod and the measurements of the temperature at an intermediate point of the rod, find the temperature at the right end of the rod.

In this paper we consider the Stefan problem with a heating term. We study the continuity of the interfaces between the mush, the liquid and the solid for solutions of finite lapnumber.

Let ℐN denote the set of (N + 1)-tuples of C1 ω-periodic functions; the point P = (pN,…, p1p0) ϵ ℐN is identified with the differential equation

We examine the way in which the total number of ω-periodic solutions can vary as P traverses a path in ℐN.

We use a direct, geometric approach to study the free surface boundary conditions for stationary flows of viscous liquids. The free surface problem is characterised by a mapping on smooth variations of a given configuration; this mapping has a simple structure, which we determine by computing its differential, and studying it in terms of the space dimension and the surface tension coefficient. Applications are given to problems of existence, uniqueness and regularity in free surface flows.

We study a semilinear elliptic problem on ℝN where a potential is not a bounded function but can also be an infinite measure. We analyse the lack of compactness of the problem, obtaining a structure theorem for Palais-Smale sequences. This result allows us to obtain different kinds of existence theorems by a variational approach.

A systematic approach is proposed for the generalised factorisation of certain non-rational n × n matrix functions. The first main result consists in a transformation of a meromorphic into a generalised factorisation by algebraic means. It closes a gap between the classical Wiener-Hopf procedure and the operator theoretic method of generalised factorisation. Secondly, as examples we consider certain matrix functions of Jones form or of N-part form, which are equivalent to each other, in a sense. The factorisation procedure is complete and explicit, based only on the factorisation of scalar functions, of rational matrix functions and upon linear algebra. Applications in elastodynamic diffraction theory are treated in detail and in a most effective way.

We give a complete solution to the G-closure problem for mixtures of two well-ordered possibly anisotropic conductors. Both the G-closure with fixed volume fractions and the full G-closure are computed. The conductivity tensors are considered in a fixed frame and no rotations are allowed.

We study the initial growth of the interfaces of non-negative local solutions of the equation ut = (um)xx−λuq when m ≧ 1 and 0<q <1. We show that if with C < C0, for some explicit C0 = C0(λ, m, q), then the free boundary Ϛ(t) = sup {x:u(x, t) > 0} is a ‘heating front’. More precisely Ϛ(t) ≧at(m−q)/2(1−q) for any t small enough and for some a>0. If on the contrary, with C<C0, then Ϛ(t) is a ‘cooling front’ and in fact Ϛ(t) ≧ −atm−q)/2(1−q) for any t small enough and for some a > 0. Applications to solutions of the associated Cauchy and Dirichlet problems are also given.

The paper is concerned with equations of the form x' = A(t)x +f(t, x), where A is a continuous matrix function defined on ℝ, f is a continuous vector-valued function of (t, x) with f(t, 0) = 0. It is proved that if x' = A(t)x has an exponential trichotomy, A is bounded and f satisfies the Lipschitz condition with coefficient sufficiently small, then these equations are topologically equivalent to the systems of equations of the form , where B, g satisfy the same conditions as A, f.

We consider the question: when do two ordinary, linear, quasi-differential expressions commute? For classical differential expressions, answers to this question are well known. The set of all expressions which commute with a given such expression form a commutative ring. For quasi-differential expressions less is known and such an algebraiastructure can no longer be exploited. Using the theory of very general quasi-differential expressions with matrix-valued coefficients, we prove some general results concerning commutativity of such expressions. We show how, when specialised to scalar expressions, these results include a proof of the conjecture that if a 2nth-order scalar, J-symmetric (or real symmetric) quasi-differential expression commutes with a second order expression having the same properties, then the former must be an nth-order polynomial in the latter. This result was conjectured in a paper by Race and Zettl, to which this paper is a sequel.

This paper considers the Cauchy problem for the isentropic equations of gas dynamics in Euler coordinates ρt + (ρu)x = 0, (ρu)t + (ρu)2 + P(ρ))x=0 and gives the Hölder-continuous solution by applying the method of vanishing viscosity.

We give several results which extend our recent proof of the Payne-Pólya–Weinberger conjecture to ratios of higher eigenvalues. In particular, we show that for a bounded domain Ω⊂ℝn the eigenvalues of its Dirichlet Laplacian obey where λm denotes the mth eigenvalue and jp,k denotes the kth positive zero of the Bessel function Jp(x). Certain extensions of this result are given, the most general being the bound where k≧2 and l(m) denotes the number of nodal domains of an mth eigenfunction. Our results imply certain further conjectures of Payne, Pólya, and Weinberger concerning λ3/λ2 and λ4/λ3. In addition, we find a resonably good bound on λ4/λ1. We also briefly discuss extensions to Schrödinger operators and other elliptic eigenvalue problems.

This work is devoted to the study of subharmonic solutions of a second-order Hamiltonian system

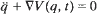
near an equilibrium point, say q = 0. The problem of existence of periodic solutions from the global point of view is also considered.

This problem has been studied for the case where the potential is positive and superquadratic. In this work a potential V that has change in sign is considered. The potential is decomposed as

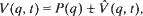
where P is homogeneous, superquadratic and nondegenerate, and 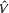is of higher order near 0. In this paper the existence is shown of a sequence of subharmonic solutions of the equation above that converges to the equilibrium, such that their minimal periods converge to infinity.

This problem is approached from a variational point of view. Existence of subharmonic and periodic solutions is obtained via minimax techniques.

We study the blow-up of positive solutions of the Cauchy problem for the semilinear parabolic equation

where u is a scalar function of the spatial variable x ∈ ℝN and time t > 0, a ∈ ℝV, a ≠ 0, 1 < p and 1 ≦ q. We show that: (a) if p > 1 and 1 ≦ q ≦ p, there always exist solutions which blow up in finite time; (b) if 1 < q ≦ p ≦ min {1 + 2/N, 1 + 2q/(N + 1)} or if q = 1 and 1 < p ≦ l + 2/N, then all positive solutions blow up in finite time; (c) if q > 1 and p > min {1 + 2/N, 1 + 2q/N + 1)}, then global solutions exist; (d) if q = 1 and p > 1 + 2/N, then global solutions exist.

In this paper we introduce a new tool in geometric measure theory and then we apply it to study the rank properties of the derivatives of vector functions with bounded variation.

Most of the convergence results appearing so far for delayed Lotka–Volterra-type systems require that undelayed negative feedback dominate both delayed feedback and interspecific interactions. Such a requirement is rarely met in real systems. In this paper we present convergence criteria for systems without instantaneous feedback. Roughly, our results suggest that in a Lotka–Volterra-type system if some of the delays are small, and initial functions are small and smooth, then the convergence of its positive steady state follows that of the undelayed system or the corresponding system whose instantaneous negative feedback dominates. In particular, we establish explicit expressions for allowable delay lengths for such convergence to sustain.

In this paper we establish bounds constraining the effective conductivity tensor of composites made of an arbitrary number n of possibly anisotropic phases in prescribed volume fractions. The bounds are valid in any spatial dimension d≧2. The bounds have a very simple and concise form and include those previously obtained by Hashin and Shtrikman, Murat and Tartar, Lurie and Cherkaev, Kohn and Milton, Avellaneda, Cherkaev, Lurie and Milton and Dell'Antonio and Nesi.

The behaviour of a microsensor thermistor is described by a system of nonlinear coupled elliptic equations subject to mixed Dirichlet-Neumann boundary conditions, to be solved on different domains. We employ the Implicit Function Theorem in Banach space to show that the system has a solution for small applied bias. It does not appear that earlier approaches for similar thermistor problems can be employed in this physically important situation. The fact that the problem is cast in a subset of R3 is significant in our presentation.

We prove that every operator preserving orthogonality in a real Banach space is an isometry multiplied by a constant.

Multiple integrals with polyconvex integrands are studied on the class of all sense-preserving diffeomorphisms from W1,p(Ω, Rn) where Ω is an open subset of Rn. They are proved to be sequentially weakly lower semicontinuous if 1 < p = n –1. An example is presented showing that a similar result is not valid if p <n –1.