Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T03:33:06.754Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic behaviour of finite energy solutions of polyharmonic equations

Published online by Cambridge University Press:  14 November 2011

Lao Sen Yu
Lao Sen Yu
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, British Columbia, Canada V6T 1Z2
Get access Rights & Permissions [Opens in a new window]

Synopsis

Asymptotic behaviour of solutions of polyharmonic equations

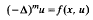
on exterior domains in Rn is considered under suitable conditions on f. It is shown that finite energysolutions u have the asymptotic property

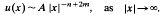
This partially extends results of Egnell [6] for m = 1.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 123 , Issue 2 , 1993 , pp. 345 - 354
Copyright
Copyright © Royal Society of Edinburgh 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Agmon, S.. The Lp approach to the Dirichlet problem. Ann. Scuola Norm. Sup. Pisa 13 (1959), 405–448.Google Scholar
2Allegretto, W. and Yu, L. S.. Decaying solution of 2mth order elliptic problems. Canad. J. Math. 43 (1991), 449–460.CrossRefGoogle Scholar
3Aronszajn, N., Creese, T. M. and Lipkin, L. J.. Polyharmonic Functions (Oxford: Clarendon Press, 1983).Google Scholar
4Dalmasso, R.. Solutions positives globales d'une équation biharmonique sur-linéearie. C.R. Acad. Sci. Paris Ser. 1 Meth 308 (1989), 411–414.Google Scholar
5Edelson, A. L. and Vakilian, R.. Asymptotic behavior of higher order semilinear equations. Nonlinear Anal. 15 (1990), 17–26.Google Scholar
6Egnell, H.. Asymptotic results for finite energy solutions of semilinear elliptic equations (preprint).Google Scholar
7Gilbarg, D. and Trudinger, N. S.. Elliptic Partial Differential Equations of Second Order, 2nd edn (Berlin: Springer, 1983).Google Scholar
8Kusano, T., Naito, M. and Swanson, C. A.. Radial entire solutions of even order semilinear elliptic equations. Canad. J. Math 40 (1988), 1281–1300.CrossRefGoogle Scholar
9Noussair, E. S., Swanson, C. A. and , Yang Jianfu. Transcritical biharmonic equations in Rn. Funkcial Ekvac: (to appear).Google Scholar
10Swanson, C. A. and Yu, L. S.. Radial polyharmonic problems in Rn (preprint).Google Scholar
11Yu, L. S.. Positive Decaying Solutions of Nonlinear Elliptic Problmes (Ph.D. Thesis, University of Alberta, 1990).Google Scholar