Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-14T05:03:58.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Explicit invariant solutions for invariant linear differential operators

Published online by Cambridge University Press:  14 November 2011

Zofia Szmydt  and
Bogdan Ziemian
Zofia Szmydt
Affiliation:
Instytut Matematyczny, Polska Akademia Nauk, Ul Sniadeckich 8, Warszawa, Poland
Bogdan Ziemian
Affiliation:
Instytut Matematyczny, Polska Akademia Nauk, Ul Sniadeckich 8, Warszawa, Poland
Get access Rights & Permissions [Opens in a new window]

Synopsis

Let F be a real analytic function on a real analytic manifold X. Let P be a linear differential operator on X such that 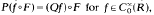, where Q is an ordinary differential operator with analytic coefficients whose singular points are all regular. For each (isolated) critical value z of F, we construct locally an F-invariant solution u of the equation Pu - v, v being an arbitrary F-invariant distribution supported in F−1(z). The solution u is constructed explicitly in the form of a series of F-invariant distributions.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 98 , Issue 1-2 , 1984 , pp. 149 - 166
Copyright
Copyright © Royal Society of Edinburgh 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Cérézo, A.. Equations with constant coefficients invariant under a group of linear transformations. Trans. Amer. Math. Soc. 204 (1975), 267–298.Google Scholar
2Hironaka, H.. Resolution of singularities of an algebraic variety over a field of characteristic zero. Ann. of Math. 79 (1964), 109–326.CrossRefGoogle Scholar
3Jeanquartier, P.. Développement asymptotique de la distribution de Dirac attachée à une fonction analytique. C.R. Acad. Sci. Paris Sér. A 271 (1970), 1159–1161.Google Scholar
4Maire, H. M.. Sur les distributions image reciproque par une fonction analytique. Comment. Math. Helv. 51 (1976), 393–410.CrossRefGoogle Scholar
5Maire, H. M.. Résolution d'opérateurs différentials liés à une fonction analytique. C.R. Acad. Sci. Páris Sér. A 283 (1976), 749–752.Google Scholar
6Methée, P. D.. Sur les distributions invariantes dans le groupe des rotations de Lorentz. Comment. Math. Helv. 28 (1954), 225–269.Google Scholar
7Methée, P. D.. Systemes différentiels du type de Fuchs en théorie des distributions. Comment. Math. Helv. 33 (1959), 38–46.CrossRefGoogle Scholar
8Perron, O.. Über diejenigen Integrale linearer Differentialgleichungen, welche sich an einer Unbestimmtheitsstelle bestimmt verhalten. Math. Ann. 70 (1911), 1–32.CrossRefGoogle Scholar
9Rais, M.. Les solutions invariantes de l'équation des ondes. C.R. Acad. Sci. Paris 259 (1964), 2169–2170.Google Scholar
10de Rham, G.. Solutions élémentaries d'opérateurs différentiels du second ordre. Ann. Inst. Fourier 8 (1958), 337–336.Google Scholar
11Szmydt, Z. and Ziemian, B.. Special solutions of the equations Pu = 0, Pu = δ for invariant linear differential operators with constant coefficients. J. Differential Equations 39 (1981), 226–256.CrossRefGoogle Scholar
12Tengstrand, A.. Distributions invariant under an orthogonal group of arbitrary signature. Math. Scand. 8 (1960), 201–218.Google Scholar
13Ziemian, B.. On G-invariant distributions. J. Differential Equations 35 (1980), 66–86.Google Scholar