The existence of solutions to equations in normed spaces is proved when the nonlinear part of the equation satisfies growth and asymptotic conditions, whether the linear part is invertible or not. For this, we use the coincidence degree theory developed by Mawhin. We apply our abstract results to boundary value problems for nonlinear vector ordinary differential equations. In particular, we consider the Picard boundary value problem at the first eigenvalue and the periodic boundary value problem at resonance. In both cases, the nonlinear term can be of superlinear type. Also, necessary and sufficient conditions of Landesman-Lazer type are obtained.

By using the Halmos-Wallen description of power partial isometries on Hilbert space, we give a complete description of all monogenic inverse semigroups,ℐ. We also describe the full C*-algebra C*ℐ and the reduced C*-algebra C*(ℐ) with particular emphasis on the case of the free monogenic inverse semigroupℑℐt.

Let E be the set of idempotents in Sn, the semigroup of all singular selfmaps of {1,…, n}. For each α in Sn, there is a unique (κ(α)≧1 such that αψEκ,(α). It is known that κ(α)≦ n + cycl α -fix α, where cyclα is the number of cyclic orbits of a and fix α is the number of fixed points. Equality holds only in the case where a is of rank n – 1. An improved upper bound is obtained for κ(α), applying to elements of arbitrary rank. A lower bound is obtained also.

We introduce the notion of a double MS-algebra (L, 0, +) as an MS-algebra (L, 0) whose dual isan MS-algebra (Ld, +), with certain linking conditions concerning the operations x↦x0 and x↦x+. We determine necessary and sufficient conditions whereby an MS-algebra can be made into a double MS-algebra and show that this, when possible, can be done in one and only one way. We also consider the notion of a bistable subvariety of MS-algebras, namely a subvariety R with the property that, for every double MS-algebra (L, 0, +), whenever L, 0 ↦ R, we have (Ld,+)↦ R. Finally, we determine those subvarieties R of MS that are dense (in the sense that every MS-algebra L ↦ R can be made into a double MS-algebra), and those that are sparse (in the sense that if L ↦ R can be made into a double MS-algebra then it belongs to a proper subclass of R).

We deal with the asymptotic behaviour, as t→∞, of complex-valued solutions of nonlinear differential equations

Upper bounds for ∣x(l)(t)∣, 0≦j≦n, are obtained by obtaining upper bounds for solutions u(t) of Bihari-type integral inequalities of the form

This article is concerned with eigenvalue problems of the form Au = λTu in a Hilbert space H, where Ais a selfadjoint positive operator generated by a second-order Sturm-Liouville differential expression and T a selfadjoint indefinite multiplicative operator which is one-to-one. Emphasis is on the full-range and partial-range expansionproperties of the eigenfunctions.

Let P be a set of primes. A nilpotent space X is called “P-universal”, if its P-localization canbe obtained as a direct limit over a sequence of selfmaps of X. A nilpotent fibration is called “fibrewiseP-universal”, if its fibrewise P-localization can be obtained in a similar way as a direct limit of fibrewise maps. In this paper, the following results are proved. Let π:E → B be a nilpotent fibration of connected finite or cofinite spaces. If π is fibrewise P-universal for some proper subset P of the set of primes, then its minimal model (in the sense of D. Sullivan's rational homotopy theory) admits a certaintype of weight decomposition. But the existence of such a weight decomposition implies only that there exists a finite set of primes, such that IT is fibrewise P-universal for all P with . In the absolute case however, i.e.B is a point, the set P can be chosen as the empty set. Thus a result announced by R. Body and D. Sullivan is recovered.

A one-phase Stefan problem can be reduced to an equivalent variational inequality by using the Baiocchi-Duvaut transformation. In this paper, we study the variational inequality by formulating it as a set-valued partial differential equation. The existence of solutions is proved by applying a generalized Schauder fixed fixed point theorem for set-valued mappings. Uniqueness and regularity of solutions are also obtained. In §3, we regard the boundary value Neumann data as boundary controls and combine both the variational inequality and the classical approaches to study the effects of controls on the free boundary and the state (i.e. temperature). In §4, we further use the theory to study an optimal “ice-melting” problem. Our results show that if the controls have fixed total input heat flux and are constrained in magnitude, then the optimal control is “bang-bang”. If the admissible controls are not constrained in magnitude, then the optimal control is a Dirac delta type distribution which is no longer admissible. In the last section, our existence theory is combined with the finite difference method and non-linear programming techniques to obtain numerical solutions.

Let F be a real analytic function on a real analytic manifold X. Let P be a linear differential operator on X such that , where Q is an ordinary differential operator with analytic coefficients whose singular points are all regular. For each (isolated) critical value z of F, we construct locally an F-invariant solution u of the equation Pu - v, v being an arbitrary F-invariant distribution supported in F−1(z). The solution u is constructed explicitly in the form of a series of F-invariant distributions.

Semilinear parabolic equations of the form u1 = ∇2u + δf(u), where f is positive and 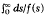is finite, are known to exhibit the phenomenon of blow-up, i.e. for sufficiently large S, u becomes infinite after a finite time t*. We consider one-dimensional problems in the semi-infinite region x>0 and find the time to blow-up (t*). Also, the limiting behaviour of u as t→t*- and x→∞ is determined; in particular, it is seen that u blows up at infinity, i.e. for any given finite x, u is bounded as t→t*. The results are extended to problems with convection.

The modified equation xu, = uxx +f(u) is discussed. This shows the possibility of blow-up at x =0 even if u(0, f) = 0. The manner of blow-up is estimated.

Finally, bounds on the time to blow-up for problems in finite regions are obtained by comparing u with upper and lower solutions.