Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T06:56:39.216Z Has data issue: false hasContentIssue false
  • English
  • Français

Fibrewise P-universal nilpotent fibrations

Published online by Cambridge University Press:  14 November 2011

H. Scheerer
H. Scheerer
Affiliation:
Mathematisches Institut der Freien Universität Berlin, Arnimallee 3, D-1000 Berlin 33, B.R.D.
Get access Rights & Permissions [Opens in a new window]

Synopsis

Let P be a set of primes. A nilpotent space X is called “P-universal”, if its P-localization canbe obtained as a direct limit over a sequence of selfmaps of X. A nilpotent fibration is called “fibrewiseP-universal”, if its fibrewise P-localization can be obtained in a similar way as a direct limit of fibrewise maps. In this paper, the following results are proved. Let π:E → B be a nilpotent fibration of connected finite or cofinite spaces. If π is fibrewise P-universal for some proper subset P of the set of primes, then its minimal model (in the sense of D. Sullivan's rational homotopy theory) admits a certaintype of weight decomposition. But the existence of such a weight decomposition implies only that there exists a finite set 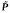of primes, such that IT is fibrewise P-universal for all P with 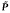. In the absolute case however, i.e.B is a point, the set P can be chosen as the empty set. Thus a result announced by R. Body and D. Sullivan is recovered.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 98 , Issue 1-2 , 1984 , pp. 89 - 104
Copyright
Copyright © Royal Society of Edinburgh 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Berrick, A. J.. The Samelson ex-product. Quart. J. Math. 27 (1976), 173–180.CrossRefGoogle Scholar
2Body, R. and Douglas, R.. Unique factorization of rational homotopy types. Pacific J. Math. 90 (1980), 21–26.CrossRefGoogle Scholar
3Bourbaki, N.. Eléments de mathématique. Groupes et al gébres de Lie, Chap. VII, VIII (Paris: Hermann, 1975).Google Scholar
4Bousfield, A. K. and Kan, D. M.. Homotopy limits, completions and localizations. Lecture Notes in Mathematics 304 (Berlin: Springer, 1972).Google Scholar
5Bousfield, A. K. and Gugenheim, V. K. A. M.. On PL De Rham theory and rational homotopy type. Mem. Amer. Math. Soc. 179 (1976).Google Scholar
6Eggar, M.. The piecing comparison theorem. Indag. Math. 35 (1973), 320–330.CrossRefGoogle Scholar
7Ph. Griffiths, A. and Morgan, J. W.. Rational homotopy theory and differential forms. Progress in Mathematics 16 (Basel: Birkhauser, 1981).Google Scholar
8Halperin, S.. Lectures on minimal models. Publications Internes de l'VU.E.R. de Mathématiques Pures et Appliquées no 111, Université des Sciences et Techniques de Lille.Google Scholar
9Halperin, S. and Thomas, J. C.. Rational equivalence of fibrations with fibre G/K. Canad. J. Math. 34 (1982), 31–43CrossRefGoogle Scholar
10Hilton, P., Mislin, G. and Roitberg, J.. Localization of nilpotent groups and spaces (Amsterdam: North-Holland/American Elsevier, 1975).Google Scholar
11Hilton, P. and Roitberg, J.. On the Zeeman comparison theorem for the homology of quasinilpotent fibrations. Quart. J. Math. 27 (1976), 433–444.CrossRefGoogle Scholar
12Kahn, P. and Scheerer, H.. Localisation des groupes et des espaces nilpotents par des teléscopes. C.R. Acad. Sci. Paris Ser. A 281 (1975), 419–422.Google Scholar
13Kahn, P. and Scheerer, H.. P-universality and fibrewise P-universality in the category of nilpotent groups. Geom. Dedicata 14 (1983), 127–139.CrossRefGoogle Scholar
14Lemaire, C.. P-équivalences de groupes nilpotents. Math. Z. 178 (1981), 163–173.CrossRefGoogle Scholar
15Malcev, A. I.. On a class of homogeneous spaces. Amer. Math. Soc. Transl.(2) 9 (1962), 276–307.Google Scholar
16Mimura, M., Nishida, G. and Toda, H.. Localization of CW-complexes and its applications. J. Math. Soc. Japan 23 (1971),593–624.CrossRefGoogle Scholar
17Mimura, M., O'Neil, R. C. and Toda, H.. On the p-equivalence in the senseof Serre. Japan. J. Math. 40 (1971), 1–10.Google Scholar
18Mimura, M. and Toda, H.. On p-equivalences and p-universal spaces. Comment.- Math. Helv. 46 (1971), 87–97.CrossRefGoogle Scholar
19Quillen, D.. Homotopical Algebra. Lecture Notes in Mathematics 43 (Berlin: Springer, 1967).Google Scholar
20Roitberg, J.. Nilpotent groups, homotopy types, and rational Lie algebras. In Localization in Group Theory and Homotopy Theory. Battelle Seattle Research Center 1974. Ed. by Hilton, P.. Lecture Notes in Mathematics 418, 132–138 (Berlin: Springer, 1974).CrossRefGoogle Scholar
21Roitberg, J.. Rational Lie algebras and P-isomorphisms of nilpotent groups and homotopy types. Comment. Math. Helv. 50 (1975), 1–8. Correction. Comment. Math. Helv. 51 (1976), 435–436.CrossRefGoogle Scholar
22Scheerer, H.. Arithmeticity of groups of fibre homotopy equivalence classes. Manuscripta Math. 31 (1980), 413–424.CrossRefGoogle Scholar
23Serre, J.-P.. Groupes d'homotopie et classes de groupes abéliens. Ann. of Math. 58 (1953), 258–294.CrossRefGoogle Scholar
24Sullivan, D.. Infinitesimal computations in topology. Publications Mathematiques 47 (1977), 269–281 (Paris: Institut des Hautes Etudes Scientifiques).Google Scholar
25Vigue-Poirrier, M.. Réalisation de morphismes donnés en cohomologie et suite spectrale d'Eilenberg-Moore. Trans. Amer. Math. Soc. 265 (1981), 447–484.Google Scholar
26Zabrodsky, A.. Hopf spaces (Amsterdam: North Holland, 1976).Google Scholar