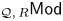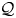Introduction
Model category theory was introduced by Quillen in [Reference Quillen20] to provide a uniform way of formally introducing homotopy theory into general categories, and was heavily applied in various areas such as algebraic topology, category theory and representation theory; see for instance Hovey [Reference Hovey16]. For representation theory, abelian model structures are of significant interest: people try to construct various abelian model structures on abelian categories to obtain the corresponding homotopy theories. The construction of abelian model structures turns out to be equivalent to the construction of Hovey triples by Hovey's correspondence established in [Reference Hovey17]: an abelian model structure on an abelian category $\mathsf {A}$![]() is equivalent to a triple $(\mathsf {C},\, \mathsf {W},\, \mathsf {F})$
is equivalent to a triple $(\mathsf {C},\, \mathsf {W},\, \mathsf {F})$![]() of subcategories of $\mathsf {A}$
of subcategories of $\mathsf {A}$![]() such that $\mathsf {W}$
such that $\mathsf {W}$![]() is thick, and $(\mathsf {C},\, \mathsf {W}\cap \mathsf {F})$
is thick, and $(\mathsf {C},\, \mathsf {W}\cap \mathsf {F})$![]() and $(\mathsf {C}\cap \mathsf {W},\,\mathsf {F})$
and $(\mathsf {C}\cap \mathsf {W},\,\mathsf {F})$![]() are two complete cotorsion pairs, where $\mathsf {W}$
are two complete cotorsion pairs, where $\mathsf {W}$![]() (resp., $\mathsf {C}$
(resp., $\mathsf {C}$![]() and $\mathsf {F}$
and $\mathsf {F}$![]() ) is the subcategory of $\mathsf {A}$
) is the subcategory of $\mathsf {A}$![]() consisting of all trivial (resp., cofibrant and fibrant) objects associated to the corresponding abelian model structure.
consisting of all trivial (resp., cofibrant and fibrant) objects associated to the corresponding abelian model structure.
For an arbitrary associative ring $R$![]() , Šaroch and Št'ovíček described in [Reference Šaroch and Št'ovíček22] three non-trivial abelian model structures on ${_{R}\mathsf {Mod}}$
, Šaroch and Št'ovíček described in [Reference Šaroch and Št'ovíček22] three non-trivial abelian model structures on ${_{R}\mathsf {Mod}}$![]() , the category of left $R$
, the category of left $R$![]() -modules:
-modules:
• a projective model structure $(\mathsf {PGF}(R),\, \mathsf {PGF}(R)^\perp,\, {_{R}\mathsf {Mod}})$
 ,
,• an injective model structure $({_{R}\mathsf {Mod}},\, {^\perp \mathsf {GI}(R)},\, \mathsf {GI}(R))$
 ,
,• and a flat model structure $(\mathsf {GF}(R),\, \mathsf {PGF}(R)^\perp,\, \mathsf {Cot}(R))$
 .
.
Here we recall that an abelian model structure $(\mathsf {C},\, \mathsf {W},\, \mathsf {F})$![]() is called projective (resp., flat) if the subcategory $\mathsf {C}\cap \mathsf {W}$
is called projective (resp., flat) if the subcategory $\mathsf {C}\cap \mathsf {W}$![]() consists of projectives (resp., flats), and it is called injective if the subcategory $\mathsf {W}\cap \mathsf {F}$
consists of projectives (resp., flats), and it is called injective if the subcategory $\mathsf {W}\cap \mathsf {F}$![]() consists of injectives.
consists of injectives.
When one considers the category $\mathsf {Ch}(R)$![]() of chain complexes of left $R$
of chain complexes of left $R$![]() -modules, there are more abelian model structures. In particular, there are
-modules, there are more abelian model structures. In particular, there are
• a projective model structure $(\mathsf {dgPrj}(R),\, \mathsf {Acy},\, \mathsf {Ch}(R))$
 ,
,• an injective model structure $(\mathsf {Ch}(R),\, \mathsf {Acy},\, \mathsf {dgInj}(R))$
 ,
,• and a flat model structure $(\mathsf {dgFlat}(R),\, \mathsf {Acy},\, \mathsf {dgCot}(R))$
 ,
,
and the corresponding homotopy categories of the above three model structures all coincide with $\mathsf {D}(R)$![]() , the derived category of $R$
, the derived category of $R$![]() ; see [Reference Hovey17, exas. 3.2 and 3.3] and Gillespie [Reference Gillespie8, cor. 5.1]. Here $\mathsf {Acy}$
; see [Reference Hovey17, exas. 3.2 and 3.3] and Gillespie [Reference Gillespie8, cor. 5.1]. Here $\mathsf {Acy}$![]() is the subcategory of acyclic complexes, and $\mathsf {dgPrj}(R)$
is the subcategory of acyclic complexes, and $\mathsf {dgPrj}(R)$![]() (resp., $\mathsf {dgInj}(R)$
(resp., $\mathsf {dgInj}(R)$![]() , $\mathsf {dgFlat}(R)$
, $\mathsf {dgFlat}(R)$![]() and $\mathsf {dgCot}(R)$
and $\mathsf {dgCot}(R)$![]() ) is the subcategory of DG-projective (resp., DG-injective, DG-flat and DG-cotorsion) complexes.
) is the subcategory of DG-projective (resp., DG-injective, DG-flat and DG-cotorsion) complexes.
Since $\mathsf {Ch}(R)$![]() can be viewed as a functor category in a natural way (see [Reference Holm and Jørgensen14, exa. 8.13]), one may wonder to extend the above model structures to functor categories. This was considered by Holm and Jørgensen recently in [Reference Holm and Jørgensen14], where they constructed the projective and injective model structures on the category ${_{\mathcal {Q},\,R}\mathsf {Mod}}$
can be viewed as a functor category in a natural way (see [Reference Holm and Jørgensen14, exa. 8.13]), one may wonder to extend the above model structures to functor categories. This was considered by Holm and Jørgensen recently in [Reference Holm and Jørgensen14], where they constructed the projective and injective model structures on the category ${_{\mathcal {Q},\,R}\mathsf {Mod}}$![]() of additive functors from a small preadditive category $\mathcal {Q}$
of additive functors from a small preadditive category $\mathcal {Q}$![]() satisfying certain conditions specified in [Reference Holm and Jørgensen14, Setup 2.5] (see also Setup 2.6) to the category ${_{R}\mathsf {Mod}}$
satisfying certain conditions specified in [Reference Holm and Jørgensen14, Setup 2.5] (see also Setup 2.6) to the category ${_{R}\mathsf {Mod}}$![]() for any associative ring $R$
for any associative ring $R$![]() . Explicitly, they proved in [Reference Holm and Jørgensen14, thm. A] that there are
. Explicitly, they proved in [Reference Holm and Jørgensen14, thm. A] that there are
• a projective model structure $({^\perp \mathsf {E}},\, \mathsf {E},\, {_{\mathcal {Q},\,R}\mathsf {Mod}})$
 ,
,• and an injective model structure $({_{\mathcal {Q},\,R}\mathsf {Mod}},\, \mathsf {E},\, \mathsf {E}^\perp )$

on ${_{\mathcal {Q},\,R}\mathsf {Mod}}$![]() , where $\mathsf {E} = \{X \in {_{\mathcal {Q},\,R}\mathsf {Mod}}\ | X^{\natural }\ \mathrm {has\ finite\ projective\ dimension in}\ {_{\mathcal {Q}}\mathsf {Mod}}\}$
, where $\mathsf {E} = \{X \in {_{\mathcal {Q},\,R}\mathsf {Mod}}\ | X^{\natural }\ \mathrm {has\ finite\ projective\ dimension in}\ {_{\mathcal {Q}}\mathsf {Mod}}\}$![]() . Here $(-)^{\natural }$
. Here $(-)^{\natural }$![]() denotes the forgetful functor from ${_{\mathcal {Q},\,R}\mathsf {Mod}}$
denotes the forgetful functor from ${_{\mathcal {Q},\,R}\mathsf {Mod}}$![]() to ${_{\mathcal {Q}}\mathsf {Mod}}$
to ${_{\mathcal {Q}}\mathsf {Mod}}$![]() . Both model structures have the same homotopy category called the $\mathcal {Q}$
. Both model structures have the same homotopy category called the $\mathcal {Q}$![]() -shaped derived category. In particular, by taking $\mathcal {Q}$
-shaped derived category. In particular, by taking $\mathcal {Q}$![]() to be a special category, their result includes the projective and injective model structures on $\mathsf {Ch}(R)$
to be a special category, their result includes the projective and injective model structures on $\mathsf {Ch}(R)$![]() as examples.
as examples.
We note that the flat model structure on $\mathsf {Ch}(R)$![]() was not extended to the more general framework in [Reference Holm and Jørgensen14]. As the first main result of this paper, we fill this gap by describing a flat model structure on ${_{\mathcal {Q},\,R}\mathsf {Mod}}$
was not extended to the more general framework in [Reference Holm and Jørgensen14]. As the first main result of this paper, we fill this gap by describing a flat model structure on ${_{\mathcal {Q},\,R}\mathsf {Mod}}$![]() whose homotopy category also coincides with the $\mathcal {Q}$
whose homotopy category also coincides with the $\mathcal {Q}$![]() -shaped derived category. The following is a special case of corollary 2.8 with $\mathbb {k}=\mathbb {Z}$
-shaped derived category. The following is a special case of corollary 2.8 with $\mathbb {k}=\mathbb {Z}$![]() .
.
Theorem A Let $\mathcal {Q}$![]() be a small preadditive category satisfying the conditions specified in setup 2.6. Then for any associative ring $R$
be a small preadditive category satisfying the conditions specified in setup 2.6. Then for any associative ring $R$![]() , there is a hereditary abelian model structure
, there is a hereditary abelian model structure
on ${_{\mathcal {Q},\,R}\mathsf {Mod}}$![]() , where $^{\perp }(\mathsf {Cot}(\mathcal {Q},\,R)\cap \mathsf {E})$
, where $^{\perp }(\mathsf {Cot}(\mathcal {Q},\,R)\cap \mathsf {E})$![]() is the subcategory of cofibrant objects, $\mathsf {E}$
is the subcategory of cofibrant objects, $\mathsf {E}$![]() is the subcategory of trivial objects and $\mathsf {Cot}(\mathcal {Q},\,R)$
is the subcategory of trivial objects and $\mathsf {Cot}(\mathcal {Q},\,R)$![]() is the subcategory of fibrant objects.
is the subcategory of fibrant objects.
Members in $\mathsf {Cot}(\mathcal {Q},\,R)$![]() are cotorsion objects in ${_{\mathcal {Q},\,R}\mathsf {Mod}}$
are cotorsion objects in ${_{\mathcal {Q},\,R}\mathsf {Mod}}$![]() defined in 1.5.
defined in 1.5.
We mention that the key ingredient to prove theorem A is a recent result on Gorenstein homological objects by Šaroch and Št'ovíček [Reference Šaroch and Št'ovíček22]; see lemma 2.1. For a Gorenstein ring $R$![]() and a small preadditive category $\mathcal {Q}$
and a small preadditive category $\mathcal {Q}$![]() satisfying conditions (1)–(3) in setup 2.6, it is known that an object $X$
satisfying conditions (1)–(3) in setup 2.6, it is known that an object $X$![]() in ${_{\mathcal {Q},\, R}\mathsf {Mod}}$
in ${_{\mathcal {Q},\, R}\mathsf {Mod}}$![]() is Gorenstein projective if and only if each left $R$
is Gorenstein projective if and only if each left $R$![]() -module $X(q)$
-module $X(q)$![]() is Gorenstein projective for $q\in \mathcal {Q}$
is Gorenstein projective for $q\in \mathcal {Q}$![]() ; see Dell'Ambrogio, Stevenson and Šťovíček [Reference Dell'Ambrogio, Stevenson and Šťovíček4, cor. 4.8]. Note that chain complexes of left $R$
; see Dell'Ambrogio, Stevenson and Šťovíček [Reference Dell'Ambrogio, Stevenson and Šťovíček4, cor. 4.8]. Note that chain complexes of left $R$![]() -modules can be regarded as additive functors from a special small preadditive category to the category ${_{R}\mathsf {Mod}}$
-modules can be regarded as additive functors from a special small preadditive category to the category ${_{R}\mathsf {Mod}}$![]() of left $R$
of left $R$![]() -modules. The result [Reference Dell'Ambrogio, Stevenson and Šťovíček4, cor. 4.8] is a generalization of [Reference Enochs and García Rozas6, thm. 4.5] by Enochs and García Rozas: an unbounded chain complex $M$
-modules. The result [Reference Dell'Ambrogio, Stevenson and Šťovíček4, cor. 4.8] is a generalization of [Reference Enochs and García Rozas6, thm. 4.5] by Enochs and García Rozas: an unbounded chain complex $M$![]() of left $R$
of left $R$![]() -modules is Gorenstein projective if and only if each left $R$
-modules is Gorenstein projective if and only if each left $R$![]() -module $M_i$
-module $M_i$![]() is Gorenstein projective for $i \in \mathbb {Z}$
is Gorenstein projective for $i \in \mathbb {Z}$![]() under the extra assumption that $R$
under the extra assumption that $R$![]() is a Gorenstein ring. Since in [Reference Liu and Zhang18, Reference Yang and Liu23] Liu, Yang and Zhang have shown that [Reference Enochs and García Rozas6, thm. 4.5] actually holds for arbitrary associative rings, it is then natural to ask if [Reference Dell'Ambrogio, Stevenson and Šťovíček4, cor. 4.8] also holds for these small preadditive categories $\mathcal {Q}$
is a Gorenstein ring. Since in [Reference Liu and Zhang18, Reference Yang and Liu23] Liu, Yang and Zhang have shown that [Reference Enochs and García Rozas6, thm. 4.5] actually holds for arbitrary associative rings, it is then natural to ask if [Reference Dell'Ambrogio, Stevenson and Šťovíček4, cor. 4.8] also holds for these small preadditive categories $\mathcal {Q}$![]() without any restriction on the coefficient ring $R$
without any restriction on the coefficient ring $R$![]() .
.
Our second main result answers this question affirmatively. Relying on the concept of Frobenius functors introduced by Chen and Ren in [Reference Chen and Ren2] and a main result of that paper, we prove that an additive functor $X$![]() from $\mathcal {Q}$
from $\mathcal {Q}$![]() to ${_{R}\mathsf {Mod}}$
to ${_{R}\mathsf {Mod}}$![]() is Gorenstein projective (resp., Gorenstein injective, Gorenstein flat, projective coresolving Gorenstein flat) if and only if so is each left $R$
is Gorenstein projective (resp., Gorenstein injective, Gorenstein flat, projective coresolving Gorenstein flat) if and only if so is each left $R$![]() -module $X(q)$
-module $X(q)$![]() in the following result, which is a special case of theorems 3.6, 3.7, 3.11 and 3.12 with $\mathbb {k}=\mathbb {Z}$
in the following result, which is a special case of theorems 3.6, 3.7, 3.11 and 3.12 with $\mathbb {k}=\mathbb {Z}$![]() .
.
Theorem B Let $\mathcal {Q}$![]() be a small preadditive category satisfying conditions (1)–(3) in setup 2.6 and $R$
be a small preadditive category satisfying conditions (1)–(3) in setup 2.6 and $R$![]() an arbitrary associative ring. Then an object $X\in {_{\mathcal {Q},\,R}\mathsf {Mod}}$
an arbitrary associative ring. Then an object $X\in {_{\mathcal {Q},\,R}\mathsf {Mod}}$![]() is Gorenstein projecitve (resp., Gorenstein injective, Gorenstein flat, projectively coresolved Gorenstein flat) if and only if each left $R$
is Gorenstein projecitve (resp., Gorenstein injective, Gorenstein flat, projectively coresolved Gorenstein flat) if and only if each left $R$![]() -module $X(q)$
-module $X(q)$![]() is Gorenstein projecitve (resp., Gorenstein injective, Gorenstein flat, projectively coresolved Gorenstein flat) for $q\in \mathcal {Q}$
is Gorenstein projecitve (resp., Gorenstein injective, Gorenstein flat, projectively coresolved Gorenstein flat) for $q\in \mathcal {Q}$![]() .
.
1. Preliminaries
Throughout this paper, by the term ‘subcategory’ we always mean a full subcategory which is closed under isomorphisms and contains the zero object. We assume that $\mathbb {k}$![]() is a commutative ring and $A$
is a commutative ring and $A$![]() is an associative $\mathbb {k}$
is an associative $\mathbb {k}$![]() -algebra, and assume that $\mathcal {C}$
-algebra, and assume that $\mathcal {C}$![]() is a small $\mathbb {k}$
is a small $\mathbb {k}$![]() -linear category such that $\mathcal {C}(p,\,q)$
-linear category such that $\mathcal {C}(p,\,q)$![]() is a projective $\mathbb {k}$
is a projective $\mathbb {k}$![]() -module for each pair of objects $p$
-module for each pair of objects $p$![]() and $q$
and $q$![]() in $\mathcal {C}$
in $\mathcal {C}$![]() .
.
Let ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() be the category of $\mathbb {k}$
be the category of $\mathbb {k}$![]() -linear functors from $\mathcal {C}$
-linear functors from $\mathcal {C}$![]() to the left $A$
to the left $A$![]() -module category ${_{A}\mathsf {Mod}}$
-module category ${_{A}\mathsf {Mod}}$![]() , and let $\mathsf {Mod}_{\mathcal {C},\,A}$
, and let $\mathsf {Mod}_{\mathcal {C},\,A}$![]() be the category of $\mathbb {k}$
be the category of $\mathbb {k}$![]() -linear functors from $\mathcal {C}^{\sf op}$
-linear functors from $\mathcal {C}^{\sf op}$![]() to the right $A$
to the right $A$![]() -module category $\mathsf {Mod}_{A}$
-module category $\mathsf {Mod}_{A}$![]() . In this section, we collect some basic results on homological objects in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
. In this section, we collect some basic results on homological objects in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() , which will be used frequently in the paper.
, which will be used frequently in the paper.
1.1 (Cotorsion pairs)
Let $\mathsf {A}$![]() be an abelian category with enough projectives and injectives. A pair $(\mathsf {C},\, \mathsf {W})$
be an abelian category with enough projectives and injectives. A pair $(\mathsf {C},\, \mathsf {W})$![]() of subcategories of $\mathsf {A}$
of subcategories of $\mathsf {A}$![]() is called a cotorsion pair if $\mathsf {C}^{\bot }=\mathsf {W}$
is called a cotorsion pair if $\mathsf {C}^{\bot }=\mathsf {W}$![]() and $^{\bot }\mathsf {W}=\mathsf {C}$
and $^{\bot }\mathsf {W}=\mathsf {C}$![]() . Here
. Here

It is clear that $({^\perp (\mathsf {C}^\perp )},\,\mathsf {C}^\perp )$![]() is a cotorsion pair, which is called a cotorsion pair generated by $\mathsf {C}$
is a cotorsion pair, which is called a cotorsion pair generated by $\mathsf {C}$![]() . Recall from e.g. Enochs and Jenda [Reference Enochs and Jenda7] that a cotorsion pair $(\mathsf {C},\,\mathsf {W})$
. Recall from e.g. Enochs and Jenda [Reference Enochs and Jenda7] that a cotorsion pair $(\mathsf {C},\,\mathsf {W})$![]() is complete if for each object $M$
is complete if for each object $M$![]() in $\mathsf {A}$
in $\mathsf {A}$![]() there is an exact sequence $0 \to M \to W \to C \to 0$
there is an exact sequence $0 \to M \to W \to C \to 0$![]() with $W\in \mathsf {W}$
with $W\in \mathsf {W}$![]() and $C\in \mathsf {C}$
and $C\in \mathsf {C}$![]() (or there is an exact sequence $0 \to W' \to C' \to M \to 0$
(or there is an exact sequence $0 \to W' \to C' \to M \to 0$![]() with $W'\in \mathsf {W}$
with $W'\in \mathsf {W}$![]() and $C'\in \mathsf {C}$
and $C'\in \mathsf {C}$![]() ). A cotorsion pair $(\mathsf {C},\,\mathsf {W})$
). A cotorsion pair $(\mathsf {C},\,\mathsf {W})$![]() is called hereditary if $\mathsf {C}$
is called hereditary if $\mathsf {C}$![]() is closed under kernels of epimorphisms or $\mathsf {W}$
is closed under kernels of epimorphisms or $\mathsf {W}$![]() is closed under cokernels of monomorphisms.
is closed under cokernels of monomorphisms.
The following notion of projective/injective cotorsion pairs can be found in Gillespie [Reference Gillespie10, def. 3.4].
Definition 1.2 Let $\mathsf {A}$![]() be an abelian category with enough projectives and injectives. A complete cotorsion pair $(\mathsf {C},\, \mathsf {W})$
be an abelian category with enough projectives and injectives. A complete cotorsion pair $(\mathsf {C},\, \mathsf {W})$![]() is said to be projective if $\mathsf {W}$
is said to be projective if $\mathsf {W}$![]() is thick (i.e. if two out of three of the terms in a short exact sequence are in $\mathsf {W}$
is thick (i.e. if two out of three of the terms in a short exact sequence are in $\mathsf {W}$![]() , then so is the third) and $\mathsf {C}\cap \mathsf {W}$
, then so is the third) and $\mathsf {C}\cap \mathsf {W}$![]() coincides with the subcategory of projective objects. The notion of injective cotorsion pairs is defined dually.
coincides with the subcategory of projective objects. The notion of injective cotorsion pairs is defined dually.
Remark 1.3 A projective cotorsion pair $(\mathsf {C},\, \mathsf {W})$![]() determines a projective model structure on $\mathsf {A}$
determines a projective model structure on $\mathsf {A}$![]() such that $\mathsf {C}$
such that $\mathsf {C}$![]() is the subcategory of cofibrant objects, $\mathsf {W}$
is the subcategory of cofibrant objects, $\mathsf {W}$![]() is the subcategory of trivial objects and all objects in $\mathsf {A}$
is the subcategory of trivial objects and all objects in $\mathsf {A}$![]() are fibrant objects. Dually, an injective cotorsion pair $(\mathsf {W},\, \mathsf {F})$
are fibrant objects. Dually, an injective cotorsion pair $(\mathsf {W},\, \mathsf {F})$![]() determines an injective model structure on $\mathsf {A}$
determines an injective model structure on $\mathsf {A}$![]() such that $\mathsf {F}$
such that $\mathsf {F}$![]() is the subcategory of fibrant objects, $\mathsf {W}$
is the subcategory of fibrant objects, $\mathsf {W}$![]() is the subcategory of trivial objects and all objects in $\mathsf {A}$
is the subcategory of trivial objects and all objects in $\mathsf {A}$![]() are cofibrant objects.
are cofibrant objects.
1.4 (Flat objects)
Let $\mathsf {G}$![]() be a locally finitely presentable (in the sense of Crawley–Boevey [Reference Crawley-Boevey3, §1]) Grothendieck category admitting enough projectives. A sequence
be a locally finitely presentable (in the sense of Crawley–Boevey [Reference Crawley-Boevey3, §1]) Grothendieck category admitting enough projectives. A sequence
in $\mathsf {G}$![]() is said to be pure if for each finitely presentable object $T$
is said to be pure if for each finitely presentable object $T$![]() , the sequence
, the sequence
is exact (in this case, $M\to N\to 0$![]() is called a pure epimorphism). An object $F$
is called a pure epimorphism). An object $F$![]() in $\mathsf {G}$
in $\mathsf {G}$![]() is called flat if every epimorphism $M\to F$
is called flat if every epimorphism $M\to F$![]() is a pure epimorphism. It is not difficult to check that $F$
is a pure epimorphism. It is not difficult to check that $F$![]() is flat if and only if it is a filtered colimit of finitely generated projective objects. Let ${\sf Flat(\mathsf {G})}$
is flat if and only if it is a filtered colimit of finitely generated projective objects. Let ${\sf Flat(\mathsf {G})}$![]() be the subcategory of flat objects in $\mathsf {G}$
be the subcategory of flat objects in $\mathsf {G}$![]() . Then ${\sf Flat(\mathsf {G})}$
. Then ${\sf Flat(\mathsf {G})}$![]() is closed under extensions, filtered colimits and pure epimorphisms by Rump [Reference Rump21, prop. 7], and so the pair $({\sf Flat(\mathsf {G})},\, {\sf Flat(\mathsf {G})}^\perp )$
is closed under extensions, filtered colimits and pure epimorphisms by Rump [Reference Rump21, prop. 7], and so the pair $({\sf Flat(\mathsf {G})},\, {\sf Flat(\mathsf {G})}^\perp )$![]() is a complete and hereditary cotorsion pair generated by a set by the proof of [Reference Holm and Jørgensen14, prop. A.3], that is, there is a set $\mathsf {S}\subseteq {\sf Flat(\mathsf {G})}$
is a complete and hereditary cotorsion pair generated by a set by the proof of [Reference Holm and Jørgensen14, prop. A.3], that is, there is a set $\mathsf {S}\subseteq {\sf Flat(\mathsf {G})}$![]() such that $\mathsf {S}^\perp = {\sf Flat(\mathsf {G})}^\perp$
such that $\mathsf {S}^\perp = {\sf Flat(\mathsf {G})}^\perp$![]() .
.
1.5 It follows from [Reference Holm and Jørgensen14, prop. 3.12] that ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() is a locally finitely presentable Grothendieck category admitting enough projectives. Let $\mathsf {Flat}(\mathcal {C},\,A)$
is a locally finitely presentable Grothendieck category admitting enough projectives. Let $\mathsf {Flat}(\mathcal {C},\,A)$![]() be the subcategory of flat objects in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
be the subcategory of flat objects in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() . An object $X$
. An object $X$![]() in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() is called cotorsion if it is in $\mathsf {Flat}(\mathcal {C},\,A)^\perp$
is called cotorsion if it is in $\mathsf {Flat}(\mathcal {C},\,A)^\perp$![]() . Denote the subcategory of cotorsion objects by $\mathsf {Cot}(\mathcal {C},\,A)$
. Denote the subcategory of cotorsion objects by $\mathsf {Cot}(\mathcal {C},\,A)$![]() . Then by 1.4, the pair $(\mathsf {Flat}(\mathcal {C},\,A),\, \mathsf {Cot}(\mathcal {C},\,A))$
. Then by 1.4, the pair $(\mathsf {Flat}(\mathcal {C},\,A),\, \mathsf {Cot}(\mathcal {C},\,A))$![]() is a complete and hereditary cotorsion pair generated by a set.
is a complete and hereditary cotorsion pair generated by a set.
1.6 (Tensor products in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() )
)
Following Oberst and Röhrl [Reference Oberst and Röhrl19], we define a tensor product functor $-\otimes _{\mathcal {C},A}-: \mathsf {Mod}_{\mathcal {C},\,A}\times {_{\mathcal {C},\,A}\mathsf {Mod}}\to {_{\mathbb {k}}\mathsf {Mod}}$![]() ; it is right exact in each variable.
; it is right exact in each variable.
Let $X\in {_{\mathcal {C},\,A}\mathsf {Mod}}$![]() . We construct for any $\mathbb {k}$
. We construct for any $\mathbb {k}$![]() -module $G$
-module $G$![]() , an object $\operatorname {Hom}_{\mathbb {k}}\left (X,G\right )\in \mathsf {Mod}_{\mathcal {C},\,A}$
, an object $\operatorname {Hom}_{\mathbb {k}}\left (X,G\right )\in \mathsf {Mod}_{\mathcal {C},\,A}$![]() as follows:
as follows:
• For each $q\in \mathcal {C}^{\sf op}$
 let $\operatorname {Hom}_{\mathbb {k}}\left (X,G\right )(q)=\operatorname {Hom}_{\mathbb {k}}\left (X(q),G\right )\in \mathsf {Mod}_{A}$
let $\operatorname {Hom}_{\mathbb {k}}\left (X,G\right )(q)=\operatorname {Hom}_{\mathbb {k}}\left (X(q),G\right )\in \mathsf {Mod}_{A}$ .
.• For each morphism $f: p\to q$
 in $\mathcal {C}^{\sf op}$
in $\mathcal {C}^{\sf op}$ let $\operatorname {Hom}_{\mathbb {k}}\left (X,G\right )(f)=\operatorname {Hom}_{\mathbb {k}}\left (X(f^{\sf op}),G\right ):\operatorname {Hom}_{\mathbb {k}}\left (X(p),G\right )\to \operatorname {Hom}_{\mathbb {k}}\left (X(q),G\right )$
let $\operatorname {Hom}_{\mathbb {k}}\left (X,G\right )(f)=\operatorname {Hom}_{\mathbb {k}}\left (X(f^{\sf op}),G\right ):\operatorname {Hom}_{\mathbb {k}}\left (X(p),G\right )\to \operatorname {Hom}_{\mathbb {k}}\left (X(q),G\right )$ .
.
It is evident that $\operatorname {Hom}_{\mathbb {k}}\left (X,-\right )$![]() is a functor from the category ${_{\mathbb {k}}\mathsf {Mod}}$
is a functor from the category ${_{\mathbb {k}}\mathsf {Mod}}$![]() to $\mathsf {Mod}_{\mathcal {C},\,A}$
to $\mathsf {Mod}_{\mathcal {C},\,A}$![]() . This functor is left exact and preserves arbitrary products, so it has a left adjoint functor from $\mathsf {Mod}_{\mathcal {C},\,A}$
. This functor is left exact and preserves arbitrary products, so it has a left adjoint functor from $\mathsf {Mod}_{\mathcal {C},\,A}$![]() to ${_{\mathbb {k}}\mathsf {Mod}}$
to ${_{\mathbb {k}}\mathsf {Mod}}$![]() , which is denoted $-\otimes _{\mathcal {C},A} X$
, which is denoted $-\otimes _{\mathcal {C},A} X$![]() and will play the role of the tensor product in our work. Then for each $Y\in \mathsf {Mod}_{\mathcal {C},\,A}$
and will play the role of the tensor product in our work. Then for each $Y\in \mathsf {Mod}_{\mathcal {C},\,A}$![]() there are natural isomorphisms
there are natural isomorphisms
Notation 1.7 Let $\mathsf {Prj}(\mathcal {C},\,A)$![]() (resp., $\mathsf {Inj}(\mathcal {C},\,A)$
(resp., $\mathsf {Inj}(\mathcal {C},\,A)$![]() ) be the subcategory of projective objects (resp., injective objects) in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
) be the subcategory of projective objects (resp., injective objects) in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() . In the case that $A=\mathbb {k}$
. In the case that $A=\mathbb {k}$![]() , we write ${_{\mathcal {C}}\mathsf {Mod}}$
, we write ${_{\mathcal {C}}\mathsf {Mod}}$![]() (resp., $\mathsf {Prj}(\mathcal {C})$
(resp., $\mathsf {Prj}(\mathcal {C})$![]() , $\mathsf {Inj}(\mathcal {C})$
, $\mathsf {Inj}(\mathcal {C})$![]() , $\mathsf {Flat}(\mathcal {C})$
, $\mathsf {Flat}(\mathcal {C})$![]() and $\mathsf {Cot}(\mathcal {C})$
and $\mathsf {Cot}(\mathcal {C})$![]() ) instead of ${_{\mathcal {C},\,\mathbb {k}}\mathsf {Mod}}$
) instead of ${_{\mathcal {C},\,\mathbb {k}}\mathsf {Mod}}$![]() (resp., $\mathsf {Prj}(\mathcal {C},\,\mathbb {k})$
(resp., $\mathsf {Prj}(\mathcal {C},\,\mathbb {k})$![]() , $\mathsf {Inj}(\mathcal {C},\,\mathbb {k})$
, $\mathsf {Inj}(\mathcal {C},\,\mathbb {k})$![]() , $\mathsf {Flat}(\mathcal {C},\,\mathbb {k})$
, $\mathsf {Flat}(\mathcal {C},\,\mathbb {k})$![]() and $\mathsf {Cot}(\mathcal {C},\,\mathbb {k})$
and $\mathsf {Cot}(\mathcal {C},\,\mathbb {k})$![]() ), and we write $-\otimes _{\mathcal {C}}-$
), and we write $-\otimes _{\mathcal {C}}-$![]() instead of $-\otimes _{\mathcal {C},\mathbb {k}}-$
instead of $-\otimes _{\mathcal {C},\mathbb {k}}-$![]() .
.
1.8 By [Reference Holm and Jørgensen14, Corollary 3.9], for every object $q$![]() in $\mathcal {C}$
in $\mathcal {C}$![]() there is an adjoint triple $(F_{q},\,E_{q},\,G_{q})$
there is an adjoint triple $(F_{q},\,E_{q},\,G_{q})$![]() as follows:
as follows:

It is clear that the evaluation functor $E_q$![]() is exact. Since $\mathcal {C}(p,\,q)$
is exact. Since $\mathcal {C}(p,\,q)$![]() is a projective $\mathbb {k}$
is a projective $\mathbb {k}$![]() -module for each pair of objects $p$
-module for each pair of objects $p$![]() and $q$
and $q$![]() in $\mathcal {C}$
in $\mathcal {C}$![]() by the assumption, both the functors $F_q$
by the assumption, both the functors $F_q$![]() and $G_q$
and $G_q$![]() are exact as well. Then by Holm and Jørgensen [Reference Holm and Jørgensen12, lem. 5.1], we have the following result.
are exact as well. Then by Holm and Jørgensen [Reference Holm and Jørgensen12, lem. 5.1], we have the following result.
Lemma 1.9 Let $X$![]() be an object in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
be an object in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() and $q$
and $q$![]() an object in $\mathcal {C}$
an object in $\mathcal {C}$![]() . Then for each $M \in {_{A}\mathsf {Mod}}$
. Then for each $M \in {_{A}\mathsf {Mod}}$![]() and $n \geqslant 0$
and $n \geqslant 0$![]() , there are isomorphisms
, there are isomorphisms
and
The following proposition asserts that the evaluation functor preserves special homological property: if an object (which is a functor) in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() has a certain special homological property, so does its value on each object in $\mathcal {C}$
has a certain special homological property, so does its value on each object in $\mathcal {C}$![]() .
.
Proposition 1.10 Let $X$![]() be an object in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
be an object in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() and $q$
and $q$![]() an object in $\mathcal {C}$
an object in $\mathcal {C}$![]() . Then the following statements hold.
. Then the following statements hold.
(a) If $X\in \mathsf {Prj}(\mathcal {C},\,A)$
 , then $X(q)\in \mathsf {Prj}(A)$
, then $X(q)\in \mathsf {Prj}(A)$ .
.(b) If $X\in \mathsf {Inj}(\mathcal {C},\,A)$
 , then $X(q)\in \mathsf {Inj}(A)$
, then $X(q)\in \mathsf {Inj}(A)$ .
.(c) If $X\in \mathsf {Flat}(\mathcal {C},\,A)$
 , then $X(q)\in \mathsf {Flat}(A)$
, then $X(q)\in \mathsf {Flat}(A)$ .
.(d) If $X\in \mathsf {Cot}(\mathcal {C},\,A)$
 , then $X(q)\in \mathsf {Cot}(A)$
, then $X(q)\in \mathsf {Cot}(A)$ .
.
Proof. Statements (a) and (b) hold since the functors $F_q$![]() and $G_q$
and $G_q$![]() are exact. For $X \in \mathsf {Flat}(\mathcal {C},\,A)$
are exact. For $X \in \mathsf {Flat}(\mathcal {C},\,A)$![]() , one has $X \cong {\rm colim}_iP_i$
, one has $X \cong {\rm colim}_iP_i$![]() with $P_i \in \mathsf {Prj}(\mathcal {C},\,A)$
with $P_i \in \mathsf {Prj}(\mathcal {C},\,A)$![]() , and deduce by (a) that
, and deduce by (a) that
so the statement (c) is true.
To verify the statement (d), we fix a flat left $A$![]() -module $M$
-module $M$![]() and write $M = {\rm colim}_i T_i$
and write $M = {\rm colim}_i T_i$![]() with each $T_i$
with each $T_i$![]() a projective left $A$
a projective left $A$![]() -module. It follows that each $F_q(T_i)$
-module. It follows that each $F_q(T_i)$![]() is projective and $F_q(M)\cong {\rm colim}_iF_q(T_i)$
is projective and $F_q(M)\cong {\rm colim}_iF_q(T_i)$![]() is flat in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
is flat in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() . By lemma 1.9, one has
. By lemma 1.9, one has
Therefore, $X(q)$![]() is a cotorsion left $A$
is a cotorsion left $A$![]() -module.
-module.
Corollary 1.11 Let $N$![]() be a cotorsion left $A$
be a cotorsion left $A$![]() -module and $q$
-module and $q$![]() an object in $\mathcal {C}$
an object in $\mathcal {C}$![]() . Then $G_{q}(N)$
. Then $G_{q}(N)$![]() is a cotorsion object in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
is a cotorsion object in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() .
.
Proof. Take an arbitrary flat object $X$![]() in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() . Then by lemma 1.9
. Then by lemma 1.9
as $X(q)$![]() is flat by proposition 1.10(c).
is flat by proposition 1.10(c).
1.12 Let $(-)^{\natural }$![]() denote the forgetful functor from ${_{\mathcal {C},\,A}\mathsf {Mod}}$
denote the forgetful functor from ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() to ${_{\mathcal {C}}\mathsf {Mod}}$
to ${_{\mathcal {C}}\mathsf {Mod}}$![]() . Then $(-)^{\natural }$
. Then $(-)^{\natural }$![]() is an exact functor and there is an adjoint triple as follows (see [Reference Holm and Jørgensen14, cor. 3.5]):
is an exact functor and there is an adjoint triple as follows (see [Reference Holm and Jørgensen14, cor. 3.5]):

Proposition 1.13 Let $X$![]() be an object in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
be an object in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() . Then the following statements hold.
. Then the following statements hold.
(a) If $X \in \mathsf {Prj}(\mathcal {C},\,A)$
 , then the projective dimension of $X^\natural$
, then the projective dimension of $X^\natural$ is bounded by ${\rm pd}_\mathbb {k} A$
is bounded by ${\rm pd}_\mathbb {k} A$ .
.(b) If $X \in \mathsf {Inj}(\mathcal {C},\,A)$
 , then the injective dimension $X^\natural$
, then the injective dimension $X^\natural$ is bounded by ${\rm fd}_\mathbb {k} A$
is bounded by ${\rm fd}_\mathbb {k} A$ .
.(c) If $X \in \mathsf {Flat}(\mathcal {C},\,A)$
 , then the flat dimension of $X^\natural$
, then the flat dimension of $X^\natural$ is bounded by ${\rm pd}_\mathbb {k} A$
is bounded by ${\rm pd}_\mathbb {k} A$ .
.
Proof. In the following, we use the symbols ${\rm pd}_\mathcal {C}(-)$![]() , $\mathrm {id}_\mathcal {C}(-)$
, $\mathrm {id}_\mathcal {C}(-)$![]() and ${\rm fd}_\mathcal {C}(-)$
and ${\rm fd}_\mathcal {C}(-)$![]() to denote the projective, injective and flat dimension of objects in ${_{\mathcal {C}}\mathsf {Mod}}$
to denote the projective, injective and flat dimension of objects in ${_{\mathcal {C}}\mathsf {Mod}}$![]() , respectively.
, respectively.
(a). For each object $q$![]() in $\mathcal {C}$
in $\mathcal {C}$![]() , one has $F_q(A)^\natural = \mathcal {C}(q,\,-) \otimes _\mathbb {k} A^\natural$
, one has $F_q(A)^\natural = \mathcal {C}(q,\,-) \otimes _\mathbb {k} A^\natural$![]() . Since the functor
. Since the functor
preserves projective objects and is exact, we deduce that
Thus by [Reference Holm and Jørgensen14, prop. 3.12(a)], one has ${\rm pd}_\mathcal {C} X^\natural \leqslant {\rm pd}_\mathbb {k} A$![]() .
.
(b). For each object $q$![]() in $\mathcal {C}$
in $\mathcal {C}$![]() and $I \in \mathsf {Inj}(A)$
and $I \in \mathsf {Inj}(A)$![]() , one has $G_q(I)^\natural = \operatorname {Hom}_{\mathbb {k}}\left (\mathcal {C}(-,\,q),I^\natural \right )$
, one has $G_q(I)^\natural = \operatorname {Hom}_{\mathbb {k}}\left (\mathcal {C}(-,\,q),I^\natural \right )$![]() . Since the functor $\operatorname {Hom}_{\mathbb {k}}\left (\mathcal {C}(-,\,q),-\right ): {_{\mathbb {k}}\mathsf {Mod}}\to {_{\mathcal {C}}\mathsf {Mod}}$
. Since the functor $\operatorname {Hom}_{\mathbb {k}}\left (\mathcal {C}(-,\,q),-\right ): {_{\mathbb {k}}\mathsf {Mod}}\to {_{\mathcal {C}}\mathsf {Mod}}$![]() preserves injective objects and is exact, one has
preserves injective objects and is exact, one has
where the last inequality holds by Avramov and Foxby [Reference Avramov and Foxby1, cor. 4.2(b)(I)]. It then follows from [Reference Holm and Jørgensen14, prop. 3.12(b)] that $\mathrm {id}_\mathcal {C} X^\natural \leqslant {\rm fd}_\mathbb {k} A$![]() .
.
(c). Write $X = {\rm colim}_iP_i$![]() with each $P_i \in \mathsf {Prj}(\mathcal {C},\,A)$
with each $P_i \in \mathsf {Prj}(\mathcal {C},\,A)$![]() . Then $X^\natural = {\rm colim}_iP_i^\natural$
. Then $X^\natural = {\rm colim}_iP_i^\natural$![]() . By statement (a), one has that ${\rm pd}_\mathcal {C}(P_i^\natural ) \leqslant {\rm pd}_\mathbb {k} A$
. By statement (a), one has that ${\rm pd}_\mathcal {C}(P_i^\natural ) \leqslant {\rm pd}_\mathbb {k} A$![]() for each $i$
for each $i$![]() , so ${\rm fd}_\mathcal {C}(X^\natural ) \leqslant {\rm pd}_\mathbb {k} A$
, so ${\rm fd}_\mathcal {C}(X^\natural ) \leqslant {\rm pd}_\mathbb {k} A$![]() .
.
Lemma 1.14 Assume that $A$![]() has finite projective dimension over $\mathbb {k}$
has finite projective dimension over $\mathbb {k}$![]() . Let $X$
. Let $X$![]() be an object in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
be an object in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() . Then the following statements hold.
. Then the following statements hold.
(a) For each $G \in {_{\mathcal {C}}\mathsf {Mod}}$
 admitting an exact sequence $0 \to G \to F_{-1} \to F_{-2} \to \cdots$
admitting an exact sequence $0 \to G \to F_{-1} \to F_{-2} \to \cdots$ with each $F_i \in \mathsf {Flat}(\mathcal {C})$
with each $F_i \in \mathsf {Flat}(\mathcal {C})$ , there is an isomorphism
\[ \operatorname{Ext}_{\mathcal{C},A}^{1}\left(G \otimes_\mathbb {k} A,X\right) \cong \operatorname{Ext}_{\mathcal{C}}^{1}\left(G,X^{\natural}\right). \]
, there is an isomorphism
\[ \operatorname{Ext}_{\mathcal{C},A}^{1}\left(G \otimes_\mathbb {k} A,X\right) \cong \operatorname{Ext}_{\mathcal{C}}^{1}\left(G,X^{\natural}\right). \]
(b) For each $G \in {_{\mathcal {C}}\mathsf {Mod}}$
 admitting an exact sequence $\cdots \to I_1 \to I_0 \to G \to 0$
admitting an exact sequence $\cdots \to I_1 \to I_0 \to G \to 0$ with each $I_i \in \mathsf {Inj}(\mathcal {C})$
with each $I_i \in \mathsf {Inj}(\mathcal {C})$ , there is an isomorphism
\[ \operatorname{Ext}_{\mathcal{C},A}^{1}\left(X,\operatorname{Hom}_{\mathbb {k}}\left(A,G\right)\right) \cong \operatorname{Ext}_{\mathcal{C}}^{1}\left(X^{\natural},G\right). \]
, there is an isomorphism
\[ \operatorname{Ext}_{\mathcal{C},A}^{1}\left(X,\operatorname{Hom}_{\mathbb {k}}\left(A,G\right)\right) \cong \operatorname{Ext}_{\mathcal{C}}^{1}\left(X^{\natural},G\right). \]
Proof. By Holm and Jørgensen [Reference Holm and Jørgensen13, lem. 1.2], there is an exact sequence
Statement (a) holds after we show that $L_1(-\otimes _\mathbb {k} A)(G) = 0$![]() . For this purpose, consider the exact sequence
. For this purpose, consider the exact sequence
in ${_{\mathcal {C}}\mathsf {Mod}}$![]() with $P \in \mathsf {Prj}(\mathcal {C})$
with $P \in \mathsf {Prj}(\mathcal {C})$![]() . Clearly, $L_1(- \otimes _\mathbb {k} A)(P) = 0$
. Clearly, $L_1(- \otimes _\mathbb {k} A)(P) = 0$![]() , so it is enough to show the exactness of the sequence
, so it is enough to show the exactness of the sequence
in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() .
.
Consider the exact sequence
with each $F_i \in \mathsf {Flat}(\mathcal {C})$![]() . For each object $q$
. For each object $q$![]() in $\mathcal {C}$
in $\mathcal {C}$![]() , the sequence
, the sequence
is exact and each $F_i(q)$![]() is a flat $\mathbb {k}$
is a flat $\mathbb {k}$![]() -module by proposition 1.10(c). Since ${\rm fd}_\mathbb {k} A<\infty$
-module by proposition 1.10(c). Since ${\rm fd}_\mathbb {k} A<\infty$![]() by the assumption, one gets that $\operatorname {Tor}_{1}^{\mathbb {k}}\left (G(q),A\right ) = 0$
by the assumption, one gets that $\operatorname {Tor}_{1}^{\mathbb {k}}\left (G(q),A\right ) = 0$![]() by dimension shifting. Thus, the sequence
by dimension shifting. Thus, the sequence
is exact, which guarantees the exactness of sequence (1.14.1).
Statement (b) can be proved dually using [Reference Holm and Jørgensen13, lem. 1.3] and proposition 1.10(b), observing that ${\rm pd}_\mathbb {k} A<\infty$![]() , and $((-)^{\natural },\, \operatorname {Hom}_{\mathbb {k}}\left (A,-\right ))$
, and $((-)^{\natural },\, \operatorname {Hom}_{\mathbb {k}}\left (A,-\right ))$![]() is an adjoint pair.
is an adjoint pair.
Proposition 1.15 Assume that $A$![]() has finite projective dimension over $\mathbb {k}$
has finite projective dimension over $\mathbb {k}$![]() . Let $X$
. Let $X$![]() be an object in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
be an object in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() . If $X \in \mathsf {Cot}(\mathcal {C},\,A)$
. If $X \in \mathsf {Cot}(\mathcal {C},\,A)$![]() , then $X^\natural \in \mathsf {Cot}(\mathcal {C})$
, then $X^\natural \in \mathsf {Cot}(\mathcal {C})$![]() .
.
Proof. Take an object $F$![]() in $\mathsf {Flat}(\mathcal {C})$
in $\mathsf {Flat}(\mathcal {C})$![]() and write $F = {\rm colim}_iP_i$
and write $F = {\rm colim}_iP_i$![]() with each $P_i \in \mathsf {Prj}(\mathcal {C})$
with each $P_i \in \mathsf {Prj}(\mathcal {C})$![]() . Since the functor $- \otimes _{\mathbb {k}} A$
. Since the functor $- \otimes _{\mathbb {k}} A$![]() preserves projectives, each $P_i \otimes _{\mathbb {k}} A$
preserves projectives, each $P_i \otimes _{\mathbb {k}} A$![]() is contained in $\mathsf {Prj}(\mathcal {C},\,A)$
is contained in $\mathsf {Prj}(\mathcal {C},\,A)$![]() . Thus, $F \otimes _{\mathbb {k}} A$
. Thus, $F \otimes _{\mathbb {k}} A$![]() belongs to $\mathsf {Flat}(\mathcal {C},\,A)$
belongs to $\mathsf {Flat}(\mathcal {C},\,A)$![]() , and by lemma 1.14(a) one deduces that
, and by lemma 1.14(a) one deduces that
because $X \in \mathsf {Cot}(\mathcal {C},\,A)$![]() . Consequently, $X^\natural$
. Consequently, $X^\natural$![]() is contained in $\mathsf {Cot}(\mathcal {C})$
is contained in $\mathsf {Cot}(\mathcal {C})$![]() .
.
1.16 (Gorenstein homological objects)
Following [Reference Enochs and Jenda7], an object $X$![]() in ${_{\mathcal {C},\, A}\mathsf {Mod}}$
in ${_{\mathcal {C},\, A}\mathsf {Mod}}$![]() is called Gorenstein projective if there is an exact sequence
is called Gorenstein projective if there is an exact sequence
in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() with each $P_{i}$
with each $P_{i}$![]() projective such that $X\cong {\operatorname {Coker}(P_{1}\to P_{0})}$
projective such that $X\cong {\operatorname {Coker}(P_{1}\to P_{0})}$![]() and the sequence remains exact after applying the functor $\operatorname {Hom}_{\mathcal {C},\,A}\left (-,P\right )$
and the sequence remains exact after applying the functor $\operatorname {Hom}_{\mathcal {C},\,A}\left (-,P\right )$![]() for every projective object $P$
for every projective object $P$![]() in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() .
.
Dually, an object $X$![]() in ${_{\mathcal {C},\, A}\mathsf {Mod}}$
in ${_{\mathcal {C},\, A}\mathsf {Mod}}$![]() is called Gorenstein injective if there is an exact sequence
is called Gorenstein injective if there is an exact sequence
in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() with each $I_{i}$
with each $I_{i}$![]() injective such that $X\cong {\operatorname {Coker}(I_{1}\to I_{0})}$
injective such that $X\cong {\operatorname {Coker}(I_{1}\to I_{0})}$![]() and the sequence remains exact after applying the functor $\operatorname {Hom}_{\mathcal {C},\,A}\left (I,-\right )$
and the sequence remains exact after applying the functor $\operatorname {Hom}_{\mathcal {C},\,A}\left (I,-\right )$![]() for every injective object $I$
for every injective object $I$![]() in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() .
.
An object $X$![]() in ${_{\mathcal {C},\, A}\mathsf {Mod}}$
in ${_{\mathcal {C},\, A}\mathsf {Mod}}$![]() is called Gorenstein flat if there is an exact sequence
is called Gorenstein flat if there is an exact sequence
in ${_{\mathcal {C},\, A}\mathsf {Mod}}$![]() with each $F_{i}$
with each $F_{i}$![]() flat such that $X\cong {\operatorname {Coker}(F_{1}\to F_{0})}$
flat such that $X\cong {\operatorname {Coker}(F_{1}\to F_{0})}$![]() and the sequence remains exact after applying the functor $E\otimes _{\mathcal {C},A}-$
and the sequence remains exact after applying the functor $E\otimes _{\mathcal {C},A}-$![]() for every injective object $E$
for every injective object $E$![]() in $\mathsf {Mod}_{\mathcal {C},\,A}$
in $\mathsf {Mod}_{\mathcal {C},\,A}$![]() . Similarly, one can define projectively coresolved Gorenstein flat objects in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
. Similarly, one can define projectively coresolved Gorenstein flat objects in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() when flat objects in the above exact sequence are replaced by projective objects; see [Reference Šaroch and Št'ovíček22].
when flat objects in the above exact sequence are replaced by projective objects; see [Reference Šaroch and Št'ovíček22].
Let $\mathsf {GP}(\mathcal {C},\,A)$![]() (resp., $\mathsf {GI}(\mathcal {C},\,A)$
(resp., $\mathsf {GI}(\mathcal {C},\,A)$![]() , $\mathsf {GF}(\mathcal {C},\,A)$
, $\mathsf {GF}(\mathcal {C},\,A)$![]() , $\mathsf {PGF}(\mathcal {C},\,A)$
, $\mathsf {PGF}(\mathcal {C},\,A)$![]() ) be the subcategory of Gorenstein projective objects (resp., Gorenstein injective objects, Gorenstein flat objects, projectively coresolved Gorenstein flat objects) in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
) be the subcategory of Gorenstein projective objects (resp., Gorenstein injective objects, Gorenstein flat objects, projectively coresolved Gorenstein flat objects) in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() . In the case that $A=\mathbb {k}$
. In the case that $A=\mathbb {k}$![]() , we write $\mathsf {GP}(\mathcal {C})$
, we write $\mathsf {GP}(\mathcal {C})$![]() (resp., $\mathsf {GI}(\mathcal {C})$
(resp., $\mathsf {GI}(\mathcal {C})$![]() , $\mathsf {GF}(\mathcal {C})$
, $\mathsf {GF}(\mathcal {C})$![]() , $\mathsf {PGF}(\mathcal {C})$
, $\mathsf {PGF}(\mathcal {C})$![]() ) instead of $\mathsf {GP}(\mathcal {C},\,A)$
) instead of $\mathsf {GP}(\mathcal {C},\,A)$![]() (resp., $\mathsf {GI}(\mathcal {C},\,A)$
(resp., $\mathsf {GI}(\mathcal {C},\,A)$![]() , $\mathsf {GF}(\mathcal {C},\,A)$
, $\mathsf {GF}(\mathcal {C},\,A)$![]() , $\mathsf {PGF}(\mathcal {C},\,A)$
, $\mathsf {PGF}(\mathcal {C},\,A)$![]() ).
).
2. Model structures on ${_{\mathcal {C},\,A}\mathsf {Mod}}$
In this section we describe projective, injective and flat model structures on the category ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() , and in particular prove theorem A in the introduction. Throughout this section, we assume that $A$
, and in particular prove theorem A in the introduction. Throughout this section, we assume that $A$![]() is an associative $\mathbb {k}$
is an associative $\mathbb {k}$![]() -algebra with ${\rm pd}_\mathbb {k} A<\infty$
-algebra with ${\rm pd}_\mathbb {k} A<\infty$![]() .
.
The next result is from (the proofs of) [Reference Šaroch and Št'ovíček22, thms. 4.9, 4.11 and 5.6, and cor 4.12]; Šaroch and Št'ovíček proved it for modules over rings, but their techniques also work well for objects in ${_{\mathcal {C}}\mathsf {Mod}}$![]() (see [Reference Šaroch and Št'ovíček22, pp. 4]).
(see [Reference Šaroch and Št'ovíček22, pp. 4]).
Lemma 2.1 The following statements hold.
(a) The pair $(\mathsf {PGF}(\mathcal {C}),\, {\mathsf {PGF}(\mathcal {C})}^\perp )$
 is a complete hereditary cotorsion pair generated by a set such that ${\mathsf {PGF}(\mathcal {C})}^\perp$
is a complete hereditary cotorsion pair generated by a set such that ${\mathsf {PGF}(\mathcal {C})}^\perp$ is thick and $\mathsf {PGF}(\mathcal {C}) \cap {\mathsf {PGF}(\mathcal {C})}^\perp = \mathsf {Prj}(\mathcal {C})$
is thick and $\mathsf {PGF}(\mathcal {C}) \cap {\mathsf {PGF}(\mathcal {C})}^\perp = \mathsf {Prj}(\mathcal {C})$ .
.(b) The pair $(^{\perp }\mathsf {GI}(\mathcal {C}),\, \mathsf {GI}(\mathcal {C}))$
 is a complete hereditary cotorsion pair generated by a set such that $^{\perp }\mathsf {GI}(\mathcal {C})$
is a complete hereditary cotorsion pair generated by a set such that $^{\perp }\mathsf {GI}(\mathcal {C})$ is thick and closed under filtered colimits, and $^{\perp }\mathsf {GI}(\mathcal {C}) \cap \mathsf {GI}(\mathcal {C}) = \mathsf {Inj}(\mathcal {C})$
is thick and closed under filtered colimits, and $^{\perp }\mathsf {GI}(\mathcal {C}) \cap \mathsf {GI}(\mathcal {C}) = \mathsf {Inj}(\mathcal {C})$ .
.(c) The pair $(\mathsf {GF}(\mathcal {C}),\, {\mathsf {GF}(\mathcal {C})}^\perp )$
 is a complete hereditary cotorsion pair generated by a set such that ${\mathsf {GF}(\mathcal {C})}^\perp = \mathsf {Cot}(\mathcal {C}) \cap {\mathsf {PGF}(\mathcal {C})}^\perp$
is a complete hereditary cotorsion pair generated by a set such that ${\mathsf {GF}(\mathcal {C})}^\perp = \mathsf {Cot}(\mathcal {C}) \cap {\mathsf {PGF}(\mathcal {C})}^\perp$ and $\mathsf {GF}(\mathcal {C})\cap \mathsf {PGF}(\mathcal {C})^\perp =\mathsf {Flat}(\mathcal {C})$
and $\mathsf {GF}(\mathcal {C})\cap \mathsf {PGF}(\mathcal {C})^\perp =\mathsf {Flat}(\mathcal {C})$ , and so $\mathsf {GF}(\mathcal {C}) \cap {\mathsf {GF}(\mathcal {C})}^\perp = \mathsf {Flat}(\mathcal {C}) \cap \mathsf {Cot}(\mathcal {C})$
, and so $\mathsf {GF}(\mathcal {C}) \cap {\mathsf {GF}(\mathcal {C})}^\perp = \mathsf {Flat}(\mathcal {C}) \cap \mathsf {Cot}(\mathcal {C})$ .
.
In what follows, we set
The next result gives a projective model structure on ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() , which will then be used to construct a flat model structure.
, which will then be used to construct a flat model structure.
Proposition 2.2 The pair $(^{\perp }\mathsf {E},\, \mathsf {E})$![]() is a hereditary projective cotorsion pair in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
is a hereditary projective cotorsion pair in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() generated by a set. Moreover, there is a hereditary abelian model structure $(^{\perp }\mathsf {E},\, \mathsf {E},\, {_{\mathcal {C},\,A}\mathsf {Mod}})$
generated by a set. Moreover, there is a hereditary abelian model structure $(^{\perp }\mathsf {E},\, \mathsf {E},\, {_{\mathcal {C},\,A}\mathsf {Mod}})$![]() on ${_{\mathcal {C},\,A}\mathsf {Mod}}$
on ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() , where $^{\perp }\mathsf {E}$
, where $^{\perp }\mathsf {E}$![]() is the subcategory of cofibrant objects, $\mathsf {E}$
is the subcategory of cofibrant objects, $\mathsf {E}$![]() is the subcategory of trivial objects, and all objects in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
is the subcategory of trivial objects, and all objects in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() are fibrant objects.
are fibrant objects.
Proof. It follows from lemma 1.14(a) that $\mathsf {E} = \{ G \otimes _\mathbb {k} A\ |\ G \in \mathsf {PGF}(\mathcal {C})\}^\perp$![]() , so $(^{\perp }\mathsf {E},\, \mathsf {E})$
, so $(^{\perp }\mathsf {E},\, \mathsf {E})$![]() is a cotorsion pair in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
is a cotorsion pair in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() ; see 1.1. It is clear that $(^{\perp }\mathsf {E},\, \mathsf {E})$
; see 1.1. It is clear that $(^{\perp }\mathsf {E},\, \mathsf {E})$![]() is hereditary as $\mathsf {E}$
is hereditary as $\mathsf {E}$![]() is closed under cokernels of monomorphisms. By lemma 2.1(a), the cotorsion pair $(\mathsf {PGF}(\mathcal {C}),\, {\mathsf {PGF}(\mathcal {C})}^\perp )$
is closed under cokernels of monomorphisms. By lemma 2.1(a), the cotorsion pair $(\mathsf {PGF}(\mathcal {C}),\, {\mathsf {PGF}(\mathcal {C})}^\perp )$![]() is generated by a set $\mathsf {S}$
is generated by a set $\mathsf {S}$![]() , that is, $\mathsf {S} \subseteq \mathsf {PGF}(\mathcal {C})$
, that is, $\mathsf {S} \subseteq \mathsf {PGF}(\mathcal {C})$![]() and $\mathsf {S}^\perp = {\mathsf {PGF}(\mathcal {C})}^\perp$
and $\mathsf {S}^\perp = {\mathsf {PGF}(\mathcal {C})}^\perp$![]() . One deduces that $\{G\otimes _\mathbb {k} A\ | G\in \mathsf {S}\}^\perp = \mathsf {E}$
. One deduces that $\{G\otimes _\mathbb {k} A\ | G\in \mathsf {S}\}^\perp = \mathsf {E}$![]() again by proposition 1.14(a). Consequently, the cotorsion pair $(^{\perp }\mathsf {E},\, \mathsf {E})$
again by proposition 1.14(a). Consequently, the cotorsion pair $(^{\perp }\mathsf {E},\, \mathsf {E})$![]() is generated by a set, so $(^{\perp }\mathsf {E},\, \mathsf {E})$
is generated by a set, so $(^{\perp }\mathsf {E},\, \mathsf {E})$![]() is complete; see e.g. Göbel and Trlifaj [Reference Göbel and Trlifaj11, thm. 6.11(b)]. Since the subcategory ${\mathsf {PGF}(\mathcal {C})}^\perp$
is complete; see e.g. Göbel and Trlifaj [Reference Göbel and Trlifaj11, thm. 6.11(b)]. Since the subcategory ${\mathsf {PGF}(\mathcal {C})}^\perp$![]() is thick by lemma 2.1(a), so is $\mathsf {E}$
is thick by lemma 2.1(a), so is $\mathsf {E}$![]() clearly.
clearly.
We prove that $\mathsf {E}$![]() contains the projective objects, which implies that $(^{\perp }\mathsf {E},\, \mathsf {E})$
contains the projective objects, which implies that $(^{\perp }\mathsf {E},\, \mathsf {E})$![]() is a projective cotorsion pair in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
is a projective cotorsion pair in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() by [Reference Gillespie10, prop. 3.7]. For each $X \in \mathsf {Prj}(\mathcal {C},\,A)$
by [Reference Gillespie10, prop. 3.7]. For each $X \in \mathsf {Prj}(\mathcal {C},\,A)$![]() , one has ${\rm pd}_\mathcal {C} X^{\natural }<\infty$
, one has ${\rm pd}_\mathcal {C} X^{\natural }<\infty$![]() by proposition 1.13(a). It follows from lemma 2.1(a) that $\operatorname {Ext}_{\mathcal {C}}^{i}\left (G,P\right ) = 0$
by proposition 1.13(a). It follows from lemma 2.1(a) that $\operatorname {Ext}_{\mathcal {C}}^{i}\left (G,P\right ) = 0$![]() for each $G \in \mathsf {PGF}(\mathcal {C})$
for each $G \in \mathsf {PGF}(\mathcal {C})$![]() , $P \in \mathsf {Prj}(\mathcal {C})$
, $P \in \mathsf {Prj}(\mathcal {C})$![]() and $i \geqslant 1$
and $i \geqslant 1$![]() , so by dimension shifting one concludes that $X^{\natural }$
, so by dimension shifting one concludes that $X^{\natural }$![]() is in $\mathsf {PGF}(\mathcal {C})^\perp$
is in $\mathsf {PGF}(\mathcal {C})^\perp$![]() . Thus, one has $X\in \mathsf {E}$
. Thus, one has $X\in \mathsf {E}$![]() , as desired.
, as desired.
We then give an injective model structure on ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() . Set
. Set
Proposition 2.3 The pair $(\mathsf {T},\, \mathsf {T}^\perp )$![]() is a hereditary cotorsion pair in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
is a hereditary cotorsion pair in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() such that $\mathsf {T}$
such that $\mathsf {T}$![]() is thick and contains injective objects. If furthermore the subcategory $^\perp \mathsf {GI}(\mathcal {C})$
is thick and contains injective objects. If furthermore the subcategory $^\perp \mathsf {GI}(\mathcal {C})$![]() is closed under pure quotients, then $(\mathsf {T},\, \mathsf {T}^\perp )$
is closed under pure quotients, then $(\mathsf {T},\, \mathsf {T}^\perp )$![]() is an injective perfect cotorsion pair. In this case, there is a hereditary abelian model structure $({_{\mathcal {C},\,A}\mathsf {Mod}},\, \mathsf {T},\, \mathsf {T}^\perp )$
is an injective perfect cotorsion pair. In this case, there is a hereditary abelian model structure $({_{\mathcal {C},\,A}\mathsf {Mod}},\, \mathsf {T},\, \mathsf {T}^\perp )$![]() on ${_{\mathcal {C},\,A}\mathsf {Mod}}$
on ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() , where $\mathsf {T}^\perp$
, where $\mathsf {T}^\perp$![]() is the subcategory of fibrant objects, $\mathsf {T}$
is the subcategory of fibrant objects, $\mathsf {T}$![]() is the subcategory of trivial objects and all objects in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
is the subcategory of trivial objects and all objects in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() are cofibrant objects.
are cofibrant objects.
Proof. By lemma 1.14(b), one has $\mathsf {T} = {^\perp \{\operatorname {Hom}_{\mathbb {k}}\left (A,G\right )\ | \ G \in \mathsf {GI}(\mathcal {C})\}}$![]() , so $(\mathsf {T},\, \mathsf {T}^\perp )$
, so $(\mathsf {T},\, \mathsf {T}^\perp )$![]() is a cotorsion pair in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
is a cotorsion pair in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() ; it is hereditary as $\mathsf {T}$
; it is hereditary as $\mathsf {T}$![]() is closed under kernels of epimorphisms. It is clear that the subcategory $\mathsf {T}$
is closed under kernels of epimorphisms. It is clear that the subcategory $\mathsf {T}$![]() is thick since ${^\perp \mathsf {GI}(\mathcal {C})}$
is thick since ${^\perp \mathsf {GI}(\mathcal {C})}$![]() is thick by lemma 2.1(b). For each $X \in \mathsf {Inj}(\mathcal {C},\,A)$
is thick by lemma 2.1(b). For each $X \in \mathsf {Inj}(\mathcal {C},\,A)$![]() , one has $\mathrm {id}_\mathcal {C} X^{\natural }<\infty$
, one has $\mathrm {id}_\mathcal {C} X^{\natural }<\infty$![]() by proposition 1.13(b). It follows from lemma 2.1(b) that $\operatorname {Ext}_{\mathcal {C}}^{i}\left (I,G\right ) = 0$
by proposition 1.13(b). It follows from lemma 2.1(b) that $\operatorname {Ext}_{\mathcal {C}}^{i}\left (I,G\right ) = 0$![]() for each $G \in \mathsf {GI}(\mathcal {C})$
for each $G \in \mathsf {GI}(\mathcal {C})$![]() , $I \in \mathsf {Inj}(\mathcal {C})$
, $I \in \mathsf {Inj}(\mathcal {C})$![]() and $i \geqslant 1$
and $i \geqslant 1$![]() , so by dimension shifting one gets that $X^{\natural }$
, so by dimension shifting one gets that $X^{\natural }$![]() is in $^\perp \mathsf {GI}(\mathcal {C})$
is in $^\perp \mathsf {GI}(\mathcal {C})$![]() . Thus, one has $X \in \mathsf {T}$
. Thus, one has $X \in \mathsf {T}$![]() , and hence $\mathsf {T}$
, and hence $\mathsf {T}$![]() contains all injective objects in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
contains all injective objects in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() .
.
Now we assume that the subcategory $^\perp \mathsf {GI}(\mathcal {C})$![]() is closed under pure quotients. Then $^\perp \mathsf {GI}(\mathcal {C})$
is closed under pure quotients. Then $^\perp \mathsf {GI}(\mathcal {C})$![]() is also closed under pure submodules since $(^{\perp }\mathsf {GI}(\mathcal {C}),\,\mathsf {GI}(\mathcal {C}))$
is also closed under pure submodules since $(^{\perp }\mathsf {GI}(\mathcal {C}),\,\mathsf {GI}(\mathcal {C}))$![]() is a hereditary cotorsion pair by lemma 2.1(b). The forgetful functor $(-)^{\natural }$
is a hereditary cotorsion pair by lemma 2.1(b). The forgetful functor $(-)^{\natural }$![]() preserves colimits and pure exact sequence by [Reference Holm and Jørgensen14, lem. 5.7]. It follows that the subcategory $\mathsf {T}$
preserves colimits and pure exact sequence by [Reference Holm and Jørgensen14, lem. 5.7]. It follows that the subcategory $\mathsf {T}$![]() is closed under pure submodules and pure quotients, and furthermore is closed under filtered colimits since the subcategory $^\perp \mathsf {GI}(\mathcal {C})$
is closed under pure submodules and pure quotients, and furthermore is closed under filtered colimits since the subcategory $^\perp \mathsf {GI}(\mathcal {C})$![]() is closed under filtered colimits by lemma 2.1(b). Thus by [Reference Holm and Jørgensen14, thm. A.3], the cotorsion pair $(\mathsf {T},\, \mathsf {T}^\perp )$
is closed under filtered colimits by lemma 2.1(b). Thus by [Reference Holm and Jørgensen14, thm. A.3], the cotorsion pair $(\mathsf {T},\, \mathsf {T}^\perp )$![]() is perfect. Moreover, by [Reference Gillespie10, prop. 3.6], $(\mathsf {T},\, \mathsf {T}^\perp )$
is perfect. Moreover, by [Reference Gillespie10, prop. 3.6], $(\mathsf {T},\, \mathsf {T}^\perp )$![]() is an injective cotorsion pair.
is an injective cotorsion pair.
In the following we give a flat model structure on ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() . For this purpose, we first prove the next lemma.
. For this purpose, we first prove the next lemma.
Lemma 2.4 The pair $(^{\perp }(\mathsf {Cot}(\mathcal {C},\,A)\cap \mathsf {E}),\, \mathsf {Cot}(\mathcal {C},\,A)\cap \mathsf {E})$![]() is a complete and hereditary cotorsion pair in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
is a complete and hereditary cotorsion pair in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() generated by a set, and $^{\perp }(\mathsf {Cot}(\mathcal {C},\,A)\cap \mathsf {E})\cap \mathsf {E}=\mathsf {Flat}(\mathcal {C},\,A)$
generated by a set, and $^{\perp }(\mathsf {Cot}(\mathcal {C},\,A)\cap \mathsf {E})\cap \mathsf {E}=\mathsf {Flat}(\mathcal {C},\,A)$![]() .
.
Proof. By proposition 2.2, there is a set $\mathsf {S} \subseteq {^\perp \mathsf {E}}$![]() such that $\mathsf {S}^\perp = \mathsf {E}$
such that $\mathsf {S}^\perp = \mathsf {E}$![]() . On the other hand, the cotorsion pair $(\mathsf {Flat}(\mathcal {C},\,A),\, \mathsf {Cot}(\mathcal {C},\,A))$
. On the other hand, the cotorsion pair $(\mathsf {Flat}(\mathcal {C},\,A),\, \mathsf {Cot}(\mathcal {C},\,A))$![]() is generated by a set $\mathsf {R}$
is generated by a set $\mathsf {R}$![]() (see 1.5), that is, $\mathsf {R} \subseteq \mathsf {Flat}(\mathcal {C},\,A)$
(see 1.5), that is, $\mathsf {R} \subseteq \mathsf {Flat}(\mathcal {C},\,A)$![]() and $\mathsf {R}^\perp = \mathsf {Cot}(\mathcal {C},\,A)$
and $\mathsf {R}^\perp = \mathsf {Cot}(\mathcal {C},\,A)$![]() . Thus, one has
. Thus, one has
which implies that $(^{\perp }(\mathsf {Cot}(\mathcal {C},\,A) \cap \mathsf {E}),\, \mathsf {Cot}(\mathcal {C},\,A) \cap \mathsf {E})$![]() is a complete cotorsion pair in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
is a complete cotorsion pair in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() generated by a set; see [Reference Göbel and Trlifaj11, thm. 6.11(b)]. The subcategory $\mathsf {Cot}(\mathcal {C},\,A) \cap \mathsf {E}$
generated by a set; see [Reference Göbel and Trlifaj11, thm. 6.11(b)]. The subcategory $\mathsf {Cot}(\mathcal {C},\,A) \cap \mathsf {E}$![]() is closed under cokernels of monomorphisms as so are $\mathsf {Cot}(\mathcal {C},\,A)$
is closed under cokernels of monomorphisms as so are $\mathsf {Cot}(\mathcal {C},\,A)$![]() and $\mathsf {E}$
and $\mathsf {E}$![]() by proposition 2.2. Thus, the cotorsion pair
by proposition 2.2. Thus, the cotorsion pair
is hereditary.
We next prove the equality $^{\perp }(\mathsf {Cot}(\mathcal {C},\,A) \cap \mathsf {E}) \cap \mathsf {E} = \mathsf {Flat}(\mathcal {C},\,A)$![]() . It is clear that $\mathsf {Flat}(\mathcal {C},\,A) = {^{\perp }\mathsf {Cot}(\mathcal {C},\,A)} \subseteq {^{\perp }(\mathsf {Cot}(\mathcal {C},\,A) \cap \mathsf {E})}$
. It is clear that $\mathsf {Flat}(\mathcal {C},\,A) = {^{\perp }\mathsf {Cot}(\mathcal {C},\,A)} \subseteq {^{\perp }(\mathsf {Cot}(\mathcal {C},\,A) \cap \mathsf {E})}$![]() . On the other hand, if $X \in \mathsf {Flat}(\mathcal {C},\,A)$
. On the other hand, if $X \in \mathsf {Flat}(\mathcal {C},\,A)$![]() , then $X^{\natural }$
, then $X^{\natural }$![]() has finite flat dimension in ${_{\mathcal {C}}\mathsf {Mod}}$
has finite flat dimension in ${_{\mathcal {C}}\mathsf {Mod}}$![]() by lemma 1.13(c), and so it follows from [Reference Šaroch and Št'ovíček22, thm. 4.11] that $X^{\natural }$
by lemma 1.13(c), and so it follows from [Reference Šaroch and Št'ovíček22, thm. 4.11] that $X^{\natural }$![]() is in $\mathsf {PGF}(\mathcal {C})^\perp$
is in $\mathsf {PGF}(\mathcal {C})^\perp$![]() . This implies that $X$
. This implies that $X$![]() is in $\mathsf {E}$
is in $\mathsf {E}$![]() . Thus, one has
. Thus, one has
To prove the inclusion of the other direction, we take an arbitrary
Since $(\mathsf {Flat}(\mathcal {C},\,A),\, \mathsf {Cot}(\mathcal {C},\,A))$![]() is a complete cotorsion pair (see 1.5), there is an exact sequence
is a complete cotorsion pair (see 1.5), there is an exact sequence
with $C \in \mathsf {Cot}(\mathcal {C},\,A)$![]() and $F \in \mathsf {Flat}(\mathcal {C},\,A) \subseteq \mathsf {E}$
and $F \in \mathsf {Flat}(\mathcal {C},\,A) \subseteq \mathsf {E}$![]() as proved before. Thus, $C$
as proved before. Thus, $C$![]() is contained in $\mathsf {E}$
is contained in $\mathsf {E}$![]() as $\mathsf {E}$
as $\mathsf {E}$![]() is thick by proposition 2.2, so $\operatorname {Ext}_{\mathcal {C},\,A}^{1}\left (Y,C\right )=0$
is thick by proposition 2.2, so $\operatorname {Ext}_{\mathcal {C},\,A}^{1}\left (Y,C\right )=0$![]() . Consequently, sequence (2.4.1) splits, and so $Y$
. Consequently, sequence (2.4.1) splits, and so $Y$![]() belongs to $\mathsf {Flat}(\mathcal {C},\,A)$
belongs to $\mathsf {Flat}(\mathcal {C},\,A)$![]() .
.
Now we are in a position to give the main result in this section.
Theorem 2.5 There is a hereditary abelian model structure
on ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() , where $^{\perp }(\mathsf {Cot}(\mathcal {C},\,A)\cap \mathsf {E})$
, where $^{\perp }(\mathsf {Cot}(\mathcal {C},\,A)\cap \mathsf {E})$![]() is the subcategory of cofibrant objects, $\mathsf {E}$
is the subcategory of cofibrant objects, $\mathsf {E}$![]() is the subcategory of trivial objects and $\mathsf {Cot}(\mathcal {C},\,A)$
is the subcategory of trivial objects and $\mathsf {Cot}(\mathcal {C},\,A)$![]() is the subcategory of fibrant objects.
is the subcategory of fibrant objects.
Proof. We mention that $(\mathsf {Flat}(\mathcal {C},\,A),\, \mathsf {Cot}(\mathcal {C},\,A))$![]() is a complete and hereditary cotorsion pair in ${_{\mathcal {C},\,A}\mathsf {Mod}}$
is a complete and hereditary cotorsion pair in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() ; see 1.5. Thus, by Gillespie [Reference Gillespie9, thm. 1.1] and lemma 2.4, there is a hereditary abelian model structure
; see 1.5. Thus, by Gillespie [Reference Gillespie9, thm. 1.1] and lemma 2.4, there is a hereditary abelian model structure
on ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() , where the subcategory $\mathsf {W}$
, where the subcategory $\mathsf {W}$![]() can be described as follows:
can be described as follows:
We then prove that there is an equality $\mathsf {W}=\mathsf {E}$![]() .
.
Take an object $X\in \mathsf {W}$![]() . Then there is an exact sequence
. Then there is an exact sequence
in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() with $U\in \mathsf {Cot}(\mathcal {C},\,A)\cap \mathsf {E}$
with $U\in \mathsf {Cot}(\mathcal {C},\,A)\cap \mathsf {E}$![]() and $F\in \mathsf {Flat}(\mathcal {C},\,A)$
and $F\in \mathsf {Flat}(\mathcal {C},\,A)$![]() . Thus, the sequence
. Thus, the sequence
is exact, where $U^{\natural }\in \mathsf {PGF}(\mathcal {C})^\perp$![]() and $F^{\natural }$
and $F^{\natural }$![]() has finite flat dimension by proposition 1.13(c). So it is easy to check that $F^{\natural }$
has finite flat dimension by proposition 1.13(c). So it is easy to check that $F^{\natural }$![]() is in $\mathsf {PGF}(\mathcal {C})^\perp$
is in $\mathsf {PGF}(\mathcal {C})^\perp$![]() as $\mathsf {Flat}(\mathcal {C})\subseteq \mathsf {PGF}(\mathcal {C})^\perp$
as $\mathsf {Flat}(\mathcal {C})\subseteq \mathsf {PGF}(\mathcal {C})^\perp$![]() by lemma 2.1(c). The subcategory $\mathsf {PGF}(\mathcal {C})^\perp$
by lemma 2.1(c). The subcategory $\mathsf {PGF}(\mathcal {C})^\perp$![]() is thick by lemma 2.1(a), so $X^{\natural }$
is thick by lemma 2.1(a), so $X^{\natural }$![]() is in $\mathsf {PGF}(\mathcal {C})^\perp$
is in $\mathsf {PGF}(\mathcal {C})^\perp$![]() . This implies that $X$
. This implies that $X$![]() is in $\mathsf {E}$
is in $\mathsf {E}$![]() . To prove the inclusion of the other direction, we take an object $Y\in \mathsf {E}$
. To prove the inclusion of the other direction, we take an object $Y\in \mathsf {E}$![]() . By the completeness of the cotorsion pair $(\mathsf {Flat}(\mathcal {C},\,A),\, \mathsf {Cot}(\mathcal {C},\,A))$
. By the completeness of the cotorsion pair $(\mathsf {Flat}(\mathcal {C},\,A),\, \mathsf {Cot}(\mathcal {C},\,A))$![]() , there is an exact sequence
, there is an exact sequence
in ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() with $U'\in \mathsf {Cot}(\mathcal {C},\,A)$
with $U'\in \mathsf {Cot}(\mathcal {C},\,A)$![]() and $F'\in \mathsf {Flat}(\mathcal {C},\,A)$
and $F'\in \mathsf {Flat}(\mathcal {C},\,A)$![]() . Consider the exact sequence
. Consider the exact sequence
in ${_{\mathcal {C}}\mathsf {Mod}}$![]() . The object $(F')^{\natural }$
. The object $(F')^{\natural }$![]() has finite flat dimension by proposition 1.13(c), and so it is in $\mathsf {PGF}(\mathcal {C})^\perp$
has finite flat dimension by proposition 1.13(c), and so it is in $\mathsf {PGF}(\mathcal {C})^\perp$![]() as proved before. On the other hand, $Y^{\natural }$
as proved before. On the other hand, $Y^{\natural }$![]() is in $\mathsf {PGF}(\mathcal {C})^\perp$
is in $\mathsf {PGF}(\mathcal {C})^\perp$![]() as $Y\in \mathsf {E}$
as $Y\in \mathsf {E}$![]() . Thus, by lemma 2.1(a), one has $(U')^{\natural }\in \mathsf {PGF}(\mathcal {C})^\perp$
. Thus, by lemma 2.1(a), one has $(U')^{\natural }\in \mathsf {PGF}(\mathcal {C})^\perp$![]() , and so $U'$
, and so $U'$![]() is in $\mathsf {E}$
is in $\mathsf {E}$![]() . This implies that $Y$
. This implies that $Y$![]() is in $\mathsf {W}$
is in $\mathsf {W}$![]() .
.
Now one gets a hereditary abelian model structure
on ${_{\mathcal {C},\,A}\mathsf {Mod}}$![]() , as desired.
, as desired.
Setup 2.6 In the rest of this section we let $\mathcal {Q}$![]() be a small $\mathbb {k}$
be a small $\mathbb {k}$![]() -linear category satisfying the following self-dual conditions specified in [Reference Holm and Jørgensen14, Setup 2.5]:
-linear category satisfying the following self-dual conditions specified in [Reference Holm and Jørgensen14, Setup 2.5]:
(1) Each $\mathbb {k}$
 -module $\mathcal {Q}(p,\,q)$
-module $\mathcal {Q}(p,\,q)$ is finitely generated and projective.
is finitely generated and projective.(2) $\mathcal {Q}$
 satisfies the local boundedness, that is for any object $q$
satisfies the local boundedness, that is for any object $q$ in $\mathcal {Q}$
in $\mathcal {Q}$ , there are only finitely many objects in $\mathcal {Q}$
, there are only finitely many objects in $\mathcal {Q}$ mapping nontrivially into or out of $q$
mapping nontrivially into or out of $q$ .
.(3) There exists a Serre functor, that is a $\mathbb {k}$
 -linear auto-equivalence $\mathbb {S}: \mathcal {Q} \to \mathcal {Q}$
-linear auto-equivalence $\mathbb {S}: \mathcal {Q} \to \mathcal {Q}$ such that $\mathcal {Q}(p,\,q)\cong \operatorname {Hom}_{\mathbb {k}}\left (\mathcal {Q}(q,\,\mathbb {S}(p)),\mathbb {k}\right ).$
such that $\mathcal {Q}(p,\,q)\cong \operatorname {Hom}_{\mathbb {k}}\left (\mathcal {Q}(q,\,\mathbb {S}(p)),\mathbb {k}\right ).$
(4) For any object $q$
 in $\mathcal {Q}$
in $\mathcal {Q}$ , the unit map $\mathbb {k}\to \mathcal {Q}(q,\,q)$
, the unit map $\mathbb {k}\to \mathcal {Q}(q,\,q)$ (via $x\mapsto x\cdot \mathrm {id}_q$
(via $x\mapsto x\cdot \mathrm {id}_q$ ) has a $\mathbb {k}$
) has a $\mathbb {k}$ -module retraction; whence there is a $\mathbb {k}$
-module retraction; whence there is a $\mathbb {k}$ -module decomposition $\mathcal {Q}(q,\,q)=\mathbb {k}\cdot \mathrm {id}_q\oplus \tau _q$
-module decomposition $\mathcal {Q}(q,\,q)=\mathbb {k}\cdot \mathrm {id}_q\oplus \tau _q$ .
.
Remark 2.7 If $\mathbb {k}$![]() is Gorenstein, then it follows from Dell'Ambrogio, Stevenson and Šťovíček [Reference Dell'Ambrogio, Stevenson and Šťovíček4, thm. 1.6] that ${_{\mathcal {Q}}\mathsf {Mod}}$
is Gorenstein, then it follows from Dell'Ambrogio, Stevenson and Šťovíček [Reference Dell'Ambrogio, Stevenson and Šťovíček4, thm. 1.6] that ${_{\mathcal {Q}}\mathsf {Mod}}$![]() is a locally Gorenstein category in the sense of Enochs, Estrada and García Rozas [Reference Enochs, Estrada and García Rozas5], and so it is easy to check that all Gorenstein projective objects in ${_{\mathcal {Q}}\mathsf {Mod}}$
is a locally Gorenstein category in the sense of Enochs, Estrada and García Rozas [Reference Enochs, Estrada and García Rozas5], and so it is easy to check that all Gorenstein projective objects in ${_{\mathcal {Q}}\mathsf {Mod}}$![]() are Gorenstein flat. Thus, the subcategory $\mathsf {PGF}(\mathcal {Q})$
are Gorenstein flat. Thus, the subcategory $\mathsf {PGF}(\mathcal {Q})$![]() coincides with the subcategory $\mathsf {GP}(\mathcal {Q})$
coincides with the subcategory $\mathsf {GP}(\mathcal {Q})$![]() ; see the remark after [Reference Šaroch and Št'ovíček22, exa. 4.10]. In this case, proposition 2.2 recovers [Reference Holm and Jørgensen14, thms. 5.5 and 6.1(a)].
; see the remark after [Reference Šaroch and Št'ovíček22, exa. 4.10]. In this case, proposition 2.2 recovers [Reference Holm and Jørgensen14, thms. 5.5 and 6.1(a)].
In proposition 2.3, we describe the injective model structure under the assumption that the subcategory $^\perp \mathsf {GI}(\mathcal {C})$![]() is closed under pure quotients. We mention that the question whether $^\perp \mathsf {GI}(\mathcal {C})$
is closed under pure quotients. We mention that the question whether $^\perp \mathsf {GI}(\mathcal {C})$![]() is closed under pure quotients remains open; see [Reference Šaroch and Št'ovíček22, pp. 31]. However, for the $\mathbb {k}$
is closed under pure quotients remains open; see [Reference Šaroch and Št'ovíček22, pp. 31]. However, for the $\mathbb {k}$![]() -linear category $\mathcal {Q}$
-linear category $\mathcal {Q}$![]() , if $\mathbb {k}$
, if $\mathbb {k}$![]() is $n$
is $n$![]() -Gorenstein, then by [Reference Dell'Ambrogio, Stevenson and Šťovíček4, thm. 1.6], ${_{\mathcal {Q}}\mathsf {Mod}}$
-Gorenstein, then by [Reference Dell'Ambrogio, Stevenson and Šťovíček4, thm. 1.6], ${_{\mathcal {Q}}\mathsf {Mod}}$![]() is a locally $n$
is a locally $n$![]() -Gorenstein category, so $^\perp \mathsf {GI}(\mathcal {Q})$
-Gorenstein category, so $^\perp \mathsf {GI}(\mathcal {Q})$![]() is actually the subcategory of objects with finite injective dimension at most $n$
is actually the subcategory of objects with finite injective dimension at most $n$![]() . Thus, $^\perp \mathsf {GI}(\mathcal {Q})$
. Thus, $^\perp \mathsf {GI}(\mathcal {Q})$![]() is closed under pure quotients by [Reference Holm and Jørgensen14, prop. 5.3(b) and lem. 5.6]. In this case, proposition 2.3 recovers [Reference Holm and Jørgensen14, thms. 5.9 and 6.1(b)].
is closed under pure quotients by [Reference Holm and Jørgensen14, prop. 5.3(b) and lem. 5.6]. In this case, proposition 2.3 recovers [Reference Holm and Jørgensen14, thms. 5.9 and 6.1(b)].
As described in Introduction, the following result gives a flat model structure whose homotopy category is the $\mathcal {Q}$![]() -shaped derived category introduced in [Reference Holm and Jørgensen14].
-shaped derived category introduced in [Reference Holm and Jørgensen14].
Corollary 2.8 Let $\mathcal {Q}$![]() be a small $\mathbb {k}$
be a small $\mathbb {k}$![]() -linear category satisfying the conditions in setup 2.6, and assume that $\mathbb {k}$
-linear category satisfying the conditions in setup 2.6, and assume that $\mathbb {k}$![]() is Gorenstein. Then there is a hereditary abelian model structure
is Gorenstein. Then there is a hereditary abelian model structure
on ${_{\mathcal {Q},\,A}\mathsf {Mod}}$![]() , where $\mathsf {E} \!=\! \{X \!\in\! {_{\mathcal {Q},\,A}\mathsf {Mod}}\ | X^{\natural }\ \mathrm {has\ finite\ projective\ dimension in}\ {_{\mathcal {Q}}\mathsf {Mod}}\}$
, where $\mathsf {E} \!=\! \{X \!\in\! {_{\mathcal {Q},\,A}\mathsf {Mod}}\ | X^{\natural }\ \mathrm {has\ finite\ projective\ dimension in}\ {_{\mathcal {Q}}\mathsf {Mod}}\}$![]() .
.
Proof. The model structure in the statement can be obtained by theorem 2.5. As shown in remark 2.7, ${_{\mathcal {Q}}\mathsf {Mod}}$![]() is a locally Gorenstein category, so one has
is a locally Gorenstein category, so one has
where $\mathsf {Prj}(\mathcal {Q})_{<\infty }$![]() is the subcategory of objects in ${_{\mathcal {Q}}\mathsf {Mod}}$
is the subcategory of objects in ${_{\mathcal {Q}}\mathsf {Mod}}$![]() with finite projective dimension. Thus, one gets that
with finite projective dimension. Thus, one gets that
as desired.
Remark 2.9 If we impose the following extra conditions on $\mathcal {Q}$![]() and $\mathbb {k}$
and $\mathbb {k}$![]() :
:
(5) $\mathbb {k}$
 is noetherian and hereditary;
is noetherian and hereditary;(6) $\mathcal {Q}$
 satisfies the strong retraction property, that is, the $\mathbb {k}$
satisfies the strong retraction property, that is, the $\mathbb {k}$ -submodules $\tau _q$
-submodules $\tau _q$ in setup 2.6(4) are compatible with composition in $\mathcal {Q}$
in setup 2.6(4) are compatible with composition in $\mathcal {Q}$ as follows:
\[ \tau_q \circ \tau_q \subseteq \tau_q \text{ for all objects }q,\text{ and }\mathcal{Q}(q,p) \circ \mathcal{Q}(p,q) \subseteq\tau_p \text{ for all }p \neq q; \]
as follows:
\[ \tau_q \circ \tau_q \subseteq \tau_q \text{ for all objects }q,\text{ and }\mathcal{Q}(q,p) \circ \mathcal{Q}(p,q) \subseteq\tau_p \text{ for all }p \neq q; \]
(7) the pseudo-radical $\tau$
 given in [Reference Holm and Jørgensen14, rmk. 7.4 and lem. 7.7] is nilpotent,
given in [Reference Holm and Jørgensen14, rmk. 7.4 and lem. 7.7] is nilpotent,
then there is an inclusion
Indeed, take an arbitrary $X$![]() in $^{\perp }(\mathsf {Cot}(\mathcal {Q},\,A) \cap \mathsf {E})$
in $^{\perp }(\mathsf {Cot}(\mathcal {Q},\,A) \cap \mathsf {E})$![]() , and fix an object $q$
, and fix an object $q$![]() in $\mathcal {Q}$
in $\mathcal {Q}$![]() and an object $N$
and an object $N$![]() in $\mathsf {Cot}(A)$
in $\mathsf {Cot}(A)$![]() . It follows from [Reference Holm and Jørgensen14, thm. 7.1 and lem. 7.14] that $G_q(N)$
. It follows from [Reference Holm and Jørgensen14, thm. 7.1 and lem. 7.14] that $G_q(N)$![]() is in $\mathsf {E}$
is in $\mathsf {E}$![]() , and hence in $\mathsf {Cot}(\mathcal {Q},\,A) \cap \mathsf {E}$
, and hence in $\mathsf {Cot}(\mathcal {Q},\,A) \cap \mathsf {E}$![]() by corollary 1.11. Thus, one gets that
by corollary 1.11. Thus, one gets that
by lemma 1.9, and so $X(q)$![]() belongs to $\mathsf {Flat}(A)$
belongs to $\mathsf {Flat}(A)$![]() .
.
3. Characterizations of Gorenstein objects in ${_{\mathcal {Q},\,A}\mathsf {Mod}}$
Throughout this section, we assume that $\mathcal {Q}$![]() is a small $\mathbb {k}$
is a small $\mathbb {k}$![]() -linear category satisfying conditions (1)–(3) in setup 2.6, and assume that $A$
-linear category satisfying conditions (1)–(3) in setup 2.6, and assume that $A$![]() is an associative $\mathbb {k}$
is an associative $\mathbb {k}$![]() -algebra (not necessarily has finite projective dimension). If $A$
-algebra (not necessarily has finite projective dimension). If $A$![]() is Gorenstein then it is known that an object $X$
is Gorenstein then it is known that an object $X$![]() in ${_{\mathcal {Q},\, A}\mathsf {Mod}}$
in ${_{\mathcal {Q},\, A}\mathsf {Mod}}$![]() is Gorenstein projective (resp., Gorenstein injective) if and only if each left $A$
is Gorenstein projective (resp., Gorenstein injective) if and only if each left $A$![]() -module $X(q)$
-module $X(q)$![]() is Gorenstein projective (resp., Gorenstein injective) for $q\in \mathcal {Q}$
is Gorenstein projective (resp., Gorenstein injective) for $q\in \mathcal {Q}$![]() ; see [Reference Dell'Ambrogio, Stevenson and Šťovíček4, cor. 4.8]. In this section, we show that the above result holds for an arbitrary associative $\mathbb {k}$
; see [Reference Dell'Ambrogio, Stevenson and Šťovíček4, cor. 4.8]. In this section, we show that the above result holds for an arbitrary associative $\mathbb {k}$![]() -algebra $A$
-algebra $A$![]() . We also prove that an object $X$
. We also prove that an object $X$![]() in ${_{\mathcal {Q},\, A}\mathsf {Mod}}$
in ${_{\mathcal {Q},\, A}\mathsf {Mod}}$![]() is Gorenstein flat (resp., projectively coresolved Gorenstein flat) if and only if each left $A$
is Gorenstein flat (resp., projectively coresolved Gorenstein flat) if and only if each left $A$![]() -module $X(q)$
-module $X(q)$![]() is Gorenstein flat (resp., projectively coresolved Gorenstein flat) for $q\in \mathcal {Q}$
is Gorenstein flat (resp., projectively coresolved Gorenstein flat) for $q\in \mathcal {Q}$![]() . We prove these results relying on the concept of Frobenius functors introduced by Chen and Ren in [Reference Chen and Ren2] and a main result of that paper.
. We prove these results relying on the concept of Frobenius functors introduced by Chen and Ren in [Reference Chen and Ren2] and a main result of that paper.
3.1 (Frobenius functor)
Let $F: \sf C\to \sf D$![]() and $G: \sf D \to \sf C$
and $G: \sf D \to \sf C$![]() be two additive functors between abelian categories, and let $\alpha : \sf C \to \sf C$
be two additive functors between abelian categories, and let $\alpha : \sf C \to \sf C$![]() and $\beta : \sf D \to \sf D$
and $\beta : \sf D \to \sf D$![]() be two auto-equivalences. Recall from [Reference Chen and Ren2] that $(F,\, G)$
be two auto-equivalences. Recall from [Reference Chen and Ren2] that $(F,\, G)$![]() is called a Frobenius pair (of type $(\alpha,\, \beta )$
is called a Frobenius pair (of type $(\alpha,\, \beta )$![]() ) between $\sf C$
) between $\sf C$![]() and $\sf D$
and $\sf D$![]() if both $(F,\, G)$
if both $(F,\, G)$![]() and $(G,\, \beta F\alpha )$
and $(G,\, \beta F\alpha )$![]() are adjoint pairs, and the functor $F$
are adjoint pairs, and the functor $F$![]() is said to be a Frobenius functor if it fits into a Frobenius pair $(F,\, G)$
is said to be a Frobenius functor if it fits into a Frobenius pair $(F,\, G)$![]() ; in this case $G$
; in this case $G$![]() is also a Frobenius functor.
is also a Frobenius functor.
Remark 3.2 Let $F: \sf C\to \sf D$![]() and $G: \sf D \to \sf C$
and $G: \sf D \to \sf C$![]() be two additive functors between Grothendieck categories admitting enough projectives. It is easy to see that if $(F,\, G)$
be two additive functors between Grothendieck categories admitting enough projectives. It is easy to see that if $(F,\, G)$![]() is a Frobenius pair then $F$
is a Frobenius pair then $F$![]() and $G$
and $G$![]() are exact functor preserving projectives, injectives and flats.
are exact functor preserving projectives, injectives and flats.
The next result was proved by Chen and Ren; see [Reference Chen and Ren2, thm. 3.2].
Lemma 3.3 Let $F: \sf C\to \sf D$![]() be a faithful Frobenius functor between two abelian categories admitting enough projectives. Then an object $X$
be a faithful Frobenius functor between two abelian categories admitting enough projectives. Then an object $X$![]() in $\sf C$
in $\sf C$![]() is Gorenstein projective if and only if $F(X)$
is Gorenstein projective if and only if $F(X)$![]() is Gorenstein projective in $\sf D$
is Gorenstein projective in $\sf D$![]() .
.
3.4 The product category $\prod _{q\in \mathcal {Q}}{_{A}\mathsf {Mod}}$![]() is a locally finitely presentable Grothendieck category admitting enough projectives and injectives. Let $(M_{q})_{q\in \mathcal {Q}}$
is a locally finitely presentable Grothendieck category admitting enough projectives and injectives. Let $(M_{q})_{q\in \mathcal {Q}}$![]() be an object in $\prod _{q\in \mathcal {Q}}{_{A}\mathsf {Mod}}$
be an object in $\prod _{q\in \mathcal {Q}}{_{A}\mathsf {Mod}}$![]() . Then it is clear that $(M_{q})_{q\in \mathcal {Q}}$
. Then it is clear that $(M_{q})_{q\in \mathcal {Q}}$![]() is projective (resp., injective, flat) if and only if each left $A$
is projective (resp., injective, flat) if and only if each left $A$![]() -module $M_{q}$
-module $M_{q}$![]() is projective (resp., injective, flat) for $q\in \mathcal {Q}$
is projective (resp., injective, flat) for $q\in \mathcal {Q}$![]() . Also, one can check that an object $(M_{q})_{q\in \mathcal {Q}}$
. Also, one can check that an object $(M_{q})_{q\in \mathcal {Q}}$![]() in $\prod _{q\in \mathcal {Q}}{_{A}\mathsf {Mod}}$
in $\prod _{q\in \mathcal {Q}}{_{A}\mathsf {Mod}}$![]() is Gorenstein projectiveFootnote 1 (resp., Gorenstein injective, Gorenstein flat) if and only if each left $A$
is Gorenstein projectiveFootnote 1 (resp., Gorenstein injective, Gorenstein flat) if and only if each left $A$![]() -module $M_{q}$
-module $M_{q}$![]() is Gorenstein projective (resp., Gorenstein injective, Gorenstein flat) for $q\in \mathcal {Q}$
is Gorenstein projective (resp., Gorenstein injective, Gorenstein flat) for $q\in \mathcal {Q}$![]() .
.
Lemma 3.5 There is an adjoint triple $(i^{*},\,i_{*},\,i^{!})$![]() as follows:
as follows:

Moreover, $(i_{*},\, i^{!})$![]() is a Frobenius pair. In particular, $i_{*}$
is a Frobenius pair. In particular, $i_{*}$![]() and $i^{!}$
and $i^{!}$![]() are Frobenius functors.
are Frobenius functors.
Proof. For $X\in {_{\mathcal {Q},\,A}\mathsf {Mod}}$![]() and $(M_{q})_{q\in \mathcal {Q}}\in \prod _{q\in \mathcal {Q}}{_{A}\mathsf {Mod}}$
and $(M_{q})_{q\in \mathcal {Q}}\in \prod _{q\in \mathcal {Q}}{_{A}\mathsf {Mod}}$![]() there are isomorphisms
there are isomorphisms

where the second isomorphism holds by 1.8. On the other hand, one has

where the second isomorphism holds again by 1.8. Thus, $(i^{*},\,i_{*},\,i^{!})$![]() is an adjoint triple.
is an adjoint triple.
We mention that the Serre functor $\mathbb {S}$![]() induces an equivalence
induces an equivalence
with $\mathbb {S}_{*}(X)(q)=X(\mathbb {S}(q))$![]() and $\mathbb {S}_{*}^{-1}(X)(q)=X(\mathbb {S}^{-1}(q))$
and $\mathbb {S}_{*}^{-1}(X)(q)=X(\mathbb {S}^{-1}(q))$![]() for each $X\in {_{\mathcal {Q},\,A}\mathsf {Mod}}$
for each $X\in {_{\mathcal {Q},\,A}\mathsf {Mod}}$![]() and $q\in \mathcal {Q}$
and $q\in \mathcal {Q}$![]() . Thus, for each $r\in \mathcal {Q}$
. Thus, for each $r\in \mathcal {Q}$![]() , one has
, one has

where the first and third isomorphisms hold by the definition of Serre functors, the second isomorphism holds as $\mathcal {Q}(r,\,\mathbb {S}(q))$![]() is a finitely generated and projective $\mathbb {k}$
is a finitely generated and projective $\mathbb {k}$![]() -module, and the second equation follows from the fact that $\mathcal {Q}$
-module, and the second equation follows from the fact that $\mathcal {Q}$![]() satisfies the local boundedness. Thus, one has $i^{*}\cong \mathbb {S}_{*}^{-1}\circ i^{!}$
satisfies the local boundedness. Thus, one has $i^{*}\cong \mathbb {S}_{*}^{-1}\circ i^{!}$![]() by the naturality of the above isomorphisms, and so $i^{!}\cong \mathbb {S}_{*}\circ i^{*}.$
by the naturality of the above isomorphisms, and so $i^{!}\cong \mathbb {S}_{*}\circ i^{*}.$![]() Since $(i^{*},\,i_{*})$
Since $(i^{*},\,i_{*})$![]() is an adjoint pair, it is easy to check that $(i^{!},\, i_{*}\circ \mathbb {S}_{*}^{-1})$
is an adjoint pair, it is easy to check that $(i^{!},\, i_{*}\circ \mathbb {S}_{*}^{-1})$![]() is an adjoint pair. This yields that $(i_{*},\, i^{!})$
is an adjoint pair. This yields that $(i_{*},\, i^{!})$![]() is a Frobenius pair of type $(\mathbb {S}_{*}^{-1},\, \mathrm {id}_{\prod _{q\in \mathcal {Q}}{_{A}\mathsf {Mod}}})$
is a Frobenius pair of type $(\mathbb {S}_{*}^{-1},\, \mathrm {id}_{\prod _{q\in \mathcal {Q}}{_{A}\mathsf {Mod}}})$![]() .
.
Theorem 3.6 An object $X\in {_{\mathcal {Q},\,A}\mathsf {Mod}}$![]() is Gorenstein projective if and only if each left $A$
is Gorenstein projective if and only if each left $A$![]() -module $X(q)$
-module $X(q)$![]() is Gorenstein projective for $q\in \mathcal {Q}$
is Gorenstein projective for $q\in \mathcal {Q}$![]() .
.
Proof. It follows from lemma 3.5 that $i_{*}$![]() is a Frobenius functor, and it is faithful clearly. Thus, the desired conclusion holds by lemma 3.3.
is a Frobenius functor, and it is faithful clearly. Thus, the desired conclusion holds by lemma 3.3.
Dually, we have the following result for Gorenstein injective objects.
Theorem 3.7 An object $X\in {_{\mathcal {Q},\,A}\mathsf {Mod}}$![]() is Gorenstein injective if and only if each left $A$
is Gorenstein injective if and only if each left $A$![]() -module $X(q)$
-module $X(q)$![]() is Gorenstein injective for $q\in \mathcal {Q}$
is Gorenstein injective for $q\in \mathcal {Q}$![]() .
.
In the following we give a characterization for Gorenstein flat object in ${_{\mathcal {Q},\,A}\mathsf {Mod}}$![]() . We mention that by [Reference Holm and Jørgensen14, Corollary 3.9] there is an adjoint triple $(F'_{q},\,E'_{q},\,G'_{q})$
. We mention that by [Reference Holm and Jørgensen14, Corollary 3.9] there is an adjoint triple $(F'_{q},\,E'_{q},\,G'_{q})$![]() for each $q\in \mathcal {Q}$
for each $q\in \mathcal {Q}$![]() as follows (see 1.8):
as follows (see 1.8):

Lemma 3.8 For each $M\in {_{A}\mathsf {Mod}}$![]() , $N\in \mathsf {Mod}_{A}$
, $N\in \mathsf {Mod}_{A}$![]() and $E\in {_{\mathbb {k}}\mathsf {Mod}}$
and $E\in {_{\mathbb {k}}\mathsf {Mod}}$![]() , there are isomorphisms
, there are isomorphisms
and
Proof. We only prove the first isomorphism; the second one is proved similarly.
For each $p\in \mathcal {Q}$![]() , one has
, one has

where the second isomorphism holds as $\mathbb {S}$![]() is a Serre functor, and the third one holds since the $\mathbb {k}$
is a Serre functor, and the third one holds since the $\mathbb {k}$![]() -module $\mathcal {Q}(p,\,\mathbb {S}(q))$
-module $\mathcal {Q}(p,\,\mathbb {S}(q))$![]() is finitely generated and projective. It follows that $G'_{q}(\operatorname {Hom}_{\mathbb {k}}\left (M,E\right ))\cong \operatorname {Hom}_{\mathbb {k}}\left (G_{\mathbb {S}(q)}(M),E\right )$
is finitely generated and projective. It follows that $G'_{q}(\operatorname {Hom}_{\mathbb {k}}\left (M,E\right ))\cong \operatorname {Hom}_{\mathbb {k}}\left (G_{\mathbb {S}(q)}(M),E\right )$![]() by the naturality of the above isomorphisms.
by the naturality of the above isomorphisms.
Lemma 3.9 For each $N\in \mathsf {Mod}_{A}$![]() and $X\in {_{\mathcal {Q},\,A}\mathsf {Mod}}$
and $X\in {_{\mathcal {Q},\,A}\mathsf {Mod}}$![]() , there is an isomorphism
, there is an isomorphism
Proof. For each $E\in {_{\mathbb {k}}\mathsf {Mod}}$![]() , there are isomorphisms
, there are isomorphisms

where the first isomorphism follows from (1.6.1), the second one holds by lemma 3.8, and the third one holds as $(E_{\mathbb {S}(q)},\,G_{\mathbb {S}(q)})$![]() is an adjoint pair; see 1.8. Thus, there is an isomorphism $G'_{q}(N)\otimes _{Q,A}X\cong N\otimes _{A}X(\mathbb {S}(q))$
is an adjoint pair; see 1.8. Thus, there is an isomorphism $G'_{q}(N)\otimes _{Q,A}X\cong N\otimes _{A}X(\mathbb {S}(q))$![]() .
.
Lemma 3.10 Let $X$![]() be an object in ${_{\mathcal {Q},\,A}\mathsf {Mod}}$
be an object in ${_{\mathcal {Q},\,A}\mathsf {Mod}}$![]() such that each left $A$
such that each left $A$![]() -module $X(q)$
-module $X(q)$![]() is Gorenstein flat for $q\in \mathcal {Q}$
is Gorenstein flat for $q\in \mathcal {Q}$![]() . Then $\operatorname {Tor}_{\mathcal {Q},\,A}^{i}\left (E,X\right )=0$
. Then $\operatorname {Tor}_{\mathcal {Q},\,A}^{i}\left (E,X\right )=0$![]() for each injective object $E$
for each injective object $E$![]() in $\mathsf {Mod}_{\mathcal {Q},\,A}$
in $\mathsf {Mod}_{\mathcal {Q},\,A}$![]() and all $i\geq 1$
and all $i\geq 1$![]() .
.
Proof. Fix an injective object $E$![]() in $\mathsf {Mod}_{\mathcal {Q},\,A}$
in $\mathsf {Mod}_{\mathcal {Q},\,A}$![]() . Let $I$
. Let $I$![]() be a faithful injective right $A$
be a faithful injective right $A$![]() -module. Then for all $q\in \mathcal {Q}$
-module. Then for all $q\in \mathcal {Q}$![]() the objects $G'_{q}(I)$
the objects $G'_{q}(I)$![]() are injective and cogenerate $\mathsf {Mod}_{\mathcal {Q},\,A}$
are injective and cogenerate $\mathsf {Mod}_{\mathcal {Q},\,A}$![]() ; see [Reference Holm and Jørgensen14, Proposition 3.12]. Thus, $E$
; see [Reference Holm and Jørgensen14, Proposition 3.12]. Thus, $E$![]() is a direct summand of an object of the form $\prod _{q\in \mathcal {Q}}\ G'_{q}(I).$
is a direct summand of an object of the form $\prod _{q\in \mathcal {Q}}\ G'_{q}(I).$![]() We mention that $\prod _{q\in \mathcal {Q}}\ G'_{q}(I) \cong \coprod _{q\in \mathcal {Q}} G'_{q}(I)$
We mention that $\prod _{q\in \mathcal {Q}}\ G'_{q}(I) \cong \coprod _{q\in \mathcal {Q}} G'_{q}(I)$![]() by [Reference Holm and Jørgensen15, Proposition 3.7]. Since the functor $\operatorname {Tor}_{\mathcal {Q},\,A}^{i}\left (-,X\right )$
by [Reference Holm and Jørgensen15, Proposition 3.7]. Since the functor $\operatorname {Tor}_{\mathcal {Q},\,A}^{i}\left (-,X\right )$![]() converts coproducts to coproducts, without loss of generality we may assume that $E$
converts coproducts to coproducts, without loss of generality we may assume that $E$![]() has the form $G'_{q}(I)$
has the form $G'_{q}(I)$![]() . Let $\mathbf {P}$
. Let $\mathbf {P}$![]() be a projective resolution of $X$
be a projective resolution of $X$![]() . Then for each $i\geq 1$
. Then for each $i\geq 1$![]() one has
one has

where the second isomorphism holds by lemma 3.9 and the equality holds as $X(\mathbb {S}(q))$![]() is Gorenstein flat. This completes the proof.
is Gorenstein flat. This completes the proof.
Theorem 3.11 An object $X\in {_{\mathcal {Q},\,A}\mathsf {Mod}}$![]() is Gorenstein flat if and only if each left $A$
is Gorenstein flat if and only if each left $A$![]() -module $X(q)$
-module $X(q)$![]() is Gorenstein flat for $q\in \mathcal {Q}.$
is Gorenstein flat for $q\in \mathcal {Q}.$![]()
Proof. For the ‘only if’ part, let $X$![]() be a Gorenstein flat object in ${_{\mathcal {Q},\,A}\mathsf {Mod}}$
be a Gorenstein flat object in ${_{\mathcal {Q},\,A}\mathsf {Mod}}$![]() . Then there is an exact sequence
. Then there is an exact sequence
of flat objects in ${_{\mathcal {Q},\,A}\mathsf {Mod}}$![]() such that $X\cong \operatorname{Coker} (F_{1}\to F_{0})$
such that $X\cong \operatorname{Coker} (F_{1}\to F_{0})$![]() and the sequence remains exact after applying the functor $E\otimes _{\mathcal {Q},A}-$
and the sequence remains exact after applying the functor $E\otimes _{\mathcal {Q},A}-$![]() for each injective object $E$
for each injective object $E$![]() in $\mathsf {Mod}_{\mathcal {Q},\,A}$
in $\mathsf {Mod}_{\mathcal {Q},\,A}$![]() . Let $I$
. Let $I$![]() be an injective right $A$
be an injective right $A$![]() -module. Then it follows from lemma 3.9 that there is an isomorphism $I\otimes _{A}\mathbf {F}(q)\cong G'_{\mathbb {S}^{-1}(q)}(I)\otimes _{\mathcal {Q},A}\mathbf {F}$
-module. Then it follows from lemma 3.9 that there is an isomorphism $I\otimes _{A}\mathbf {F}(q)\cong G'_{\mathbb {S}^{-1}(q)}(I)\otimes _{\mathcal {Q},A}\mathbf {F}$![]() for each $q\in \mathcal {Q}$
for each $q\in \mathcal {Q}$![]() . We mention that $G'_{\mathbb {S}^{-1}(q)}(I)$
. We mention that $G'_{\mathbb {S}^{-1}(q)}(I)$![]() is an injective object in $\mathsf {Mod}_{\mathcal {Q},\,A}$
is an injective object in $\mathsf {Mod}_{\mathcal {Q},\,A}$![]() . Then the $\mathbb {k}$
. Then the $\mathbb {k}$![]() -complex $G'_{\mathbb {S}^{-1}(q)}(I)\otimes _{\mathcal {Q},A}\mathbf {F}$
-complex $G'_{\mathbb {S}^{-1}(q)}(I)\otimes _{\mathcal {Q},A}\mathbf {F}$![]() is exact, and so $I\otimes _{A}\mathbf {F}(q)$
is exact, and so $I\otimes _{A}\mathbf {F}(q)$![]() is exact. On the other hand, $\mathbf {F}(q)$
is exact. On the other hand, $\mathbf {F}(q)$![]() is an exact sequence of flat left $A$
is an exact sequence of flat left $A$![]() -modules by proposition 1.10, which yields that $X(q)$
-modules by proposition 1.10, which yields that $X(q)$![]() is Gorenstein flat for each $q\in \mathcal {Q}$
is Gorenstein flat for each $q\in \mathcal {Q}$![]() .
.
For the ‘if’ part, let $X$![]() be an object in ${_{\mathcal {Q},\,A}\mathsf {Mod}}$
be an object in ${_{\mathcal {Q},\,A}\mathsf {Mod}}$![]() such that each left $A$
such that each left $A$![]() -module $X(q)$
-module $X(q)$![]() is Gorenstein flat for $q\in \mathcal {Q}$
is Gorenstein flat for $q\in \mathcal {Q}$![]() . Then $i_{*}(X)=(X(q))_{q\in \mathcal {Q}}$
. Then $i_{*}(X)=(X(q))_{q\in \mathcal {Q}}$![]() is a Gorenstein flat object in the product category $\prod _{q\in \mathcal {Q}}{}_{A}\mspace {-1mu}\operatorname {Mod}$
is a Gorenstein flat object in the product category $\prod _{q\in \mathcal {Q}}{}_{A}\mspace {-1mu}\operatorname {Mod}$![]() . Thus, there is an exact sequence
. Thus, there is an exact sequence
in $\prod _{q\in \mathcal {Q}}{}_{A}\mspace {-1mu}\operatorname {Mod}$![]() with $F$
with $F$![]() flat and $Y$
flat and $Y$![]() Gorenstein flat. Denote by $\eta$
Gorenstein flat. Denote by $\eta$![]() and $\varepsilon$
and $\varepsilon$![]() the unit and counit of the adjoint pair $(i_{*},\,i^{!})$
the unit and counit of the adjoint pair $(i_{*},\,i^{!})$![]() , respectively. Set $f=i^{!}(f')\circ \eta _{X}:X\to i^{!}(F)$
, respectively. Set $f=i^{!}(f')\circ \eta _{X}:X\to i^{!}(F)$![]() . Since $i_{*}$
. Since $i_{*}$![]() is faithful and $i^{!}$
is faithful and $i^{!}$![]() is exact, it follows that $f$
is exact, it follows that $f$![]() is a monomorphism. Consequently, one gets an exact sequence
is a monomorphism. Consequently, one gets an exact sequence
in ${}_{\mathcal {Q},\,A}\mspace {-1mu}\operatorname {Mod}$![]() . Since $f'=\varepsilon _{F}\circ i_{*}(f)$
. Since $f'=\varepsilon _{F}\circ i_{*}(f)$![]() , there is a pull-back diagram
, there is a pull-back diagram

which yields an exact sequence
We mention that $i_{*}$![]() and $i^{!}$
and $i^{!}$![]() preserve flats as $(i_{*},\, i^{!})$
preserve flats as $(i_{*},\, i^{!})$![]() is a Frobenius pair by lemma 3.5. Then it follows from [Reference Šaroch and Št'ovíček22, Corollary 4.12] that $i_{*}(X')$
is a Frobenius pair by lemma 3.5. Then it follows from [Reference Šaroch and Št'ovíček22, Corollary 4.12] that $i_{*}(X')$![]() is a Gorenstein flat object in the product category $\prod _{q\in \mathcal {Q}}{}_{A}\mspace {-1mu}\operatorname {Mod}$
is a Gorenstein flat object in the product category $\prod _{q\in \mathcal {Q}}{}_{A}\mspace {-1mu}\operatorname {Mod}$![]() . Thus, for each injective object $E$
. Thus, for each injective object $E$![]() in $\mathsf {Mod}_{\mathcal {Q},\,A}$
in $\mathsf {Mod}_{\mathcal {Q},\,A}$![]() one has $\operatorname {Tor}_{\mathcal {Q},\,A}^{i}\left (E,X'\right )=0$
one has $\operatorname {Tor}_{\mathcal {Q},\,A}^{i}\left (E,X'\right )=0$![]() for all $i\geq 1$
for all $i\geq 1$![]() by lemma 3.10. Set $F_{0}=i^{!}(F)$
by lemma 3.10. Set $F_{0}=i^{!}(F)$![]() and repeat the above argument for $X'$
and repeat the above argument for $X'$![]() . One obtains inductively an exact sequence
. One obtains inductively an exact sequence
in ${}_{\mathcal {Q},\,A}\mspace {-1mu}\operatorname {Mod}$![]() with each $F_{i}$
with each $F_{i}$![]() flat such that it remains exact after applying the functor $E\otimes _{\mathcal {Q},A}-$
flat such that it remains exact after applying the functor $E\otimes _{\mathcal {Q},A}-$![]() for every injective object $E$
for every injective object $E$![]() in $\mathsf {Mod}_{\mathcal {Q},\,A}$
in $\mathsf {Mod}_{\mathcal {Q},\,A}$![]() . Thus, it follows from lemma 3.10 that $X$
. Thus, it follows from lemma 3.10 that $X$![]() is an Gorenstein flat object in ${}_{\mathcal {Q},\,A}\mspace {-1mu}\operatorname {Mod}$
is an Gorenstein flat object in ${}_{\mathcal {Q},\,A}\mspace {-1mu}\operatorname {Mod}$![]() .
.
We end this section with the following result for projectively coresolved Gorenstein flat objects, which can be proved similarly as in theorem 3.11.
Theorem 3.12 An object $X\in {_{\mathcal {Q},\,A}\mathsf {Mod}}$![]() is projectively coresolved Gorenstein flat if and only if each left $A$
is projectively coresolved Gorenstein flat if and only if each left $A$![]() -module $X(q)$
-module $X(q)$![]() is projectively coresolved Gorenstein flat for $q\in \mathcal {Q}.$
is projectively coresolved Gorenstein flat for $q\in \mathcal {Q}.$![]()
Acknowledgements
We thank Henrik Holm and Peter Jørgensen for valuable comments on a draft of this paper. Thanks are also due to the anonymous referee for helpful suggestions that improved the exposition.
Z.X. Di was partly supported by NSF of China (grant No. 11971388), the Scientific Research Funds of Huaqiao University (grant No. 605-50Y22050) and the Fujian Alliance of Mathematics (grant No. 2024SXLMMS04); L.P. Li was partly supported by NSF of China (grant No. 12171146); L. Liang was partly supported by NSF of China (grant No. 12271230) and the Foundation for Innovative Fundamental Research Group Project of Gansu Province (grant No. 23JRRA684); Y. Ma was partly supported by NSF of Gansu Province (grant No. 23JRRA866) and the Youth Foundation of Lanzhou Jiaotong University (grant No. 2023023).