No CrossRef data available.
Article contents
Functions with small BMO norm
Published online by Cambridge University Press: 08 January 2025
Abstract
We characterize the functions with ‘small’ bounded mean oscillation (BMO) norm by establishing the precise connection between the space BMO and class 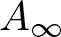 $A_\infty$ of Muckenhoupt weights. We prove that there exists a universal constant
$A_\infty$ of Muckenhoupt weights. We prove that there exists a universal constant  $c^*_2$ such that
$c^*_2$ such that  $\Vert f \Vert_{BMO} \lt c^*_2$ if and only if
$\Vert f \Vert_{BMO} \lt c^*_2$ if and only if  $\exp f \in A_2$, where
$\exp f \in A_2$, where 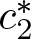 $c^*_2$ is the sharp constant in the John and Nirenberg inequality. Similarly, in dimension one, we prove that
$c^*_2$ is the sharp constant in the John and Nirenberg inequality. Similarly, in dimension one, we prove that  $\Vert f \Vert_{BLO} \lt 1$ if and only if
$\Vert f \Vert_{BLO} \lt 1$ if and only if  $\exp f \in A_1$. As application we introduce a structure of metric space in
$\exp f \in A_1$. As application we introduce a structure of metric space in  $A_\infty$ and prove that the closed unit ball of
$A_\infty$ and prove that the closed unit ball of  $A_\infty$ is a Banach space.
$A_\infty$ is a Banach space.
Keywords
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh



