Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-14T06:24:01.125Z Has data issue: false hasContentIssue false
  • English
  • Français

Infinitely many arbitrarily small positive solutions for the Dirichlet problem involving the p-Laplacian

Published online by Cambridge University Press:  12 July 2007

Giovanni Anello  and
Giuseppe Cordaro
Giovanni Anello
Affiliation:
Department of Mathematics, University of Messina, 98166 Sant' Agata-Messina, Italy (anello@dipmat.unime.it)
Giuseppe Cordaro
Affiliation:
Department of Mathematics, University of Messina, 98166 Sant' Agata-Messina, Italy (cordaro@dipmat.unime.it)
Get access Rights & Permissions [Opens in a new window]

Abstract

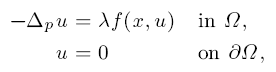In this paper we present a result of existence of infinitely many arbitrarily small positive solutions to the following Dirichlet problem involving the p-Laplacian, where Ω ∈ RN is a bounded open set with sufficiently smooth boundary ∂Ω, p > 1, λ > 0, and f: Ω × R → R is a Carathéodory function satisfying the following condition: there exists t̄ > 0 such that 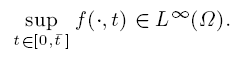Precisely, our result ensures the existence of a sequence of a.e. positive weak solutions to the above problem, converging to zero in L∞(Ω).

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 132 , Issue 3 , June 2002 , pp. 511 - 519
Copyright
Copyright © Royal Society of Edinburgh 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)