Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gomes, Gracinda M. S.
and
Howie, John M.
1987.
Nilpotents in finite symmetric inverse semigroups.
Proceedings of the Edinburgh Mathematical Society,
Vol. 30,
Issue. 3,
p.
383.
Sullivan, R. P.
1994.
Products of nilpotent linear transformations.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 124,
Issue. 6,
p.
1135.
Lima, Lucinda M.
1994.
Nilpotent local automorphisms of an independence algebra.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 124,
Issue. 3,
p.
423.
Xiuliang, Yang
1998.
On the nilpotent ranks of the principal factors of certain semigroups of partial transformations.
Communications in Algebra,
Vol. 26,
Issue. 5,
p.
1445.
Marques-Smith, M. Paula O.
and
Sullivan, R.P.
1999.
The ideal structure of nilpotent-generated transformation semigroups.
Bulletin of the Australian Mathematical Society,
Vol. 60,
Issue. 2,
p.
303.
Mendes-Gonçalves, Suzana
and
Sullivan, R. P.
2005.
Inverse semigroups generated by linear transformations.
Bulletin of the Australian Mathematical Society,
Vol. 71,
Issue. 2,
p.
205.
Marques-Smith, M. Paula O.
and
Sullivan, R.P.
2006.
Congruences on semigroups generated by injective nilpotent transformations.
Bulletin of the Australian Mathematical Society,
Vol. 74,
Issue. 3,
p.
393.
Gomes, Gracinda M. S.
and
Ruškuc, Nik
2014.
John Macintosh Howie: work and legacy.
Semigroup Forum,
Vol. 89,
Issue. 1,
p.
2.
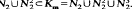
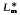 of Lm also has these properties and is congruence-free.
of Lm also has these properties and is congruence-free.