Using the method of generalized characteristics, we discuss the regularity and large time behaviour of admissible weak solutions of a single conservation law, in one space variable, with one inflection point.
We show that when the initial data are C∞ then, generically, the solution is C∞ except: (a) on a finite set of C∞ arcs across which it experiences jump discontinuities (genuine shocks or left contact discontinuities); (b) on a finite set of straight line characteristic segments across which its derivatives of order m, m = 1, 2,…, experience jump discontinuities (weak waves of order m); and (c) on the finite set of points of interaction of shocks and weak waves. Weak waves of order 1 are triggered by rays grazing upon contact discontinuities. Weak waves of order m, m ≥ 2, are generated by the collision of a weak wave of order m − 1 with a left contact discontinuity.
We establish sharp decay rates for solutions with initial data of the following types: (a) with bounded primitive; (b) with primitive having sublinear growth; (c) in L1; (d) of compact support; and (e) periodic.
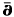 in certain weakly pseudoconvex domains of ℂ2
in certain weakly pseudoconvex domains of ℂ2