Hostname: page-component-66644f4456-mv4w6 Total loading time: 0 Render date: 2025-02-12T20:20:00.818Z Has data issue: true hasContentIssue false
  • English
  • Français

Isotypical components of the homology of ICIS and images of deformations of map germs

Part of: Theory of singularities and catastrophe theory

Published online by Cambridge University Press:  11 February 2025

R. Giménez Conejero Open the ORCID record for R. Giménez Conejero [Opens in a new window]
R. Giménez Conejero*
Affiliation:
Department of Mathematics, Mid Sweden University, Sidsjövägen 2, 852 33 Sundsvall, Sweden (gicoro@uv.es)
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

We give a simple way to study the isotypical components of the homology of simplicial complexes with actions of finite groups and use it for Milnor fibres of isolated complete intersection singularity (icis). We study the homology of images of mappings ft that arise as deformations of complex map germs 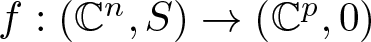$f:(\mathbb{C}^n,S)\to(\mathbb{C}^p,0)$, with n < p, and the behaviour of singularities (instabilities) in this context. We study two generalizations of the notion of image Milnor number µI given by Mond and give a workable way of compute them, in corank one, with Milnor numbers of icis. We also study two unexpected traits when 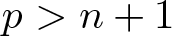$p \gt n+1$: stable perturbations with contractible image and homology of 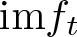$\text{im} f_t$ in unexpected dimensions. We show that Houston’s conjecture, µI constant in a family implies excellency in Gaffney’s sense, is false, but we give a correct modification of the statement of the conjecture which we also prove.

Keywords

coalescencedeformations of map germsexcellent unfoldingshomologyisotypical components

MSC classification

Primary: 58K15: Topological properties of mappings
Secondary: 58K40: Classification; finite determinacy of map germs 58K65: Topological invariants
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 40
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cisneros-Molina, J. L. and Mond, D.. Multiple points of a simplicial map and image-computing spectral sequences. J. Singul. 24 (2022), 190–212.Google Scholar
Cooper, T., Mond, D. and Wik Atique, R.. Vanishing topology of codimension 1 multi-germs over $\mathbb{R}$ and $\mathbb{C}$. Compos. Math. 131 (2002), 121–160.CrossRefGoogle Scholar
de Jong, T. and van Straten, D.. Disentanglements, Singularity Theory and Its Applications, Part I (Coventry, 1988/1989), Lecture Notes in Mathematics, Vol. 1462 (Springer, Berlin, 1991), .Google Scholar
Fernández de Bobadilla, J., Nuño Ballesteros, J. J. and Peñafort Sanchis, G.. A Jacobian module for disentanglements and applications to Mond’s conjecture. Rev. Mat. Complut. 32 (2019), 395–418.CrossRefGoogle Scholar
Gaffney, T.. Polar multiplicities and equisingularity of map germs. Topology. Int. J. Math. 32 (1993), 185–223.Google Scholar
Giménez Conejero, R.. Singularities of germs and vanishing homology. PhD Thesis (Universitat de València, 2021).Google Scholar
Giménez Conejero, R. and Nuño-Ballesteros, J. J.. The image Milnor number and excellent unfoldings. Q. J. Math. 73 (2022), 45–63.CrossRefGoogle Scholar
Giménez Conejero, R., and Nuño-Ballesteros, J. J.. Singularities of mappings on ICIS and applications to Whitney equisingularity. Adv. Math. 408 (2022), 108660, doi:10.1016/j.aim.2022.108660.CrossRefGoogle Scholar
Giménez Conejero, R., and Nuño-Ballesteros, J. J.. A weak version of the Mond conjecture. Collect. Math. (2023), 753–770, doi:10.1007/s13348-023-00411-x.Google Scholar
Goryunov, V. and Mond, D.. Vanishing cohomology of singularities of mappings. Compos. Math. 89 (1993), 45–80.Google Scholar
Goryunov, V. V.. Semi-simplicial resolutions and homology of images and discriminants of mappings. Proc. Lond. Math. Soc. 3rd Series 70(2) (1995), 363–385.CrossRefGoogle Scholar
Greuel, G.-M.. Dualität in der lokalen Kohomologie isolierter Singularitäten. Math. Ann. 250 (1980), 157–173.CrossRefGoogle Scholar
Greuel, G.-M.. Deformation and smoothing of singularities. arXiv:1903.03661 (2019), Mar.1–60.Google Scholar
Greuel, G. M.. Der Gauss-Manin-Zusammenhang isolierter Singularitäten von vollständigen Durchschnitten. Math. Ann. 214 (1975), 235–266.CrossRefGoogle Scholar
Hatcher, A.. Algebraic Topology (Cambridge University Press, Cambridge, 2002).Google Scholar
Houston, K.. Local topology of images of finite complex analytic maps. Topology. Int. J. Math. 36 (1997), 1077–1121.Google Scholar
Houston, K.. On singularities of folding maps and augmentations. Math. Scand. 82 (1998), 191–206.CrossRefGoogle Scholar
Houston, K.. A general image computing spectral sequence, Singularity Theory (World Sci. Publ., Hackensack, NJ, 2007), .Google Scholar
Houston, K.. Stratification of unfoldings of corank 1 singularities. Q. J. Math. 61 (2010), 413–435.CrossRefGoogle Scholar
Houston, K. and Kirk, N.. On the classification and geometry of corank 1 map-germs from three-space to four-space, Singularity Theory (Liverpool, 1996), London Math. Soc. Lecture Note Ser., Vol. 263 (Cambridge University Press, Cambridge, 1999), .Google Scholar
Looijenga, E. and Steenbrink, J.. Milnor number and Tjurina number of complete intersections. Math. Ann. 271 (1985), 121–124.CrossRefGoogle Scholar
Marar, W. L.. The Euler characteristic of the disentanglement of the image of a corank 1 map germ, Lecture Notes in Mathematics, Vol. 1462 (Springer, Berlin, 1991), .Google Scholar
Marar, W. L. and Mond, D.. Multiple point schemes for corank 1 maps. J. Lond. Math. Soc. 2nd Series 39 (1989), 553–567.CrossRefGoogle Scholar
Mond, D.. Some remarks on the geometry and classification of germs of maps from surfaces to 3-space. Topology 26 (1987), 361–383.CrossRefGoogle Scholar
Mond, D.. Vanishing cycles for analytic maps, Singularity Theory and Its Applications, Part I (Coventry, 1988/1989), Lecture Notes in Mathematics, Vol. 1462 (Springer, Berlin, 1991), .CrossRefGoogle Scholar
Mond, D.. Looking at bent wires— ${\mathscr A}_e$-codimension and the vanishing topology of parametrized curve singularities. Math. Proc. Cambridge Philos. Soc. 117 (1995), 213–222.CrossRefGoogle Scholar
Mond, D. and Nuño-Ballesteros, J. J.. Singularities of mappings, Grundlehren der Mathematischen Wissenschaften, Vol. 357 (Springer, Cham, 2020).Google Scholar
Nuño Ballesteros, J. J., Oréfice-Okamoto, B. and Tomazella, J. N.. The vanishing Euler characteristic of an isolated determinantal singularity. Israel J. Math. 197 (2013), 475–495.CrossRefGoogle Scholar
Nuño-Ballesteros, J. J., Oréfice-Okamoto, B. and Tomazella, J. N.. Equisingularity of families of isolated determinantal singularities. Math. Z. 289(3–4) (2018), 1409–1425.CrossRefGoogle Scholar
Sharland, A. A. n.. Examples of finitely determined map-germs of corank 2 from n-space to $(n+1)$-space. Int. J. Math. 25(5) (2014), .CrossRefGoogle Scholar
Sharland, A.. Examples of finitely determined map-germs of corank 3 supporting Mond’s $\mu\geq\tau$-type conjecture. Exp. Math. 28(3) (2019), 257–262.CrossRefGoogle Scholar
Siersma, D.. Vanishing cycles and special fibres, Singularity Theory and Its Applications, Part I (Coventry, 1988/1989), Lecture Notes in Mathematics, Vol. 1462 (Springer, Berlin, 1991), .Google Scholar
W. Inc. Mathematica. Version 12.2 (Champaign, IL, 2020) https://www.wolfram.com/mathematica.Google Scholar
Wall, C. T. C.. A note on symmetry of singularities. Bull. Lond. Math. Soc. 12 (1980), 169–175.CrossRefGoogle Scholar