Large-time behaviour of solutions of Burgers' equation

Abstract

The large-time asymptotic behaviour of real-valued solutions of the pure initial-value problem for Burgers' equation u_t + uu_xu_xx = 0, is studied. The initial data satisfy u₀(x) ~ nx as |x| , where n R. There are two constants of the motion that affect the large-time behaviour: 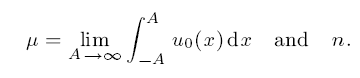Hopf considered the case n = 0 (i.e. u₀L¹(R)), and the case 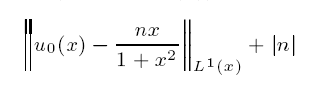sufficiently small was considered by Dix. Here we completely remove that smallness condition. When n < 1, we find an explicit function U(), depending only on and n, such that 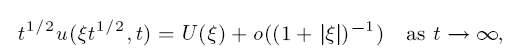uniformly in . When n 1, there are two different functions U() that simultaneously attract the quantity t¹²u(t¹², t), and each one wins in its own range of . Thus we give an asymptotic description of the solution in different regions and compute its decay rate in L. Sharp error estimates are proved.