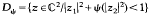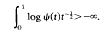Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bonneau, P.
and
Diederich, K.
1990.
Integral solution operators for the Cauchy-Riemann equations on pseudoconvex domains.
Mathematische Annalen,
Vol. 286,
Issue. 1-3,
p.
77.
Adachi, Kenzō
and
Cho, Hong Rae
1997.
Lp (1 ≤ p ≤ ∞) estimates for on a certain pseudoconvex domain in ℂn.
Nagoya Mathematical Journal,
Vol. 148,
Issue. ,
p.
127.
Adachi, Kenzo
1999.
Recent Developments in Complex Analysis and Computer Algebra.
Vol. 4,
Issue. ,
p.
1.
AHN, Heungju
and
CHO, Hong Rae
2002.
Zero sets of holomorphic functions in the Nevanlinna type class on convex domains in C<sup>2</sup>.
Japanese journal of mathematics. New series,
Vol. 28,
Issue. 2,
p.
245.
Ha, Ly Kim
2017.
Zero varieties for the Nevanlinna class in weakly pseudoconvex domains of maximal type F in $$\mathbb {C}^2$$ C 2.
Annals of Global Analysis and Geometry,
Vol. 51,
Issue. 4,
p.
327.
Ha, Ly Kim
2017.
Tangential Cauchy–Riemann Equations on Pseudoconvex Boundaries of Finite and Infinite Type in $$\mathbb {C}^2$$ C 2.
Results in Mathematics,
Vol. 72,
Issue. 1-2,
p.
105.
Ha, Ly Kim
and
Khoi, Le Hai
2019.
Composition Operators Between Hardy Spaces on Linearly Convex Domains in
$$\mathbb {C}^2$$
C
2
.
Complex Analysis and Operator Theory,
Vol. 13,
Issue. 6,
p.
2589.
Ha, Ly Kim
2019.
On Hölder Estimates with Loss of Order One for the
∂
̄
$\bar {\partial }$
Equation on a Class of Convex Domains of Infinite Type in
ℂ
3
$\mathbb {C}^{3}$
.
Acta Mathematica Vietnamica,
Vol. 44,
Issue. 2,
p.
519.
Ha, Ly Kim
2019.
The Cauchy Transform and Henkin Operator on Convex Domains of Maximal Type F$F$ in ℂ2$\mathbb {C}^{2}$.
Vietnam Journal of Mathematics,
Vol. 47,
Issue. 2,
p.
209.
Kim Ha, Ly
2019.
Hölder and $$L^p$$ Estimates for the $${\bar{\partial }}$$-equation in a class of convex domains of infinite type in $${\mathbb {C}}^n$$.
Monatshefte für Mathematik,
Vol. 190,
Issue. 3,
p.
517.
Ha, Ly Kim
2020.
Ck-regularity for ∂¯-equations for a class of convex domains of infinite type in C2.
Kyoto Journal of Mathematics,
Vol. 60,
Issue. 2,
Ha, Ly Kim
2021.
$$C^k$$-Estimates for $$\bar{\partial }$$-Equation on Certain Convex Domains of Infinite Type in $$\mathbb {C}^n$$.
The Journal of Geometric Analysis,
Vol. 31,
Issue. 2,
p.
2058.
Ha, L. K.
and
An, T. K.
2021.
$$\boldsymbol{L}^{\boldsymbol{p}}$$ and Hölder Estimates for Cauchy–Riemann Equations on Convex Domain of Finite/Infinite Type with Piecewise Smooth Boundary in $$\boldsymbol{\mathbb{C}}^{\mathbf{2}}$$.
Journal of Contemporary Mathematical Analysis (Armenian Academy of Sciences),
Vol. 56,
Issue. 4,
p.
225.
Kim Ha, Ly
and
Hai Khoi, Le
2024.
Composition operators between Bergman spaces on infinite type convex domains in ℂ
2
.
Complex Variables and Elliptic Equations,
Vol. 69,
Issue. 8,
p.
1392.


 in certain weakly pseudoconvex domains of ℂ
in certain weakly pseudoconvex domains of ℂ