Hostname: page-component-784d4fb959-2gr9v Total loading time: 0 Render date: 2025-07-15T11:06:40.224Z Has data issue: false hasContentIssue false
  • English
  • Français

The moving plane method and the uniqueness of high-order elliptic equation with GJMS operator

Part of: Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  10 July 2025

Shihong Zhang
Shihong Zhang*
Affiliation:
School of Mathematics, Nanjing University, Nanjing, Jiangsu Province, China (dg21210019@smail.nju.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study the following high-order elliptic equation involving the GJMS operator: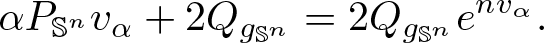

\begin{align*}\alpha P_{\mathbb{S}^n}v_{\alpha}+2Q_{g_{\mathbb{S}^n}}=2Q_{g_{\mathbb{S}^n}}e^{nv_{\alpha}}.\end{align*}

We establish that if α > 1 and 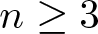$n\geq3$ or if 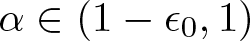$\alpha\in (1-\epsilon_0, 1)$ with 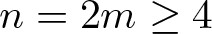$n=2m\geq4$, then 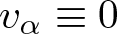$v_{\alpha}\equiv0$. As an application, we present a new proof of the classical Beckner inequality.

Keywords

GJMS operatormoving planeconcentration compactness

MSC classification

Primary: 35A23: Inequalities involving derivatives and differential and integral operators, inequalities for integrals 35J60: Nonlinear elliptic equations
Secondary: 35B33: Critical exponents 35B38: Critical points

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 45
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adimurthi, F. R. and Struwe, M.. Concentration phenomena for Liouville’s equation in dimension four. J. Eur. Math. Soc. (JEMS). 8 (2006), 171–180.Google Scholar
Aubin, T.. Meilleures constantes dans le théorème d’inclusion de Sobolev et un théorème de Fredholm non linéaire pour la transformation conforme de la courbure scalaire. (French) J. Functional Analysis. 32 (1979), 148–174.Google Scholar
Aubin, T.. Nonlinear analysis on manifolds. Monge-Ampère equations. Grundl. JMath. Wiss, Vol.252, (Springer-Verlag, New York, 1982).Google Scholar
Beckner, W.. Sharp Sobolev inequalities on the sphere and the Moser-Trudinger inequality. Ann. of Math. (2). 138 (1993), 213–242.Google Scholar
Branson, T., Chang, S. -Y. A. and Yang, P. C.. Estimates and extremals for zeta function determinants on four-manifolds. Comm. Math. Phys. 149 (1992), 241–262 no.Google Scholar
Brezis, H. and Merle, F.. Uniform estimates and blow-up behavior for solutions of $-\Delta u=V(x)e^u$ in two dimensions. Comm. Partial Differential Equations. 16 (1991), 8–, 1223–1253.Google Scholar
Chang, S. -Y. A. and Yang, P. C.. Prescribing Gaussian curvature on $\mathbb{S}^2$. Acta Math. 159 (1987), 3–, 215–259.Google Scholar
Chang, S. -Y. A. and Yang, P. C.. Extremal metrics of zeta function determinants on 4-manifolds. Ann. of Math. (2). 142 (1995), 171–212.Google Scholar
Chang, S. -Y. A. and Yang, P. C.. On uniqueness of solutions of nth order differential equations in conformal geometry. Math. Res. Lett. 4 (1997), 91–102.Google Scholar
Chanillo, S. and Kiessling, M.. Rotational symmetry of solutions of some nonlinear problems in statistical mechanics and in geometry. Comm. Math. Phys. 160 (1994), 217–238.Google Scholar
Chen, L., Lu, G. and Zhu, M.. Existence and nonexistence of extremals for critical Adams inequalities in $\mathbb{R}^4$ and Trudinger-Moser inequalities in $\mathbb{R}^2$. Adv. Math. 368 (2020), 107143, 61.Google Scholar
Chen, W. and Li, C. Classification of solutions of some nonlinear elliptic equations. Duke Math. J. 63 (1991), 615–622.Google Scholar
Druet, O. and Robert, F.. Bubbling phenomena for fourth-order four-dimensional PDEs with exponential growth. Proc. Amer. Math. Soc. 134 (2006), 897–908.Google Scholar
Feldman, J., Froese, R. and , N. Ghoussoub and C.Gui, An improved Moser-Aubin-Onofri inequality for axially symmetric functions on $\mathbb{S}^2$. Calc. Var. Partial Differential Equations. 6 (1998), 95–104.Google Scholar
Gui, C., Hu, Y. and Xie, W.. Improved Beckner’s inequality for axially symmetric functions on $\mathbb{S}^n$. J. Funct. Anal. 5 (2022), 47.Google Scholar
Gui, C. and Moradifam, A.. The sphere covering inequality and its applications. Invent. Math. 214 (2018), 1169–1204.Google Scholar
Gui, C. and Wei, J.. On a sharp Moser-Aubin-Onofri inequality for functions on $\mathbb{S}^2$ with symmetry. Pacific J. Math. 194 (2000), 349–358.Google Scholar
Hang, F.. A remark on the concentration compactness principle in critical dimension. Comm. Pure Appl. Math. 75 (2022), 10, 2245–2278.Google Scholar
Hang, F.. Aubin type almost sharp Moser-Trudinger inequality revisited. J. Geom. Anal. 9 (2022), 40.Google Scholar
Hyder, A.. Concentration phenomena to a higher order Liouville equation. Calc. Var. Partial Differential Equations. 59 (2020), 4, 126, 23.Google Scholar
Hyder, A., Mancini, G. and Martinazzi, L.. Local and nonlocal singular Liouville equations in Euclidean spaces. Int. Math. Res. Not. IMRN. 15 (2021), 11393–11425.Google Scholar
Jin, T., Li, Y. Y. and Xiong, J.. On a fractional Nirenberg problem, part I: blow up analysis and compactness of solutions. J. Eur. Math. Soc. (JEMS). 16 (2014), 6, 1111–1171.Google Scholar
Li, Y. Y.. Harnack type inequality: the method of moving planes. Comm. Math. Phys. 200 (1999), 421–444.Google Scholar
Lin, C.. Uniqueness of solutions to the mean field equations for the spherical Onsager vortex. Arch. Ration. Mech. Anal. 153 (2000), 153–176.Google Scholar
Lin, C. S.. A classification of solutions of a conformally invariant fourth order equation in $\mathbb{R}^n$. Comment. Math. Helv. 73 (1998), 206–231 no.Google Scholar
Malchiodi, A.. Compactness of solutions to some geometric fourth-order equations. J. Reine Angew. Math. 594 (2006), 137–174.Google Scholar
Martinazzi, L.. Classification of solutions to the higher order Liouville’s equation on $\mathbb{R}^{2m}$. Math. Z., 263, 307–329 (2009)Google Scholar
Martinazzi, L.. Concentration-compactness phenomena in the higher order Liouville’s equation. J. Funct. Anal. 256 (2009), 3743–3771.Google Scholar
Martinazzi, L.. Quantization for the prescribed Q-curvature equation on open domains. Commun. Contemp. Math. 13 (2011), 533–551.Google Scholar
, N. G. and Lin, C.. On the best constant in the Moser-Onofri-Aubin inequality. Comm. Math. Phys. 298 (2010), 869–878.Google Scholar
Ndiaye, C. B.. Constant Q-curvature metrics in arbitrary dimension. J. Funct. Anal. 251 (2007), 1–58.Google Scholar
Ndiaye, C. B.. Algebraic topological methods for the supercritical Q -curvature problem. Adv. Math. 277 (2015), 56–99.Google Scholar
Onofri, E.. On the positivity of the effective action in a theory of random surfaces. Comm. Math. Phys. 86 (1982), 321–326.Google Scholar
Osgood, B., Phillips, R. and Sarnak, P.. Extremals of determinants of Laplacians. J. Funct. Anal. 80 (1988), 148–211.Google Scholar
Wei, J. and , X. Xu Classification of solutions of higher order conformally invariant equations. Math. Ann. 313 (1999), 207–228.Google Scholar
Wei, J. and Xu, X.. On conformal deformations of metrics on $\mathbb{S}^n$. J. Funct. Anal. 157 (1998), 292–325.Google Scholar
Wei, J. and Ye, D.. Nonradial solutions for a conformally invariant fourth order equation in $\mathbb{R}^4$ Calc. Var. Partial Differential Equations. 32 (2008), 373–386.Google Scholar
Xiong, J.. A derivation of the sharp Moser-Trudinger-Onofri inequalities from the fractional Sobolev inequalities. Peking Math. J. 1 (2018), 2, 221–229.Google Scholar
Zhang, S.. A Liouville type theorem of the linearly perturbed Paneitz equation on $\mathbb{S}^3$. Int. Math. Res. Not. IMRN. 2 (2023), 1730–1759.Google Scholar
Zhang, S.. The sharp type Chern-Gauss-Bonnet integral and asymptotic behavior. Adv. Math. 109761 (2024), 36.Google Scholar
Zhang, S.. The non-degenerate condition for prescribed Q curvature problem on $\mathbb{S}^n$. Results Math. 5 (2024), 15.Google Scholar