Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-14T05:14:58.100Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear eigenvalue–eigenvector problems for STP matrices

Published online by Cambridge University Press:  12 July 2007

Uri Elias  and
Allan Pinkus
Uri Elias
Affiliation:
Department of Mathematics, Technion, IIT, Haifa 32000, Israel
Allan Pinkus
Affiliation:
Department of Mathematics, Technion, IIT, Haifa 32000, Israel
Get access Rights & Permissions [Opens in a new window]

Abstract

Let Ai, i = 1, …, m, be a set of Ni × Ni−1 strictly totally positive (STP) matrices, with N0 = Nm = N. For a vector x = (x1, …, xN) ∈ RN and arbitrary p > 0, set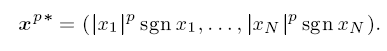 We consider the eigenvalue-eigenvector problem 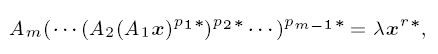where p1 … pm−1 = r. We prove an analogue of the classical Gantmacher-Krein theorem for the eigenvalue-eigenvector structure of STP matrices in the case where pi ≥ 1 for each i, plus various extensions thereof.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 132 , Issue 6 , December 2002 , pp. 1307 - 1331
Copyright
Copyright © Royal Society of Edinburgh 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)