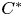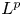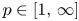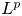1. Introduction
Topological freeness is a key condition in the study of the $C^*$![]() -algebras associated to discrete group actions and their generalizations, see [Reference Archbold and Spielberg4, Reference Exel, Laca and Quigg17, Reference Kawamura and Tomiyama27, Reference Kwaśniewski and Meyer28, Reference Kwaśniewski and Meyer30, Reference Kwaśniewski and Meyer31, Reference O'Donovan33, Reference Olesen and Pedersen34, Reference Tomiyama41, Reference Zeller-Meier43]. It is crucial for the description of the ideal structure and for pure infiniteness criteria of various $C^*$
-algebras associated to discrete group actions and their generalizations, see [Reference Archbold and Spielberg4, Reference Exel, Laca and Quigg17, Reference Kawamura and Tomiyama27, Reference Kwaśniewski and Meyer28, Reference Kwaśniewski and Meyer30, Reference Kwaśniewski and Meyer31, Reference O'Donovan33, Reference Olesen and Pedersen34, Reference Tomiyama41, Reference Zeller-Meier43]. It is crucial for the description of the ideal structure and for pure infiniteness criteria of various $C^*$![]() -algebras, and is known to be closely related to such conditions as pure outerness, proper outerness, full Connes spectrum, aperiodicity, almost extension property, uniqueness of a pseudo-expectation, detection of ideals, supporting, filling, maximal abelian or Cartan inclusions, see [Reference Kwaśniewski and Meyer28, Reference Kwaśniewski and Meyer31] and references therein. Topological freeness is also important in the spectral analysis of weighted composition operators on $L^2$
-algebras, and is known to be closely related to such conditions as pure outerness, proper outerness, full Connes spectrum, aperiodicity, almost extension property, uniqueness of a pseudo-expectation, detection of ideals, supporting, filling, maximal abelian or Cartan inclusions, see [Reference Kwaśniewski and Meyer28, Reference Kwaśniewski and Meyer31] and references therein. Topological freeness is also important in the spectral analysis of weighted composition operators on $L^2$![]() -spaces, see [Reference Antonevich and Lebedev2, Reference Bardadyn and Kwaśniewski5, Reference O'Donovan33]. The title of the present article alludes to the seminal paper [Reference Archbold and Spielberg4], as we generalize the corresponding results to the setting of twisted Banach algebra crossed products.
-spaces, see [Reference Antonevich and Lebedev2, Reference Bardadyn and Kwaśniewski5, Reference O'Donovan33]. The title of the present article alludes to the seminal paper [Reference Archbold and Spielberg4], as we generalize the corresponding results to the setting of twisted Banach algebra crossed products.
In the 2010s, Phillips initiated a programme of generalizing important $C^*$![]() -algebraic constructions and results to Banach algebras represented on $L^p$
-algebraic constructions and results to Banach algebras represented on $L^p$![]() -spaces for $p\in [1,\,\infty )$
-spaces for $p\in [1,\,\infty )$![]() . In recent years, the number of papers in this direction is rapidly growing, see the survey paper [Reference Gardella19] and/or [Reference Chung13, Reference Gardella19, Reference Gardella and Lupini20, Reference Hejazian and Pooya25, Reference Phillips36], [Reference Austad and Ortega3, Reference Bardadyn, Kwaśniewski and Mckee6, Reference Choi, Gardella and Thiel12, Reference Hetland and Ortega26, Reference Wang and Zhu42]. The increasing importance of this field of research is reflected in the growing number of publications in top notch journals, see [Reference Boedihardjo7, Reference Gardella and Lupini20–Reference Gardella and Thiel23, Reference Hetland and Ortega26]. In particular, Banach algebra crossed products [Reference Dirksen, de Jeu and Wortel14], and so also $L^p$
. In recent years, the number of papers in this direction is rapidly growing, see the survey paper [Reference Gardella19] and/or [Reference Chung13, Reference Gardella19, Reference Gardella and Lupini20, Reference Hejazian and Pooya25, Reference Phillips36], [Reference Austad and Ortega3, Reference Bardadyn, Kwaśniewski and Mckee6, Reference Choi, Gardella and Thiel12, Reference Hetland and Ortega26, Reference Wang and Zhu42]. The increasing importance of this field of research is reflected in the growing number of publications in top notch journals, see [Reference Boedihardjo7, Reference Gardella and Lupini20–Reference Gardella and Thiel23, Reference Hetland and Ortega26]. In particular, Banach algebra crossed products [Reference Dirksen, de Jeu and Wortel14], and so also $L^p$![]() -operator algebra crossed products are one of the most fundamental constructions, cf. [Reference Choi, Gardella and Thiel12, Reference Chung13, Reference Gardella19, Reference Hejazian and Pooya25, Reference Phillips36, Reference Wang and Zhu42].
-operator algebra crossed products are one of the most fundamental constructions, cf. [Reference Choi, Gardella and Thiel12, Reference Chung13, Reference Gardella19, Reference Hejazian and Pooya25, Reference Phillips36, Reference Wang and Zhu42].
In this article, we contribute to the development of this modern theory by solving one of the fundamental problems which is a Banach algebra version of the well-known $C^*$![]() -algebraic simplicity criterion. In particular, Phillips [Reference Phillips36, Question 8.2] and Gardella–Lupini [Reference Gardella and Lupini20, Problem 8.2] ask whether topological freeness and minimality of a discrete group action $\varphi : G\to \operatorname {Homeo}(X)$
-algebraic simplicity criterion. In particular, Phillips [Reference Phillips36, Question 8.2] and Gardella–Lupini [Reference Gardella and Lupini20, Problem 8.2] ask whether topological freeness and minimality of a discrete group action $\varphi : G\to \operatorname {Homeo}(X)$![]() , on a locally compact Hausdorff space $X$
, on a locally compact Hausdorff space $X$![]() , are sufficient for simplicity of the associated reduced $L^p$
, are sufficient for simplicity of the associated reduced $L^p$![]() -operator algebra crossed product. For $C^*$
-operator algebra crossed product. For $C^*$![]() -algebras this is a well-known fact that follows from a theorem of Kawamura–Tomiyama [Reference Kawamura and Tomiyama27], generalized by Archbold–Spielberg in [Reference Archbold and Spielberg4], which characterizes topological freeness of a discrete group action in terms of a generalized intersection property for the full crossed product. This implies simplicity of reduced crossed products for minimal actions, and shows that topological freeness is necessary for simplicity of the full crossed product.
-algebras this is a well-known fact that follows from a theorem of Kawamura–Tomiyama [Reference Kawamura and Tomiyama27], generalized by Archbold–Spielberg in [Reference Archbold and Spielberg4], which characterizes topological freeness of a discrete group action in terms of a generalized intersection property for the full crossed product. This implies simplicity of reduced crossed products for minimal actions, and shows that topological freeness is necessary for simplicity of the full crossed product.
In this paper, we generalize the results of Kawamura–Tomiyama and Archbold–Spielberg in two directions. Firstly, we extend it not only to $L^p$![]() -operator algebras, $p\in [1,\,\infty ]$
-operator algebras, $p\in [1,\,\infty ]$![]() , but to a much more general class of Banach algebra crossed products that we introduce in the paper (see theorem 5.9, corollary 5.8). Secondly, we prove a version of it for twisted actions (theorem 5.12), which is inspired by recent $C^*$
, but to a much more general class of Banach algebra crossed products that we introduce in the paper (see theorem 5.9, corollary 5.8). Secondly, we prove a version of it for twisted actions (theorem 5.12), which is inspired by recent $C^*$![]() -algebraic results [Reference Kwaśniewski and Meyer31], characterizing the generalized intersection property for every intermediate $C^*$
-algebraic results [Reference Kwaśniewski and Meyer31], characterizing the generalized intersection property for every intermediate $C^*$![]() -algebra. Our proofs differ from the original $C^*$
-algebra. Our proofs differ from the original $C^*$![]() -algebraic arguments that usually exploit positivity, a concept absent in the Banach algebra setting. One of the main ideas to overcome this is to use not only the canonical expectation but the whole family of ‘expectations’, indexed by elements of the group $G$
-algebraic arguments that usually exploit positivity, a concept absent in the Banach algebra setting. One of the main ideas to overcome this is to use not only the canonical expectation but the whole family of ‘expectations’, indexed by elements of the group $G$![]() , that we refer to as the Fourier decomposition. An important role is also played by the minimality of the supremum norm in the algebra $C_0(X)$
, that we refer to as the Fourier decomposition. An important role is also played by the minimality of the supremum norm in the algebra $C_0(X)$![]() , that $G$
, that $G$![]() acts upon. Another new ingredient is that in order to have an ‘if and only if’ result for twisted actions, we consider crossed products coming from subgroups $H\subseteq G$
acts upon. Another new ingredient is that in order to have an ‘if and only if’ result for twisted actions, we consider crossed products coming from subgroups $H\subseteq G$![]() . Here in the proof we had to develop new techniques. In particular, we use that any second cohomology group for free groups is trivial and that crossed products for a trivial action can be described as section algebras of a bundle of twisted group algebras. One of the main applications (see theorem 6.3) is that for a topologically free action $\alpha$
. Here in the proof we had to develop new techniques. In particular, we use that any second cohomology group for free groups is trivial and that crossed products for a trivial action can be described as section algebras of a bundle of twisted group algebras. One of the main applications (see theorem 6.3) is that for a topologically free action $\alpha$![]() on the algebra $C_0(X)$
on the algebra $C_0(X)$![]() , and any twist $u\in H^2(G,\, C_u(X))$
, and any twist $u\in H^2(G,\, C_u(X))$![]() , a reduced twisted Banach algebra crossed product $F_{\mathcal {R}}(\alpha,\,u)$
, a reduced twisted Banach algebra crossed product $F_{\mathcal {R}}(\alpha,\,u)$![]() is simple if and only if the action is minimal.
is simple if and only if the action is minimal.
A notion of a reduced Banach algebra crossed product that we introduce (in defintion 4.4) generalizes reduced group Banach algebras defined recently by Phillips in [Reference Phillips37], and has reduced twisted $L^p$![]() -operator algebra crossed products as examples. In fact, all of our results apply to a more general class of $L^P$
-operator algebra crossed products as examples. In fact, all of our results apply to a more general class of $L^P$![]() -operator algebra crossed products where $P\subseteq [1,\,\infty ]$
-operator algebra crossed products where $P\subseteq [1,\,\infty ]$![]() is a set of Hölder exponents (definition 4.12). This class includes as special cases different algebras studied by other authors and allows for nice phrasing of our results. We prove that for amenable actions the full and reduced $L^P$
is a set of Hölder exponents (definition 4.12). This class includes as special cases different algebras studied by other authors and allows for nice phrasing of our results. We prove that for amenable actions the full and reduced $L^P$![]() -crossed products coincide (theorem 3.5 and remark 4.13), and thus for amenable actions simplicity of any $L^P$
-crossed products coincide (theorem 3.5 and remark 4.13), and thus for amenable actions simplicity of any $L^P$![]() -crossed product is equivalent to topological freeness and minimality of the action.
-crossed product is equivalent to topological freeness and minimality of the action.
We also introduce residually reduced Banach algebra crossed products (definition 6.7), which for $C^*$![]() -algebras coincide with reduced crossed products for exact actions [Reference Sierakowski40]. The $L^P$
-algebras coincide with reduced crossed products for exact actions [Reference Sierakowski40]. The $L^P$![]() -operator algebra crossed products for $P\subseteq \{1,\,\infty \}$
-operator algebra crossed products for $P\subseteq \{1,\,\infty \}$![]() are always residually reduced. We show that if $F_{\mathcal {R}}(\alpha,\,u)$
are always residually reduced. We show that if $F_{\mathcal {R}}(\alpha,\,u)$![]() is residually reduced and the action is residually topologically free, then the ideal lattice of $F_{\mathcal {R}}(\alpha,\,u)$
is residually reduced and the action is residually topologically free, then the ideal lattice of $F_{\mathcal {R}}(\alpha,\,u)$![]() is canonically isomorphic to the lattice of $G$
is canonically isomorphic to the lattice of $G$![]() -invariant open subsets of $X$
-invariant open subsets of $X$![]() (theorem 6.13). If in addition $X$
(theorem 6.13). If in addition $X$![]() is second countable, this isomorphism induces a homeomorphism from the prime ideal space $\operatorname {Prime}(F_{\mathcal {R}}(\alpha,\,u))$
is second countable, this isomorphism induces a homeomorphism from the prime ideal space $\operatorname {Prime}(F_{\mathcal {R}}(\alpha,\,u))$![]() onto the quasi-orbit space $\mathcal {O}(X)$
onto the quasi-orbit space $\mathcal {O}(X)$![]() of the action (corollary 6.19). This generalizes, and in some cases improves, well-known results from $C^*$
of the action (corollary 6.19). This generalizes, and in some cases improves, well-known results from $C^*$![]() -algebra theory to a much more general Banach algebra framework.
-algebra theory to a much more general Banach algebra framework.
The paper is organized as follows. In § 2, we fix notation and discuss basic facts concerning the Banach algebra $F(\alpha,\,u)=\ell ^{1}(G,\,C_0(X))$![]() associated to a twisted action $(\alpha,\,u)$
associated to a twisted action $(\alpha,\,u)$![]() on $C_0(X)$
on $C_0(X)$![]() . We also introduce full and reduced twisted $L^p$
. We also introduce full and reduced twisted $L^p$![]() -operator algebra crossed products $F^p(\alpha,\,u)$
-operator algebra crossed products $F^p(\alpha,\,u)$![]() and $F^{p}_{\operatorname {r}}(\alpha,\,u)$
and $F^{p}_{\operatorname {r}}(\alpha,\,u)$![]() , $p\in [1,\,\infty ]$
, $p\in [1,\,\infty ]$![]() . Section 3 is devoted to a detailed proof, built on ideas of [Reference Choi, Gardella and Thiel12], that for amenable actions we always have $F^{p}(\alpha,\,u)=F^{p}_{\operatorname {r}}(\alpha,\,u)$
. Section 3 is devoted to a detailed proof, built on ideas of [Reference Choi, Gardella and Thiel12], that for amenable actions we always have $F^{p}(\alpha,\,u)=F^{p}_{\operatorname {r}}(\alpha,\,u)$![]() . In § 4, we introduce reduced Banach algebra crossed products and more general Banach algebra crossed products $F_{\mathcal {R}}(\alpha,\,u)$
. In § 4, we introduce reduced Banach algebra crossed products and more general Banach algebra crossed products $F_{\mathcal {R}}(\alpha,\,u)$![]() that admit the Fourier decomposition. We also introduce algebras $F^{P}(\alpha,\,u)$
that admit the Fourier decomposition. We also introduce algebras $F^{P}(\alpha,\,u)$![]() and $F^{P}_{\operatorname {r}}(\alpha,\,u)$
and $F^{P}_{\operatorname {r}}(\alpha,\,u)$![]() for any set of parameters $P\subseteq [1,\,\infty ]$
for any set of parameters $P\subseteq [1,\,\infty ]$![]() . Section 5 presents the proofs of our main theorems. Finally, in § 6 we show how they can be used to derive simplicity, or more generally how to describe the ideal structure of residually reduced crossed products.
. Section 5 presents the proofs of our main theorems. Finally, in § 6 we show how they can be used to derive simplicity, or more generally how to describe the ideal structure of residually reduced crossed products.
2. Preliminaries
Throughout this paper, we fix an action $\varphi$![]() of a discrete group $G$
of a discrete group $G$![]() on a locally compact Hausdorff space $X$
on a locally compact Hausdorff space $X$![]() . Thus, $\varphi : G\to \operatorname {Homeo}(X)$
. Thus, $\varphi : G\to \operatorname {Homeo}(X)$![]() is a group homomorphism into a group of homeomorphisms. Equivalently, we fix a group action $\alpha :G\to \operatorname {Aut}(C_0(X))$
is a group homomorphism into a group of homeomorphisms. Equivalently, we fix a group action $\alpha :G\to \operatorname {Aut}(C_0(X))$![]() on the commutative $C^*$
on the commutative $C^*$![]() -algebra $C_0(X)$
-algebra $C_0(X)$![]() of continuous functions vanishing at infinity; as then we necessarily have $\alpha _s(a)=a\circ \varphi _{s^{-1}}$
of continuous functions vanishing at infinity; as then we necessarily have $\alpha _s(a)=a\circ \varphi _{s^{-1}}$![]() , $s\in G$
, $s\in G$![]() , for some action $\varphi$
, for some action $\varphi$![]() on $X$
on $X$![]() . This action uniquely extends to the action $\alpha :G\to \operatorname {Aut}(C_b(X))$
. This action uniquely extends to the action $\alpha :G\to \operatorname {Aut}(C_b(X))$![]() on the $C^*$
on the $C^*$![]() -algebra $C_b(X)$
-algebra $C_b(X)$![]() of continuous bounded functions (the multiplier algebra of $C_0(X)$
of continuous bounded functions (the multiplier algebra of $C_0(X)$![]() ), which in turn restricts to an action on the unitary group $C_u(X)=\{ a\in C_b(X): |a(x)|=1 \text { for all }x\in X\}$
), which in turn restricts to an action on the unitary group $C_u(X)=\{ a\in C_b(X): |a(x)|=1 \text { for all }x\in X\}$![]() of $C_b(X)$
of $C_b(X)$![]() . Thus, we may view the abelian group $C_u(X)$
. Thus, we may view the abelian group $C_u(X)$![]() as a $G$
as a $G$![]() -module, that yields a cohomology for $G$
-module, that yields a cohomology for $G$![]() . We recall that the corresponding group of $2$
. We recall that the corresponding group of $2$![]() -cocycles $Z^2(G,\,C_u(X))$
-cocycles $Z^2(G,\,C_u(X))$![]() consists of maps $u: G\times G\to C_u(X)$
consists of maps $u: G\times G\to C_u(X)$![]() satisfying
satisfying
The second cohomology group $H^2(G,\, C_u(X))$![]() is the quotient of $Z^2(G,\,C_u(X))$
is the quotient of $Z^2(G,\,C_u(X))$![]() by the subgroup of $2$
by the subgroup of $2$![]() -cobundaries, which are maps of the form $d^2(\xi )(s,\,t):=\alpha _s(\xi (t))\xi (st)^{-1}\xi (s)$
-cobundaries, which are maps of the form $d^2(\xi )(s,\,t):=\alpha _s(\xi (t))\xi (st)^{-1}\xi (s)$![]() , $s,\,t\in G$
, $s,\,t\in G$![]() , for some map $\xi :G\to C_u(X)$
, for some map $\xi :G\to C_u(X)$![]() . Thus, two cocycles $u,\,v$
. Thus, two cocycles $u,\,v$![]() are equivalent (cohomologous) if $u(s,\,t)\xi (st)=v(s,\,t)\alpha _s(\xi (t))\xi (s)$
are equivalent (cohomologous) if $u(s,\,t)\xi (st)=v(s,\,t)\alpha _s(\xi (t))\xi (s)$![]() for some $\xi : G\to C_u(X)$
for some $\xi : G\to C_u(X)$![]() and all $s,\,t\in G$
and all $s,\,t\in G$![]() . We say that $u$
. We say that $u$![]() is normalized if $u(1,\,1)=1$
is normalized if $u(1,\,1)=1$![]() . Identity (2.1) implies that $u(1,\,t)=u(1,\,1)$
. Identity (2.1) implies that $u(1,\,t)=u(1,\,1)$![]() and $u(t,\,1)=\alpha _t(u(1,\,1))$
and $u(t,\,1)=\alpha _t(u(1,\,1))$![]() for all $t\in G$
for all $t\in G$![]() . Hence, if $u$
. Hence, if $u$![]() is normalized, then $u(t,\,1)=u(1,\,t)=1$
is normalized, then $u(t,\,1)=u(1,\,t)=1$![]() for all $t\in G$
for all $t\in G$![]() . Every cocycle is equivalent to a normalized one because $u \cdot d^2(\xi )$
. Every cocycle is equivalent to a normalized one because $u \cdot d^2(\xi )$![]() is normalized for any $u$
is normalized for any $u$![]() and $\xi$
and $\xi$![]() with $\xi (1)=\overline {u(1,\,1)}$
with $\xi (1)=\overline {u(1,\,1)}$![]() .
.
To any cocycle $u\in Z^2(G,\,C_u(X))$![]() we associate a Banach $*$
we associate a Banach $*$![]() -algebra
-algebra
equipped with multiplication and involution given by
(associativity of the product $*$![]() is equivalent to identity (2.1), and it implies that $^*$
is equivalent to identity (2.1), and it implies that $^*$![]() is an involution), cf. [Reference Zeller-Meier43, 2.4]. Viewing $F(\alpha,\,u)$
is an involution), cf. [Reference Zeller-Meier43, 2.4]. Viewing $F(\alpha,\,u)$![]() as the closed linear span of elements $a_s\delta _s$
as the closed linear span of elements $a_s\delta _s$![]() where $\delta _s$
where $\delta _s$![]() is the indicator of $s\in G$
is the indicator of $s\in G$![]() and $a_s \in C_0(X)$
and $a_s \in C_0(X)$![]() , we get
, we get
for all $s,\,t\in G$![]() , $a_{s},\,a_{t}\in C_0(X)$
, $a_{s},\,a_{t}\in C_0(X)$![]() . In particular, $F(\alpha,\,u)=\overline {\bigoplus _{t\in G} C_0(X) \delta _t}$
. In particular, $F(\alpha,\,u)=\overline {\bigoplus _{t\in G} C_0(X) \delta _t}$![]() is a $G$
is a $G$![]() -graded $*$
-graded $*$![]() -algebra, that is $(C_0(X) \delta _s)\cdot (C_0(X) \delta _t)=C_0(X) \delta _{st}$
-algebra, that is $(C_0(X) \delta _s)\cdot (C_0(X) \delta _t)=C_0(X) \delta _{st}$![]() and $(C_0(X)\delta _t)^*=C_0(X)\delta _{t^{-1}}$
and $(C_0(X)\delta _t)^*=C_0(X)\delta _{t^{-1}}$![]() . Also $C_0(X)\ni a\mapsto a u(1,\,1)^*\delta _1\in C_0(X)\delta _1$
. Also $C_0(X)\ni a\mapsto a u(1,\,1)^*\delta _1\in C_0(X)\delta _1$![]() is an isometric isomorphism of Banach algebras allowing us to identify $C_0(X)$
is an isometric isomorphism of Banach algebras allowing us to identify $C_0(X)$![]() with a subalgebra of $F(\alpha,\,u)$
with a subalgebra of $F(\alpha,\,u)$![]() . Any approximate unit in $C_0(X)$
. Any approximate unit in $C_0(X)$![]() is an approximate unit in $F(\alpha,\,u)$
is an approximate unit in $F(\alpha,\,u)$![]() .
.
Definition 2.1 We call $F(\alpha,\,u)$![]() the universal Banach algebra crossed product for $(\alpha,\,u)$
the universal Banach algebra crossed product for $(\alpha,\,u)$![]() . When $u\equiv 1$
. When $u\equiv 1$![]() we write $F(\alpha ):=F(\alpha,\,1)$
we write $F(\alpha ):=F(\alpha,\,1)$![]() .
.
Up to a natural isomorphism $F(\alpha,\,u)$![]() only depends on the equivalence class of $u$
only depends on the equivalence class of $u$![]() :
:
Proposition 2.2 cf. [Reference Zeller-Meier43, Proposition 2.5]
Cocycles $u,\,v\in Z^2(G,\,C_u(X))$![]() are equivalent if and only if $F(\alpha,\,u)\cong F(\alpha,\,v)$
are equivalent if and only if $F(\alpha,\,u)\cong F(\alpha,\,v)$![]() by an isometric isomorphism that respects the $G$
by an isometric isomorphism that respects the $G$![]() -gradings and it is the identity on $C_0(X)$
-gradings and it is the identity on $C_0(X)$![]() . Any such isomorphism $\psi :F(\alpha,\,u) \to F(\alpha,\,v)$
. Any such isomorphism $\psi :F(\alpha,\,u) \to F(\alpha,\,v)$![]() is $*$
is $*$![]() -preserving and is of the form
-preserving and is of the form
where $\xi :G\to C_u(X)$![]() is such that $u=vd^{2}(\xi )$
is such that $u=vd^{2}(\xi )$![]() . Thus, such isomorphisms are parametrized by $1$
. Thus, such isomorphisms are parametrized by $1$![]() -cocycles $Z^1(G,\,C_u(X)):=\{\omega :G\to C_u(X): \omega (st)=\omega (s)\alpha _s (\omega (t))\text { for }s,\,t \in G\}$
-cocycles $Z^1(G,\,C_u(X)):=\{\omega :G\to C_u(X): \omega (st)=\omega (s)\alpha _s (\omega (t))\text { for }s,\,t \in G\}$![]() .
.
Proof. Clearly, for any function $\xi : G\to C_u(X)$![]() , formula (2.3) defines a surjective $C_0(X)$
, formula (2.3) defines a surjective $C_0(X)$![]() -module isometry $\psi : F(\alpha,\,u)\to F(\alpha,\,v)$
-module isometry $\psi : F(\alpha,\,u)\to F(\alpha,\,v)$![]() that respects the $G$
that respects the $G$![]() -grading. Since
-grading. Since
we see that $\psi$![]() is multiplicative if and only if $u(s,\,t)\xi (st)=v(s,\,t)\alpha _s(\xi (t))\xi (s)$
is multiplicative if and only if $u(s,\,t)\xi (st)=v(s,\,t)\alpha _s(\xi (t))\xi (s)$![]() for all $s,\,t\in G$
for all $s,\,t\in G$![]() . Thus, if $\xi$
. Thus, if $\xi$![]() with $u=vd^{2}(\xi )$
with $u=vd^{2}(\xi )$![]() exists, then $\psi$
exists, then $\psi$![]() given by (2.3) is an isometric isomorphism. It is the identity on $C_0(X)$
given by (2.3) is an isometric isomorphism. It is the identity on $C_0(X)$![]() because for any $a\in C_0(X)$
because for any $a\in C_0(X)$![]() , using that $u(1,\,1)=v(1,\,1)\xi (1)$
, using that $u(1,\,1)=v(1,\,1)\xi (1)$![]() , we get
, we get
Using also that $u(t^{-1},\,t) =v(t^{-1},\,t)\alpha _{t^{-1}}(\xi (t))\xi (1)^{*}\xi (t^{-1})$![]() we get $\psi ((a_t\delta _t)^*)=\psi (a_t\delta _t)^*$
we get $\psi ((a_t\delta _t)^*)=\psi (a_t\delta _t)^*$![]() , for any $a_t\in C_0(X)$
, for any $a_t\in C_0(X)$![]() , $t\in G$
, $t\in G$![]() . Thus, $\psi$
. Thus, $\psi$![]() preserves the involution. Moreover, for any $\xi ': G\to C_u(X)$
preserves the involution. Moreover, for any $\xi ': G\to C_u(X)$![]() we have $u=vd^{2}(\xi ')$
we have $u=vd^{2}(\xi ')$![]() if and only if $d^2(\xi '\xi ^{-1})=1$
if and only if $d^2(\xi '\xi ^{-1})=1$![]() if and only if $\xi '=\xi \omega$
if and only if $\xi '=\xi \omega$![]() where $\omega \in Z^1(G,\,C_u(X))$
where $\omega \in Z^1(G,\,C_u(X))$![]() . Hence, isomorphisms given by (2.3) are parametrized by elements of $Z^1(G,\,C_u(X))$
. Hence, isomorphisms given by (2.3) are parametrized by elements of $Z^1(G,\,C_u(X))$![]() .
.
Let us now assume that $\psi : F(\alpha,\,u) \to F(\alpha,\,v)$![]() is any isometric isomorphism respecting the $G$
is any isometric isomorphism respecting the $G$![]() -gradings and $\psi |_{C_0(X)}=\text {id}_{C_0(X)}$
-gradings and $\psi |_{C_0(X)}=\text {id}_{C_0(X)}$![]() . It suffices to show that $\psi$
. It suffices to show that $\psi$![]() satisfies (2.3) for some $\xi :G\to C_u(X)$
satisfies (2.3) for some $\xi :G\to C_u(X)$![]() . The assumption $\psi |_{C_0(X)}=\text {id}_{C_0(X)}$
. The assumption $\psi |_{C_0(X)}=\text {id}_{C_0(X)}$![]() means that $\psi$
means that $\psi$![]() is a $C_0(X)$
is a $C_0(X)$![]() -bimodule map. For each $t\in G$
-bimodule map. For each $t\in G$![]() , we have a left $C_0(X)$
, we have a left $C_0(X)$![]() -module map $E_t: F(\alpha,\,v) \to C_0(X)$
-module map $E_t: F(\alpha,\,v) \to C_0(X)$![]() given by $E_t(b):=b(t)$
given by $E_t(b):=b(t)$![]() , $b\in F(\alpha,\,v)$
, $b\in F(\alpha,\,v)$![]() . Hence, the formula
. Hence, the formula
defines a left $C_0(X)$![]() -module map on $C_0(X)$
-module map on $C_0(X)$![]() . This means that $\xi (t)$
. This means that $\xi (t)$![]() is multiplier of $C_0(X)$
is multiplier of $C_0(X)$![]() . Hence, we may identify $\xi (t)$
. Hence, we may identify $\xi (t)$![]() with a function in $C_b(X)$
with a function in $C_b(X)$![]() , so that $\xi (t)(a)$
, so that $\xi (t)(a)$![]() becomes $\xi (t) \cdot a$
becomes $\xi (t) \cdot a$![]() . This gives a map $\xi :G\to C_u(X)$
. This gives a map $\xi :G\to C_u(X)$![]() . Since $\psi$
. Since $\psi$![]() preserves the grading, for any $t\in G$
preserves the grading, for any $t\in G$![]() and $a_t\in C_0(X)$
and $a_t\in C_0(X)$![]() we have $\psi (a_t\delta _t)=E_t(\psi (a_t\delta _t))\delta _t= (\xi (t) a_t) \delta _t,\,$
we have $\psi (a_t\delta _t)=E_t(\psi (a_t\delta _t))\delta _t= (\xi (t) a_t) \delta _t,\,$![]() as desired.
as desired.
Remark 2.3 In light of proposition 2.2, twisted crossed products are in essence parameterized by the elements in the second cohomology group $H^2(G,\, C_u(X))$![]() , and thus we may restrict our attention to normalized twists. Accordingly, from now on
, and thus we may restrict our attention to normalized twists. Accordingly, from now on
we assume all cocycles are normalized, that is $u(1,\,1)=1$![]() for all $u\in Z^2(G,\,C_u(X))$
for all $u\in Z^2(G,\,C_u(X))$![]() .
.
This is assumed in most sources that deal with crossed products, see [Reference Zeller-Meier43], [Reference Busby and Smith10], [Reference Packer and Raeburn35]. Then the formulas for involution in $F(\alpha,\,u)$![]() and the embedding of $C_0(X)$
and the embedding of $C_0(X)$![]() into $F(\alpha,\,u)$
into $F(\alpha,\,u)$![]() simplify.
simplify.
For any $u\in Z^2(G,\,C_u(X))$![]() , the space $\ell ^{1}(G,\,C_b(X))$
, the space $\ell ^{1}(G,\,C_b(X))$![]() with operations (2.2) is the crossed product for the extended action $\alpha :G\to \operatorname {Aut}(C_b(X))$
with operations (2.2) is the crossed product for the extended action $\alpha :G\to \operatorname {Aut}(C_b(X))$![]() , which naturally embeds into the multiplier algebra $\operatorname {\mathcal {M}}(F(\alpha,\,u))$
, which naturally embeds into the multiplier algebra $\operatorname {\mathcal {M}}(F(\alpha,\,u))$![]() of the crossed product $F(\alpha,\,u)=\ell ^{1}(G,\,C_0(X))$
of the crossed product $F(\alpha,\,u)=\ell ^{1}(G,\,C_0(X))$![]() . Thus, both $C_u(X)$
. Thus, both $C_u(X)$![]() and $G$
and $G$![]() are naturally subgroups in the group of invertible isometries in $\operatorname {\mathcal {M}}(F(\alpha,\,u))$
are naturally subgroups in the group of invertible isometries in $\operatorname {\mathcal {M}}(F(\alpha,\,u))$![]() , where the $G$
, where the $G$![]() -embedding in question is $g\mapsto 1_X\delta _g$
-embedding in question is $g\mapsto 1_X\delta _g$![]() . The group they generate is isomorphic to $E:= C_u(X)\times G$
. The group they generate is isomorphic to $E:= C_u(X)\times G$![]() , where $(a_{s},\,s)(a_{t},\,t):=(a_{s}\alpha _{s}(a_{t})u(s,\,t),\, st)$
, where $(a_{s},\,s)(a_{t},\,t):=(a_{s}\alpha _{s}(a_{t})u(s,\,t),\, st)$![]() , and the obvious sequence $1\to C_u(X) \to E \to G\to 1$
, and the obvious sequence $1\to C_u(X) \to E \to G\to 1$![]() is exact. Equivalence classes of such group extensions of $G$
is exact. Equivalence classes of such group extensions of $G$![]() by $C_u(X)$
by $C_u(X)$![]() correspond to elements in $H^2(G,\, C_u(X))$
correspond to elements in $H^2(G,\, C_u(X))$![]() . In particular, the class of $u$
. In particular, the class of $u$![]() is trivial if and only if the corresponding exact sequence is split, that is there exists a map $\xi :G\to C_u(X)$
is trivial if and only if the corresponding exact sequence is split, that is there exists a map $\xi :G\to C_u(X)$![]() such that $G\ni t \mapsto (\xi (t),\,t)\in E$
such that $G\ni t \mapsto (\xi (t),\,t)\in E$![]() is a group homomorphism. When $G=\mathbb {F}_n$
is a group homomorphism. When $G=\mathbb {F}_n$![]() is a free group on $n\in \mathbb {N}$
is a free group on $n\in \mathbb {N}$![]() generators, such a homomorphism can always be constructed by universality of $\mathbb {F}_n$
generators, such a homomorphism can always be constructed by universality of $\mathbb {F}_n$![]() .
.
Corollary 2.4 The twisted crossed product can be untwisted, in the sense that $F(\alpha,\,u)\cong F(\alpha )$![]() by an isometric isomorphism that respects $G$
by an isometric isomorphism that respects $G$![]() -gradings and is the identity on $C_0(X)$
-gradings and is the identity on $C_0(X)$![]() if and only if $u$
if and only if $u$![]() vanishes in $H^2(G,\, C_u(X))$
vanishes in $H^2(G,\, C_u(X))$![]() . In particular, if $H^2(G,\, C_u(X))=0$
. In particular, if $H^2(G,\, C_u(X))=0$![]() , which always holds when $G$
, which always holds when $G$![]() is a free group, then all twisted crossed products by $\alpha$
is a free group, then all twisted crossed products by $\alpha$![]() are naturally isomorphic to each other.
are naturally isomorphic to each other.
Remark 2.5 By proposition 2.2, isometric automorphisms of $F(\alpha,\,u)$![]() that are $C_0(X)$
that are $C_0(X)$![]() -bimodule maps respecting the $G$
-bimodule maps respecting the $G$![]() -gradings form a group isomorphic to $Z^1(G,\,C_u(X))$
-gradings form a group isomorphic to $Z^1(G,\,C_u(X))$![]() . A $1$
. A $1$![]() -coboundary is a $1$
-coboundary is a $1$![]() -cocycle $\omega :G\to C_u(X)$
-cocycle $\omega :G\to C_u(X)$![]() given by $\omega (t):= a\alpha _t(a^{-1})$
given by $\omega (t):= a\alpha _t(a^{-1})$![]() , $t\in G$
, $t\in G$![]() , for some $a\in C_u(X)$
, for some $a\in C_u(X)$![]() . Such a cocycle corresponds to the inner automorphism of $F(\alpha,\,u)$
. Such a cocycle corresponds to the inner automorphism of $F(\alpha,\,u)$![]() implemented by $a\in C_u(X)$
implemented by $a\in C_u(X)$![]() . Thus, the first cohomology group $H^1(G,\, C_u(X))$
. Thus, the first cohomology group $H^1(G,\, C_u(X))$![]() can be interpreted as the outer automorphism group of the crossed product $F(\alpha,\,u)$
can be interpreted as the outer automorphism group of the crossed product $F(\alpha,\,u)$![]() viewed as a $G$
viewed as a $G$![]() -graded algebra.
-graded algebra.
Definition 2.6 By a representation of a Banach algebra $B$![]() on a Banach space $E$
on a Banach space $E$![]() we mean a contractive homomorphism $\pi :B\to B(E)$
we mean a contractive homomorphism $\pi :B\to B(E)$![]() into the algebra of bounded operators on $E$
into the algebra of bounded operators on $E$![]() . We will usually assume that $\pi$
. We will usually assume that $\pi$![]() is non-degenerate in the sense that $\overline {\pi (B)E}=E$
is non-degenerate in the sense that $\overline {\pi (B)E}=E$![]() . We denote by $\operatorname {Iso}(E)\subseteq B(E)$
. We denote by $\operatorname {Iso}(E)\subseteq B(E)$![]() the group of invertible isometries on $E$
the group of invertible isometries on $E$![]() .
.
It is well known that if $B$![]() has a contractive approximate unit and $\pi$
has a contractive approximate unit and $\pi$![]() is non-degenerate then $\pi$
is non-degenerate then $\pi$![]() extends uniquely to a (unital) representation $\overline {\pi }:\mathcal {M}(B)\to B(E)$
extends uniquely to a (unital) representation $\overline {\pi }:\mathcal {M}(B)\to B(E)$![]() of the multiplier algebra of $B$
of the multiplier algebra of $B$![]() . Note that $C_0(X)$
. Note that $C_0(X)$![]() has a contractive approximate unit which is also an approximate unit in every crossed product $F(\alpha,\,u)$
has a contractive approximate unit which is also an approximate unit in every crossed product $F(\alpha,\,u)$![]() , $u\in Z^2(G,\,C_u(X))$
, $u\in Z^2(G,\,C_u(X))$![]() . We fix a twisted action $(\alpha,\,u)$
. We fix a twisted action $(\alpha,\,u)$![]() on $C_0(X)$
on $C_0(X)$![]() , and extend some classical results for representations of $F(\alpha,\,u)$
, and extend some classical results for representations of $F(\alpha,\,u)$![]() on Hilbert spaces from [Reference Zeller-Meier43] to representations on Banach spaces.
on Hilbert spaces from [Reference Zeller-Meier43] to representations on Banach spaces.
Definition 2.7 A covariant representation of $(\alpha,\,u)$![]() on a Banach space $E$
on a Banach space $E$![]() is a pair $(\pi,\, v)$
is a pair $(\pi,\, v)$![]() where $\pi :C_0(X)\to B(E)$
where $\pi :C_0(X)\to B(E)$![]() is a non-degenerate representation and $v: G\to \operatorname {Iso}(E)$
is a non-degenerate representation and $v: G\to \operatorname {Iso}(E)$![]() satisfies
satisfies
Lemma 2.8 cf. [Reference Zeller-Meier43, Proposition 2.7, 2.8]
Non-degenerate representations of $F(\alpha,\,u)$![]() are in one-to-one correspondence with covariant representations of $(\alpha,\,u)$
are in one-to-one correspondence with covariant representations of $(\alpha,\,u)$![]() . The representation of $F(\alpha,\,u)$
. The representation of $F(\alpha,\,u)$![]() corresponding to $(\pi,\, v)$
corresponding to $(\pi,\, v)$![]() is given by the formula $\pi \rtimes v(b)=\sum _{t\in G}\pi (b(t))v_t$
is given by the formula $\pi \rtimes v(b)=\sum _{t\in G}\pi (b(t))v_t$![]() .
.
Proof. That $\pi \rtimes v(b):=\sum _{t\in G}\pi (b(t))v_t$![]() defines a non-degenerate representation of $F(\alpha,\,u)$
defines a non-degenerate representation of $F(\alpha,\,u)$![]() , for a covariant representation $(\pi,\, v)$
, for a covariant representation $(\pi,\, v)$![]() , is straightforward. Let $\psi :F(\alpha,\,u)\to B(E)$
, is straightforward. Let $\psi :F(\alpha,\,u)\to B(E)$![]() be any non-degenerate representation. Then $\pi :=\psi |_{C_0(X)}$
be any non-degenerate representation. Then $\pi :=\psi |_{C_0(X)}$![]() is a non-denenerate representation of $C_0(X)$
is a non-denenerate representation of $C_0(X)$![]() . For any $t\in G$
. For any $t\in G$![]() and any contractive approximate unit $(\mu _i)$
and any contractive approximate unit $(\mu _i)$![]() in $C_0(X)$
in $C_0(X)$![]() the strong limit $v_t$
the strong limit $v_t$![]() exists and we write $v_t= \text {s-}\lim _{i}\psi (\mu _i\delta _t)$
exists and we write $v_t= \text {s-}\lim _{i}\psi (\mu _i\delta _t)$![]() . Indeed, by the Cohen–Hewitt factorization theorem, any element in $E$
. Indeed, by the Cohen–Hewitt factorization theorem, any element in $E$![]() has the form $\pi (a)\xi$
has the form $\pi (a)\xi$![]() for some $\xi \in E$
for some $\xi \in E$![]() , $a\in C_0(X)$
, $a\in C_0(X)$![]() , and then $\lim _{i}\psi (\mu _i\delta _t)\pi (a)\xi =\lim _{i}\psi (\mu _i \alpha _t(a)\delta _t)\xi =\pi (\alpha _t(a)\delta _t)\xi$
, and then $\lim _{i}\psi (\mu _i\delta _t)\pi (a)\xi =\lim _{i}\psi (\mu _i \alpha _t(a)\delta _t)\xi =\pi (\alpha _t(a)\delta _t)\xi$![]() . This calculation also implies that $v_t\pi (a)=\pi (\alpha _t(a))v_t$
. This calculation also implies that $v_t\pi (a)=\pi (\alpha _t(a))v_t$![]() and $v_t$
and $v_t$![]() does not depend on the choice of an approximate unit. For $s,\,t\in G$
does not depend on the choice of an approximate unit. For $s,\,t\in G$![]() we get
we get

In particular, $v_{t^{-1}} v_{t}=\overline {\pi }(u(t^{-1},\,t))$![]() is an invertible element. Thus, $v_t$
is an invertible element. Thus, $v_t$![]() is in $\operatorname {Iso}(E)$
is in $\operatorname {Iso}(E)$![]() , as an invertible contraction with a contractive inverse. Hence, $(\pi,\, v)$
, as an invertible contraction with a contractive inverse. Hence, $(\pi,\, v)$![]() is a covariant representation. Clearly, $\psi =\pi \rtimes v$
is a covariant representation. Clearly, $\psi =\pi \rtimes v$![]() and $(\pi,\, v)$
and $(\pi,\, v)$![]() is uniquely determined by this equality.
is uniquely determined by this equality.
Definition 2.9 Following [Reference Dirksen, de Jeu and Wortel14, Reference Phillips36], for any class $\mathcal {R}$![]() of representations of $F(\alpha,\,u)$
of representations of $F(\alpha,\,u)$![]() we denote by $F_{\mathcal {R}}(\alpha,\,u)$
we denote by $F_{\mathcal {R}}(\alpha,\,u)$![]() the Hausdorff completion of $F(\alpha,\,u)$
the Hausdorff completion of $F(\alpha,\,u)$![]() in the seminorm given by
in the seminorm given by
Definition 2.10 We say that a Banach space $E$![]() is an $L^p$
is an $L^p$![]() -space, for $p\in [1,\,\infty ]$
-space, for $p\in [1,\,\infty ]$![]() , if there is an isometric isomorphism $E\cong L^{p}(\mu )$
, if there is an isometric isomorphism $E\cong L^{p}(\mu )$![]() for some Lebesgue space $L^{p}(\mu )$
for some Lebesgue space $L^{p}(\mu )$![]() on some measure space $(\Omega,\,\mathcal {F},\,\mu )$
on some measure space $(\Omega,\,\mathcal {F},\,\mu )$![]() . We say that a Banach algebra $B$
. We say that a Banach algebra $B$![]() is an $L^p$
is an $L^p$![]() -operator algebra if there is an isometric representation $B\to B(E)$
-operator algebra if there is an isometric representation $B\to B(E)$![]() into bounded operators on some $L^p$
into bounded operators on some $L^p$![]() -space $E$
-space $E$![]() . Similarly, we define $C_0$
. Similarly, we define $C_0$![]() -spaces as Banach spaces isometrically isomorphic to $C_0(\Omega )$
-spaces as Banach spaces isometrically isomorphic to $C_0(\Omega )$![]() for some topological space $\Omega$
for some topological space $\Omega$![]() , and $C_0$
, and $C_0$![]() -operator algebras as those that can be embedded into $B(C_0(\Omega ))$
-operator algebras as those that can be embedded into $B(C_0(\Omega ))$![]() .
.
We have natural injective representations of $F(\alpha,\,u)$![]() on $L^p$
on $L^p$![]() -spaces (with counting measures) and $C_0$
-spaces (with counting measures) and $C_0$![]() -spaces (of functions on discrete spaces). Recall that $\varphi$
-spaces (of functions on discrete spaces). Recall that $\varphi$![]() is the action of $G$
is the action of $G$![]() on $X$
on $X$![]() dual to the action $\alpha$
dual to the action $\alpha$![]() of $G$
of $G$![]() on $C_0(X)$
on $C_0(X)$![]() , and $u\in Z^2(G,\,C_u(X))$
, and $u\in Z^2(G,\,C_u(X))$![]() is a fixed (normalized) twist.
is a fixed (normalized) twist.
Lemma 2.11 For each $p\in [1,\,\infty )$![]() the formula, for $\xi \in \ell ^p(X\times G)$
the formula, for $\xi \in \ell ^p(X\times G)$![]() , $b\in F(\alpha,\,u)$
, $b\in F(\alpha,\,u)$![]() ,
,
defines an injective non-degenerate representation $\Lambda _p:F(\alpha,\,u)\to B(\ell ^p(X\times G))$![]() . The same formula defines an injective non-degenerate representation $\Lambda _{\infty }:F(\alpha,\,u)\to B(c_0(X\times G))$
. The same formula defines an injective non-degenerate representation $\Lambda _{\infty }:F(\alpha,\,u)\to B(c_0(X\times G))$![]() .
.
Proof. Routine calculations show that the formulas, for $a\in C_0(X)$![]() , $s,\,t\in G$
, $s,\,t\in G$![]() and $x\in X$
and $x\in X$![]() ,
,
define a covariant representation of $(\alpha,\,u)$![]() on $\ell ^p(X\times G)$
on $\ell ^p(X\times G)$![]() or $c_0(X\times G)$
or $c_0(X\times G)$![]() . For instance,
. For instance,

Clearly, $\Lambda _p=\pi \rtimes v$![]() . To see that $\Lambda _p$
. To see that $\Lambda _p$![]() is injective, let $\{\mathbb {1}_{x,t}\}_{(x,t)\in X\times G}$
is injective, let $\{\mathbb {1}_{x,t}\}_{(x,t)\in X\times G}$![]() be the standard Schauder basis in $\ell ^p(X\times G)$
be the standard Schauder basis in $\ell ^p(X\times G)$![]() , and note that, for $a\in C_0(X)$
, and note that, for $a\in C_0(X)$![]() , we have
, we have
If $\Lambda _p(\sum \limits _{s\in G} a_s\delta _s)=0$![]() , then for all $(x,\,t)\in X\times G$
, then for all $(x,\,t)\in X\times G$![]() we have
we have
Since the elements $\{\mathbb {1}_{\varphi (x),st}\}_{s\in G}$![]() are linearly independent and $u(s,\,t)(\varphi _s(x))$
are linearly independent and $u(s,\,t)(\varphi _s(x))$![]() are non-zero numbers, this implies that $a_s(\varphi _s(x))=0$
are non-zero numbers, this implies that $a_s(\varphi _s(x))=0$![]() for all $s\in G$
for all $s\in G$![]() and $x\in X$
and $x\in X$![]() . Hence, $\sum \limits _{s\in G}a_s\delta _s=0$
. Hence, $\sum \limits _{s\in G}a_s\delta _s=0$![]() .
.
Definition 2.12 For $p\in [1,\,\infty )$![]() we define the (full) $L^p$
we define the (full) $L^p$![]() -operator algebra crossed product $F^{p}(\alpha,\,u)$
-operator algebra crossed product $F^{p}(\alpha,\,u)$![]() to be $F_{\mathcal {R}}(\alpha,\,u)$
to be $F_{\mathcal {R}}(\alpha,\,u)$![]() where $\mathcal {R}$
where $\mathcal {R}$![]() is the class of all non-degenerate representations on $L^p$
is the class of all non-degenerate representations on $L^p$![]() -spaces. Thus, $F^{p}(\alpha,\,u)$
-spaces. Thus, $F^{p}(\alpha,\,u)$![]() is the completion of $F(\alpha,\,u)$
is the completion of $F(\alpha,\,u)$![]() in the norm
in the norm
The reduced $L^p$![]() -operator algebra crossed product is $F^{p}_{\operatorname {r}}(\alpha,\,u):=F_{\{\Lambda _p\}}(\alpha,\,u)$
-operator algebra crossed product is $F^{p}_{\operatorname {r}}(\alpha,\,u):=F_{\{\Lambda _p\}}(\alpha,\,u)$![]() . Thus, we may identify $F^p_{\operatorname {r}}(\alpha,\,u)$
. Thus, we may identify $F^p_{\operatorname {r}}(\alpha,\,u)$![]() with $\overline {\Lambda _p(F(\alpha,\,u))}\subseteq B(\ell ^{p}(X\times G))$
with $\overline {\Lambda _p(F(\alpha,\,u))}\subseteq B(\ell ^{p}(X\times G))$![]() . Similarly, we define $F^{\infty }(\alpha,\,u)$
. Similarly, we define $F^{\infty }(\alpha,\,u)$![]() where $\mathcal {R}$
where $\mathcal {R}$![]() is the class of all non-degenerate representations on $C_0$
is the class of all non-degenerate representations on $C_0$![]() -spaces, and $F^{\infty }_{\operatorname {r}}(\alpha,\,u):=F_{\{\Lambda _{\infty }\}}(\alpha,\,u)$
-spaces, and $F^{\infty }_{\operatorname {r}}(\alpha,\,u):=F_{\{\Lambda _{\infty }\}}(\alpha,\,u)$![]() .
.
Remark 2.13 It follows from the results of [Reference Bardadyn, Kwaśniewski and Mckee6] (using the groupoid model for the above crossed products) that we get the same norms and Banach algebras allowing degenerate representations, and then $F^{\infty }(\alpha,\,u)$![]() is also universal for representations on $L^{\infty }$
is also universal for representations on $L^{\infty }$![]() -spaces. For $p=2$
-spaces. For $p=2$![]() the full and reduced crossed products coincide with the standard $C^*$
the full and reduced crossed products coincide with the standard $C^*$![]() -algebraic crossed products $C^*(\alpha,\,u)$
-algebraic crossed products $C^*(\alpha,\,u)$![]() and $C^*_{\operatorname {r}}(\alpha,\,u)$
and $C^*_{\operatorname {r}}(\alpha,\,u)$![]() . It also follows from [Reference Bardadyn, Kwaśniewski and Mckee6] that for $b\in F(\alpha,\,u)$
. It also follows from [Reference Bardadyn, Kwaśniewski and Mckee6] that for $b\in F(\alpha,\,u)$![]() we have
we have
and if $1/p+1/q=1$![]() , then $\|b\|_{L^p}\leq \|b\|_{L^1}^{{1}/{p}}\|b\|_{L^{\infty }}^{{1}/{q}}$
, then $\|b\|_{L^p}\leq \|b\|_{L^1}^{{1}/{p}}\|b\|_{L^{\infty }}^{{1}/{q}}$![]() and $F^{p} (\alpha,\,u)\stackrel {anti}{\cong }F^{q} (\alpha,\,u)$
and $F^{p} (\alpha,\,u)\stackrel {anti}{\cong }F^{q} (\alpha,\,u)$![]() and $F^{p}_{\operatorname {r}} (\alpha,\,u)\stackrel {anti}{\cong }F^{q}_{\operatorname {r}} (\alpha,\,u)$
and $F^{p}_{\operatorname {r}} (\alpha,\,u)\stackrel {anti}{\cong }F^{q}_{\operatorname {r}} (\alpha,\,u)$![]() where the isometric anti-isomorphisms are induced by the involution in $F(\alpha,\,u)$
where the isometric anti-isomorphisms are induced by the involution in $F(\alpha,\,u)$![]() . Thus, we have the following hierarchy of the introduced crossed products each of which is a completion of $F(\alpha,\,u)$
. Thus, we have the following hierarchy of the introduced crossed products each of which is a completion of $F(\alpha,\,u)$![]() :
:

Here the downward arrows are representations which are identities on $F(\alpha,\,u)$![]() , the algebras in the middle column are Banach $*$
, the algebras in the middle column are Banach $*$![]() -algebras and the horizontal anti-isomorphims are given by the involution in $F(\alpha,\,u)$
-algebras and the horizontal anti-isomorphims are given by the involution in $F(\alpha,\,u)$![]() .
.
We also mention a generalization of the trivial representation of a group that only works in the untwisted case. It plays a crucial role in characterization of the generalized intersection property for untwisted crossed products (see theorem 5.9 below), and indirectly it is also used in the proof of the corresponding theorem for twisted crossed products (theorem 5.12).
Example 2.14 The formulas $\pi (a)\xi (x):=a(x)\xi (x)$![]() and $v_t \xi (x):=\xi (\varphi _{t^{-1}}(x))$
and $v_t \xi (x):=\xi (\varphi _{t^{-1}}(x))$![]() define a covariant representation of $\alpha$
define a covariant representation of $\alpha$![]() on each of the spaces $\ell ^{p}(X)$
on each of the spaces $\ell ^{p}(X)$![]() , $p\in [1,\,\infty )$
, $p\in [1,\,\infty )$![]() , and $c_0(X)$
, and $c_0(X)$![]() . We denote their integrated forms by $\Lambda _{p}^{\operatorname {tr}}:F^p(\alpha )\to B(\ell ^{p}(X))$
. We denote their integrated forms by $\Lambda _{p}^{\operatorname {tr}}:F^p(\alpha )\to B(\ell ^{p}(X))$![]() , $\Lambda _{\infty }^{\operatorname {tr}}:F^p(\alpha )\to B(c_0(X))$
, $\Lambda _{\infty }^{\operatorname {tr}}:F^p(\alpha )\to B(c_0(X))$![]() and call them $C_0(X)$
and call them $C_0(X)$![]() -trivial representations of $F(\alpha )$
-trivial representations of $F(\alpha )$![]() . Explicitly,
. Explicitly,
3. Reduced $L^p$ -crossed products and amenable actions
-crossed products and amenable actions
Definition 2.12 agrees with notions introduced by Phillips in [Reference Phillips36] for untwisted crossed products, which were extended to the non-separable setting in [Reference Choi, Gardella and Thiel12] and [Reference Gardella19]. Reduced crossed products in these sources are defined using induced representations. We explain the equivalence between the two approaches. Let $(\alpha,\,u)$![]() be a twisted action on $C_0(X)$
be a twisted action on $C_0(X)$![]() . For any non-degenerate representation $\pi :C_0(X)\to B(E)$
. For any non-degenerate representation $\pi :C_0(X)\to B(E)$![]() on a Banach space $E$
on a Banach space $E$![]() we have a covariant representation of $(\alpha,\, u)$
we have a covariant representation of $(\alpha,\, u)$![]() on $\ell ^{p}(G,\, E)$
on $\ell ^{p}(G,\, E)$![]() , $p\in [1,\,\infty )$
, $p\in [1,\,\infty )$![]() , given by
, given by
$a\in C_0(X)$![]() , $\xi \in \ell ^{p}(G,\, E)$
, $\xi \in \ell ^{p}(G,\, E)$![]() . We call $\operatorname {Ind}_p(\pi ):=\widetilde {\pi }\rtimes \widetilde {v}: F(\alpha,\,u)\to B(\ell ^{p}(G,\, E))$
. We call $\operatorname {Ind}_p(\pi ):=\widetilde {\pi }\rtimes \widetilde {v}: F(\alpha,\,u)\to B(\ell ^{p}(G,\, E))$![]() the $\ell ^p$
the $\ell ^p$![]() -representation induced by $\pi$
-representation induced by $\pi$![]() . Explicitly, for $b\in F(\alpha,\,u)$
. Explicitly, for $b\in F(\alpha,\,u)$![]() we have
we have
Note that if $m_p:C_0(X)\to B(\ell ^p(X))$![]() is given by multiplication: $m_p(a)\xi (x):=a(x)\xi (x)$
is given by multiplication: $m_p(a)\xi (x):=a(x)\xi (x)$![]() , then the representations $\operatorname {Ind}_p(m_p)$
, then the representations $\operatorname {Ind}_p(m_p)$![]() and $\Lambda _p$
and $\Lambda _p$![]() are equivalent (conjugated by the invertible isometry $U\in B(\ell ^p(G,\,\ell ^{p}(X))$
are equivalent (conjugated by the invertible isometry $U\in B(\ell ^p(G,\,\ell ^{p}(X))$![]() given by $U\xi (t)(x):=\xi (t)(\varphi _t(x))$
given by $U\xi (t)(x):=\xi (t)(\varphi _t(x))$![]() ). Similarly, one may define $\operatorname {Ind}_{\infty }(\pi )=\pi \rtimes v: F(\alpha,\,u)\to B(c_0(G,\, E))$
). Similarly, one may define $\operatorname {Ind}_{\infty }(\pi )=\pi \rtimes v: F(\alpha,\,u)\to B(c_0(G,\, E))$![]() and then $\operatorname {Ind}_{\infty }(m_{\infty })\cong \Lambda _{\infty }$
and then $\operatorname {Ind}_{\infty }(m_{\infty })\cong \Lambda _{\infty }$![]() where $m_{\infty }:C_0(X)\to B(c_0(X))$
where $m_{\infty }:C_0(X)\to B(c_0(X))$![]() is given by $m_{\infty }(a)\xi (x):=a(x)\xi (x)$
is given by $m_{\infty }(a)\xi (x):=a(x)\xi (x)$![]() . We now generalize [Reference Choi, Gardella and Thiel12, Proposition 6.4] where $X$
. We now generalize [Reference Choi, Gardella and Thiel12, Proposition 6.4] where $X$![]() is compact, $p\in [1,\,\infty )\setminus \{2\}$
is compact, $p\in [1,\,\infty )\setminus \{2\}$![]() , and there is no twist.
, and there is no twist.
Proposition 3.1 For any $p\in [1,\,\infty )$![]() and $b\in F(\alpha,\,u)$
and $b\in F(\alpha,\,u)$![]() we have
we have
and $\|\Lambda _{\infty }(b)\|=\max \{\|\operatorname {Ind}_{\infty }(\pi )(b)\|: \pi \text { is a non-degenerate representation on a } C_0\text {-space}\}$![]() .
.
Proof. Let $b\in F(\alpha,\,u)$![]() . Since $\Lambda _p\cong \operatorname {Ind}_p(m_p)$
. Since $\Lambda _p\cong \operatorname {Ind}_p(m_p)$![]() we only need to show that $\|\operatorname {Ind}_p(\pi )(b)\| \leq \|\Lambda _p(b)\|$
we only need to show that $\|\operatorname {Ind}_p(\pi )(b)\| \leq \|\Lambda _p(b)\|$![]() for any non-degenerate $\pi$
for any non-degenerate $\pi$![]() on an $L^p$
on an $L^p$![]() -space or $C_0$
-space or $C_0$![]() -space when $p=\infty$
-space when $p=\infty$![]() . Let us first consider the case when $p=\infty$
. Let us first consider the case when $p=\infty$![]() , and let $\pi :C_0(X)\to B(C_0(\Omega ))$
, and let $\pi :C_0(X)\to B(C_0(\Omega ))$![]() be a non-degenerate representation where $\Omega$
be a non-degenerate representation where $\Omega$![]() is some locally compact Hausdorff space. By [Reference Bardadyn, Kwaśniewski and Mckee6, Theorem 2.16] there is a continuous map $\Phi :\Omega \to X$
is some locally compact Hausdorff space. By [Reference Bardadyn, Kwaśniewski and Mckee6, Theorem 2.16] there is a continuous map $\Phi :\Omega \to X$![]() such that $\pi (a)\xi (y)=a(\Phi (y))\xi (y)$
such that $\pi (a)\xi (y)=a(\Phi (y))\xi (y)$![]() for $\xi \in C_0(\Omega )$
for $\xi \in C_0(\Omega )$![]() , $y\in \Omega$
, $y\in \Omega$![]() and $a\in C_0(X)$
and $a\in C_0(X)$![]() . Using this and (2.4), for $\xi \in C_0(G,\, C_0(\Omega ))$
. Using this and (2.4), for $\xi \in C_0(G,\, C_0(\Omega ))$![]() , we get
, we get

and so $\|\operatorname {Ind}_{\infty }(\pi )(b)\| \leq \|\Lambda _{\infty }(b)\|$![]() . For $p=2$
. For $p=2$![]() the assertion is a well-known fact, see [Reference Zeller-Meier43, Theorem 4.11]. Hence, it suffices to consider the case when $p\in [1,\,\infty )\setminus \{2\}$
the assertion is a well-known fact, see [Reference Zeller-Meier43, Theorem 4.11]. Hence, it suffices to consider the case when $p\in [1,\,\infty )\setminus \{2\}$![]() . Let us first consider a probability Borel measure $\mu$
. Let us first consider a probability Borel measure $\mu$![]() on $X$
on $X$![]() and a representation $m_p^{\mu }:C_0(X)\to B(L^p(\mu ))$
and a representation $m_p^{\mu }:C_0(X)\to B(L^p(\mu ))$![]() given by multiplication $m_p^{\mu }(a)\xi (x):=a(x)\xi (x)$
given by multiplication $m_p^{\mu }(a)\xi (x):=a(x)\xi (x)$![]() , $\xi \in L^p(\mu )$
, $\xi \in L^p(\mu )$![]() . Denote by $\operatorname {Ind}_p(\mu )=\operatorname {Ind}_p(m_p^{\mu })$
. Denote by $\operatorname {Ind}_p(\mu )=\operatorname {Ind}_p(m_p^{\mu })$![]() the corresponding representation of $F(\alpha,\,u)$
the corresponding representation of $F(\alpha,\,u)$![]() . Then $\operatorname {Ind}_p(\delta _x)$
. Then $\operatorname {Ind}_p(\delta _x)$![]() , where $\delta _x$
, where $\delta _x$![]() is the point mass measure at $x\in X$
is the point mass measure at $x\in X$![]() , can be treated as a representation on $\ell ^{p}(G)$
, can be treated as a representation on $\ell ^{p}(G)$![]() . Moreover, $\Lambda _p\cong \operatorname {Ind}_p(m_p)\cong \bigoplus _{x\in X/G} \operatorname {Ind}_p(\delta _x)$
. Moreover, $\Lambda _p\cong \operatorname {Ind}_p(m_p)\cong \bigoplus _{x\in X/G} \operatorname {Ind}_p(\delta _x)$![]() where $X/G$
where $X/G$![]() is the orbit space for the action $\varphi$
is the orbit space for the action $\varphi$![]() . Hence, for any $\xi \in \ell ^{p}(X,\,L^p(\mu ))$
. Hence, for any $\xi \in \ell ^{p}(X,\,L^p(\mu ))$![]() , putting $\xi ^x(t)=\xi (t)(x)$
, putting $\xi ^x(t)=\xi (t)(x)$![]() for $x\in X$
for $x\in X$![]() , we get
, we get

Thus, $\| \operatorname {Ind}_p(\mu )(b)\|\leq \|\Lambda _p(b)\|$![]() . Let now $\pi :C_0(X)\to B(L^{p}(\nu ))$
. Let now $\pi :C_0(X)\to B(L^{p}(\nu ))$![]() be any non-degenerate representation on some measure space $(Y,\,\nu )$
be any non-degenerate representation on some measure space $(Y,\,\nu )$![]() . By passing to the extension of the action $\alpha$
. By passing to the extension of the action $\alpha$![]() and representation $\pi$
and representation $\pi$![]() to the algebra ${\mathbb{C}} 1+C_0(X)\subseteq C_{b}(X)$
to the algebra ${\mathbb{C}} 1+C_0(X)\subseteq C_{b}(X)$![]() we may assume that $X$
we may assume that $X$![]() is compact. For every $\varepsilon >0$
is compact. For every $\varepsilon >0$![]() there is $\xi \in \ell ^{p}(G,\,L^{p}(\nu ))$
there is $\xi \in \ell ^{p}(G,\,L^{p}(\nu ))$![]() such that
such that
Since the set $\{t\in G: \xi (t)\neq 0\}$![]() is countable, it generates a countable subgroup $G'$
is countable, it generates a countable subgroup $G'$![]() of $G$
of $G$![]() . Since $\{s\in G: b(s)\neq 0\}$
. Since $\{s\in G: b(s)\neq 0\}$![]() is countable, the $C^*$
is countable, the $C^*$![]() -subalgebra $A$
-subalgebra $A$![]() of $C(X)$
of $C(X)$![]() generated by $\{\alpha _t(b(s)): s\in G,\,t\in G'\}\cup \{u(s,\,t): s,\,t\in G'\}$
generated by $\{\alpha _t(b(s)): s\in G,\,t\in G'\}\cup \{u(s,\,t): s,\,t\in G'\}$![]() is separable, unital and the twisted action $(\alpha,\,u)$
is separable, unital and the twisted action $(\alpha,\,u)$![]() of $G$
of $G$![]() on $C(X)$
on $C(X)$![]() restricts to a twisted action $(\alpha ',\, u')$
restricts to a twisted action $(\alpha ',\, u')$![]() of $G'$
of $G'$![]() on $A$
on $A$![]() . Write $A\cong C(X')$
. Write $A\cong C(X')$![]() for a compact Hausdorff $X'$
for a compact Hausdorff $X'$![]() , and note that $\pi$
, and note that $\pi$![]() restricts to a unital representation $\pi :C(X')\to B( L^{p}(\nu ))$
restricts to a unital representation $\pi :C(X')\to B( L^{p}(\nu ))$![]() . By the proof of [Reference Phillips36, Proposition 1.25] there is a separable Banach subspace $F\subseteq L^{p}(\nu )$
. By the proof of [Reference Phillips36, Proposition 1.25] there is a separable Banach subspace $F\subseteq L^{p}(\nu )$![]() such that $F$
such that $F$![]() is an $L^p$
is an $L^p$![]() -space, $\pi (C(X'))F\subseteq F$
-space, $\pi (C(X'))F\subseteq F$![]() and $\{\xi (t):t\in G\}\subseteq F$
and $\{\xi (t):t\in G\}\subseteq F$![]() . As $F$
. As $F$![]() is a separable $L^p$
is a separable $L^p$![]() -space, there is a standard Borel probability measure $\nu '$
-space, there is a standard Borel probability measure $\nu '$![]() such that $F\cong L^p(\nu ')$
such that $F\cong L^p(\nu ')$![]() . We identify $F=L^p(\nu ')$
. We identify $F=L^p(\nu ')$![]() . Then $\pi$
. Then $\pi$![]() yields a unital representation $\pi ':C(X')\to B(L^{p}(\nu '))$
yields a unital representation $\pi ':C(X')\to B(L^{p}(\nu '))$![]() . By construction $\xi \in \ell ^{p}(G',\,L^{p}(\nu '))\subseteq \ell ^{p}(G,\,L^{p}(\nu ))$
. By construction $\xi \in \ell ^{p}(G',\,L^{p}(\nu '))\subseteq \ell ^{p}(G,\,L^{p}(\nu ))$![]() , $b\in F(\alpha ',\,u')$
, $b\in F(\alpha ',\,u')$![]() and $\operatorname {Ind}_{p}(\pi )(b)\xi =\operatorname {Ind}_{p}(\pi ')(b)\xi$
and $\operatorname {Ind}_{p}(\pi )(b)\xi =\operatorname {Ind}_{p}(\pi ')(b)\xi$![]() . Let $\mu$
. Let $\mu$![]() be a Borel probability measure on $X'$
be a Borel probability measure on $X'$![]() such that $\mu (a)=\nu '(\pi '(a))$
such that $\mu (a)=\nu '(\pi '(a))$![]() for $a\in C(X')$
for $a\in C(X')$![]() . By (the proof of) [Reference Choi, Gardella and Thiel12, Lemma 6.3] we have $\|\operatorname {Ind}_p(\pi ')(b)\|=\|\operatorname {Ind}_p(\mu )(b)\|$
. By (the proof of) [Reference Choi, Gardella and Thiel12, Lemma 6.3] we have $\|\operatorname {Ind}_p(\pi ')(b)\|=\|\operatorname {Ind}_p(\mu )(b)\|$![]() . Hence
. Hence
where $\Lambda _p':F(\alpha ',\,u')\to \ell ^{p}(G',\,L^{p}(\nu '))$![]() is the regular representation (see the previous step). Since $\|\Lambda _p'(b)\|=\sup _{x'\in X'/G'} \| \operatorname {Ind}_p(\delta _{x'})\|$
is the regular representation (see the previous step). Since $\|\Lambda _p'(b)\|=\sup _{x'\in X'/G'} \| \operatorname {Ind}_p(\delta _{x'})\|$![]() there is $x' \in X'$
there is $x' \in X'$![]() with $\|\Lambda _p'(b)\|-\varepsilon \leq \| \operatorname {Ind}_p(\delta _{x'})(b)\|$
with $\|\Lambda _p'(b)\|-\varepsilon \leq \| \operatorname {Ind}_p(\delta _{x'})(b)\|$![]() . Taking any preimage $x\in X$
. Taking any preimage $x\in X$![]() of $x'$
of $x'$![]() under the quotient map $X\twoheadrightarrow X'$
under the quotient map $X\twoheadrightarrow X'$![]() , one verifies that $\|\operatorname {Ind}_p(\delta _{x'})(b)\|=\|\operatorname {Ind}_p(\delta _{x})(b)\|$
, one verifies that $\|\operatorname {Ind}_p(\delta _{x'})(b)\|=\|\operatorname {Ind}_p(\delta _{x})(b)\|$![]() . Consequently, gathering all the pieces together, we get
. Consequently, gathering all the pieces together, we get
which implies that $\|\operatorname {Ind}_p(\pi )(b)\|\leq \|\Lambda _p(b)\|$![]() .
.
Definition 3.2 For any $p\in [1,\,\infty ]$![]() , the representation from lemma 2.11 extends to a representation $\Lambda _p:F^{p}(\alpha,\,u)\to F^p_{\operatorname {r}}(\alpha,\,u)$
, the representation from lemma 2.11 extends to a representation $\Lambda _p:F^{p}(\alpha,\,u)\to F^p_{\operatorname {r}}(\alpha,\,u)$![]() that we call the regular representation.
that we call the regular representation.
By remark 2.13, $\Lambda _1$![]() and $\Lambda _{\infty }$
and $\Lambda _{\infty }$![]() are identity maps (isometric isomorphisms) but for $p\in (1,\,\infty )$
are identity maps (isometric isomorphisms) but for $p\in (1,\,\infty )$![]() the regular representation $\Lambda _p:F^{p}(\alpha,\,u)\to F^p_{\operatorname {r}}(\alpha,\,u)$
the regular representation $\Lambda _p:F^{p}(\alpha,\,u)\to F^p_{\operatorname {r}}(\alpha,\,u)$![]() is not injective in general. Here we give a detailed proof that all $\Lambda _p$
is not injective in general. Here we give a detailed proof that all $\Lambda _p$![]() 's are isometric for amenable actions. This was stated without a proof for non-twisted actions on compact spaces in [Reference Choi, Gardella and Thiel12, Lemma 7.5].
's are isometric for amenable actions. This was stated without a proof for non-twisted actions on compact spaces in [Reference Choi, Gardella and Thiel12, Lemma 7.5].
Definition 3.3 [Reference Anantharaman-Delaroche1, Proposition 2.2(3)]
An action $\varphi :G\to \operatorname {Homeo}(X)$![]() is amenable if there exists an approximate invariant mean, that is a net $(f_i)_{i\in I}$
is amenable if there exists an approximate invariant mean, that is a net $(f_i)_{i\in I}$![]() of finitely supported non-negative functions $f_i:G\to C_c(X)^+$
of finitely supported non-negative functions $f_i:G\to C_c(X)^+$![]() such that the net $\sum _{t\in G} f_i(t)$
such that the net $\sum _{t\in G} f_i(t)$![]() converges compactly to $1$
converges compactly to $1$![]() and the net $\sum _{t\in G} |\alpha _{s}(f_i(t))- f_{i}(st)|$
and the net $\sum _{t\in G} |\alpha _{s}(f_i(t))- f_{i}(st)|$![]() converges compactly to $0$
converges compactly to $0$![]() , for every $s\in G$
, for every $s\in G$![]() (compact convergence means uniform convergence on compact subsets).
(compact convergence means uniform convergence on compact subsets).
Lemma 3.4 Let $p,\,q\in (1,\,\infty )$![]() with $1/p+1/q=1$
with $1/p+1/q=1$![]() . If the action $\varphi$
. If the action $\varphi$![]() is amenable, then there are nets $(g_i)_{i\in I}$
is amenable, then there are nets $(g_i)_{i\in I}$![]() , $(h_i)_{i\in I} \subseteq C_c(G,\,C_c(X)^+)$
, $(h_i)_{i\in I} \subseteq C_c(G,\,C_c(X)^+)$![]() such that each of the nets $\sum _{t\in G} g_i(t)^p$
such that each of the nets $\sum _{t\in G} g_i(t)^p$![]() , $\sum _{t\in G} h_i(t)^q$
, $\sum _{t\in G} h_i(t)^q$![]() and $\sum _{t\in G} h_{i}(st)\alpha _{s}(g_i(t))$
and $\sum _{t\in G} h_{i}(st)\alpha _{s}(g_i(t))$![]() , $s\in G$
, $s\in G$![]() , converge compactly to $1$
, converge compactly to $1$![]() .
.
Proof. If $(f_i)_{i\in I}$![]() is an approximate invariant mean, then $g_i(t):=f_i(t)^{{1}/{p}}$
is an approximate invariant mean, then $g_i(t):=f_i(t)^{{1}/{p}}$![]() and $h_i(t)=f_i(t)^{{1}/{q}}$
and $h_i(t)=f_i(t)^{{1}/{q}}$![]() are the desired nets. Indeed, using Hölders inequality, and that $|a-b|^p\leq |a^p-b^{p}|$
are the desired nets. Indeed, using Hölders inequality, and that $|a-b|^p\leq |a^p-b^{p}|$![]() for $a,\,b\geq 0$
for $a,\,b\geq 0$![]() , for any $s\in G$
, for any $s\in G$![]() we get
we get

As $\sum _{t\in G} f_{i}(t)$![]() converges compactly to $1$
converges compactly to $1$![]() , the above estimate implies that $\sum _{t\in G} \alpha _{s}(g_i(t))h_{i}(st)$
, the above estimate implies that $\sum _{t\in G} \alpha _{s}(g_i(t))h_{i}(st)$![]() also converges compactly to $1$
also converges compactly to $1$![]() .
.
Theorem 3.5 If the action $\varphi$![]() is amenable, then for any $p\in (1,\,\infty )$
is amenable, then for any $p\in (1,\,\infty )$![]() the regular representation $\Lambda _p:F^{p}(\alpha,\,u)\to F^p_{\operatorname {r}}(\alpha,\,u)$
the regular representation $\Lambda _p:F^{p}(\alpha,\,u)\to F^p_{\operatorname {r}}(\alpha,\,u)$![]() is isometric.
is isometric.
Proof. Let $(\pi,\,v)$![]() be a covariant representation of $(\alpha,\,u)$
be a covariant representation of $(\alpha,\,u)$![]() on some Banach space $E$
on some Banach space $E$![]() and let $(g_i)_{i\in I}$
and let $(g_i)_{i\in I}$![]() , $(h_i)_{i\in I}$
, $(h_i)_{i\in I}$![]() be nets in $C_c(G,\,C_c(X)^+)$
be nets in $C_c(G,\,C_c(X)^+)$![]() as in lemma 3.4. For $\xi \in E$
as in lemma 3.4. For $\xi \in E$![]() , $\eta \in E'$
, $\eta \in E'$![]() we put
we put
Then $\xi _i\in \ell ^{p}(G,\,E)$![]() and $\eta _i\in \ell ^{q}(G,\,E')$
and $\eta _i\in \ell ^{q}(G,\,E')$![]() . Using the pairing establishing the isomorphism $\ell ^{p}(G,\,E)'\cong \ell ^{q}(G,\,E')$
. Using the pairing establishing the isomorphism $\ell ^{p}(G,\,E)'\cong \ell ^{q}(G,\,E')$![]() , for any $a\in C_c(X)$
, for any $a\in C_c(X)$![]() and $s\in G$
and $s\in G$![]() we get
we get

By linearity, for every $b\in C_c(G,\,C_c(X))\subseteq F(\alpha,\,u)$![]() we get $\langle \pi \rtimes v (b) \xi,\,\eta \rangle =\lim _{i} \langle \operatorname {Ind}_p(\pi )(b)\xi _{i},\, \eta _{i}\rangle$
we get $\langle \pi \rtimes v (b) \xi,\,\eta \rangle =\lim _{i} \langle \operatorname {Ind}_p(\pi )(b)\xi _{i},\, \eta _{i}\rangle$![]() . This shows that $\pi \rtimes v (b)\neq 0$
. This shows that $\pi \rtimes v (b)\neq 0$![]() implies $\operatorname {Ind}_p(\pi )(b)\neq 0$
implies $\operatorname {Ind}_p(\pi )(b)\neq 0$![]() for any $b\in F(\alpha,\,u)$
for any $b\in F(\alpha,\,u)$![]() . To get norm estimates we specialize to the case where $E=L^p(\mu )$
. To get norm estimates we specialize to the case where $E=L^p(\mu )$![]() for some measure $\mu$
for some measure $\mu$![]() (then $E'=L^{q}(\mu )$
(then $E'=L^{q}(\mu )$![]() ). Without changing the Banach space we may assume that $\mu$
). Without changing the Banach space we may assume that $\mu$![]() is localizable. $E=L^p(\mu )$
is localizable. $E=L^p(\mu )$![]() for some measure $\mu$
for some measure $\mu$![]() (then $E'=L^{q}(\mu )$
(then $E'=L^{q}(\mu )$![]() ). Without changing the Banach space we may assume that $\mu$
). Without changing the Banach space we may assume that $\mu$![]() is localizable. Also we may assume that $p\neq 2$
is localizable. Also we may assume that $p\neq 2$![]() , as for $p=2$
, as for $p=2$![]() the assertion is well known, see [Reference Anantharaman-Delaroche1, Theorem 5.3]. Then $\pi$
the assertion is well known, see [Reference Anantharaman-Delaroche1, Theorem 5.3]. Then $\pi$![]() is given by multiplication operators, so there is a homomorphism $\pi _0:C_0(X)\to L^{\infty }(\mu )$
is given by multiplication operators, so there is a homomorphism $\pi _0:C_0(X)\to L^{\infty }(\mu )$![]() , such that $\pi (a)\xi =\pi _0(a) \cdot \xi$
, such that $\pi (a)\xi =\pi _0(a) \cdot \xi$![]() , $\xi \in L^p(\mu )$
, $\xi \in L^p(\mu )$![]() , see [Reference Bardadyn, Kwaśniewski and Mckee6, Theorem 2.14]. Using this, and that $\sum _{t\in G} g_i(t)^p$
, see [Reference Bardadyn, Kwaśniewski and Mckee6, Theorem 2.14]. Using this, and that $\sum _{t\in G} g_i(t)^p$![]() converges compactly to $1$
converges compactly to $1$![]() , for any $\xi \in \pi (C_c(X))L^{p}(\mu )$
, for any $\xi \in \pi (C_c(X))L^{p}(\mu )$![]() , we get
, we get

Similarly, for $\eta \in \pi (C_c(X))L^{q}(\mu )$![]() we get $\|\eta _i\|\longrightarrow \|\eta \|$
we get $\|\eta _i\|\longrightarrow \|\eta \|$![]() . Thus, for any $b\in C_c(G,\,C_c(X))\subseteq F(\alpha,\,u)$
. Thus, for any $b\in C_c(G,\,C_c(X))\subseteq F(\alpha,\,u)$![]() we have $|\langle \pi \rtimes v (b) \xi,\,\eta \rangle |=|\lim _{i} \langle \operatorname {Ind}_p(\pi )(b)\xi _{i},\, \eta _{i}\rangle |\leq \| \operatorname {Ind}_p(\pi )(b)\| \|\xi \| \|\eta \|$
we have $|\langle \pi \rtimes v (b) \xi,\,\eta \rangle |=|\lim _{i} \langle \operatorname {Ind}_p(\pi )(b)\xi _{i},\, \eta _{i}\rangle |\leq \| \operatorname {Ind}_p(\pi )(b)\| \|\xi \| \|\eta \|$![]() , which implies $\| \pi \rtimes v (b)\|\leq \|\operatorname {Ind}_p(\pi )(b)\|$
, which implies $\| \pi \rtimes v (b)\|\leq \|\operatorname {Ind}_p(\pi )(b)\|$![]() . Since $(\pi,\, v)$
. Since $(\pi,\, v)$![]() was arbitrary, we obtain $\|b\|_{L^p}\leq \|\Lambda _p(b)\|$
was arbitrary, we obtain $\|b\|_{L^p}\leq \|\Lambda _p(b)\|$![]() by proposition 3.1. Therefore, the full and reduced norms coincide.
by proposition 3.1. Therefore, the full and reduced norms coincide.
4. Fourier decomposition and reduced crossed products
Throughout this section $(\alpha,\,u)$![]() is a fixed twisted action on $C_0(X)$
is a fixed twisted action on $C_0(X)$![]() . For each $t\in G$
. For each $t\in G$![]() , the evaluation map $E_{t}(b):=b(t)$
, the evaluation map $E_{t}(b):=b(t)$![]() defines a contractive linear map $E_{t}:F(\alpha,\,u)\to C_0(X)$
defines a contractive linear map $E_{t}:F(\alpha,\,u)\to C_0(X)$![]() , and $b\in F(\alpha,\,u)$
, and $b\in F(\alpha,\,u)$![]() is determined by the coefficients $\{E_{t}(b)\}_{t\in G}\subseteq C_0(X)$
is determined by the coefficients $\{E_{t}(b)\}_{t\in G}\subseteq C_0(X)$![]() . We formalize this structure in other Banach algebra completions of $F(\alpha,\,u)$
. We formalize this structure in other Banach algebra completions of $F(\alpha,\,u)$![]() as follows.
as follows.
Definition 4.1 Let $\mathcal {R}$![]() be a family of representations that separates the points of $F(\alpha,\,u)$
be a family of representations that separates the points of $F(\alpha,\,u)$![]() . We say that $F_{\mathcal {R}}(\alpha,\,u)$
. We say that $F_{\mathcal {R}}(\alpha,\,u)$![]() is a Banach algebra crossed product for $(\alpha,\,u)$
is a Banach algebra crossed product for $(\alpha,\,u)$![]() or that $F_{\mathcal {R}}(\alpha,\,u)$
or that $F_{\mathcal {R}}(\alpha,\,u)$![]() admits the Fourier decomposition if $E_{1}:F(\alpha,\,u)\to C_0(X)$
admits the Fourier decomposition if $E_{1}:F(\alpha,\,u)\to C_0(X)$![]() extends to a contractive map $E_{1}^{\mathcal {R}}:F_{\mathcal {R}}(\alpha,\,u)\to C_0(X)$
extends to a contractive map $E_{1}^{\mathcal {R}}:F_{\mathcal {R}}(\alpha,\,u)\to C_0(X)$![]() .
.
By an ideal in a Banach algebra we always mean a closed two-sided ideal.
Lemma 4.2 If $F_{\mathcal {R}}(\alpha,\,u)$![]() is a Banach algebra crossed product, then each $E_{t}:F(\alpha,\,u)\to C_0(X)$
is a Banach algebra crossed product, then each $E_{t}:F(\alpha,\,u)\to C_0(X)$![]() extends to a contractive map $E_{t}^{\mathcal {R}}:F_{\mathcal {R}}(\alpha,\,u)\to C_0(X)$
extends to a contractive map $E_{t}^{\mathcal {R}}:F_{\mathcal {R}}(\alpha,\,u)\to C_0(X)$![]() , $t\in G$
, $t\in G$![]() . They are left $C_0(X)$
. They are left $C_0(X)$![]() -module maps and their joint kernel $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$
-module maps and their joint kernel $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$![]() is an ideal in $F_{\mathcal {R}}(\alpha,\,u)$
is an ideal in $F_{\mathcal {R}}(\alpha,\,u)$![]() , which has a zero intersection with $C_0(X)$
, which has a zero intersection with $C_0(X)$![]() .
.
Proof. We may assume that $F_{\mathcal {R}}(\alpha,\,u)\subseteq B(E)$![]() acts in a non-degenerate way on some Banach space $E$
acts in a non-degenerate way on some Banach space $E$![]() (one may take $E=F_{\mathcal {R}}(\alpha,\,u)$
(one may take $E=F_{\mathcal {R}}(\alpha,\,u)$![]() ). By lemma 2.8, the inclusion map disintegrates to a covariant representation $(\text {id}_{C_0(X)},\, v)$
). By lemma 2.8, the inclusion map disintegrates to a covariant representation $(\text {id}_{C_0(X)},\, v)$![]() . In particular, $b=\sum _{t\in G} b(t)v_t$
. In particular, $b=\sum _{t\in G} b(t)v_t$![]() for $b\in F(\alpha,\,u)\subseteq F_{\mathcal {R}}(\alpha,\,u)$
for $b\in F(\alpha,\,u)\subseteq F_{\mathcal {R}}(\alpha,\,u)$![]() . The invertible isometries $v_t$
. The invertible isometries $v_t$![]() , $t\in G$
, $t\in G$![]() , are multipliers of $C_c(G,\,C_0(X))\subseteq F(\alpha,\,u)\subseteq F_{\mathcal {R}}(\alpha,\,u)$
, are multipliers of $C_c(G,\,C_0(X))\subseteq F(\alpha,\,u)\subseteq F_{\mathcal {R}}(\alpha,\,u)$![]() , and so also of $F_{\mathcal {R}}(\alpha,\,u)$
, and so also of $F_{\mathcal {R}}(\alpha,\,u)$![]() . Thus, the formula $E_{t}^{\mathcal {R}}(b):=E_{1}^{\mathcal {R}}(b v_{t}^{-1})$
. Thus, the formula $E_{t}^{\mathcal {R}}(b):=E_{1}^{\mathcal {R}}(b v_{t}^{-1})$![]() yields a well-defined contractive map $E_{t}^{\mathcal {R}}:F_{\mathcal {R}}(\alpha,\,u)\to C_0(X)$
yields a well-defined contractive map $E_{t}^{\mathcal {R}}:F_{\mathcal {R}}(\alpha,\,u)\to C_0(X)$![]() . Simple verification, using that $v_{t}^{-1}=\overline {u(t^{-1},\,t)} v_{t^{-1}}= v_{t^{-1}}\overline {u(t,\,t^{-1})}$
. Simple verification, using that $v_{t}^{-1}=\overline {u(t^{-1},\,t)} v_{t^{-1}}= v_{t^{-1}}\overline {u(t,\,t^{-1})}$![]() , shows that $E_{t}^{\mathcal {R}}$
, shows that $E_{t}^{\mathcal {R}}$![]() extends $E_t$
extends $E_t$![]() and we also have $E_{t}^{\mathcal {R}}(b)=\alpha _t(E_{1}^{\mathcal {R}}(v_{t}^{-1}b))$
and we also have $E_{t}^{\mathcal {R}}(b)=\alpha _t(E_{1}^{\mathcal {R}}(v_{t}^{-1}b))$![]() , $b\in F_{\mathcal {R}}(\alpha,\,u)$
, $b\in F_{\mathcal {R}}(\alpha,\,u)$![]() . Since $E_{1}^{\mathcal {R}}$
. Since $E_{1}^{\mathcal {R}}$![]() is $C_0(X)$
is $C_0(X)$![]() -bimodule map, this readily implies that
-bimodule map, this readily implies that
for all $a\in C_0(X)$![]() , $b\in F_{\mathcal{R}}(\alpha,u)$
, $b\in F_{\mathcal{R}}(\alpha,u)$![]() . Similarly, using that $v_{t}^{-1}v_{s}^{-1}=v_{st}^{-1}\overline {u(s,\,t)}$
. Similarly, using that $v_{t}^{-1}v_{s}^{-1}=v_{st}^{-1}\overline {u(s,\,t)}$![]() for any $s,\,t\in G$
for any $s,\,t\in G$![]() and $b\in F_{\mathcal {R}}(\alpha,\,u)$
and $b\in F_{\mathcal {R}}(\alpha,\,u)$![]() we have
we have
Exploiting these relations we see that $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$![]() is an ideal.
is an ideal.
Remark 4.3 A Banach algebra completion $B$![]() of $F(\alpha,\,u)$
of $F(\alpha,\,u)$![]() is of the form $F_{\mathcal {R}}(\alpha,\,u)$
is of the form $F_{\mathcal {R}}(\alpha,\,u)$![]() if and only if $\|b\|_{B}\leq \sum _{t\in G} \|b(t)\|_{\infty }$
if and only if $\|b\|_{B}\leq \sum _{t\in G} \|b(t)\|_{\infty }$![]() for any $b\in F(\alpha,\,u)$
for any $b\in F(\alpha,\,u)$![]() . If this holds, then
. If this holds, then

If the above holds, then the maps $E_{t}^{B}:B\to C_0(X)$![]() , $t\in G$
, $t\in G$![]() , from lemma 4.2, are compositions of $j_B$
, from lemma 4.2, are compositions of $j_B$![]() and evaluations on $C_0(G,\,C_0(X))$
and evaluations on $C_0(G,\,C_0(X))$![]() . In particular, $\bigcap _{t\in G}\ker (E_t^{B})=\ker j_B$
. In particular, $\bigcap _{t\in G}\ker (E_t^{B})=\ker j_B$![]() . If $G$
. If $G$![]() is finite, then $B=F(\alpha,\,u)$
is finite, then $B=F(\alpha,\,u)$![]() as topological algebras, because for $b\in F(\alpha,\,u)$
as topological algebras, because for $b\in F(\alpha,\,u)$![]() we have $\max _{t\in G}\|b(t)\|_{\infty } \leq \|b\|_{B}\leq \sum _{t\in G} \|b(t)\|_{\infty } \leq |G| \max _{t\in G}\|b(t)\|_{\infty }$
we have $\max _{t\in G}\|b(t)\|_{\infty } \leq \|b\|_{B}\leq \sum _{t\in G} \|b(t)\|_{\infty } \leq |G| \max _{t\in G}\|b(t)\|_{\infty }$![]() , and so the norms are equivalent.
, and so the norms are equivalent.
Definition 4.4 Let $F_{\mathcal {R}}(\alpha,\,u)$![]() be a Banach algebra crossed product. We call the maps $\{E_{t}^{\mathcal {R}}\}_{t\in G}$
be a Banach algebra crossed product. We call the maps $\{E_{t}^{\mathcal {R}}\}_{t\in G}$![]() in lemma 4.2 the Fourier decomposition (FD for short) for $F_{\mathcal {R}}(\alpha,\,u)$
in lemma 4.2 the Fourier decomposition (FD for short) for $F_{\mathcal {R}}(\alpha,\,u)$![]() . We say that $F_{\mathcal {R}}(\alpha,\,u)$
. We say that $F_{\mathcal {R}}(\alpha,\,u)$![]() is a reduced crossed product if $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})=\{0\}$
is a reduced crossed product if $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})=\{0\}$![]() , equivalently every $b\in F_{\mathcal {R}}(\alpha,\,u)$
, equivalently every $b\in F_{\mathcal {R}}(\alpha,\,u)$![]() is uniquely determined by the coefficients $\{E_{t}^{\mathcal {R}}(b)\}_{t\in G}\subseteq C_0(X)$
is uniquely determined by the coefficients $\{E_{t}^{\mathcal {R}}(b)\}_{t\in G}\subseteq C_0(X)$![]() .
.
Remark 4.5 Obviously, $F(\alpha,\,u)$![]() is a reduced crossed product. By remark 4.3, a crossed product $F_{\mathcal {R}}(\alpha,\,u)$
is a reduced crossed product. By remark 4.3, a crossed product $F_{\mathcal {R}}(\alpha,\,u)$![]() is reduced if and only if the inclusion $F(\alpha,\,u)\subseteq C_0(G,\,C_0(X))$
is reduced if and only if the inclusion $F(\alpha,\,u)\subseteq C_0(G,\,C_0(X))$![]() extends to a contractive injective linear map $j_{\mathcal {R}}:F_{\mathcal {R}}(\alpha,\,u)\to C_0(G,\,C_0(X))$
extends to a contractive injective linear map $j_{\mathcal {R}}:F_{\mathcal {R}}(\alpha,\,u)\to C_0(G,\,C_0(X))$![]() , and this is automatic when $G$
, and this is automatic when $G$![]() is finite. Every crossed product $F_{\mathcal {R}}(\alpha,\,u)$
is finite. Every crossed product $F_{\mathcal {R}}(\alpha,\,u)$![]() can be reduced in the sense that the quotient of $F_{\mathcal {R}}(\alpha,\,u)$
can be reduced in the sense that the quotient of $F_{\mathcal {R}}(\alpha,\,u)$![]() by $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$
by $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$![]() is naturally a reduced crossed product.
is naturally a reduced crossed product.
Remark 4.6 When $X=\{x\}$![]() and there is no twist, our definition agrees with the notion of an abstract reduced Banach group algebra that Phillips introduced in [Reference Phillips37, Definition 1.1].
and there is no twist, our definition agrees with the notion of an abstract reduced Banach group algebra that Phillips introduced in [Reference Phillips37, Definition 1.1].
Remark 4.7 Exotic $C^*$![]() -algebra crossed products for $(\alpha,\,u)$
-algebra crossed products for $(\alpha,\,u)$![]() , see [Reference Buss, Echterhoff and Willett11], are exactly those crossed products $F_{\mathcal {R}}(\alpha,\,u)$
, see [Reference Buss, Echterhoff and Willett11], are exactly those crossed products $F_{\mathcal {R}}(\alpha,\,u)$![]() which are $C^*$
which are $C^*$![]() -algebras. Up to an isometric isomorphism there is exactly one reduced crossed product for $(\alpha,\,u)$
-algebras. Up to an isometric isomorphism there is exactly one reduced crossed product for $(\alpha,\,u)$![]() which is a $C^*$
which is a $C^*$![]() -algebra, and this is the standard reduced $C^*$
-algebra, and this is the standard reduced $C^*$![]() -algebra crossed product $C_{\operatorname {r}}^*(\alpha,\,u)$
-algebra crossed product $C_{\operatorname {r}}^*(\alpha,\,u)$![]() .
.
Lemma 4.8 For any $p\in [1,\,\infty ]$![]() , $F^{p}_{\operatorname {r}}(\alpha,\,u)$
, $F^{p}_{\operatorname {r}}(\alpha,\,u)$![]() is a reduced crossed product.
is a reduced crossed product.
Proof. Assume that $p<\infty$![]() . We identify $F^{p}_{\operatorname {r}}(\alpha,\,u)$
. We identify $F^{p}_{\operatorname {r}}(\alpha,\,u)$![]() with $\overline {\Lambda _p(F(\alpha,\,u))}\subseteq B(\ell ^p (X\times G))$
with $\overline {\Lambda _p(F(\alpha,\,u))}\subseteq B(\ell ^p (X\times G))$![]() and use the notation from the proof of lemma 2.11. For each $(x,\,t)\in X\times G$
and use the notation from the proof of lemma 2.11. For each $(x,\,t)\in X\times G$![]() we let $P_{x,t}(\xi ):=\xi (x,\,t) \mathbb {1}_{x,t}$
we let $P_{x,t}(\xi ):=\xi (x,\,t) \mathbb {1}_{x,t}$![]() be a contractive projection in $B(\ell ^p(X\times G))$
be a contractive projection in $B(\ell ^p(X\times G))$![]() onto the one-dimensional space $\mathbb {C} \mathbb {1}_{x,t}$
onto the one-dimensional space $\mathbb {C} \mathbb {1}_{x,t}$![]() . For any $b\in B(\ell ^p(X\times G))$
. For any $b\in B(\ell ^p(X\times G))$![]() the series
the series
is strongly convergent and $\|\mathbb {E}_1(b)\|\leq \|b\|$![]() , as for any $\xi \in \ell ^p(X\times G)$
, as for any $\xi \in \ell ^p(X\times G)$![]() we get
we get
(these sums are in fact countable, as $\xi (x,\,t)\neq 0$![]() only for a countable set of pairs $(x,\,t)$
only for a countable set of pairs $(x,\,t)$![]() ). Also if $b\in F(\alpha,\,u)\subseteq F^{p}_{\operatorname {r}}(\alpha,\,u)\subseteq B(\ell ^p(X\times G))$
). Also if $b\in F(\alpha,\,u)\subseteq F^{p}_{\operatorname {r}}(\alpha,\,u)\subseteq B(\ell ^p(X\times G))$![]() , then clearly $\mathbb {E}_1(b)=E_1(b)=b(1)$
, then clearly $\mathbb {E}_1(b)=E_1(b)=b(1)$![]() . Thus $\mathbb {E}_1$
. Thus $\mathbb {E}_1$![]() is a contractive extension of $E_1$
is a contractive extension of $E_1$![]() . For any $t\in G$
. For any $t\in G$![]() , the formula $\mathbb {E}_t(b):=\mathbb {E}_1(b v_{t}^{-1})$
, the formula $\mathbb {E}_t(b):=\mathbb {E}_1(b v_{t}^{-1})$![]() defines a contractive map $\mathbb {E}_t:F^{p}_{\operatorname {r}}(\alpha,\,u)\to C_0(X)$
defines a contractive map $\mathbb {E}_t:F^{p}_{\operatorname {r}}(\alpha,\,u)\to C_0(X)$![]() that extends $E_t$
that extends $E_t$![]() . Hence $\{\mathbb {E}_t\}_{t\in G}$
. Hence $\{\mathbb {E}_t\}_{t\in G}$![]() is the Fourier decomposition of $F^{p}_{\operatorname {r}}(\alpha,\,u)$
is the Fourier decomposition of $F^{p}_{\operatorname {r}}(\alpha,\,u)$![]() . For any $s,\,t\in G$
. For any $s,\,t\in G$![]() , $x\in X$
, $x\in X$![]() we have
we have
The operators of the form $av_{s}$![]() , $a\in C_0(X)$
, $a\in C_0(X)$![]() , $s\in G$
, $s\in G$![]() , and hence also every $b\in F^{p}_{\operatorname {r}}(\alpha,\,u)$
, and hence also every $b\in F^{p}_{\operatorname {r}}(\alpha,\,u)$![]() , maps $\mathbb {1}_{x,t}$
, maps $\mathbb {1}_{x,t}$![]() to the closed linear span of elements $\mathbb {1}_{\varphi _s(x),st}$
to the closed linear span of elements $\mathbb {1}_{\varphi _s(x),st}$![]() , $s\in G$
, $s\in G$![]() . Therefore, if $b\neq 0$
. Therefore, if $b\neq 0$![]() there are $s,\,t\in G$
there are $s,\,t\in G$![]() and $x\in X$
and $x\in X$![]() such that $P_{\varphi _s(x),st} b \mathbb {1}_{x,t}\neq 0$
such that $P_{\varphi _s(x),st} b \mathbb {1}_{x,t}\neq 0$![]() . By (4.2), the latter is equivalent to $\mathbb {E}_s(b)\mathbb {1}_{\varphi _s(x),st}\neq 0$
. By (4.2), the latter is equivalent to $\mathbb {E}_s(b)\mathbb {1}_{\varphi _s(x),st}\neq 0$![]() . Hence, $b\neq 0$
. Hence, $b\neq 0$![]() implies $\mathbb {E}_{s}(b)\neq 0$
implies $\mathbb {E}_{s}(b)\neq 0$![]() for some $s\in G$
for some $s\in G$![]() . Consequently, $\bigcap _{t\in G}\ker (\mathbb {E}_t)=\{0\}$
. Consequently, $\bigcap _{t\in G}\ker (\mathbb {E}_t)=\{0\}$![]() .
.
For $p=\infty$![]() the proof above works with $\ell ^p(X\times G)$
the proof above works with $\ell ^p(X\times G)$![]() replaced by $c_0(X\times G)$
replaced by $c_0(X\times G)$![]() , but also the assertion follows from the case $p=1$
, but also the assertion follows from the case $p=1$![]() using the anti-isomorphism $F^{\infty }_{\operatorname {r}} (\alpha,\,u)\stackrel {anti}{\cong }F^{1}_{\operatorname {r}} (\alpha,\,u)$
using the anti-isomorphism $F^{\infty }_{\operatorname {r}} (\alpha,\,u)\stackrel {anti}{\cong }F^{1}_{\operatorname {r}} (\alpha,\,u)$![]() .
.
Corollary 4.9 For any $p\in [1,\,\infty ]$![]() , $F^{p}(\alpha,\,u)$
, $F^{p}(\alpha,\,u)$![]() admits the Fourier decomposition $\{E_{p,t}\}_{t\in G}$
admits the Fourier decomposition $\{E_{p,t}\}_{t\in G}$![]() and $\bigcap _{t\in G}\ker (E_{p,t})=\ker \Lambda _p$
and $\bigcap _{t\in G}\ker (E_{p,t})=\ker \Lambda _p$![]() is the kernel of the regular representation.
is the kernel of the regular representation.
Proof. Put $E_{p,t}:=\mathbb {E}_t\circ \Lambda _p$![]() , $t\in G$
, $t\in G$![]() , where $\Lambda _p:F^{p}(\alpha,\,u)\to F^p_{\operatorname {r}}(\alpha,\,u)$
, where $\Lambda _p:F^{p}(\alpha,\,u)\to F^p_{\operatorname {r}}(\alpha,\,u)$![]() is the regular representation and $\{\mathbb {E}_{t}\}_{t\in G}$
is the regular representation and $\{\mathbb {E}_{t}\}_{t\in G}$![]() is the Fourier decomposition of $F^p_{ \operatorname {r}}(\alpha,\,u)$
is the Fourier decomposition of $F^p_{ \operatorname {r}}(\alpha,\,u)$![]() given by lemma 4.8.
given by lemma 4.8.
There are canonical ways of producing (reduced) Banach algebra or $*$![]() -Banach algebra crossed products from other (reduced) Banach algebra crossed products:
-Banach algebra crossed products from other (reduced) Banach algebra crossed products:
Lemma 4.10 Let $\|\cdot \|_{\mathcal {R}}$![]() and $\|\cdot \|_{\mathcal {R}_{i}}$
and $\|\cdot \|_{\mathcal {R}_{i}}$![]() , $i\in I$
, $i\in I$![]() , be norms on $F(\alpha,\,u)$
, be norms on $F(\alpha,\,u)$![]() that define Banach algebra crossed products $F_{\mathcal {R}}(\alpha,\,u)$
that define Banach algebra crossed products $F_{\mathcal {R}}(\alpha,\,u)$![]() and $F_{\mathcal {R}_i}(\alpha,\,u)$
and $F_{\mathcal {R}_i}(\alpha,\,u)$![]() , $i\in I$
, $i\in I$![]() , for $(\alpha,\,u)$
, for $(\alpha,\,u)$![]() . Then the formulas
. Then the formulas
define norms that yield Banach algebra crossed products $F_{\mathcal {R}^*}(\alpha,\,u)$![]() , $F_{\{ \mathcal {R}_i\}_{i\in I}}(\alpha,\,u)$
, $F_{\{ \mathcal {R}_i\}_{i\in I}}(\alpha,\,u)$![]() for $(\alpha,\,u)$
for $(\alpha,\,u)$![]() . In particular, the norm $\|a\|_{\mathcal {R},*}:=\max \{\|a\|_{\mathcal {R}},\,\|a^*\|_{\mathcal {R}}\}$
. In particular, the norm $\|a\|_{\mathcal {R},*}:=\max \{\|a\|_{\mathcal {R}},\,\|a^*\|_{\mathcal {R}}\}$![]() defines a crossed product $F_{\mathcal {R},*}(\alpha,\,u)$
defines a crossed product $F_{\mathcal {R},*}(\alpha,\,u)$![]() which is a $*$
which is a $*$![]() -Banach algebra. Moreover, $F_{\mathcal {R}^*}(\alpha,\,u)$
-Banach algebra. Moreover, $F_{\mathcal {R}^*}(\alpha,\,u)$![]() and $F_{\mathcal {R},*}(\alpha,\,u)$
and $F_{\mathcal {R},*}(\alpha,\,u)$![]() are reduced if $F_{\mathcal {R}}(\alpha,\,u)$
are reduced if $F_{\mathcal {R}}(\alpha,\,u)$![]() is, and $F_{\{ \mathcal {R}_i\}_{i\in I}}(\alpha,\,u)$
is, and $F_{\{ \mathcal {R}_i\}_{i\in I}}(\alpha,\,u)$![]() is reduced if and only if all $F_{\mathcal {R}_i}(\alpha,\,u)$
is reduced if and only if all $F_{\mathcal {R}_i}(\alpha,\,u)$![]() , $i\in I$
, $i\in I$![]() , are reduced.
, are reduced.
Proof. Clearly, $\|\cdot \|_{\mathcal {R}^*}$![]() is a submultiplicative norm with $\|b\|_{\mathcal {R}^*}\leq \sum _{t\in G} \|b(t)\|_{\infty }$
is a submultiplicative norm with $\|b\|_{\mathcal {R}^*}\leq \sum _{t\in G} \|b(t)\|_{\infty }$![]() for $b\in F(\alpha,\,u)$
for $b\in F(\alpha,\,u)$![]() (because $\|\cdot \|_{\mathcal {R}}$
(because $\|\cdot \|_{\mathcal {R}}$![]() has these properties). The involution on $F(\alpha,\,u)$
has these properties). The involution on $F(\alpha,\,u)$![]() extends to an antimultiplicative antilinear isometry $*$
extends to an antimultiplicative antilinear isometry $*$![]() from $F_{\mathcal {R}^*}(\alpha,\,u)$
from $F_{\mathcal {R}^*}(\alpha,\,u)$![]() onto $F_{\mathcal {R}}(\alpha,\,u)$
onto $F_{\mathcal {R}}(\alpha,\,u)$![]() . In particular, if $F_{\mathcal {R}}(\alpha,\,u)$
. In particular, if $F_{\mathcal {R}}(\alpha,\,u)$![]() admits the FD, then so does $F_{\mathcal {R}^*}(\alpha,\,u)$
admits the FD, then so does $F_{\mathcal {R}^*}(\alpha,\,u)$![]() , as then $\|b(1)\|=\|b(1)^*\|\leq \|b^*\|_{\mathcal {R}}= \|b\|_{\mathcal {R}^*},\,$
, as then $\|b(1)\|=\|b(1)^*\|\leq \|b^*\|_{\mathcal {R}}= \|b\|_{\mathcal {R}^*},\,$![]() for all $b\in F(\alpha,\,u)$
for all $b\in F(\alpha,\,u)$![]() . Moreover, if $\{E_{t}^{\mathcal {R}}\}_{t\in G}$
. Moreover, if $\{E_{t}^{\mathcal {R}}\}_{t\in G}$![]() is the FD for $F_{\mathcal {R}}(\alpha,\,u)$
is the FD for $F_{\mathcal {R}}(\alpha,\,u)$![]() and $\{E_{t}^{\mathcal {R}^*}\}_{t\in G}$
and $\{E_{t}^{\mathcal {R}^*}\}_{t\in G}$![]() is the FD for $F_{\mathcal {R}^*}(\alpha,\,u)$
is the FD for $F_{\mathcal {R}^*}(\alpha,\,u)$![]() , then by continuity and the formula for involution on $F(\alpha,\,u)$
, then by continuity and the formula for involution on $F(\alpha,\,u)$![]() we get
we get
This readily implies that $F_{\mathcal {R}^*}(\alpha,\,u)$![]() is reduced if and only if $F_{\mathcal {R}}(\alpha,\,u)$
is reduced if and only if $F_{\mathcal {R}}(\alpha,\,u)$![]() is.
is.
Clearly, $\|\cdot \|_{\{ \mathcal {R}_i\}_{i\in I}}$![]() is a submultiplicative norm with $\|b\|_{\{ \mathcal {R}_i\}_{i\in I}}\leq \sum _{t\in G} \|b(t)\|_{\infty }$
is a submultiplicative norm with $\|b\|_{\{ \mathcal {R}_i\}_{i\in I}}\leq \sum _{t\in G} \|b(t)\|_{\infty }$![]() for $b\in F(\alpha,\,u)$
for $b\in F(\alpha,\,u)$![]() (because each $\|\cdot \|_{\mathcal {R}_{i}}$
(because each $\|\cdot \|_{\mathcal {R}_{i}}$![]() has these properties). If there is at least one $i_0\in I$
has these properties). If there is at least one $i_0\in I$![]() such that $F_{\mathcal {R}_{i_0}}(\alpha,\,u)$
such that $F_{\mathcal {R}_{i_0}}(\alpha,\,u)$![]() admits the FD, then $F_{\{ \mathcal {R}_i\}_{i\in I}}(\alpha,\,u)$
admits the FD, then $F_{\{ \mathcal {R}_i\}_{i\in I}}(\alpha,\,u)$![]() admits the FD, as then $\|b(1)\|_{\infty }\leq \|b\|_{R_{i_0}}\leq \|b\|_{\{ \mathcal {R}_i\}_{i\in I}}$
admits the FD, as then $\|b(1)\|_{\infty }\leq \|b\|_{R_{i_0}}\leq \|b\|_{\{ \mathcal {R}_i\}_{i\in I}}$![]() for all $b\in F(\alpha,\,u)$
for all $b\in F(\alpha,\,u)$![]() . For each $i\in I$
. For each $i\in I$![]() , let $\{E_{t}^{\mathcal {R}_i}\}_{t\in G}$
, let $\{E_{t}^{\mathcal {R}_i}\}_{t\in G}$![]() be the FD for $F_{\mathcal {R}_{i}}(\alpha,\,u)$
be the FD for $F_{\mathcal {R}_{i}}(\alpha,\,u)$![]() , and denote by $\{\mathcal {E}_{t}\}_{t\in G}$
, and denote by $\{\mathcal {E}_{t}\}_{t\in G}$![]() the FD for $F_{\{ \mathcal {R}_i\}_{i\in I}}(\alpha,\,u)$
the FD for $F_{\{ \mathcal {R}_i\}_{i\in I}}(\alpha,\,u)$![]() . Note that $\pi (a):=\prod _{i\in I} a$
. Note that $\pi (a):=\prod _{i\in I} a$![]() is an isometric embedding of $F_{\{ \mathcal {R}_i\}_{i\in I}}(\alpha,\,u)$
is an isometric embedding of $F_{\{ \mathcal {R}_i\}_{i\in I}}(\alpha,\,u)$![]() into the direct product $\prod _{i\in I} F_{\mathcal {R}_{i}}(\alpha,\,u)$
into the direct product $\prod _{i\in I} F_{\mathcal {R}_{i}}(\alpha,\,u)$![]() . Moreover, $\prod _{i\in I} \mathcal {E}_{t}= \prod _{i\in I} E_{t}^{\mathcal {R}_i}\circ \pi$
. Moreover, $\prod _{i\in I} \mathcal {E}_{t}= \prod _{i\in I} E_{t}^{\mathcal {R}_i}\circ \pi$![]() (as maps from $F_{\{ \mathcal {R}_i\}_{i\in I}}(\alpha,\,u)$
(as maps from $F_{\{ \mathcal {R}_i\}_{i\in I}}(\alpha,\,u)$![]() to $\prod _{i\in I} C_0(X)$
to $\prod _{i\in I} C_0(X)$![]() ). Thus, $\bigcap _{t\in G}\ker (\mathcal {E}_t)=0$
). Thus, $\bigcap _{t\in G}\ker (\mathcal {E}_t)=0$![]() if $\bigcap _{t\in G}\ker ( E_{t}^{\mathcal {R}_i})=0$
if $\bigcap _{t\in G}\ker ( E_{t}^{\mathcal {R}_i})=0$![]() for all $i\in I$
for all $i\in I$![]() . That is, $F_{\{ \mathcal {R}_i\}_{i\in I}}(\alpha,\,u)$
. That is, $F_{\{ \mathcal {R}_i\}_{i\in I}}(\alpha,\,u)$![]() is reduced if all $F_{\mathcal {R}_{i}}(\alpha,\,u)$
is reduced if all $F_{\mathcal {R}_{i}}(\alpha,\,u)$![]() , $i\in I$
, $i\in I$![]() , are reduced.
, are reduced.
Example 4.11 Let $p,\,q\in [1,\,\infty ]$![]() satisfy $1/p+1/q=1$
satisfy $1/p+1/q=1$![]() , and let $\|\cdot \|_{L^p}$
, and let $\|\cdot \|_{L^p}$![]() and $\|\cdot \|_{L^p,\operatorname {r}}$
and $\|\cdot \|_{L^p,\operatorname {r}}$![]() be norms in $F^p(\alpha,\,u)$
be norms in $F^p(\alpha,\,u)$![]() and $F^p_{\operatorname {r}}(\alpha,\,u)$
and $F^p_{\operatorname {r}}(\alpha,\,u)$![]() , respectively. By remark 2.13, we have $\|a^*\|_{L^p}=\|a\|_{L^q}$
, respectively. By remark 2.13, we have $\|a^*\|_{L^p}=\|a\|_{L^q}$![]() , $\|a^*\|_{L^p,\operatorname {r}}=\|a\|_{L^q,\operatorname {r}}$
, $\|a^*\|_{L^p,\operatorname {r}}=\|a\|_{L^q,\operatorname {r}}$![]() for $a\in F(\alpha,\,u)$
for $a\in F(\alpha,\,u)$![]() . Thus, in the notation of lemma 4.10, we have $\|a\|_{L^p,*}=\max \{\|a\|_{L^p},\,\|a\|_{L^q}\}$
. Thus, in the notation of lemma 4.10, we have $\|a\|_{L^p,*}=\max \{\|a\|_{L^p},\,\|a\|_{L^q}\}$![]() and $\|a\|_{L^p,\operatorname {r},*}=\max \{\|a\|_{L^p,\operatorname {r}},\,\|a\|_{L^q,\operatorname {r}}\}$
and $\|a\|_{L^p,\operatorname {r},*}=\max \{\|a\|_{L^p,\operatorname {r}},\,\|a\|_{L^q,\operatorname {r}}\}$![]() . Hence,
. Hence,
are Banach $*$![]() -algebra crossed products for $(\alpha,\,u)$
-algebra crossed products for $(\alpha,\,u)$![]() . The algebra $F^{p,*}(\alpha,\,u)$
. The algebra $F^{p,*}(\alpha,\,u)$![]() is universal for covariant representions of $(\alpha,\,u)$
is universal for covariant representions of $(\alpha,\,u)$![]() on $\ell ^{\infty }$
on $\ell ^{\infty }$![]() -direct sums of $L^p$
-direct sums of $L^p$![]() and $L^q$
and $L^q$![]() -spaces, while $F^{p,*}_{\operatorname {r}}(\alpha,\,u)$
-spaces, while $F^{p,*}_{\operatorname {r}}(\alpha,\,u)$![]() is its reduced version. The reduced group Banach algebra $B^{p, *}_{\mathrm {r}} (G)$
is its reduced version. The reduced group Banach algebra $B^{p, *}_{\mathrm {r}} (G)$![]() introduced in [Reference Liao and Yu32], see [Reference Phillips37, Definition 1.6], is the special case of $F^{p,*}_{\operatorname {r}}(\alpha,\,u)$
introduced in [Reference Liao and Yu32], see [Reference Phillips37, Definition 1.6], is the special case of $F^{p,*}_{\operatorname {r}}(\alpha,\,u)$![]() where $X=\{x\}$
where $X=\{x\}$![]() and $u\equiv 1$
and $u\equiv 1$![]() . In the context of twisted groupoids, the algebras $F^{p,*}_{\operatorname {r}}(\alpha,\,u)$
. In the context of twisted groupoids, the algebras $F^{p,*}_{\operatorname {r}}(\alpha,\,u)$![]() were studied in [Reference Austad and Ortega3], see [Reference Austad and Ortega3, Definition 3.7]. In particular, we have $F^{1,*}(\alpha,\,u)=F^{1,*}_{\operatorname {r}}(\alpha,\,u)=F^{\infty,*}(\alpha,\,u)=F^{\infty,*}_{\operatorname {r}}(\alpha,\,u)$
were studied in [Reference Austad and Ortega3], see [Reference Austad and Ortega3, Definition 3.7]. In particular, we have $F^{1,*}(\alpha,\,u)=F^{1,*}_{\operatorname {r}}(\alpha,\,u)=F^{\infty,*}(\alpha,\,u)=F^{\infty,*}_{\operatorname {r}}(\alpha,\,u)$![]() and this $*$
and this $*$![]() -Banach algebra is equipped with the so-called Hahn's $I$
-Banach algebra is equipped with the so-called Hahn's $I$![]() -norm $\|\cdot \|_{I}$
-norm $\|\cdot \|_{I}$![]() considered by a number of authors (cf. [Reference Bardadyn, Kwaśniewski and Mckee6], [Reference Austad and Ortega3], and the sources cited there). We denote this $*$
considered by a number of authors (cf. [Reference Bardadyn, Kwaśniewski and Mckee6], [Reference Austad and Ortega3], and the sources cited there). We denote this $*$![]() -Banach algebra by $F_{I}(\alpha,\,u)$
-Banach algebra by $F_{I}(\alpha,\,u)$![]() and call it Hahn's crossed product.
and call it Hahn's crossed product.
To cover all these examples under one umbrella we will associate crossed products to any set of parameters $P\subseteq [1,\,\infty ]$![]() .
.
Definition 4.12 For any non-empty $P\subseteq [1,\,\infty ]$![]() we put
we put
where $\|b\|_{P}:=\sup _{p\in P}\|b\|_{L^p}$![]() and $\|b\|_{P,\operatorname {r}}:=\sup _{p\in P}\|b\|_{L^p,\operatorname {r}}$
and $\|b\|_{P,\operatorname {r}}:=\sup _{p\in P}\|b\|_{L^p,\operatorname {r}}$![]() , $b\in F(\alpha,\,u)$
, $b\in F(\alpha,\,u)$![]() . We denote by $\Lambda _{P}:F^P(\alpha,\,u)\to F^P_{\operatorname {r}}(\alpha,\,u)$
. We denote by $\Lambda _{P}:F^P(\alpha,\,u)\to F^P_{\operatorname {r}}(\alpha,\,u)$![]() the canonical representation (which is the identity on $F(\alpha,\,u)$
the canonical representation (which is the identity on $F(\alpha,\,u)$![]() ). For convenience we also put
). For convenience we also put
Remark 4.13 For $\emptyset \neq P\subseteq [1,\,\infty ]$![]() , the algebra $F^P(\alpha,\,u)$
, the algebra $F^P(\alpha,\,u)$![]() is universal for representations of $F(\alpha,\,u)$
is universal for representations of $F(\alpha,\,u)$![]() on ($\ell ^{\infty }$
on ($\ell ^{\infty }$![]() -direct sums of) $L^p$
-direct sums of) $L^p$![]() -spaces for all $p\in P$
-spaces for all $p\in P$![]() . By lemma 4.10 and corollary 4.9, $F^P(\alpha,\,u)$
. By lemma 4.10 and corollary 4.9, $F^P(\alpha,\,u)$![]() admits the Fourier decomposition $\{E_{P,t}\}_{t\in G}$
admits the Fourier decomposition $\{E_{P,t}\}_{t\in G}$![]() and $\bigcap _{t\in G}\ker (E_{P,t})=\ker \Lambda _P$
and $\bigcap _{t\in G}\ker (E_{P,t})=\ker \Lambda _P$![]() . Similarly, $F^P_{\operatorname {r}}(\alpha,\,u)$
. Similarly, $F^P_{\operatorname {r}}(\alpha,\,u)$![]() is a reduced crossed product that can be isometrically represented on the $\ell ^{\infty }$
is a reduced crossed product that can be isometrically represented on the $\ell ^{\infty }$![]() -direct sum of spaces $\ell ^p(X\times G)$
-direct sum of spaces $\ell ^p(X\times G)$![]() , $p\in P$
, $p\in P$![]() . When $P=\{p\}$
. When $P=\{p\}$![]() is a singleton we recover the $L^p$
is a singleton we recover the $L^p$![]() -operator algebra crossed products from definition 2.12. When $P=\{p,\,q\}$
-operator algebra crossed products from definition 2.12. When $P=\{p,\,q\}$![]() with $1/p+1/q=1$
with $1/p+1/q=1$![]() we get the Banach $*$
we get the Banach $*$![]() -algebra crossed products from example 4.11. In general, $F^P(\alpha,\,u)$
-algebra crossed products from example 4.11. In general, $F^P(\alpha,\,u)$![]() is a Banach $*$
is a Banach $*$![]() -algebra whenever the set $1/P:=\{1/p:p\in P\}$
-algebra whenever the set $1/P:=\{1/p:p\in P\}$![]() is symmetric with respect to $1/2$
is symmetric with respect to $1/2$![]() . If $\{1,\,\infty \}\subseteq P$
. If $\{1,\,\infty \}\subseteq P$![]() , then $F^P(\alpha,\,u)=F^P_{\operatorname {r}}(\alpha,\,u)=F_{I}(\alpha,\,u)$
, then $F^P(\alpha,\,u)=F^P_{\operatorname {r}}(\alpha,\,u)=F_{I}(\alpha,\,u)$![]() is the Hahn's crossed product, by remark 2.13.
is the Hahn's crossed product, by remark 2.13.
Corollary 4.14 For any non-empty $P\subseteq [1,\,\infty ]$![]() and any $b\in F(\alpha,\,u)$
and any $b\in F(\alpha,\,u)$![]() we have
we have
If $P\subseteq \{1,\,\infty \}$![]() , then $F^P(\alpha,\,u)=F^P_{\operatorname {r}}(\alpha,\,u)$
, then $F^P(\alpha,\,u)=F^P_{\operatorname {r}}(\alpha,\,u)$![]() . If the action $\varphi$
. If the action $\varphi$![]() is amenable, then $F^P(\alpha,\,u)=F^P_{\operatorname {r}}(\alpha,\,u)$
is amenable, then $F^P(\alpha,\,u)=F^P_{\operatorname {r}}(\alpha,\,u)$![]() for any $P\subseteq [1,\,\infty ]$
for any $P\subseteq [1,\,\infty ]$![]() .
.
5. Topological freeness and intersection properties
The term topological freeness was probably coined by Tomiyama. However, the condition appeared much earlier in the work of Zeller–Meier where it was used to characterize when the coefficient algebra is maximal abelian in the reduced $C^*$![]() -algebra crossed product. We generalize this to Banach algebras.
-algebra crossed product. We generalize this to Banach algebras.
Definition 5.1 cf. [Reference Tomiyama41, Definition 2.1(c)]
We call $\varphi$![]() topologically free if the sets $\{ x\in X: \varphi _t(x)=x\}$
topologically free if the sets $\{ x\in X: \varphi _t(x)=x\}$![]() , $t\in G\setminus \{1\}$
, $t\in G\setminus \{1\}$![]() , have empty interiors.
, have empty interiors.
Proposition 5.2 cf. [Reference Zeller-Meier43, Proposition 4.14]
Let $F_{\mathcal {R}}(\alpha,\,u)$![]() be a reduced crossed product. The algebra $C_0(X)$
be a reduced crossed product. The algebra $C_0(X)$![]() is a maximal commutative subalgebra of $F_{\mathcal {R}}(\alpha,\,u)$
is a maximal commutative subalgebra of $F_{\mathcal {R}}(\alpha,\,u)$![]() if and only if $\varphi$
if and only if $\varphi$![]() is topologically free.
is topologically free.
Proof. If $\varphi$![]() is not topologically free, then there is $t\in G\setminus \{1\}$
is not topologically free, then there is $t\in G\setminus \{1\}$![]() and a non-zero $a\in C_0(X)$
and a non-zero $a\in C_0(X)$![]() with $\operatorname {supp}(a):=\overline {\{x:a(x)\neq 0\}}\subseteq \{x\in X:\varphi _t(x)=x\}$
with $\operatorname {supp}(a):=\overline {\{x:a(x)\neq 0\}}\subseteq \{x\in X:\varphi _t(x)=x\}$![]() . Then $b:=av_t\notin C_0(X)$
. Then $b:=av_t\notin C_0(X)$![]() and $b$
and $b$![]() commutes with every $f\in C_0(X)$
commutes with every $f\in C_0(X)$![]() because $b\cdot f= av_t\cdot f= a\alpha _t(f) v_{t}=f a v_t= f \cdot b$
because $b\cdot f= av_t\cdot f= a\alpha _t(f) v_{t}=f a v_t= f \cdot b$![]() . So $C_0(X)$
. So $C_0(X)$![]() is not maximal abelian subalgebra of $F_{\mathcal {R}}(\alpha,\,u)$
is not maximal abelian subalgebra of $F_{\mathcal {R}}(\alpha,\,u)$![]() (here $F_{\mathcal {R}}(\alpha,\,u)$
(here $F_{\mathcal {R}}(\alpha,\,u)$![]() does not need to be reduced). Conversely, assume that $C_0(X)$
does not need to be reduced). Conversely, assume that $C_0(X)$![]() is not a maximal abelian subalgebra of $F_{\mathcal {R}}(\alpha,\,u)$
is not a maximal abelian subalgebra of $F_{\mathcal {R}}(\alpha,\,u)$![]() , and let $b\in F_{\mathcal {R}}(\alpha,\,u) \setminus C_0(X)$
, and let $b\in F_{\mathcal {R}}(\alpha,\,u) \setminus C_0(X)$![]() commute with all elements in $C_0(X)$
commute with all elements in $C_0(X)$![]() . Since $b\not \in C_0(X)$
. Since $b\not \in C_0(X)$![]() and $F_{\mathcal {R}}(\alpha,\,u)$
and $F_{\mathcal {R}}(\alpha,\,u)$![]() is reduced, there is $t\in G\setminus \{1\}$
is reduced, there is $t\in G\setminus \{1\}$![]() such that $E_t(b)\neq 0$
such that $E_t(b)\neq 0$![]() . For any $f\in C_0(X)$
. For any $f\in C_0(X)$![]() , using (4.1) and that $b$
, using (4.1) and that $b$![]() commutes with $f$
commutes with $f$![]() we get $f E_t(b)= E_t(fb)= E_t(bf)=E_t(b)\alpha _t(f)$
we get $f E_t(b)= E_t(fb)= E_t(bf)=E_t(b)\alpha _t(f)$![]() , which implies that $\operatorname {supp}(E_t(b))\subseteq \{x\in X:\varphi _t(x)=x\}$
, which implies that $\operatorname {supp}(E_t(b))\subseteq \{x\in X:\varphi _t(x)=x\}$![]() . Hence $\varphi$
. Hence $\varphi$![]() is not topologically free.
is not topologically free.
Topological freeness implies what in the context of $C^*$![]() -algebras Rørdam calls the pinching property, see [Reference Rørdam39, Definition 3.13]. We use it to show that any Banach algebra completion of $F(\alpha,\,u)$
-algebras Rørdam calls the pinching property, see [Reference Rørdam39, Definition 3.13]. We use it to show that any Banach algebra completion of $F(\alpha,\,u)$![]() (in fact any Hausdorff completion into which $C_0(X)$
(in fact any Hausdorff completion into which $C_0(X)$![]() embeds) admits the Fourier decomposition.
embeds) admits the Fourier decomposition.
Lemma 5.3 pinching property
If $\varphi$![]() is topologically free, then for every $b\in F(\alpha,\,u)$
is topologically free, then for every $b\in F(\alpha,\,u)$![]() , $t\in G$
, $t\in G$![]() , and $\varepsilon >0$
, and $\varepsilon >0$![]() there exists $h\in C_c(X)^+$
there exists $h\in C_c(X)^+$![]() of norm one such that
of norm one such that
Proof. For $t=1$![]() this follows by (the proof of) [Reference Exel, Laca and Quigg17, Proposition 2.4]. For general $t\in G$
this follows by (the proof of) [Reference Exel, Laca and Quigg17, Proposition 2.4]. For general $t\in G$![]() we may use that $E_t(b)=\lim _{i} E_1(b \cdot (\mu _i \delta _{t})^*)$
we may use that $E_t(b)=\lim _{i} E_1(b \cdot (\mu _i \delta _{t})^*)$![]() for any contractive approximate unit $(\mu _i)$
for any contractive approximate unit $(\mu _i)$![]() in $C_0(X)$
in $C_0(X)$![]() . Namely, putting $b_i:=b \cdot (\mu _i \delta _{t})^*$
. Namely, putting $b_i:=b \cdot (\mu _i \delta _{t})^*$![]() from some point on we have $\|E_t(b)-E_1(b_i)\|\leq \varepsilon /3$
from some point on we have $\|E_t(b)-E_1(b_i)\|\leq \varepsilon /3$![]() , and by the previous remark we may find a norm one $h\in C_c(X)^+$
, and by the previous remark we may find a norm one $h\in C_c(X)^+$![]() such that $\|E_1(b_i)\|\leq \| hE_1(b_i)h\|+\varepsilon /3$
such that $\|E_1(b_i)\|\leq \| hE_1(b_i)h\|+\varepsilon /3$![]() and $\|hE_1(b_i)h-hb_ih\|\leq \varepsilon /3.$
and $\|hE_1(b_i)h-hb_ih\|\leq \varepsilon /3.$![]() Using these three inequalities we get
Using these three inequalities we get
Since $\lim _{i}b_ih =b (h\delta _t)^*$![]() we get the assertion.
we get the assertion.
Lemma 5.4 [Reference Bonsall8, Theorem 10]
If $A$![]() is a $C^*$
is a $C^*$![]() -algebra, so in particular, if $A=C_0(X)$
-algebra, so in particular, if $A=C_0(X)$![]() , then any injective representation $\psi : A\to B$
, then any injective representation $\psi : A\to B$![]() into a Banach algebra $B$
into a Banach algebra $B$![]() is isometric.
is isometric.
Proposition 5.5 Assume that $\varphi$![]() is topologically free and let $F_{\mathcal {R}}(\alpha,\,u)$
is topologically free and let $F_{\mathcal {R}}(\alpha,\,u)$![]() be a crossed product. For any representation $\psi :F_{\mathcal {R}}(\alpha,\,u)\to B$
be a crossed product. For any representation $\psi :F_{\mathcal {R}}(\alpha,\,u)\to B$![]() which is injective on $C_0(X)$
which is injective on $C_0(X)$![]() and has dense range, there are contractive linear maps $E^{\psi }_{t}:B\to C_0(X)$
and has dense range, there are contractive linear maps $E^{\psi }_{t}:B\to C_0(X)$![]() , $t\in G$
, $t\in G$![]() , such that $E^{\psi }_{t}(\psi (b))=E_t^{\mathcal {R}}(b)$
, such that $E^{\psi }_{t}(\psi (b))=E_t^{\mathcal {R}}(b)$![]() for $b\in F_{\mathcal {R}}(\alpha,\,u)$
for $b\in F_{\mathcal {R}}(\alpha,\,u)$![]() , $t\in G$
, $t\in G$![]() . In particular, $\ker \psi \subseteq \bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$
. In particular, $\ker \psi \subseteq \bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$![]() .
.
Proof. Fix $t\in G$![]() . Take any $b\in F(\alpha,\,u)\subseteq F_{\mathcal {R}}(\alpha,\,u)$
. Take any $b\in F(\alpha,\,u)\subseteq F_{\mathcal {R}}(\alpha,\,u)$![]() and $\varepsilon >0$
and $\varepsilon >0$![]() . Let $h\in C_c(X)^+$
. Let $h\in C_c(X)^+$![]() be as in lemma 5.3. Using that $\psi$
be as in lemma 5.3. Using that $\psi$![]() is isometric on $C_0(X)$
is isometric on $C_0(X)$![]() , by lemma 5.4, we get
, by lemma 5.4, we get

This shows that $\|E_t^{\mathcal {R}}(b)\|\leq \|\psi (b)\|$![]() . Hence, the formula $E^{\psi }_{t}(\psi (b)):=E_t^{\mathcal {R}}(b)$
. Hence, the formula $E^{\psi }_{t}(\psi (b)):=E_t^{\mathcal {R}}(b)$![]() , $b\in F(\alpha,\,u)$
, $b\in F(\alpha,\,u)$![]() , yields a well-defined linear contraction $\psi (F(\alpha,\,u))\to C_0(X)$
, yields a well-defined linear contraction $\psi (F(\alpha,\,u))\to C_0(X)$![]() which extends to the contraction $E^{\psi }_{t}:B\to C_0(X)$
which extends to the contraction $E^{\psi }_{t}:B\to C_0(X)$![]() satisfying $E^{\psi }_{t}(\psi (b))=E_t^{\mathcal {R}}(b)$
satisfying $E^{\psi }_{t}(\psi (b))=E_t^{\mathcal {R}}(b)$![]() for $b\in F_{\mathcal {R}}(\alpha,\,u)$
for $b\in F_{\mathcal {R}}(\alpha,\,u)$![]() .
.
The relationship between topological freeness and ideals in $C^*$![]() -crossed products was probably first made explicit by O'Donovan, for $\mathbb {Z}$
-crossed products was probably first made explicit by O'Donovan, for $\mathbb {Z}$![]() -actions, see [Reference O'Donovan33, Theorem 1.2.1]. Sierakowski in [Reference Sierakowski40] called the relevant condition the intersection property.
-actions, see [Reference O'Donovan33, Theorem 1.2.1]. Sierakowski in [Reference Sierakowski40] called the relevant condition the intersection property.
Definition 5.6 cf. [Reference Kwaśniewski and Meyer30, Definitions 5.5, 5.6]
An inclusion of Banach algebras $A\subseteq B$![]() has the generalized intersection property if there is the largest ideal $\operatorname {\mathcal {N}}$
has the generalized intersection property if there is the largest ideal $\operatorname {\mathcal {N}}$![]() in $B$
in $B$![]() with $\operatorname {\mathcal {N}}\cap A=\{0\}$
with $\operatorname {\mathcal {N}}\cap A=\{0\}$![]() . Then we call $\operatorname {\mathcal {N}}$
. Then we call $\operatorname {\mathcal {N}}$![]() the hidden ideal for $A\subseteq B$
the hidden ideal for $A\subseteq B$![]() . If $\operatorname {\mathcal {N}}=\{0\}$
. If $\operatorname {\mathcal {N}}=\{0\}$![]() , that is if for every non-zero ideal $J$
, that is if for every non-zero ideal $J$![]() in $B$
in $B$![]() we have $J\cap A \neq \{0\}$
we have $J\cap A \neq \{0\}$![]() we say that $A\subseteq B$
we say that $A\subseteq B$![]() has the intersection property or that the subalgebra $A$
has the intersection property or that the subalgebra $A$![]() detects ideals in the algebra $B$
detects ideals in the algebra $B$![]() .
.
Remark 5.7 By the last part of lemma 4.2, if $F_{\mathcal {R}}(\alpha,\,u)$![]() is a Banach algebra crossed product and $C_0(X)$
is a Banach algebra crossed product and $C_0(X)$![]() detects ideals in $F_{\mathcal {R}}(\alpha,\,u)$
detects ideals in $F_{\mathcal {R}}(\alpha,\,u)$![]() , then $F_{\mathcal {R}}(\alpha,\,u)$
, then $F_{\mathcal {R}}(\alpha,\,u)$![]() is necessarily reduced.
is necessarily reduced.
Clearly $A\subseteq B$![]() has the generalized intersection property with hidden ideal $\operatorname {\mathcal {N}}$
has the generalized intersection property with hidden ideal $\operatorname {\mathcal {N}}$![]() if and only if any representation $\pi :B\to C$
if and only if any representation $\pi :B\to C$![]() injective on $A$
injective on $A$![]() descends to a (necessarily injective) representation $B/\operatorname {\mathcal {N}}\to C$
descends to a (necessarily injective) representation $B/\operatorname {\mathcal {N}}\to C$![]() . Thus, proposition 5.5 immediately gives
. Thus, proposition 5.5 immediately gives
Corollary 5.8 If $\varphi$![]() is topologically free, then for any crossed product $F_{\mathcal {R}}(\alpha,\,u)$
is topologically free, then for any crossed product $F_{\mathcal {R}}(\alpha,\,u)$![]() the inclusion $C_0(X)\subseteq F_{\mathcal {R}}(\alpha,\,u)$
the inclusion $C_0(X)\subseteq F_{\mathcal {R}}(\alpha,\,u)$![]() has the generalized intersection property with the hidden ideal $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$
has the generalized intersection property with the hidden ideal $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$![]() ; in particular, $C_0(X)$
; in particular, $C_0(X)$![]() detects ideals in all reduced crossed products.
detects ideals in all reduced crossed products.
When applied to untwisted crossed products that have ‘$C_0(X)$![]() -trivial representations’, the implication in the above corollary can be reversed. For $C^*$
-trivial representations’, the implication in the above corollary can be reversed. For $C^*$![]() -algebraic crossed products this was proved in [Reference Kawamura and Tomiyama27, Theorem 4.1], [Reference Archbold and Spielberg4, Theorem 2]. We now generalize these results to crossed products $F^P(\alpha,\,u)$
-algebraic crossed products this was proved in [Reference Kawamura and Tomiyama27, Theorem 4.1], [Reference Archbold and Spielberg4, Theorem 2]. We now generalize these results to crossed products $F^P(\alpha,\,u)$![]() where $P\subseteq [1,\,\infty ]$
where $P\subseteq [1,\,\infty ]$![]() . If $P$
. If $P$![]() is non-empty, we define the $C_0(X)$
is non-empty, we define the $C_0(X)$![]() -trivial representation $\Lambda _{P}^{\operatorname {tr}}$
-trivial representation $\Lambda _{P}^{\operatorname {tr}}$![]() of $F^P (\alpha )$
of $F^P (\alpha )$![]() as an extension of the $\ell ^{\infty }$
as an extension of the $\ell ^{\infty }$![]() -direct sum $\oplus _{p\in P}\Lambda _p^{\operatorname {tr}}$
-direct sum $\oplus _{p\in P}\Lambda _p^{\operatorname {tr}}$![]() of representations from example 2.14. We also put $\Lambda _{\emptyset }^{\operatorname {tr}}:=\Lambda _{[1,\infty ]}^{\operatorname {tr}}|_{F (\alpha )}$
of representations from example 2.14. We also put $\Lambda _{\emptyset }^{\operatorname {tr}}:=\Lambda _{[1,\infty ]}^{\operatorname {tr}}|_{F (\alpha )}$![]() and recall that $F^\emptyset (\alpha )=F (\alpha )$
and recall that $F^\emptyset (\alpha )=F (\alpha )$![]() .
.
Theorem 5.9 Let $\alpha$![]() be an action of a discrete group $G$
be an action of a discrete group $G$![]() on $C_0(X)$
on $C_0(X)$![]() . For any $P\subseteq [1,\,\infty ]$
. For any $P\subseteq [1,\,\infty ]$![]() , the following conditions are equivalent:
, the following conditions are equivalent:
(1) The dual action $\varphi$
 of $G$
of $G$ on $X$
on $X$ is topologically free.
is topologically free.(2) $C_0(X)\subseteq F^P(\alpha )$
 has the generalized intersection property with the hidden ideal being the kernel of $\Lambda _P:F^P (\alpha )\to F_{\operatorname {r}}^P (\alpha )$
has the generalized intersection property with the hidden ideal being the kernel of $\Lambda _P:F^P (\alpha )\to F_{\operatorname {r}}^P (\alpha )$ .
.(3) $\ker (\Lambda _P^{\operatorname {tr}})\subseteq \ker (\Lambda _P)$
 where $\Lambda _{P}^{\operatorname {tr}}$
where $\Lambda _{P}^{\operatorname {tr}}$ is the $C_0(X)$
is the $C_0(X)$ -trivial representation of $F^P (\alpha )$
-trivial representation of $F^P (\alpha )$ .
.(4) $C_0(X)$
 detects ideals in $F^T(\alpha )$
detects ideals in $F^T(\alpha )$ for some (and hence all) $T\subseteq \{1,\,\infty \}$
for some (and hence all) $T\subseteq \{1,\,\infty \}$ .
.
Proof. (1) implies (2) by corollary 5.8 and remark 4.13. (2) implies (3) because $\ker (\Lambda _P^{\operatorname {tr}})\cap C_0(X)=\{0\}$![]() . To show that (3) implies (1) assume that $\varphi$
. To show that (3) implies (1) assume that $\varphi$![]() is not topologically free. Then there are $t\in G\setminus \{1\}$
is not topologically free. Then there are $t\in G\setminus \{1\}$![]() and an open non-empty set $U\subseteq X$
and an open non-empty set $U\subseteq X$![]() such that $\varphi _t|_{U}=\text {id}_{U}$
such that $\varphi _t|_{U}=\text {id}_{U}$![]() . Take any non-zero $a\in C_0(U)\subseteq C_0(X)$
. Take any non-zero $a\in C_0(U)\subseteq C_0(X)$![]() . Then $b:=a-\delta _{t^{-1}}a\in F(\alpha )$
. Then $b:=a-\delta _{t^{-1}}a\in F(\alpha )$![]() is non-zero, and so $\Lambda _P(b)\neq 0$
is non-zero, and so $\Lambda _P(b)\neq 0$![]() , but (2.5) readily implies that $\Lambda _P^{\operatorname {tr}}(b)=0$
, but (2.5) readily implies that $\Lambda _P^{\operatorname {tr}}(b)=0$![]() . Hence, $\ker (\Lambda _P^{\operatorname {tr}})\not \subseteq \ker (\Lambda _P)$
. Hence, $\ker (\Lambda _P^{\operatorname {tr}})\not \subseteq \ker (\Lambda _P)$![]() . Thus, (1)–(3) are equivalent. These conditions are independent of $P$
. Thus, (1)–(3) are equivalent. These conditions are independent of $P$![]() because (1) is. Condition (4) is equivalent to (2) for $P=T$
because (1) is. Condition (4) is equivalent to (2) for $P=T$![]() , because $F^T(\alpha )=F^T_{\operatorname {r}}(\alpha )$
, because $F^T(\alpha )=F^T_{\operatorname {r}}(\alpha )$![]() by corollary 4.14. Hence, all conditions (1)–(4) are equivalent.
by corollary 4.14. Hence, all conditions (1)–(4) are equivalent.
Corollary 5.10 For any $P\subseteq [1,\,\infty ]$![]() , $C_0(X)$
, $C_0(X)$![]() detects ideals in $F^P(\alpha )$
detects ideals in $F^P(\alpha )$![]() if and only if the regular representation $\Lambda _P$
if and only if the regular representation $\Lambda _P$![]() is injective and $\varphi$
is injective and $\varphi$![]() is topologically free.
is topologically free.
Proof. Since $\ker (\Lambda _P)\cap C_0(X)=\{0\}$![]() , we see that $C_0(X)$
, we see that $C_0(X)$![]() detects ideals in $F^P(\alpha )$
detects ideals in $F^P(\alpha )$![]() if and only if $\ker (\Lambda _P)=\{0\}$
if and only if $\ker (\Lambda _P)=\{0\}$![]() and condition (2) in theorem 5.9 holds.
and condition (2) in theorem 5.9 holds.
By corollary 5.8, topological freeness implies that $C_0(X)$![]() detects ideals in every reduced algebra $F^p_{\operatorname {r}}(\alpha )$
detects ideals in every reduced algebra $F^p_{\operatorname {r}}(\alpha )$![]() , $p\in (1,\,\infty )$
, $p\in (1,\,\infty )$![]() , but in general (when the action is not amenable) the converse is not true. For instance, the main result of [Reference Hejazian and Pooya25] implies that if $G$
, but in general (when the action is not amenable) the converse is not true. For instance, the main result of [Reference Hejazian and Pooya25] implies that if $G$![]() is a group with the Powers property (so for instance, a free group $G=\mathbb {F}_n$
is a group with the Powers property (so for instance, a free group $G=\mathbb {F}_n$![]() with $n>1$
with $n>1$![]() generators), then for any minimal action $\varphi$
generators), then for any minimal action $\varphi$![]() on a compact space $X$
on a compact space $X$![]() the crossed products $F^p_{\operatorname {r}}(\alpha )$
the crossed products $F^p_{\operatorname {r}}(\alpha )$![]() , $p\in (1,\,\infty )$
, $p\in (1,\,\infty )$![]() , are simple, and so $C_0(X)$
, are simple, and so $C_0(X)$![]() detects ideals in $F^p_{\operatorname {r}}(\alpha )$
detects ideals in $F^p_{\operatorname {r}}(\alpha )$![]() but the action might be trivial. This in particular applies to actions on $X=\{x\}$
but the action might be trivial. This in particular applies to actions on $X=\{x\}$![]() . Then the resulting crossed products are group Banach algebras that we denote by $F(G,\,u)$
. Then the resulting crossed products are group Banach algebras that we denote by $F(G,\,u)$![]() , $F_{\operatorname {r}}^p(G,\,u)$
, $F_{\operatorname {r}}^p(G,\,u)$![]() and so on. For group algebras Phillips extended in [Reference Phillips37] the result of [Reference Hejazian and Pooya25] to all $C^*$
and so on. For group algebras Phillips extended in [Reference Phillips37] the result of [Reference Hejazian and Pooya25] to all $C^*$![]() -simple groups. So for ‘large groups’ topological freeness is not necessary for simplicity of $F^p_{\operatorname {r}}(\alpha )$
-simple groups. So for ‘large groups’ topological freeness is not necessary for simplicity of $F^p_{\operatorname {r}}(\alpha )$![]() . Adding a twist to the picture makes things even more interesting, as then topological freeness is not necessary even for simplicity of algebras of finite abelian groups:
. Adding a twist to the picture makes things even more interesting, as then topological freeness is not necessary even for simplicity of algebras of finite abelian groups:
Example 5.11 Any matrix algebra $M_{n}(\mathbb {C})$![]() is a twisted group algebra where $G:=\mathbb {Z}_n\times \mathbb {Z}_n$
is a twisted group algebra where $G:=\mathbb {Z}_n\times \mathbb {Z}_n$![]() and $u( (p ,\,r),\, (s,\,t)):=e^{-2\pi i {rs}/{n}}$
and $u( (p ,\,r),\, (s,\,t)):=e^{-2\pi i {rs}/{n}}$![]() , $p,\,r,\,s,\,t\in \mathbb {Z}_n$
, $p,\,r,\,s,\,t\in \mathbb {Z}_n$![]() . The identification (that disregards norms) goes via the map $F(G,\,u)\ni a\mapsto \overline {a}\in M_{n}(\mathbb {C})$
. The identification (that disregards norms) goes via the map $F(G,\,u)\ni a\mapsto \overline {a}\in M_{n}(\mathbb {C})$![]() where $(\overline {a}x)(r):=\sum _{s,t\in \mathbb {Z}_n} a(s,\,t)e^{2\pi i ({rs}/{n})} x(r-t)$
where $(\overline {a}x)(r):=\sum _{s,t\in \mathbb {Z}_n} a(s,\,t)e^{2\pi i ({rs}/{n})} x(r-t)$![]() for $x=(x(1),\,\ldots,\,x(n))\in \mathbb {C}^n$
for $x=(x(1),\,\ldots,\,x(n))\in \mathbb {C}^n$![]() and $r=1,\,\ldots,\,n$
and $r=1,\,\ldots,\,n$![]() . Note that functions supported on the subgroup $H:=\mathbb {Z}_n\times \{0\}$
. Note that functions supported on the subgroup $H:=\mathbb {Z}_n\times \{0\}$![]() form a subalgebra of diagonal matrices in $F(G,\,u)=M_{n}(\mathbb {C})$
form a subalgebra of diagonal matrices in $F(G,\,u)=M_{n}(\mathbb {C})$![]() that can be identified with $F(H)$
that can be identified with $F(H)$![]() . In particular, $\mathbb {C}\cdot 1$
. In particular, $\mathbb {C}\cdot 1$![]() detects ideals in $F(G,\,u)$
detects ideals in $F(G,\,u)$![]() , because $F(G,\,u)$
, because $F(G,\,u)$![]() is simple, but $\mathbb {C}\cdot 1$
is simple, but $\mathbb {C}\cdot 1$![]() does not detect ideals in $F(H) \subseteq F(G,\,u)$
does not detect ideals in $F(H) \subseteq F(G,\,u)$![]() , unless $n=1$
, unless $n=1$![]() .
.
We now show that the only reason why topological freeness fails in the above examples is that it passes to subgroups while detection of ideals does not pass to subalgebras (not even those coming from subgroups). Namely, let $H\subseteq G$![]() be a subgroup of $G$
be a subgroup of $G$![]() . Topological freeness of $\varphi :G\to \operatorname {Homeo}(X)$
. Topological freeness of $\varphi :G\to \operatorname {Homeo}(X)$![]() implies topological freeness of the restricted action $\varphi |_{H}:H\to \operatorname {Homeo}(X)$
implies topological freeness of the restricted action $\varphi |_{H}:H\to \operatorname {Homeo}(X)$![]() . Also any twisted action $(\alpha,\,u)$
. Also any twisted action $(\alpha,\,u)$![]() of $G$
of $G$![]() restricts to a twisted action $(\alpha |_H,\,u|_H)$
restricts to a twisted action $(\alpha |_H,\,u|_H)$![]() of $H$
of $H$![]() (formally we should write $u|_{H\times H}$
(formally we should write $u|_{H\times H}$![]() ). Clearly, $F(\alpha |_H,\,u|_H)\subseteq F(\alpha,\,u)$
). Clearly, $F(\alpha |_H,\,u|_H)\subseteq F(\alpha,\,u)$![]() . If $\mathcal {R}$
. If $\mathcal {R}$![]() is a class of representations of $F(\alpha,\,u)$
is a class of representations of $F(\alpha,\,u)$![]() , we denote by $\mathcal {R}|_H$
, we denote by $\mathcal {R}|_H$![]() their restrictions to $F(\alpha |_H,\,u|_H)$
their restrictions to $F(\alpha |_H,\,u|_H)$![]() . Then $F_{\mathcal {R}|_{H}}(\alpha |_{H},\,u|_{H})\subseteq F_{\mathcal {R}}(\alpha,\,u)$
. Then $F_{\mathcal {R}|_{H}}(\alpha |_{H},\,u|_{H})\subseteq F_{\mathcal {R}}(\alpha,\,u)$![]() is a Banach subalgebra, and $F_{\mathcal {R}|_{H}}(\alpha |_{H},\,u|_{H})$
is a Banach subalgebra, and $F_{\mathcal {R}|_{H}}(\alpha |_{H},\,u|_{H})$![]() admits the FD or is reduced if $F_{\mathcal {R}}(\alpha,\,u)$
admits the FD or is reduced if $F_{\mathcal {R}}(\alpha,\,u)$![]() has this property. This applies to full crossed products in definition 4.12 giving $F^P(\alpha |_{H},\,u|_{H})\subseteq F^P(\alpha,\,u)$
has this property. This applies to full crossed products in definition 4.12 giving $F^P(\alpha |_{H},\,u|_{H})\subseteq F^P(\alpha,\,u)$![]() for any $P\subseteq [1,\,\infty ]$
for any $P\subseteq [1,\,\infty ]$![]() . For reduced crossed products this is not clear. We certainly have $F^P_{\operatorname {r}}(\alpha |_{H},\,u|_{H})\subseteq F^P_{\operatorname {r}}(\alpha,\,u)$
. For reduced crossed products this is not clear. We certainly have $F^P_{\operatorname {r}}(\alpha |_{H},\,u|_{H})\subseteq F^P_{\operatorname {r}}(\alpha,\,u)$![]() when $P\subseteq \{1,\,2,\,\infty \}$
when $P\subseteq \{1,\,2,\,\infty \}$![]() (as for $p=1,\,\infty$
(as for $p=1,\,\infty$![]() the reduced and full crossed products coincide, and for $p=2$
the reduced and full crossed products coincide, and for $p=2$![]() the inclusion is a well-known $C^*$
the inclusion is a well-known $C^*$![]() -algebraic fact). We also have $F^P_{\operatorname {r}}(\alpha |_{H},\,u|_{H})\subseteq F^P_{\operatorname {r}}(\alpha,\,u)$
-algebraic fact). We also have $F^P_{\operatorname {r}}(\alpha |_{H},\,u|_{H})\subseteq F^P_{\operatorname {r}}(\alpha,\,u)$![]() whenever $F^P_{\operatorname {r}}(\alpha |_{H},\,u|_{H})=F^P(\alpha |_{H},\,u|_{H})$
whenever $F^P_{\operatorname {r}}(\alpha |_{H},\,u|_{H})=F^P(\alpha |_{H},\,u|_{H})$![]() , which holds for instance when the restricted action $\varphi |_{H}$
, which holds for instance when the restricted action $\varphi |_{H}$![]() is amenable.
is amenable.
The next result is inspired by the corresponding result in [Reference Kwaśniewski and Meyer31] proved for $C^*$![]() -algebras associated to Fell bundles over inverse semigroups, cf. [Reference Kwaśniewski and Meyer31, Proposition 6.4].
-algebras associated to Fell bundles over inverse semigroups, cf. [Reference Kwaśniewski and Meyer31, Proposition 6.4].
Theorem 5.12 Let $(\alpha,\,u)$![]() be a twisted action of a discrete group $G$
be a twisted action of a discrete group $G$![]() on $C_0(X)$
on $C_0(X)$![]() . For any $P\subseteq [1,\,\infty ]$
. For any $P\subseteq [1,\,\infty ]$![]() , the following conditions are equivalent:
, the following conditions are equivalent:
(1) The dual action $\varphi :G\to \operatorname {Homeo}(X)$
 is topologically free.
is topologically free.(2) For any subgroup $H\subseteq G$
 , $C_0(X)\subseteq F^P (\alpha |_{H},\,u|_{H})$
, $C_0(X)\subseteq F^P (\alpha |_{H},\,u|_{H})$ has the generalized intersection property with hidden ideal being the kernel of $\Lambda _P:F^P (\alpha |_{H},\,u|_{H})\to F_{\operatorname {r}}^P (\alpha |_{H},\,u|_{H})$
has the generalized intersection property with hidden ideal being the kernel of $\Lambda _P:F^P (\alpha |_{H},\,u|_{H})\to F_{\operatorname {r}}^P (\alpha |_{H},\,u|_{H})$ .
.(3) $C_0(X)$
 detects ideals in all $F_{\operatorname {r}}^P (\alpha |_{H},\,u|_{H})$
detects ideals in all $F_{\operatorname {r}}^P (\alpha |_{H},\,u|_{H})$ for any subgroup $H\subseteq G$
for any subgroup $H\subseteq G$ .
.(4) $C_0(X)$
 detects ideals in all $F_{\operatorname {r}}^P (\alpha |_{H},\,u|_{H})$
detects ideals in all $F_{\operatorname {r}}^P (\alpha |_{H},\,u|_{H})$ for any cyclic subgroup $H\subseteq G$
for any cyclic subgroup $H\subseteq G$ .
.
Corollary 5.13 Assume the action $\varphi$![]() is amenable and let $u\in Z^2(G,\, C_u(X))$
is amenable and let $u\in Z^2(G,\, C_u(X))$![]() and $P\subseteq [1,\,\infty ]$
and $P\subseteq [1,\,\infty ]$![]() . Then $\varphi$
. Then $\varphi$![]() is topologically free if and only if $C_0(X)$
is topologically free if and only if $C_0(X)$![]() detects ideals in all intermediate subalgebras $F^P (\alpha |_{H},\,u|_{H})\subseteq F^P (\alpha,\,u)$
detects ideals in all intermediate subalgebras $F^P (\alpha |_{H},\,u|_{H})\subseteq F^P (\alpha,\,u)$![]() , where $H\subseteq G$
, where $H\subseteq G$![]() is a subgroup.
is a subgroup.
Proof. Amenability of $\varphi :G\to \operatorname {Homeo}(X)$![]() passes to the restricted action $\varphi :H\to \operatorname {Homeo}(X)$
passes to the restricted action $\varphi :H\to \operatorname {Homeo}(X)$![]() . Hence, $F^P (\alpha |_{H},\,u|_{H})=F_{\operatorname {r}}^P (\alpha |_{H},\,u|_{H})$
. Hence, $F^P (\alpha |_{H},\,u|_{H})=F_{\operatorname {r}}^P (\alpha |_{H},\,u|_{H})$![]() by corollary 4.14. In particular, $F^P (\alpha |_{H},\,u|_{H})$
by corollary 4.14. In particular, $F^P (\alpha |_{H},\,u|_{H})$![]() embeds into $F^P (\alpha,\,u)$
embeds into $F^P (\alpha,\,u)$![]() .
.
For the proof of theorem 5.12 we need some preparations. A set $U\subseteq X$![]() is $\varphi$
is $\varphi$![]() -invariant if $\varphi _{t}(U)=U$
-invariant if $\varphi _{t}(U)=U$![]() for all $t\in G$
for all $t\in G$![]() . For any such set the twisted action $(\alpha,\,u)$
. For any such set the twisted action $(\alpha,\,u)$![]() of $G$
of $G$![]() restricts to a twisted action $(\alpha ^U,\,u^U)$
restricts to a twisted action $(\alpha ^U,\,u^U)$![]() of $G$
of $G$![]() where the action dual to $\alpha ^U$
where the action dual to $\alpha ^U$![]() is given by homeomorphisms $\varphi ^{U}_t:=\varphi _{t}|_{U}$
is given by homeomorphisms $\varphi ^{U}_t:=\varphi _{t}|_{U}$![]() , $t\in G$
, $t\in G$![]() , and we put $u^U(s,\,t):=u(s,\,t)|_{U}$
, and we put $u^U(s,\,t):=u(s,\,t)|_{U}$![]() for $s,\,t\in G$
for $s,\,t\in G$![]() . Assume $U$
. Assume $U$![]() is $\varphi$
is $\varphi$![]() -invariant and open. Then $F(\alpha ^U,\,u^U)=\ell ^1(G,\,C_0(U))\subseteq \ell ^1(G,\,C_0(X))=F(\alpha,\,u)$
-invariant and open. Then $F(\alpha ^U,\,u^U)=\ell ^1(G,\,C_0(U))\subseteq \ell ^1(G,\,C_0(X))=F(\alpha,\,u)$![]() is naturally a $^*$
is naturally a $^*$![]() -Banach subalgebra, and in fact an ideal in $F(\alpha,\,u)$
-Banach subalgebra, and in fact an ideal in $F(\alpha,\,u)$![]() . If $\mathcal {R}$
. If $\mathcal {R}$![]() is a class of representations of $F(\alpha,\,u)$
is a class of representations of $F(\alpha,\,u)$![]() , we denote by $\mathcal {R}^U$
, we denote by $\mathcal {R}^U$![]() their restrictions to $F(\alpha ^U,\,u^U)$
their restrictions to $F(\alpha ^U,\,u^U)$![]() . Then again, $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)\subseteq F_{\mathcal {R}}(\alpha,\,u)$
. Then again, $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)\subseteq F_{\mathcal {R}}(\alpha,\,u)$![]() is an ideal, and $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$
is an ideal, and $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$![]() admits the FD or is reduced if $F_{\mathcal {R}}(\alpha,\,u)$
admits the FD or is reduced if $F_{\mathcal {R}}(\alpha,\,u)$![]() has this property. Modulo compression of the space, this applies to reduced $L^p$
has this property. Modulo compression of the space, this applies to reduced $L^p$![]() -operator algebra crossed products giving $F^P_{\operatorname {r}}(\alpha ^U,\,u^U)\subseteq F^P_{\operatorname {r}}(\alpha,\,u)$
-operator algebra crossed products giving $F^P_{\operatorname {r}}(\alpha ^U,\,u^U)\subseteq F^P_{\operatorname {r}}(\alpha,\,u)$![]() for any $P\subseteq [1,\,\infty ]$
for any $P\subseteq [1,\,\infty ]$![]() . For full crossed products this is not clear. We have $F^P(\alpha ^U,\,u^U)\subseteq F^P(\alpha,\,u)$
. For full crossed products this is not clear. We have $F^P(\alpha ^U,\,u^U)\subseteq F^P(\alpha,\,u)$![]() for $P\subseteq \{1,\,2,\,\infty \}$
for $P\subseteq \{1,\,2,\,\infty \}$![]() , as for $p=1,\,\infty$
, as for $p=1,\,\infty$![]() the reduced and full crossed products coincide and for $p=2$
the reduced and full crossed products coincide and for $p=2$![]() it is a known $C^*$
it is a known $C^*$![]() -algebraic fact, see [Reference Exel16, Proposition 21.15]. For other $P$
-algebraic fact, see [Reference Exel16, Proposition 21.15]. For other $P$![]() we certainly have this whenever $F^P(\alpha ^U,\,u^U)=F^P_{\operatorname {r}}(\alpha ^U,\,u^U)$
we certainly have this whenever $F^P(\alpha ^U,\,u^U)=F^P_{\operatorname {r}}(\alpha ^U,\,u^U)$![]() which holds for instance when the restricted action $\varphi ^{U}:G\to \operatorname {Homeo}(U)$
which holds for instance when the restricted action $\varphi ^{U}:G\to \operatorname {Homeo}(U)$![]() is amenable.
is amenable.
Lemma 5.14 Assume $F_{\mathcal {R}}(\alpha,\,u)$![]() is a Banach algebra crossed product. An ideal in $F_{\mathcal {R}}(\alpha,\,u)$
is a Banach algebra crossed product. An ideal in $F_{\mathcal {R}}(\alpha,\,u)$![]() is generated by its intersection with $C_0(X)$
is generated by its intersection with $C_0(X)$![]() if and only if it is of the form $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$
if and only if it is of the form $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$![]() for some open $\varphi$
for some open $\varphi$![]() -invariant $U\subseteq X$
-invariant $U\subseteq X$![]() , and then $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)\cap C_0(X)=C_0(U)$
, and then $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)\cap C_0(X)=C_0(U)$![]() . If $C_0(X)$
. If $C_0(X)$![]() detects ideals in $F_{\mathcal {R}}(\alpha,\,u)$
detects ideals in $F_{\mathcal {R}}(\alpha,\,u)$![]() , then $C_0(U)$
, then $C_0(U)$![]() detects ideals in $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$
detects ideals in $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$![]() for any open $\varphi$
for any open $\varphi$![]() -invariant $U\subseteq X$
-invariant $U\subseteq X$![]() .
.
Proof. If $J$![]() is an ideal in $F_{\mathcal {R}}(\alpha,\,u)$
is an ideal in $F_{\mathcal {R}}(\alpha,\,u)$![]() , then $J\cap C_0(X)$
, then $J\cap C_0(X)$![]() is an ideal in $C_0(U)$
is an ideal in $C_0(U)$![]() and hence $J\cap C_0(X)=C_0(U)$
and hence $J\cap C_0(X)=C_0(U)$![]() for an open set $U\subseteq X$
for an open set $U\subseteq X$![]() . Disintegrating the identity map on $F_{\mathcal {R}}(\alpha,\,u)$
. Disintegrating the identity map on $F_{\mathcal {R}}(\alpha,\,u)$![]() , see lemma 2.8, and using covariance relations, for any $a\in C_0(U)$
, see lemma 2.8, and using covariance relations, for any $a\in C_0(U)$![]() and $t\in G$
and $t\in G$![]() we get $\alpha _t(a)=v_t a v_{t}^{-1}\in J\cap C_0(X)=C_0(U)$
we get $\alpha _t(a)=v_t a v_{t}^{-1}\in J\cap C_0(X)=C_0(U)$![]() . Hence, $U$
. Hence, $U$![]() is $\varphi$
is $\varphi$![]() -invariant. Now let $U$
-invariant. Now let $U$![]() be any $\varphi$
be any $\varphi$![]() -invariant open set. The ideal generated by $C_0(U)$
-invariant open set. The ideal generated by $C_0(U)$![]() in $F(\alpha,\,u)= \ell ^1(G,\,C_0(X))$
in $F(\alpha,\,u)= \ell ^1(G,\,C_0(X))$![]() is $F(\alpha ^U,\,u^U)=\ell ^1(G,\,C_0(U))$
is $F(\alpha ^U,\,u^U)=\ell ^1(G,\,C_0(U))$![]() , and hence the ideal generated by $C_0(U)$
, and hence the ideal generated by $C_0(U)$![]() in $F_{\mathcal {R}}(\alpha,\,u)$
in $F_{\mathcal {R}}(\alpha,\,u)$![]() is $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$
is $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$![]() . Moreover, $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)\cap C_0(X)=C_0(U)$
. Moreover, $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)\cap C_0(X)=C_0(U)$![]() . Indeed, the inclusion $C_0(U)\subseteq F_{\mathcal {R}^U}(\alpha ^U,\,u^U)\cap C_0(X)$
. Indeed, the inclusion $C_0(U)\subseteq F_{\mathcal {R}^U}(\alpha ^U,\,u^U)\cap C_0(X)$![]() is obvious and for the opposite inclusion note that $E_1^{\mathcal {R}}$
is obvious and for the opposite inclusion note that $E_1^{\mathcal {R}}$![]() is the identity on $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)\cap C_0(X)$
is the identity on $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)\cap C_0(X)$![]() , and $E_1^{\mathcal {R}}(F_{\mathcal {R}^U}(\alpha ^U,\,u^U))=C_0(U)$
, and $E_1^{\mathcal {R}}(F_{\mathcal {R}^U}(\alpha ^U,\,u^U))=C_0(U)$![]() because $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$
because $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$![]() is the closure of $F(\alpha ^U,\,u^U)$
is the closure of $F(\alpha ^U,\,u^U)$![]() and $E_1(F(\alpha ^U,\,u^U))=C_0(U)$
and $E_1(F(\alpha ^U,\,u^U))=C_0(U)$![]() . This proves the first part of the assertion. For the second part, assume that $C_0(U)$
. This proves the first part of the assertion. For the second part, assume that $C_0(U)$![]() does not detect ideals in $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$
does not detect ideals in $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$![]() , so that there is a non-zero ideal $I$
, so that there is a non-zero ideal $I$![]() in $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$
in $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$![]() with $I\cap C_0(U)=\{0\}$
with $I\cap C_0(U)=\{0\}$![]() . Since $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$
. Since $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$![]() has an approximate unit which is an approximate unit in $C_0(U)$
has an approximate unit which is an approximate unit in $C_0(U)$![]() , and $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$
, and $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$![]() is an ideal in $F_{\mathcal {R}}(\alpha,\,u)$
is an ideal in $F_{\mathcal {R}}(\alpha,\,u)$![]() , we conclude that $I$
, we conclude that $I$![]() is an ideal in $F_{\mathcal {R}}(\alpha,\,u)$
is an ideal in $F_{\mathcal {R}}(\alpha,\,u)$![]() and $I\cap C_0(X)=I\cap C_0(U)=\{0\}$
and $I\cap C_0(X)=I\cap C_0(U)=\{0\}$![]() . Hence, $C_0(X)$
. Hence, $C_0(X)$![]() does not detect ideals in $F_{\mathcal {R}}(\alpha,\,u)$
does not detect ideals in $F_{\mathcal {R}}(\alpha,\,u)$![]() .
.
Lemma 5.15 Suppose that $\varphi$![]() acts by identities, that is $\varphi _g=\text {id}_X$
acts by identities, that is $\varphi _g=\text {id}_X$![]() for $g\in G$
for $g\in G$![]() . For any non-empty $P\subseteq [1,\,\infty ]$
. For any non-empty $P\subseteq [1,\,\infty ]$![]() , $F^P(\alpha,\,u)$
, $F^P(\alpha,\,u)$![]() is isometrically isomorphic to the algebra of $C_0$
is isometrically isomorphic to the algebra of $C_0$![]() -sections of a bundle $\mathcal {B}=\{ F_{\operatorname {r}}^P(G,\,u_x)\}_{x\in X}$
-sections of a bundle $\mathcal {B}=\{ F_{\operatorname {r}}^P(G,\,u_x)\}_{x\in X}$![]() of twisted group reduced Banach algebras, where $u_x(s,\,t):=u(s,\,t)(x)$
of twisted group reduced Banach algebras, where $u_x(s,\,t):=u(s,\,t)(x)$![]() and the isomorphism sends $b\mapsto \widehat {b}$
and the isomorphism sends $b\mapsto \widehat {b}$![]() where $\widehat {b}(x)(t):=b(x,\,t)$
where $\widehat {b}(x)(t):=b(x,\,t)$![]() , $x\in X$
, $x\in X$![]() , $t\in G$
, $t\in G$![]() .
.
Proof. Since $\alpha _{t}=\text {id}$![]() for all $t\in G$
for all $t\in G$![]() , each $u_x \in Z^2(G,\,\mathbb {T})$
, each $u_x \in Z^2(G,\,\mathbb {T})$![]() , $x\in X$
, $x\in X$![]() , is a 2-cocycle for $G$
, is a 2-cocycle for $G$![]() . Since $\varphi$
. Since $\varphi$![]() is trivial we have $\|\cdot \|_{L^1,\operatorname {r}}=\|\cdot \|_{L^{\infty },\,\operatorname {r}}$
is trivial we have $\|\cdot \|_{L^1,\operatorname {r}}=\|\cdot \|_{L^{\infty },\,\operatorname {r}}$![]() by (2.4). Hence, we may assume that $P\subseteq [1,\,\infty )$
by (2.4). Hence, we may assume that $P\subseteq [1,\,\infty )$![]() . A simple calculation shows that for any $b\in F(\alpha,\,u)$
. A simple calculation shows that for any $b\in F(\alpha,\,u)$![]() and $p\in [1,\,\infty )$
and $p\in [1,\,\infty )$![]() we have
we have

This calculation also shows that $\|\widehat {b}(x)\|_{F_{\operatorname {r}}^p(G,\,u_x)}=( \sum _{t\in G}|b(t)(x)|^{p})^{{1}/{p}}$![]() , for each $x\in X$
, for each $x\in X$![]() . This implies that the map $b\mapsto \widehat {b}$
. This implies that the map $b\mapsto \widehat {b}$![]() is a well-defined isometry from $F(\alpha,\,u)\subseteq F^P(\alpha,\,u)$
is a well-defined isometry from $F(\alpha,\,u)\subseteq F^P(\alpha,\,u)$![]() into the space of bounded sections of $\mathcal {B}=\{ F_{\operatorname {r}}^P(G,\,u_x)\}_{x\in X}$
into the space of bounded sections of $\mathcal {B}=\{ F_{\operatorname {r}}^P(G,\,u_x)\}_{x\in X}$![]() equipped with the supremum norm, as we have
equipped with the supremum norm, as we have

Clearly, $b\mapsto \widehat {b}$![]() is an algebra homomorphism. By Fell's reconstruction theorem [Reference Fell and Doran18, II.13.18] there is a unique topology on $\mathcal {B}$
is an algebra homomorphism. By Fell's reconstruction theorem [Reference Fell and Doran18, II.13.18] there is a unique topology on $\mathcal {B}$![]() making sections $\widehat {b}$
making sections $\widehat {b}$![]() , $b\in F(\alpha,\,u)$
, $b\in F(\alpha,\,u)$![]() , continuous. Since elements of $C_c(G,\,C_c(X))\subseteq F(\alpha,\,u)$
, continuous. Since elements of $C_c(G,\,C_c(X))\subseteq F(\alpha,\,u)$![]() are mapped into compactly supported sections of $\mathcal {B}$
are mapped into compactly supported sections of $\mathcal {B}$![]() , and any compactly supported section can be approximated by such elements, we conclude that $b\mapsto \widehat {b}$
, and any compactly supported section can be approximated by such elements, we conclude that $b\mapsto \widehat {b}$![]() extends to the isometric isomorphism $F^P(\alpha,\,u)\cong C_0(\mathcal {B})$
extends to the isometric isomorphism $F^P(\alpha,\,u)\cong C_0(\mathcal {B})$![]() .
.
Proof of theorem 5.12 By corollary 5.8, and as topological freeness passes to subgroups, (1) implies each of the conditions (2)–(4), see also corollary 4.9. Implication (3)$\Rightarrow$![]() (4) is trivial, and (2) implies (4) because cyclic groups are amenable and then the full and reduced crossed products coincide. Thus, it suffices to prove (4)$\Rightarrow$
(4) is trivial, and (2) implies (4) because cyclic groups are amenable and then the full and reduced crossed products coincide. Thus, it suffices to prove (4)$\Rightarrow$![]() (1). To this end, assume $\varphi$
(1). To this end, assume $\varphi$![]() is not topologically free, so that there are $t\in G\setminus \{1\}$
is not topologically free, so that there are $t\in G\setminus \{1\}$![]() and an open non-empty set $U\subseteq X$
and an open non-empty set $U\subseteq X$![]() such that $\varphi _t|_{U}=\text {id}_{U}$
such that $\varphi _t|_{U}=\text {id}_{U}$![]() . Let $H$
. Let $H$![]() be the cyclic group generated by $t$
be the cyclic group generated by $t$![]() . Note that $F_{\operatorname {r}}^P (\alpha |_{H},\,u|_{H})=F^P(\alpha |_{H},\,u|_{H})$
. Note that $F_{\operatorname {r}}^P (\alpha |_{H},\,u|_{H})=F^P(\alpha |_{H},\,u|_{H})$![]() because $H$
because $H$![]() is amenable. If $H\cong \mathbb {Z}$
is amenable. If $H\cong \mathbb {Z}$![]() , then $F(\alpha |_{H},\,u|_{H})\cong F(\alpha |_{H})$
, then $F(\alpha |_{H},\,u|_{H})\cong F(\alpha |_{H})$![]() , and therefore also $F^P(\alpha |_{H},\,u|_{H})\cong F^P(\alpha |_{H})$
, and therefore also $F^P(\alpha |_{H},\,u|_{H})\cong F^P(\alpha |_{H})$![]() , by corollary 2.4. Thus, in this case $C_0(X)$
, by corollary 2.4. Thus, in this case $C_0(X)$![]() does not detect ideals in $F_{\operatorname {r}}^P (\alpha |_{H},\,u|_{H})=F^P(\alpha |_{H},\,u|_{H})$
does not detect ideals in $F_{\operatorname {r}}^P (\alpha |_{H},\,u|_{H})=F^P(\alpha |_{H},\,u|_{H})$![]() by theorem 5.9. Hence, we may assume that $|H|<\infty$
by theorem 5.9. Hence, we may assume that $|H|<\infty$![]() . By passing to a power of $t$
. By passing to a power of $t$![]() we may assume that $|H|$
we may assume that $|H|$![]() is not a square number (or even that it is a prime number). As we want to show that $C_0(X)$
is not a square number (or even that it is a prime number). As we want to show that $C_0(X)$![]() does not detect ideals in $F_{\operatorname {r}}^P (\alpha |_{H},\,u|_{H})$
does not detect ideals in $F_{\operatorname {r}}^P (\alpha |_{H},\,u|_{H})$![]() , by lemma 5.14 we may assume that $U=X$
, by lemma 5.14 we may assume that $U=X$![]() . Assume also that $P$
. Assume also that $P$![]() is non-empty. Then by lemma 5.15 we may identify $F_{\operatorname {r}}^P (\alpha |_{H},\,u|_{H})$
is non-empty. Then by lemma 5.15 we may identify $F_{\operatorname {r}}^P (\alpha |_{H},\,u|_{H})$![]() with $C_0(\{ F_{\operatorname {r}}^P(H,\,u_x)\}_{x\in X})$
with $C_0(\{ F_{\operatorname {r}}^P(H,\,u_x)\}_{x\in X})$![]() . Pick any $x_0\in X$
. Pick any $x_0\in X$![]() . Since $\dim (F_{\operatorname {r}}^P(H,\,u_{x_0}))=|H|$
. Since $\dim (F_{\operatorname {r}}^P(H,\,u_{x_0}))=|H|$![]() is square free, $F_{\operatorname {r}}^P(H,\,u_{x_0})$
is square free, $F_{\operatorname {r}}^P(H,\,u_{x_0})$![]() is not simple. Pick any non-trivial ideal $I_{x_0}$
is not simple. Pick any non-trivial ideal $I_{x_0}$![]() in $F_{\operatorname {r}}^P(H,\,u_{x_0})$
in $F_{\operatorname {r}}^P(H,\,u_{x_0})$![]() . Then
. Then
is a non-trivial ideal in $C_0(\{ F_{\operatorname {r}}^P(H,\,u_x)\}_{x\in X})$![]() . It has zero intersection with $C_0(X)$
. It has zero intersection with $C_0(X)$![]() , which we identify with sections $a\in C_0(\{ F_{\operatorname {r}}^P(H,\,u_x)\}_{x\in X})$
, which we identify with sections $a\in C_0(\{ F_{\operatorname {r}}^P(H,\,u_x)\}_{x\in X})$![]() such that $a(x)\in \mathbb {C} \cdot 1_{x}$
such that $a(x)\in \mathbb {C} \cdot 1_{x}$![]() where $1_{x}$
where $1_{x}$![]() is the identity in $F_{\operatorname {r}}^P(H,\,u_{x_0})$
is the identity in $F_{\operatorname {r}}^P(H,\,u_{x_0})$![]() . Hence, $C_0(X)$
. Hence, $C_0(X)$![]() does not detect ideals in $F_{\operatorname {r}}^P (\alpha |_{H},\,u|_{H})$
does not detect ideals in $F_{\operatorname {r}}^P (\alpha |_{H},\,u|_{H})$![]() . This also gives the claim about $F^{\emptyset }(\alpha |_{H},\,u|_{H})=F(\alpha |_{H},\,u|_{H})$
. This also gives the claim about $F^{\emptyset }(\alpha |_{H},\,u|_{H})=F(\alpha |_{H},\,u|_{H})$![]() by the last part of remark 4.3 because $H$
by the last part of remark 4.3 because $H$![]() is finite.
is finite.
6. Simplicity and ideal structure
The previous results give immediately the following simplicity criteria. Recall that $\varphi$![]() is an action of a discrete group $G$
is an action of a discrete group $G$![]() on a locally compact Hausdorff space $X$
on a locally compact Hausdorff space $X$![]() , and $\alpha$
, and $\alpha$![]() is the corresponding action on the commutative $C^*$
is the corresponding action on the commutative $C^*$![]() -algebra $C_0(X)$
-algebra $C_0(X)$![]() .
.
Definition 6.1 We say $\varphi$![]() is minimal if there are no non-trivial open $\varphi$
is minimal if there are no non-trivial open $\varphi$![]() -invariant sets in $X$
-invariant sets in $X$![]() . In general, we denote by $\mathcal {I}^\varphi (X)$
. In general, we denote by $\mathcal {I}^\varphi (X)$![]() the lattice of all open $\varphi$
the lattice of all open $\varphi$![]() -invariant sets in $X$
-invariant sets in $X$![]() .
.
Lemma 6.2 Let $F_{\mathcal {R}}(\alpha,\,u)$![]() be a twisted crossed product admitting the Fourier decomposition $\{E_t^{\mathcal {R}}\}_{t\in G}$
be a twisted crossed product admitting the Fourier decomposition $\{E_t^{\mathcal {R}}\}_{t\in G}$![]() . All non-trivial ideals in $F_{\mathcal {R}}(\alpha,\,u)$
. All non-trivial ideals in $F_{\mathcal {R}}(\alpha,\,u)$![]() are contained in $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$
are contained in $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$![]() if and only if $\varphi$
if and only if $\varphi$![]() is minimal and $C_0(X)\subseteq F_{\mathcal {R}}(\alpha,\,u)$
is minimal and $C_0(X)\subseteq F_{\mathcal {R}}(\alpha,\,u)$![]() has the generalized intersection property with $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$
has the generalized intersection property with $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$![]() as the hidden ideal. In particular, $F_{\mathcal {R}}(\alpha,\,u)$
as the hidden ideal. In particular, $F_{\mathcal {R}}(\alpha,\,u)$![]() is simple if and only if it is reduced, $C_0(X)$
is simple if and only if it is reduced, $C_0(X)$![]() detects ideals in $F_{\mathcal {R}}(\alpha,\,u)$
detects ideals in $F_{\mathcal {R}}(\alpha,\,u)$![]() and $\varphi$
and $\varphi$![]() is minimal.
is minimal.
Proof. If all non-trivial ideals in $F_{\mathcal {R}}(\alpha,\,u)$![]() are contained in $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$
are contained in $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$![]() , then $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$
, then $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$![]() is the hidden ideal for $C_0(X)\subseteq F_{\mathcal {R}}(\alpha,\,u)$
is the hidden ideal for $C_0(X)\subseteq F_{\mathcal {R}}(\alpha,\,u)$![]() , and $\varphi$
, and $\varphi$![]() is minimal by lemma 5.14. Conversely, assume $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$
is minimal by lemma 5.14. Conversely, assume $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$![]() is the hidden ideal for $C_0(X)\subseteq F_{\mathcal {R}}(\alpha,\,u)$
is the hidden ideal for $C_0(X)\subseteq F_{\mathcal {R}}(\alpha,\,u)$![]() and let $J$
and let $J$![]() be an ideal in $F_{\mathcal {R}}(\alpha,\,u)$
be an ideal in $F_{\mathcal {R}}(\alpha,\,u)$![]() which is not contained in $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$
which is not contained in $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$![]() . Then $J$
. Then $J$![]() intersects $C_0(X)$
intersects $C_0(X)$![]() non-trivially and hence, by lemma 5.14, $J$
non-trivially and hence, by lemma 5.14, $J$![]() contains $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$
contains $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$![]() for some non-empty $\varphi$
for some non-empty $\varphi$![]() -invariant open $U\subseteq X$
-invariant open $U\subseteq X$![]() . Thus, if $\varphi$
. Thus, if $\varphi$![]() is minimal, we necessarily have $J=F_{\mathcal {R}}(\alpha,\,u)$
is minimal, we necessarily have $J=F_{\mathcal {R}}(\alpha,\,u)$![]() , that is $J$
, that is $J$![]() is trivial.
is trivial.
Theorem 6.3 Simplicity
Let $\alpha$![]() be an action of a discrete group $G$
be an action of a discrete group $G$![]() on $C_0(X)$
on $C_0(X)$![]() . The following conditions are equivalent:
. The following conditions are equivalent:
(1) The dual map $\varphi$
 is topologically free and minimal.
is topologically free and minimal.(2) All reduced twisted crossed products $F_{\mathcal {R}}(\alpha,\,u)$
 , $u\in Z^2(G,\, C_u(X))$
, $u\in Z^2(G,\, C_u(X))$ , are simple.
, are simple.(3) $F^P(\alpha )$
 is simple for some (and hence all) $P\subseteq \{1,\,\infty \}$
is simple for some (and hence all) $P\subseteq \{1,\,\infty \}$ .
.(4) For any twisted crossed product $F_{\mathcal {R}}(\alpha,\,u)$
 , $u\in Z^2(G,\, C_u(X))$
, $u\in Z^2(G,\, C_u(X))$ , admitting the Fourier decomposition $\{E_t^{\mathcal {R}}\}_{t\in G}$
, admitting the Fourier decomposition $\{E_t^{\mathcal {R}}\}_{t\in G}$ all non-trivial ideals in $F_{\mathcal {R}}(\alpha,\,u)$
all non-trivial ideals in $F_{\mathcal {R}}(\alpha,\,u)$ are contained in $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$
are contained in $\bigcap _{t\in G}\ker (E_t^{\mathcal {R}})$ .
.(5) All non-trivial ideals in $F^P(\alpha )$
 are contained in $\ker (\Lambda _P)$
are contained in $\ker (\Lambda _P)$ for some (and hence all) $P\subseteq [1,\,\infty ]$
for some (and hence all) $P\subseteq [1,\,\infty ]$ .
.
In particular, for any $P\subseteq [1,\,\infty ]$![]() , the full crossed product $F^P(\alpha )$
, the full crossed product $F^P(\alpha )$![]() is simple if and only if the regular representation $\Lambda _P$
is simple if and only if the regular representation $\Lambda _P$![]() is injective and $\varphi$
is injective and $\varphi$![]() is topologically free and minimal.
is topologically free and minimal.
Proof. (1) implies (2) and (4) by lemma 6.2 and corollary 5.8. Implications (2)$\Rightarrow$![]() (3) and (4)$\Rightarrow$
(3) and (4)$\Rightarrow$![]() (5) are immediate, see remark 4.13 and corollary 4.14. We have (3)$\Rightarrow$
(5) are immediate, see remark 4.13 and corollary 4.14. We have (3)$\Rightarrow$![]() (1) and (5)$\Rightarrow$
(1) and (5)$\Rightarrow$![]() (1) by lemma 6.2 and theorem 5.9. This proves the equivalence of conditions (1)–(5). The final claim now follows from the equivalence (1)$\Leftrightarrow$
(1) by lemma 6.2 and theorem 5.9. This proves the equivalence of conditions (1)–(5). The final claim now follows from the equivalence (1)$\Leftrightarrow$![]() (5).
(5).
In order to apply our results to non-minimal actions, let us first consider a general inclusion $A\subseteq B$![]() of Banach algebras. Let $\mathcal {I}(A)$
of Banach algebras. Let $\mathcal {I}(A)$![]() be the set of all (closed, two-sided) ideals in $A$
be the set of all (closed, two-sided) ideals in $A$![]() , equipped with the partial order given by inclusion. This makes $\mathcal {I}(A)$
, equipped with the partial order given by inclusion. This makes $\mathcal {I}(A)$![]() a complete lattice: for a family of ideals $\{I_{s}\}_{s\in S} \subseteq \mathcal {I}(A)$
a complete lattice: for a family of ideals $\{I_{s}\}_{s\in S} \subseteq \mathcal {I}(A)$![]() , their join in $\mathcal {I}(A)$
, their join in $\mathcal {I}(A)$![]() is the closed linear span $\operatorname {\overline {span}}\{a: a\in I_s,\, s\in S\}$
is the closed linear span $\operatorname {\overline {span}}\{a: a\in I_s,\, s\in S\}$![]() , and their meet in $\mathcal {I}(A)$
, and their meet in $\mathcal {I}(A)$![]() is the intersection $\bigcap _{s\in S} I_s$
is the intersection $\bigcap _{s\in S} I_s$![]() .
.
Definition 6.4 Let $A$![]() be a Banach subalgebra of a Banach algebra $B$
be a Banach subalgebra of a Banach algebra $B$![]() . We define maps $\operatorname {Res}:\mathcal {I}(B)\to \mathcal {I}(A)$
. We define maps $\operatorname {Res}:\mathcal {I}(B)\to \mathcal {I}(A)$![]() and $\operatorname {Ex}:\mathcal {I}(A)\to \mathcal {I}(B)$
and $\operatorname {Ex}:\mathcal {I}(A)\to \mathcal {I}(B)$![]() where, for $J\in \mathcal {I}(B)$
where, for $J\in \mathcal {I}(B)$![]() , $I\in \mathcal {I}(A)$
, $I\in \mathcal {I}(A)$![]() ,
,
(if $B$![]() has an approximate unit, then $\operatorname {Ex}(I)=\overline {BIB}$
has an approximate unit, then $\operatorname {Ex}(I)=\overline {BIB}$![]() ). We call elements of $\operatorname {Res}(\mathcal {I}(B))\subseteq \mathcal {I}(A)$
). We call elements of $\operatorname {Res}(\mathcal {I}(B))\subseteq \mathcal {I}(A)$![]() restricted ideals and elements of $\operatorname {Ex}(\mathcal {I}(A))\subseteq \mathcal {I}(B)$
restricted ideals and elements of $\operatorname {Ex}(\mathcal {I}(A))\subseteq \mathcal {I}(B)$![]() extended ideals for the inclusion $A\subseteq B$
extended ideals for the inclusion $A\subseteq B$![]() .
.
Clearly, the maps $\operatorname {Res}$![]() and $\operatorname {Ex}$
and $\operatorname {Ex}$![]() preserve inclusions and for any $I\in \mathcal {I}(A)$
preserve inclusions and for any $I\in \mathcal {I}(A)$![]() , $J\in \mathcal {I}(B)$
, $J\in \mathcal {I}(B)$![]() we have
we have
Thus, $\operatorname {Res}$![]() and $\operatorname {Ex}$
and $\operatorname {Ex}$![]() form a monotone Galois connection (they are contravariantly adjoint maps) between the lattices $\mathcal {I}(A)$
form a monotone Galois connection (they are contravariantly adjoint maps) between the lattices $\mathcal {I}(A)$![]() and $\mathcal {I}(B)$
and $\mathcal {I}(B)$![]() . For $C^*$
. For $C^*$![]() -algebras this was noticed already by Green, see [Reference Green24, Proposition 9.(i)], and has a number of useful consequences. For instance, $\operatorname {Ex}$
-algebras this was noticed already by Green, see [Reference Green24, Proposition 9.(i)], and has a number of useful consequences. For instance, $\operatorname {Ex}$![]() and $\operatorname {Res}$
and $\operatorname {Res}$![]() give an isomorphism $\operatorname {Res}(\mathcal {I}(B))\cong \operatorname {Ex}(\mathcal {I}(A))$
give an isomorphism $\operatorname {Res}(\mathcal {I}(B))\cong \operatorname {Ex}(\mathcal {I}(A))$![]() and these sets with an inclusion as a preorder are complete lattices, cf. [Reference Kwaśniewski and Meyer29, Proposition 2.9].
and these sets with an inclusion as a preorder are complete lattices, cf. [Reference Kwaśniewski and Meyer29, Proposition 2.9].
Definition 6.5 cf. [Reference Kwaśniewski and Meyer29, Definition 2.11]
We say that $A$![]() separates ideals in $B$
separates ideals in $B$![]() if for every two different $J_1,\, J_2\in \mathcal {I}(B)$
if for every two different $J_1,\, J_2\in \mathcal {I}(B)$![]() we have $J_1\cap A \neq J_2\cap A$
we have $J_1\cap A \neq J_2\cap A$![]() .
.
Lemma 6.6 cf. [Reference Kwaśniewski and Meyer29, Proposition 2.12]
Let $A\subseteq B$![]() be an inclusion of Banach algebras. The following conditions are equivalent:
be an inclusion of Banach algebras. The following conditions are equivalent:
(1) $A$
 separates ideals in $B$
separates ideals in $B$ (the map $\operatorname {Res}$
(the map $\operatorname {Res}$ is injective).
is injective).(2) Every ideal in $B$
 is extended from $A$
is extended from $A$ (the map $\operatorname {Ex}$
(the map $\operatorname {Ex}$ is surjective).
is surjective).(3) $\mathcal {I}(B)\cong \operatorname {Res}(\mathcal {I}(B))\subseteq \mathcal {I}(A)$
 with the isomorphism given by $\operatorname {Res}$
with the isomorphism given by $\operatorname {Res}$ .
.
If $A$![]() is a $C^*$
is a $C^*$![]() -algebra, then for every $I\in \operatorname {Res}(\mathcal {I}(B))$
-algebra, then for every $I\in \operatorname {Res}(\mathcal {I}(B))$![]() , the image of $A$
, the image of $A$![]() in the quotient $B/\operatorname {Ex}(I)$
in the quotient $B/\operatorname {Ex}(I)$![]() is naturally isometrically isomorphic to $A/I$
is naturally isometrically isomorphic to $A/I$![]() and each of the above conditions is equivalent to
and each of the above conditions is equivalent to
(4) $A$
 ‘residually detects ideals’ in $B$
‘residually detects ideals’ in $B$ , that is, $A/I$
, that is, $A/I$ detects ideals in the quotient $B/\operatorname {Ex}(I)$
detects ideals in the quotient $B/\operatorname {Ex}(I)$ for every $I\in \operatorname {Res}(\mathcal {I}(B))$
for every $I\in \operatorname {Res}(\mathcal {I}(B))$ .
.
Proof. Equivalences between (1) and (3) hold for any Galois connection (in particular $\operatorname {Res}$![]() and $\operatorname {Ex}$
and $\operatorname {Ex}$![]() are generalized inverses of each other). Assume now that $A$
are generalized inverses of each other). Assume now that $A$![]() is a $C^*$
is a $C^*$![]() -algebra. Let $I\in \operatorname {Res}(\mathcal {I}(B))$
-algebra. Let $I\in \operatorname {Res}(\mathcal {I}(B))$![]() . Then $A\cap \operatorname {Ex}(I)=\operatorname {Res}(\operatorname {Ex}(I))=I$
. Then $A\cap \operatorname {Ex}(I)=\operatorname {Res}(\operatorname {Ex}(I))=I$![]() and hence the map $A/I\ni a +I \mapsto a+\operatorname {Ex}(I)\in B/\operatorname {Ex}(I)$
and hence the map $A/I\ni a +I \mapsto a+\operatorname {Ex}(I)\in B/\operatorname {Ex}(I)$![]() is an injective representation. By minimality of the $C^*$
is an injective representation. By minimality of the $C^*$![]() -norm, see lemma 5.4, this representation is in fact isometric. Now assume that (2) fails. Then there is $J\in \mathcal {I}(B)$
-norm, see lemma 5.4, this representation is in fact isometric. Now assume that (2) fails. Then there is $J\in \mathcal {I}(B)$![]() with $J\neq \operatorname {Ex}(I)$
with $J\neq \operatorname {Ex}(I)$![]() where $I:=J\cap A\in \operatorname {Res}(\mathcal {I}(B))$
where $I:=J\cap A\in \operatorname {Res}(\mathcal {I}(B))$![]() . Since $\operatorname {Ex}(I)\subsetneq J$
. Since $\operatorname {Ex}(I)\subsetneq J$![]() , the image of $J$
, the image of $J$![]() in $B/\operatorname {Ex}(I)$
in $B/\operatorname {Ex}(I)$![]() is a non-zero ideal that can be identified with the quotient $J/\operatorname {Ex}(I)$
is a non-zero ideal that can be identified with the quotient $J/\operatorname {Ex}(I)$![]() (and so in particular this image is closed), and whose intersection with $A/I$
(and so in particular this image is closed), and whose intersection with $A/I$![]() is zero. Thus, $A/I$
is zero. Thus, $A/I$![]() does not detect ideals in $B/\operatorname {Ex}(I)$
does not detect ideals in $B/\operatorname {Ex}(I)$![]() , and hence (4) fails. Conversely, assume that $A/I$
, and hence (4) fails. Conversely, assume that $A/I$![]() does not detect ideals in $B/\operatorname {Ex}(I)$
does not detect ideals in $B/\operatorname {Ex}(I)$![]() for some $I\in \operatorname {Res}(\mathcal {I}(B))$
for some $I\in \operatorname {Res}(\mathcal {I}(B))$![]() , so there is a non-zero ideal $K\subseteq B/\operatorname {Ex}(I)$
, so there is a non-zero ideal $K\subseteq B/\operatorname {Ex}(I)$![]() whose intersection with $A/I$
whose intersection with $A/I$![]() is zero. The preimage of $K$
is zero. The preimage of $K$![]() under the quotient map is an ideal $J\in \mathcal {I}(B)$
under the quotient map is an ideal $J\in \mathcal {I}(B)$![]() such that $J\cap A=I$
such that $J\cap A=I$![]() , but $\operatorname {Ex}(I)\subsetneq J$
, but $\operatorname {Ex}(I)\subsetneq J$![]() , and hence (2) fails.
, and hence (2) fails.
Let us now consider the case when $A=C_0(X)$![]() and $B=F_{\mathcal {R}}(\alpha,\,u)$
and $B=F_{\mathcal {R}}(\alpha,\,u)$![]() is a Banach algebra crossed product. It follows from lemma 5.14 that $\operatorname {Res}(\mathcal {I}(B))$
is a Banach algebra crossed product. It follows from lemma 5.14 that $\operatorname {Res}(\mathcal {I}(B))$![]() can be identified with the lattice $\mathcal {I}^\varphi (X)$
can be identified with the lattice $\mathcal {I}^\varphi (X)$![]() of all open $\varphi$
of all open $\varphi$![]() -invariant sets in $X$
-invariant sets in $X$![]() . It also implies that $J\in \operatorname {Ex}(\mathcal {I}(A))$
. It also implies that $J\in \operatorname {Ex}(\mathcal {I}(A))$![]() if and only if $J=F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$
if and only if $J=F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$![]() for some $U\in \mathcal {I}^\varphi (X)$
for some $U\in \mathcal {I}^\varphi (X)$![]() . Thus, in view of lemma 6.6 (see statement (4)), for separation of ideals in $F_{\mathcal {R}}(\alpha,\,u)$
. Thus, in view of lemma 6.6 (see statement (4)), for separation of ideals in $F_{\mathcal {R}}(\alpha,\,u)$![]() we need the following property, which in the $C^*$
we need the following property, which in the $C^*$![]() -algebraic considerations is called exactness, see [Reference Sierakowski40, Definition 1.5] (as it can be used to characterize exactness of the group, see [Reference Brown and Ozawa9, Theorem 5.1.10]). We find the name residually reduced more appropriate in our more general context.
-algebraic considerations is called exactness, see [Reference Sierakowski40, Definition 1.5] (as it can be used to characterize exactness of the group, see [Reference Brown and Ozawa9, Theorem 5.1.10]). We find the name residually reduced more appropriate in our more general context.
Definition 6.7 A crossed product $F_{\mathcal {R}}(\alpha,\,u)$![]() is residually reduced if for every $U\in \mathcal {I}^\varphi (X)$
is residually reduced if for every $U\in \mathcal {I}^\varphi (X)$![]() the quotient Banach algebra $F_{\mathcal {R}}(\alpha,\,u)/F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$
the quotient Banach algebra $F_{\mathcal {R}}(\alpha,\,u)/F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$![]() is naturally a reduced crossed product for $(\alpha ^Y,\,u^Y)$
is naturally a reduced crossed product for $(\alpha ^Y,\,u^Y)$![]() where $Y=X\setminus U$
where $Y=X\setminus U$![]() .
.
Remark 6.8 If $F_{\mathcal {R}}(\alpha,\,u)$![]() is residually reduced, then it is reduced (consider $U=\emptyset$
is residually reduced, then it is reduced (consider $U=\emptyset$![]() ). When $\varphi$
). When $\varphi$![]() is minimal the converse implication holds trivially (as then $\mathcal {I}^\varphi (X)=\{\emptyset,\, X\}$
is minimal the converse implication holds trivially (as then $\mathcal {I}^\varphi (X)=\{\emptyset,\, X\}$![]() ).
).
Lemma 6.9 $F_{\mathcal {R}}(\alpha,\,u)$![]() is a residually reduced crossed product if and only if $F_{\mathcal {R}}(\alpha,\,u)$
is a residually reduced crossed product if and only if $F_{\mathcal {R}}(\alpha,\,u)$![]() admits the Fourier decomposition $\{E_t^{\mathcal {R}}\}_{t\in G}$
admits the Fourier decomposition $\{E_t^{\mathcal {R}}\}_{t\in G}$![]() and for any open $\varphi$
and for any open $\varphi$![]() -invariant subset $U\subseteq X$
-invariant subset $U\subseteq X$![]() we have
we have
Proof. If $F_{\mathcal {R}}(\alpha,\,u)$![]() is a reduced crossed product it admits the FD. Assume then that $F_{\mathcal {R}}(\alpha,\,u)$
is a reduced crossed product it admits the FD. Assume then that $F_{\mathcal {R}}(\alpha,\,u)$![]() admits the FD and let $U\in \mathcal {I}^\varphi (X)$
admits the FD and let $U\in \mathcal {I}^\varphi (X)$![]() . The maps $\{E_t^{\mathcal {R}}\}_{t\in G}$
. The maps $\{E_t^{\mathcal {R}}\}_{t\in G}$![]() descend to contractive linear maps $E_t^{\mathcal {R}^Y}:F_{\mathcal {R}}(\alpha,\,u)/F_{\mathcal {R}^U}(\alpha ^U,\,u^U)\to C_0(X)/C_0(U)\cong C_0(Y)$
descend to contractive linear maps $E_t^{\mathcal {R}^Y}:F_{\mathcal {R}}(\alpha,\,u)/F_{\mathcal {R}^U}(\alpha ^U,\,u^U)\to C_0(X)/C_0(U)\cong C_0(Y)$![]() ;
;
These maps form the FD for $F_{\mathcal {R}}(\alpha,\,u)/F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$![]() viewed as the completion of $F(\alpha ^Y,\,u^Y)$
viewed as the completion of $F(\alpha ^Y,\,u^Y)$![]() . This quotient crossed product is reduced if and only if $\bigcap _{t\in G} E_t^{\mathcal {R}^Y}=\{0\}$
. This quotient crossed product is reduced if and only if $\bigcap _{t\in G} E_t^{\mathcal {R}^Y}=\{0\}$![]() , which holds if and only if $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)=\{b\in F_{\mathcal {R}}(\alpha,\,u): E_t^{\mathcal {R}}(b)\in C_0(U) \text { for all }t\in G\}$
, which holds if and only if $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)=\{b\in F_{\mathcal {R}}(\alpha,\,u): E_t^{\mathcal {R}}(b)\in C_0(U) \text { for all }t\in G\}$![]() .
.
Proposition 6.10 For any $P\subseteq \{1,\,\infty \}$![]() the crossed product $F^P(\alpha,\,u)$
the crossed product $F^P(\alpha,\,u)$![]() is always residually reduced. More specifically, for $U\in \mathcal {I}^\varphi (X)$
is always residually reduced. More specifically, for $U\in \mathcal {I}^\varphi (X)$![]() and $Y:=X\setminus U$
and $Y:=X\setminus U$![]() the restriction map $\ell ^{1}(G,\,C_0(X))\ni b\mapsto b|_{Y}\in \ell ^{1}(G,\,C_0(Y)) \text { where } b|_{Y}(t):=b(t)|_Y,\,\, t\in G ,\,$
the restriction map $\ell ^{1}(G,\,C_0(X))\ni b\mapsto b|_{Y}\in \ell ^{1}(G,\,C_0(Y)) \text { where } b|_{Y}(t):=b(t)|_Y,\,\, t\in G ,\,$![]() yields an isometric isomorphism
yields an isometric isomorphism
Proof. Let $b \in C_c(G,\, C_0(X))\subseteq F(\alpha,\,u)$![]() . For any $c\in F(\alpha ^U,\,u^U)$
. For any $c\in F(\alpha ^U,\,u^U)$![]() we clearly have inequalities
we clearly have inequalities

The set $G_b=\{t\in G: b(t)\neq 0\}$![]() is finite. For any $\varepsilon >0$
is finite. For any $\varepsilon >0$![]() and any $t\in G_b$
and any $t\in G_b$![]() there is $c(t)\in C_0(U)$
there is $c(t)\in C_0(U)$![]() such that $\max _{x\in U}|b(t)(x)+c(t)(x)|\leq \max _{x\in \partial U}|b(t)(x)|+\varepsilon /|G_b|$
such that $\max _{x\in U}|b(t)(x)+c(t)(x)|\leq \max _{x\in \partial U}|b(t)(x)|+\varepsilon /|G_b|$![]() where $\partial U:=\overline {U}\cap Y$
where $\partial U:=\overline {U}\cap Y$![]() is the common boundary of $U$
is the common boundary of $U$![]() and $Y$
and $Y$![]() . This gives $c\in C_c(G,\, C_0(X)) \subseteq F(\alpha ^U,\,u^U)$
. This gives $c\in C_c(G,\, C_0(X)) \subseteq F(\alpha ^U,\,u^U)$![]() such that
such that
and $\|b+c\|_{F^\infty (\alpha,u)} \leq \|b|_{Y}\|_{F^\infty (\alpha ^Y,u^Y)} +\varepsilon$![]() . This shows that $\inf _{c\in F(\alpha ^U,u^U)} \|b+c\|_{ F(\alpha,u)} = \|b|_{Y}\|_{F(\alpha ^Y,u^Y)}$
. This shows that $\inf _{c\in F(\alpha ^U,u^U)} \|b+c\|_{ F(\alpha,u)} = \|b|_{Y}\|_{F(\alpha ^Y,u^Y)}$![]() and if $P\subseteq \{1,\,\infty \}$
and if $P\subseteq \{1,\,\infty \}$![]() is non-empty, then
is non-empty, then
Hence, the map $b\mapsto b|_{Y}$![]() induces the surjective isometry (6.1), which clearly is linear and multiplicative, and hence it is an isometric isomorphism.
induces the surjective isometry (6.1), which clearly is linear and multiplicative, and hence it is an isometric isomorphism.
Lemma 6.11 Let $F_{\mathcal {R}}(\alpha,\,u)$![]() be a crossed product. The following conditions are equivalent:
be a crossed product. The following conditions are equivalent:
(1) $C_0(X)$
 separates ideals in $F_{\mathcal {R}}(\alpha,\,u)$
separates ideals in $F_{\mathcal {R}}(\alpha,\,u)$ .
.(2) Every ideal in $F_{\mathcal {R}}(\alpha,\,u)$
 is generated by its intersection with $C_0(X)$
is generated by its intersection with $C_0(X)$ .
.(3) We have a lattice isomorphism $\mathcal {I}^{\varphi }(X)\cong \mathcal {I}(F_{\mathcal {R}}(\alpha,\,u))$
 given by $U\mapsto F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$
given by $U\mapsto F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$ .
.(4) $C_0(X\setminus U)$
 detects ideals in $F_{\mathcal {R}}(\alpha,\,u)/F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$
detects ideals in $F_{\mathcal {R}}(\alpha,\,u)/F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$ for every $U\in \mathcal {I}^\varphi (X)$
for every $U\in \mathcal {I}^\varphi (X)$ .
.
If these equivalent conditions hold, then $F_{\mathcal {R}}(\alpha,\,u)$![]() is necessarily residually reduced.
is necessarily residually reduced.
Proof. By lemma 5.14, conditions (1)–(4) are special cases of conditions (1)–(4) in lemma 6.6. Assume that $F_{\mathcal {R}}(\alpha,\,u)$![]() is not residually reduced. Then there is $U\in \mathcal {I}^\varphi (X)$
is not residually reduced. Then there is $U\in \mathcal {I}^\varphi (X)$![]() such that $F_{\mathcal {R}}(\alpha,\,u)/F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$
such that $F_{\mathcal {R}}(\alpha,\,u)/F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$![]() (which is a crossed product for $(\alpha ^{X\setminus U},\,u^{X\setminus U})$
(which is a crossed product for $(\alpha ^{X\setminus U},\,u^{X\setminus U})$![]() that admits the FD, cf. the proof of lemma 6.9) is not reduced. Then $C_0(X\setminus U)$
that admits the FD, cf. the proof of lemma 6.9) is not reduced. Then $C_0(X\setminus U)$![]() does not detect ideals in $F_{\mathcal {R}}(\alpha,\,u)/F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$
does not detect ideals in $F_{\mathcal {R}}(\alpha,\,u)/F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$![]() by remark 5.7. This contradicts (4).
by remark 5.7. This contradicts (4).
Definition 6.12 [Reference Sierakowski40, Remark 1.18]
We say $\varphi$![]() is residually topologically free if for any closed $\varphi$
is residually topologically free if for any closed $\varphi$![]() -invariant subset $Y\subseteq X$
-invariant subset $Y\subseteq X$![]() the restriction $\varphi ^Y:G\to \operatorname {Homeo}(Y)$
the restriction $\varphi ^Y:G\to \operatorname {Homeo}(Y)$![]() , $\varphi ^Y_t:=\varphi _{t}|_{Y}$
, $\varphi ^Y_t:=\varphi _{t}|_{Y}$![]() , is topologically free.
, is topologically free.
Theorem 6.13 Separation of ideals
Let $\alpha$![]() be an action of a discrete group $G$
be an action of a discrete group $G$![]() on $C_0(X)$
on $C_0(X)$![]() . The following conditions are equivalent:
. The following conditions are equivalent:
(1) The dual action $\varphi$
 is residually topologically free.
is residually topologically free.(2) $C_0(X)$
 separates ideals in every residually reduced twisted crossed product $F_{\mathcal {R}}(\alpha,\,u)$
separates ideals in every residually reduced twisted crossed product $F_{\mathcal {R}}(\alpha,\,u)$ , so the map $U\mapsto F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$
, so the map $U\mapsto F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$ is a lattice isomorphism $\mathcal {I}^{\varphi }(X)\cong \mathcal {I}(F_{\mathcal {R}}(\alpha,\,u))$
is a lattice isomorphism $\mathcal {I}^{\varphi }(X)\cong \mathcal {I}(F_{\mathcal {R}}(\alpha,\,u))$ .
.(3) For some (and hence all) $P\subseteq \{1,\,\infty \}$
 the map $U\mapsto F^P(\alpha ^U)$
the map $U\mapsto F^P(\alpha ^U)$ gives $\mathcal {I}^{\varphi }(X)\cong \mathcal {I}(F^P(\alpha ))$
gives $\mathcal {I}^{\varphi }(X)\cong \mathcal {I}(F^P(\alpha ))$ .
.(4) For any twisted crossed product $F_{\mathcal {R}}(\alpha,\,u)$
 , $C_0(X)$
, $C_0(X)$ separates ideals in $F_{\mathcal {R}}(\alpha,\,u)$
separates ideals in $F_{\mathcal {R}}(\alpha,\,u)$ if and only if $F_{\mathcal {R}}(\alpha,\,u)$
if and only if $F_{\mathcal {R}}(\alpha,\,u)$ is residually reduced.
is residually reduced.
Proof. (1) implies (2) by lemma 6.11 and corollary 5.8. Conditions (2) and (5) are equivalent by the last part of lemma 6.11. By proposition 6.10, (2) implies (3). This proposition combined with theorem 5.9 shows that (3) is equivalent to (1).
Remark 6.14 If the action $\varphi$![]() is amenable, its restriction $\varphi ^Y$
is amenable, its restriction $\varphi ^Y$![]() to any closed $\varphi$
to any closed $\varphi$![]() -invariant set $Y\subseteq X$
-invariant set $Y\subseteq X$![]() is also amenable. It is a well-known $C^*$
is also amenable. It is a well-known $C^*$![]() -algebraic fact that for every $U\in \mathcal {I}^\varphi (X)$
-algebraic fact that for every $U\in \mathcal {I}^\varphi (X)$![]() we have a natural isometric $*$
we have a natural isometric $*$![]() -isomorphism $F^2(\alpha,\,u)/F^2(\alpha ^U,\,u^U)\cong F^2(\alpha ^{Y},\,u^{Y})$
-isomorphism $F^2(\alpha,\,u)/F^2(\alpha ^U,\,u^U)\cong F^2(\alpha ^{Y},\,u^{Y})$![]() where $Y:=X\setminus U$
where $Y:=X\setminus U$![]() . Hence, if $\varphi$
. Hence, if $\varphi$![]() is amenable, then $F^2(\alpha,\,u)$
is amenable, then $F^2(\alpha,\,u)$![]() is residually reduced by theorem 3.5. For $p\neq 1,\,2,\,\infty$
is residually reduced by theorem 3.5. For $p\neq 1,\,2,\,\infty$![]() this is not clear, and the problem is that we do not know whether the quotient $F^p(\alpha,\,u)/F^p(\alpha ^U,\,u^U)$
this is not clear, and the problem is that we do not know whether the quotient $F^p(\alpha,\,u)/F^p(\alpha ^U,\,u^U)$![]() is an $L^p$
is an $L^p$![]() -operator algebra. If $G$
-operator algebra. If $G$![]() is finite, then all Banach algebra crossed products $F_{\mathcal {R}}(\alpha,\,u)$
is finite, then all Banach algebra crossed products $F_{\mathcal {R}}(\alpha,\,u)$![]() are residually reduced, as they are all equal as topological algebras, see remark 4.3.
are residually reduced, as they are all equal as topological algebras, see remark 4.3.
Definition 6.15 Let $A$![]() be a Banach algebra. The prime ideal space of $A$
be a Banach algebra. The prime ideal space of $A$![]() is the set $\operatorname {Prime}(A)$
is the set $\operatorname {Prime}(A)$![]() of prime elements in the lattice $\mathcal {I}(A)$
of prime elements in the lattice $\mathcal {I}(A)$![]() of all closed ideals in $A$
of all closed ideals in $A$![]() .
.
Thus $p\in \operatorname {Prime}(A)$![]() if and only if $p\in \mathcal {I}(A)\setminus \{A\}$
if and only if $p\in \mathcal {I}(A)\setminus \{A\}$![]() and for any $I_1,\,I_2\in \mathcal {I}(A)$
and for any $I_1,\,I_2\in \mathcal {I}(A)$![]() , the inclusion $I_1\cap I_2\subseteq p$
, the inclusion $I_1\cap I_2\subseteq p$![]() implies that either $I_1\subseteq p$
implies that either $I_1\subseteq p$![]() or $I_2\subseteq p$
or $I_2\subseteq p$![]() . We equip $\operatorname {Prime}(A)$
. We equip $\operatorname {Prime}(A)$![]() with the topology given by the sets
with the topology given by the sets
Note that the map $\mathcal {I}(A)\ni I\to U_I\subseteq \operatorname {Prime}(A)$![]() maps finite meets into intersections and arbitrary joins to unions. Thus, $\{U_{I}\}_{I\in \mathcal {I}(A)}$
maps finite meets into intersections and arbitrary joins to unions. Thus, $\{U_{I}\}_{I\in \mathcal {I}(A)}$![]() is indeed a topology on $\operatorname {Prime}(A)$
is indeed a topology on $\operatorname {Prime}(A)$![]() .
.
Lemma 6.16 Assume that $A$![]() is a $C^*$
is a $C^*$![]() -algebra whose primitive ideal space $\check {A}$
-algebra whose primitive ideal space $\check {A}$![]() is second countable. Then $\check {A}=\operatorname {Prime}(A)$
is second countable. Then $\check {A}=\operatorname {Prime}(A)$![]() . Let $A\subseteq B$
. Let $A\subseteq B$![]() be an inclusion of Banach algebras which is symmetric in the sense that $\operatorname {Ex}(I)=\overline {IB}$
be an inclusion of Banach algebras which is symmetric in the sense that $\operatorname {Ex}(I)=\overline {IB}$![]() for every $I\in \operatorname {Res}(\mathcal {I}(B))$
for every $I\in \operatorname {Res}(\mathcal {I}(B))$![]() , cf. [Reference Kwaśniewski and Meyer29, Definition 5.2].
, cf. [Reference Kwaśniewski and Meyer29, Definition 5.2].
(1) For each $p\in \operatorname {Prime}(A)$
 there is a largest restricted ideal $\pi (p)$
there is a largest restricted ideal $\pi (p)$ in $A$
in $A$ that is contained in $p$
that is contained in $p$ . Moreover, $\pi (p)=\pi (q)$
. Moreover, $\pi (p)=\pi (q)$ defines an open equivalence relation $\sim$
defines an open equivalence relation $\sim$ on $\operatorname {Prime}(A)$
on $\operatorname {Prime}(A)$ .
.(2) The map $\varrho :\operatorname {Prime}(B)\ni P\longmapsto [P\cap A]\in \operatorname {Prime}(A)/\sim$
 is well defined and continuous.
is well defined and continuous.
Proof. It is well known that $\check {A}=\operatorname {Prime}(A)$![]() , cf. [Reference Kwaśniewski and Meyer29, Corollary 3.9]. The rest follows from the results of [Reference Kwaśniewski and Meyer29] where both $A$
, cf. [Reference Kwaśniewski and Meyer29, Corollary 3.9]. The rest follows from the results of [Reference Kwaśniewski and Meyer29] where both $A$![]() and $B$
and $B$![]() are assumed to be $C^*$
are assumed to be $C^*$![]() -algebras, but a close inspection of the proofs shows that they work when $B$
-algebras, but a close inspection of the proofs shows that they work when $B$![]() is an arbitrary Banach algebra. Namely, the proof of [Reference Kwaśniewski and Meyer29, Lemma 5.1] (which only uses the properties of Galois connection and that ideals in $A$
is an arbitrary Banach algebra. Namely, the proof of [Reference Kwaśniewski and Meyer29, Lemma 5.1] (which only uses the properties of Galois connection and that ideals in $A$![]() have approximate units) shows that for symmetric inclusions, we have $I\in \operatorname {Res}(\mathcal {I}(B))$
have approximate units) shows that for symmetric inclusions, we have $I\in \operatorname {Res}(\mathcal {I}(B))$![]() if and only if $\operatorname {Ex}(I)=\overline {IB}$
if and only if $\operatorname {Ex}(I)=\overline {IB}$![]() . This characterization of elements in $\operatorname {Res}(\mathcal {I}(B))$
. This characterization of elements in $\operatorname {Res}(\mathcal {I}(B))$![]() is used in the proof of [Reference Kwaśniewski and Meyer29, Lemma 5.4], to conclude in [Reference Kwaśniewski and Meyer29, Corollary 5.5] that the conditions (JR), (FR1) and (MIf) defined in [Reference Kwaśniewski and Meyer29] hold. By [Reference Kwaśniewski and Meyer29, Lemma 4.1 and Theorem 4.5] we have (1), $\pi$
is used in the proof of [Reference Kwaśniewski and Meyer29, Lemma 5.4], to conclude in [Reference Kwaśniewski and Meyer29, Corollary 5.5] that the conditions (JR), (FR1) and (MIf) defined in [Reference Kwaśniewski and Meyer29] hold. By [Reference Kwaśniewski and Meyer29, Lemma 4.1 and Theorem 4.5] we have (1), $\pi$![]() induces a homeomorphism from quotient space $\operatorname {Prime}(A)/\sim$
induces a homeomorphism from quotient space $\operatorname {Prime}(A)/\sim$![]() onto the space of prime elements in $\operatorname {Res}(\mathcal {I}(B))$
onto the space of prime elements in $\operatorname {Res}(\mathcal {I}(B))$![]() , and $\operatorname {Res}(\mathcal {I}(B))\cong \operatorname {Ex}(\mathcal {I}(A))$
, and $\operatorname {Res}(\mathcal {I}(B))\cong \operatorname {Ex}(\mathcal {I}(A))$![]() is a spatial locale (as it is embedded by a frame morphism in the spatial locale $\mathcal {I}(A)$
is a spatial locale (as it is embedded by a frame morphism in the spatial locale $\mathcal {I}(A)$![]() ). Now (2) follows from [Reference Kwaśniewski and Meyer29, Lemma 4.8] whose proof uses that $B$
). Now (2) follows from [Reference Kwaśniewski and Meyer29, Lemma 4.8] whose proof uses that $B$![]() is a $C^*$
is a $C^*$![]() -algebra only to conclude that $\operatorname {Res}(\mathcal {I}(B))$
-algebra only to conclude that $\operatorname {Res}(\mathcal {I}(B))$![]() is a spatial locale, but as noted above we already have this property in our setting.
is a spatial locale, but as noted above we already have this property in our setting.
Definition 6.17 cf. [Reference Kwaśniewski and Meyer29, Definitions 4.4, 4.10]
We call $\operatorname {Prime}(A)/{\sim }$![]() and $\varrho \colon \operatorname {Prime}(B) \to \operatorname {Prime}(A)/{\sim }$
and $\varrho \colon \operatorname {Prime}(B) \to \operatorname {Prime}(A)/{\sim }$![]() in lemma 6.16 the quasi-orbit space and the quasi-orbit map for the inclusion $A\subseteq B$
in lemma 6.16 the quasi-orbit space and the quasi-orbit map for the inclusion $A\subseteq B$![]() . For an action $\varphi :G\to \operatorname {Homeo}(X)$
. For an action $\varphi :G\to \operatorname {Homeo}(X)$![]() the quasi-orbit space is defined as the quotient space $\mathcal {O}(X)=X/\sim$
the quasi-orbit space is defined as the quotient space $\mathcal {O}(X)=X/\sim$![]() for the equivalence relation $x\sim y$
for the equivalence relation $x\sim y$![]() if and only if $\overline {Gx}=\overline {Gy}$
if and only if $\overline {Gx}=\overline {Gy}$![]() , where $\overline {Gx}:=\overline {\{\varphi _t(x):t\in G\}}$
, where $\overline {Gx}:=\overline {\{\varphi _t(x):t\in G\}}$![]() is the closure of the orbit of $x$
is the closure of the orbit of $x$![]() , see [Reference Effros and Hahn15].
, see [Reference Effros and Hahn15].
Proposition 6.18 Assume $X$![]() is second countable and let $F_{\mathcal {R}}(\alpha,\,u)$
is second countable and let $F_{\mathcal {R}}(\alpha,\,u)$![]() be a crossed product. The quasi-orbit space for the inclusion $C_0(X)\subseteq F_{\mathcal {R}}(\alpha,\,u)$
be a crossed product. The quasi-orbit space for the inclusion $C_0(X)\subseteq F_{\mathcal {R}}(\alpha,\,u)$![]() coincides with the quasi-orbit space $\mathcal {O}(X)$
coincides with the quasi-orbit space $\mathcal {O}(X)$![]() for the action. Thus, the quotient map $X\ni x\mapsto [x]\in \mathcal {O}(X)$
for the action. Thus, the quotient map $X\ni x\mapsto [x]\in \mathcal {O}(X)$![]() is open and we have a continuous quasi-orbit map
is open and we have a continuous quasi-orbit map
Moreover, $\varrho$![]() is a homeomorphism if and only if $C_0(X)$
is a homeomorphism if and only if $C_0(X)$![]() separates ideals in $F_{\mathcal {R}}(\alpha,\,u)$
separates ideals in $F_{\mathcal {R}}(\alpha,\,u)$![]() .
.
Proof. Let $A:=C_0(X)$![]() and $B:=F_{\mathcal {R}}(\alpha,\,u)$
and $B:=F_{\mathcal {R}}(\alpha,\,u)$![]() . By lemma 5.14, we have $\operatorname {Res}(\mathcal {I}(B))=\{C_0(U):U\in \mathcal {I}^\varphi (X)\}$
. By lemma 5.14, we have $\operatorname {Res}(\mathcal {I}(B))=\{C_0(U):U\in \mathcal {I}^\varphi (X)\}$![]() and $\operatorname {Ex}(C_0(U))=F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$
and $\operatorname {Ex}(C_0(U))=F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$![]() for $U\in \mathcal {I}^\varphi (X)$
for $U\in \mathcal {I}^\varphi (X)$![]() . For each $U\in \mathcal {I}^\varphi (X)$
. For each $U\in \mathcal {I}^\varphi (X)$![]() , $C_0(U)$
, $C_0(U)$![]() and $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$
and $F_{\mathcal {R}^U}(\alpha ^U,\,u^U)$![]() have the same approximate unit. Thus, the inclusion $A\subseteq B$
have the same approximate unit. Thus, the inclusion $A\subseteq B$![]() is symmetric and we may apply lemma 6.16. The canonical homeomorphism $X\ni x\mapsto C_0(X\setminus \{x\})\in \operatorname {Prime}(A)$
is symmetric and we may apply lemma 6.16. The canonical homeomorphism $X\ni x\mapsto C_0(X\setminus \{x\})\in \operatorname {Prime}(A)$![]() descends to a homeomorphism between the orbit quotient spaces, as for each $x\in X$
descends to a homeomorphism between the orbit quotient spaces, as for each $x\in X$![]() , the largest restricted ideal contained in $C_0(X\setminus \{x\})$
, the largest restricted ideal contained in $C_0(X\setminus \{x\})$![]() is $\pi (C_0(X\setminus \{x\}))=C_0(X\setminus \overline {Gx})$
is $\pi (C_0(X\setminus \{x\}))=C_0(X\setminus \overline {Gx})$![]() , and so $x\sim y$
, and so $x\sim y$![]() if and only if $\pi (C_0(X\setminus \{x\}))=\pi (C_0(X\setminus \{y\}))$
if and only if $\pi (C_0(X\setminus \{x\}))=\pi (C_0(X\setminus \{y\}))$![]() . The rest follows now from lemma 6.16.
. The rest follows now from lemma 6.16.
Corollary 6.19 Assume $X$![]() is second countable. An action $\varphi$
is second countable. An action $\varphi$![]() is residually topologically free if and only if for every residually reduced $F_{\mathcal {R}}(\alpha,\,u)$
is residually topologically free if and only if for every residually reduced $F_{\mathcal {R}}(\alpha,\,u)$![]() the quasi-orbit map is a homeomorphism $\operatorname {Prime} (F_{\mathcal {R}}(\alpha,\,u))\cong \mathcal {O}(X)$
the quasi-orbit map is a homeomorphism $\operatorname {Prime} (F_{\mathcal {R}}(\alpha,\,u))\cong \mathcal {O}(X)$![]() .
.
Remark 6.20 For $C^*$![]() -algebraic crossed products the homeomorphism between the primitive ideal space and quasi-orbit space was already proved in [Reference Effros and Hahn15, Corollary 5.16] and [Reference Zeller-Meier43, Proposition 4.17] under the additional assumptions that $G$
-algebraic crossed products the homeomorphism between the primitive ideal space and quasi-orbit space was already proved in [Reference Effros and Hahn15, Corollary 5.16] and [Reference Zeller-Meier43, Proposition 4.17] under the additional assumptions that $G$![]() is amenable, countable and acts freely on $X$
is amenable, countable and acts freely on $X$![]() . That freeness can be relaxed to residual topological freeness was noted in [Reference Renault38, Corollary 4.9]. Also in [Reference Renault38, Remark 4.10] it was suggested that the amenability (of the action) of $G$
. That freeness can be relaxed to residual topological freeness was noted in [Reference Renault38, Corollary 4.9]. Also in [Reference Renault38, Remark 4.10] it was suggested that the amenability (of the action) of $G$![]() can be relaxed to exactness of the action, which was formalized in [Reference Sierakowski40, Theorem 1.20].
can be relaxed to exactness of the action, which was formalized in [Reference Sierakowski40, Theorem 1.20].
Acknowledgements
The authors were supported by the National Science Center (NCN) grant no. 2019/35/B/ST1/02684. We would like to thank Andrew McKee for a number of useful comments, especially those on amenable actions, and to an anonymous reviewer for a number of suggestions that improved the presentation.