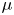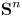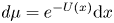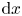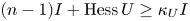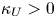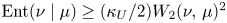1. Transportation on the sphere
Optimal transportation involves moving unit mass from one probability distribution to another, at minimal cost, where the cost is measured by Wasserstein's distance.
Definition Let $(M,\,d)$![]() be a compact metric space and let $\mu$
be a compact metric space and let $\mu$![]() and $\nu$
and $\nu$![]() be probability measures on $M$
be probability measures on $M$![]() . Then for $1\leq p<\infty$
. Then for $1\leq p<\infty$![]() , Wasserstein's distance from $\mu$
, Wasserstein's distance from $\mu$![]() to $\nu$
to $\nu$![]() is $W_p(\nu,\, \mu )$
is $W_p(\nu,\, \mu )$![]() , where
, where

where the probability measure $\pi$![]() has marginals $\nu$
has marginals $\nu$![]() and $\mu$
and $\mu$![]() (see [Reference Dudley8, Reference Villani14]).
(see [Reference Dudley8, Reference Villani14]).
Transportation inequalities are results that bound the transportation cost $W_p(\nu,\, \mu )^p$![]() in terms of $\mu$
in terms of $\mu$![]() , $\nu$
, $\nu$![]() and geometrical quantities of $(M,\,d)$
and geometrical quantities of $(M,\,d)$![]() . Typically, one chooses $\mu$
. Typically, one chooses $\mu$![]() to satisfy special conditions, and then one imposes minimal hypotheses on $\nu$
to satisfy special conditions, and then one imposes minimal hypotheses on $\nu$![]() . In this section, we consider the case where $(M,\,d)$
. In this section, we consider the case where $(M,\,d)$![]() is the unit sphere ${\bf S}^2$
is the unit sphere ${\bf S}^2$![]() in ${\bf R}^3$
in ${\bf R}^3$![]() , and obtain transportation inequalities by vector calculus. In section two, we extend these methods to a connected, compact and $C^\infty$
, and obtain transportation inequalities by vector calculus. In section two, we extend these methods to a connected, compact and $C^\infty$![]() smooth Riemannian manifold $(M,\,d)$
smooth Riemannian manifold $(M,\,d)$![]() .
.
On ${\bf S}^2$![]() , let $\theta \in [0,\, 2\pi )$
, let $\theta \in [0,\, 2\pi )$![]() be the longitude and $\phi \in [0,\, \pi ]$
be the longitude and $\phi \in [0,\, \pi ]$![]() the colatitude, so the area measure is ${\rm d}x=\sin \phi \, d\phi d\theta$
the colatitude, so the area measure is ${\rm d}x=\sin \phi \, d\phi d\theta$![]() . Let $ABC$
. Let $ABC$![]() be a spherical triangle where $A$
be a spherical triangle where $A$![]() is the North Pole; then by [Reference Kimura and Okamoto10] the Green's function $G(B,\,C)=-(4\pi )^{-1}\log (1-\cos d(B,\,C))$
is the North Pole; then by [Reference Kimura and Okamoto10] the Green's function $G(B,\,C)=-(4\pi )^{-1}\log (1-\cos d(B,\,C))$![]() may be expressed in terms of longitude and co latitude of $B$
may be expressed in terms of longitude and co latitude of $B$![]() and $C$
and $C$![]() via the spherical cosine formula. A related cost function is listed in [Reference Villani14], p 972. Given probability measures $\mu$
via the spherical cosine formula. A related cost function is listed in [Reference Villani14], p 972. Given probability measures $\mu$![]() and $\nu$
and $\nu$![]() on ${\bf S}^2$
on ${\bf S}^2$![]() , we can form
, we can form
with gradient in the $x$![]() variable
variable
Proposition 1.1 Let $\mu$![]() and $\nu$
and $\nu$![]() be nonatomic probability measures on ${\bf S}^2$
be nonatomic probability measures on ${\bf S}^2$![]() . Then
. Then
Proof. The Green's function is chosen so that $\nabla \cdot \nabla G(B,\,C)=\delta _B(C)-1/(4\pi )$![]() in the sense of distributions. Given non-atomic probability measures $\mu$
in the sense of distributions. Given non-atomic probability measures $\mu$![]() and $\nu$
and $\nu$![]() on ${\bf S}^2$
on ${\bf S}^2$![]() , their difference $\mu -\nu$
, their difference $\mu -\nu$![]() is orthogonal to the constants on ${\bf S}^2,$
is orthogonal to the constants on ${\bf S}^2,$![]() so for a $1$
so for a $1$![]() -Lipschitz function $\varphi : {\bf S}^2\rightarrow {\bf R}$
-Lipschitz function $\varphi : {\bf S}^2\rightarrow {\bf R}$![]() , we have
, we have

so by Kantorovich's duality theorem [Reference Dudley8], the Wasserstein transportation distance is bounded by
Definition Suppose that $\mu$![]() is a probability measure and $\nu$
is a probability measure and $\nu$![]() is a probability measure that is absolutely continuous with respect to $\mu$
is a probability measure that is absolutely continuous with respect to $\mu$![]() , so $d\nu =vd\mu$
, so $d\nu =vd\mu$![]() for some probability density function $v\in L^1(\mu )$
for some probability density function $v\in L^1(\mu )$![]() . Then the relative entropy of $\nu$
. Then the relative entropy of $\nu$![]() with respect to $\mu$
with respect to $\mu$![]() is
is
where $0\leq {\hbox {Ent}}(\nu \mid \mu ) \leq \infty$![]() by Jensen's inequality.
by Jensen's inequality.
At $x\in {\bf S}^2$![]() , we have tangent space $T_s{\bf S}^2=\{ y\in {\bf R}^3: x\cdot y=0\}$
, we have tangent space $T_s{\bf S}^2=\{ y\in {\bf R}^3: x\cdot y=0\}$![]() . For $y\in T_x{\bf S}^2$
. For $y\in T_x{\bf S}^2$![]() with $\Vert y\Vert =1$
with $\Vert y\Vert =1$![]() , we consider $\exp _x(ty)=x\cos t+y\sin t$
, we consider $\exp _x(ty)=x\cos t+y\sin t$![]() so that $\exp _x(0)=x$
so that $\exp _x(0)=x$![]() , $\Vert \exp _x(ty)\Vert =1$
, $\Vert \exp _x(ty)\Vert =1$![]() and $(d/{\rm d}t)_{t=0}\exp _x(ty)=y$
and $(d/{\rm d}t)_{t=0}\exp _x(ty)=y$![]() ; hence $\exp _x:T_x{\bf S}^2\rightarrow {\bf S}^2$
; hence $\exp _x:T_x{\bf S}^2\rightarrow {\bf S}^2$![]() gives the exponential map. We let $J_{\exp _x}$
gives the exponential map. We let $J_{\exp _x}$![]() be the Jacobian determinant of this map.
be the Jacobian determinant of this map.
Suppose that $\mu ({\rm d}x)=e^{-U (x)}{\rm d}x$![]() is a probability measure and $\nu$
is a probability measure and $\nu$![]() is a probability measure that is absolutely continuous with respect to $\mu$
is a probability measure that is absolutely continuous with respect to $\mu$![]() , so $d\nu =vd\mu$
, so $d\nu =vd\mu$![]() . We say that a Borel function $\Psi :{\bf S}^2\rightarrow {\bf S}^2$
. We say that a Borel function $\Psi :{\bf S}^2\rightarrow {\bf S}^2$![]() induces $\nu$
induces $\nu$![]() from $\mu$
from $\mu$![]() if $\int f(y)\nu ({\rm d}y)=\int f(\Psi (x))\mu ({\rm d}x )$
if $\int f(y)\nu ({\rm d}y)=\int f(\Psi (x))\mu ({\rm d}x )$![]() for all $f\in C({\bf S}^2; {\bf R})$
for all $f\in C({\bf S}^2; {\bf R})$![]() . McCann [Reference McCann12] showed that there exists $\Psi$
. McCann [Reference McCann12] showed that there exists $\Psi$![]() that gives the optimal transport strategy for the $W_2$
that gives the optimal transport strategy for the $W_2$![]() metric; further, there exists a Lipschitz function $\psi : {\bf S}^2\rightarrow {\bf R}$
metric; further, there exists a Lipschitz function $\psi : {\bf S}^2\rightarrow {\bf R}$![]() such that $\Psi (x)=\exp _x(\nabla \psi (x))$
such that $\Psi (x)=\exp _x(\nabla \psi (x))$![]() ; so that
; so that
Talagrand developed $T_p$![]() inequalities in which $W_p(\nu,\, \mu )^p$
inequalities in which $W_p(\nu,\, \mu )^p$![]() is bounded in terms of ${\hbox {Ent}}(\nu \mid \mu )$
is bounded in terms of ${\hbox {Ent}}(\nu \mid \mu )$![]() , as in [Reference Villani14], p 569. In [Reference Cordero-Erausquin5] and [Reference Cordero-Erausquin, McCann and Schmuckensläger6], the authors obtain some functional inequalities that are related to $T_p$
, as in [Reference Villani14], p 569. In [Reference Cordero-Erausquin5] and [Reference Cordero-Erausquin, McCann and Schmuckensläger6], the authors obtain some functional inequalities that are related to $T_p$![]() inequalities. Here we offer an approach that is more direct, and uses only basic differential geometry to augment McCann's fundamental result. The key point is an explicit formula for the relative entropy in terms of the optimal transport maps.
inequalities. Here we offer an approach that is more direct, and uses only basic differential geometry to augment McCann's fundamental result. The key point is an explicit formula for the relative entropy in terms of the optimal transport maps.
Lemma 1.2 Suppose that $\nu$![]() has finite relative entropy with respect to $\mu,$
has finite relative entropy with respect to $\mu,$![]() and let
and let
let $\Psi _t(x)=\exp _x(t\nabla \psi (x))$![]() for $t\in [0,\,1]$
for $t\in [0,\,1]$![]() . Then the relative entropy satisfies
. Then the relative entropy satisfies

where $A$![]() is positive definite, $H$
is positive definite, $H$![]() is symmetric and $A+H$
is symmetric and $A+H$![]() is also positive definite, and
is also positive definite, and
If $\psi \in C^2,$![]() then equality holds in (1.8).
then equality holds in (1.8).
Proof. To express the relative entropy in terms of the transportation map, we adapt an argument from [Reference Blower1]. We have ${\hbox {Ent}}(\nu \mid \mu )=\int _{{\bf S}^2} \log v(\Psi (x))\mu ({\rm d}x)$![]() , where the integrand is
, where the integrand is
where the final term arises from the Jacobian of the change of variable $y=\Psi (x)$![]() , where $\Psi =\Psi _1$
, where $\Psi =\Psi _1$![]() and $\Psi _t(x)=\exp _x(t\nabla \psi (x))$
and $\Psi _t(x)=\exp _x(t\nabla \psi (x))$![]() . We compute this Jacobian by the chain rule for derivatives with respect to $x$
. We compute this Jacobian by the chain rule for derivatives with respect to $x$![]() . Specifically by [Reference Cordero-Erausquin, McCann and Schmuckensläger6] p 622, we have ${\hbox {Hess}}(\psi (x)+d(x,\,y)^2/2)\geq 0$
. Specifically by [Reference Cordero-Erausquin, McCann and Schmuckensläger6] p 622, we have ${\hbox {Hess}}(\psi (x)+d(x,\,y)^2/2)\geq 0$![]() and
and
where $J_{\exp _x}$![]() is the Jacobian of $\exp _x:T_x{\bf S}^2\rightarrow {\bf S}^2$
is the Jacobian of $\exp _x:T_x{\bf S}^2\rightarrow {\bf S}^2$![]() and ${\hbox {Hess}}=D_x^2$
and ${\hbox {Hess}}=D_x^2$![]() is the Hessian, where the expression is evaluated at $y=\exp _x(\nabla \psi (x))$
is the Hessian, where the expression is evaluated at $y=\exp _x(\nabla \psi (x))$![]() . For $x\in {\bf S}^2$
. For $x\in {\bf S}^2$![]() and $\tau \in {\bf R}^3$
and $\tau \in {\bf R}^3$![]() such that $x\cdot \tau =0$
such that $x\cdot \tau =0$![]() , we have $\tau \in T_x{\bf S}^2$
, we have $\tau \in T_x{\bf S}^2$![]() and
and
see [Reference Cordero-Erausquin5]. By a vector calculus computation, which we replicate from [Reference Cordero-Erausquin5], one finds
With $\psi :{\bf S}^2\rightarrow {\bf R}$![]() we have $\nabla \psi (x)\perp x$
we have $\nabla \psi (x)\perp x$![]() , so $0=x\cdot \nabla \psi (x),$
, so $0=x\cdot \nabla \psi (x),$![]() hence $0=\nabla \psi (x)+{\hbox {Hess}}(\psi (x)) x$
hence $0=\nabla \psi (x)+{\hbox {Hess}}(\psi (x)) x$![]() . We write $\theta =\Vert \nabla \psi (x)\Vert$
. We write $\theta =\Vert \nabla \psi (x)\Vert$![]() for the angle between $x$
for the angle between $x$![]() and $\Psi (x)$
and $\Psi (x)$![]() so
so
let $v=x\times \theta ^{-1}\nabla \psi (x)$![]() where $\times$
where $\times$![]() denotes the usual vector product; then $\{ x,\, \theta ^{-1}\nabla \psi (x),\, v\}$
denotes the usual vector product; then $\{ x,\, \theta ^{-1}\nabla \psi (x),\, v\}$![]() gives an orthonormal basis of ${\bf R}^3$
gives an orthonormal basis of ${\bf R}^3$![]() . Hence
. Hence

and we obtain (1.13) from the final factor. Then by spherical trigonometry, we have
so we have $\langle \nabla _x \cos d(x,\,y),\, \tau \rangle =\langle y,\, \tau \rangle$![]() and $\langle {\hbox {Hess}}_x\cos d(x,\,y)\tau,\, \tau \rangle =-(\cos d(x,\,y)) \Vert \tau \Vert ^2$
and $\langle {\hbox {Hess}}_x\cos d(x,\,y)\tau,\, \tau \rangle =-(\cos d(x,\,y)) \Vert \tau \Vert ^2$![]() ; so
; so

hence $A$![]() is positive definite and is a rank-one perturbation of a multiple of the identity matrix. Note that the formulas degenerate on the cut locus $d(x,\,y)=\pi ;$
is positive definite and is a rank-one perturbation of a multiple of the identity matrix. Note that the formulas degenerate on the cut locus $d(x,\,y)=\pi ;$![]() consider the international date line opposite the Greenwich meridian.
consider the international date line opposite the Greenwich meridian.
We have
in which
and we can combine the first two terms in (1.16) by the divergence theorem so
Hence from (1.11) we have
in which the Alexandrov Hessian [Reference Cordero-Erausquin, McCann and Schmuckensläger6], [Reference Villani14] p 363 satisfies
where $\Delta _D\psi$![]() is the distributional derivative of the Lipschitz function $\psi$
is the distributional derivative of the Lipschitz function $\psi$![]() ; so we recognize (1.8).
; so we recognize (1.8).
We have an orthonormal basis

for ${\bf R}^3$![]() in which the final two vectors give an orthonormal basis for $T_x{\bf S}^2$
in which the final two vectors give an orthonormal basis for $T_x{\bf S}^2$![]() . Then
. Then

and

hence $A$![]() and $H$
and $H$![]() have the form
have the form

with respect to the stated basis of $T_x{\bf S}^2$![]() .
.
The function $f(x)=x-1-\log x$![]() for $x>0$
for $x>0$![]() is convex and takes its minimum value at $f(1)=0$
is convex and takes its minimum value at $f(1)=0$![]() . Let $T$
. Let $T$![]() be a self-adjoint matrix with eigenvalues $\lambda _1\geq \dots \geq \lambda _n$
be a self-adjoint matrix with eigenvalues $\lambda _1\geq \dots \geq \lambda _n$![]() where $\lambda _n>-1$
where $\lambda _n>-1$![]() ; then the Carleman determinant of $I+T$
; then the Carleman determinant of $I+T$![]() is $\det _2(I+T)=\prod _{j=1}^n (1+\lambda _j)e^{-\lambda _j}$
is $\det _2(I+T)=\prod _{j=1}^n (1+\lambda _j)e^{-\lambda _j}$![]() . Since $A+H$
. Since $A+H$![]() is positive definite, as in [Reference Blower1] corollary 4.3, we can apply the spectral theorem to compute the Carleman determinant and show that
is positive definite, as in [Reference Blower1] corollary 4.3, we can apply the spectral theorem to compute the Carleman determinant and show that
so

Proposition 1.3 Suppose that the Hessian matrix of $U$![]() satisfies
satisfies
for some $\kappa _U>0$![]() . Then $\mu$
. Then $\mu$![]() satisfies the transportation inequality
satisfies the transportation inequality
This applies in particular when $\mu$![]() is normalized surface area measure.
is normalized surface area measure.
Proof. Let $K:[0,\, \pi )\rightarrow {\bf R}$![]() be the function
be the function

Then from (1.13) and (1.26) we have

Considering the final integral in (1.8), we have
which has constant speed $\Vert {\frac {\partial \Psi _t(x) }{\partial t}}\Vert =\Vert \nabla \psi (x)\Vert$![]() and $\langle {\frac {\partial \Psi _t(x) }{\partial t}},\, \Psi _t(x)\rangle =0;$
and $\langle {\frac {\partial \Psi _t(x) }{\partial t}},\, \Psi _t(x)\rangle =0;$![]() also
also
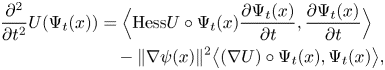
where the final term is zero since $\nabla U\circ \Psi _t(x)$![]() is in the tangent space at $\Psi _t(x)$
is in the tangent space at $\Psi _t(x)$![]() , hence is perpendicular to $\Psi _t(x)$
, hence is perpendicular to $\Psi _t(x)$![]() . We therefore have the crucial inequality
. We therefore have the crucial inequality

To simplify the function $K$![]() , we recall from [Reference Gradsteyn and Ryzhik9] 8.342 the Maclaurin series
, we recall from [Reference Gradsteyn and Ryzhik9] 8.342 the Maclaurin series

where we have introduced Euler's $\Gamma$![]() function and Riemann's $\zeta$
function and Riemann's $\zeta$![]() function, so
function, so

Now we consider (1.32) with the hypothesis (1.27) in force. The Carleman determinant contributes a nonnegative term as in (1.25), while the final integral in (1.32) combines with the integral of $K(\Vert \nabla \psi (x)\Vert )$![]() to give
to give

When $\mu$![]() is normalized surface area, $U$
is normalized surface area, $U$![]() is a constant and the hypothesis (1.27) holds with $\kappa _U=1$
is a constant and the hypothesis (1.27) holds with $\kappa _U=1$![]() .
.
2. Transportation on compact Riemannian manifolds
Let $M$![]() be a connected, compact and $C^\infty$
be a connected, compact and $C^\infty$![]() smooth Riemannian manifold of dimension $n$
smooth Riemannian manifold of dimension $n$![]() without boundary, and let $g$
without boundary, and let $g$![]() be the Riemannian metric tensor, giving metric $d$
be the Riemannian metric tensor, giving metric $d$![]() . Let $\mu ({\rm d}x)=e^{-U(x)}{\rm d}x$
. Let $\mu ({\rm d}x)=e^{-U(x)}{\rm d}x$![]() be a probability measure on $M$
be a probability measure on $M$![]() where ${\rm d}x$
where ${\rm d}x$![]() is Riemannian measure and $U\in C^2(M; {\bf R})$
is Riemannian measure and $U\in C^2(M; {\bf R})$![]() . Suppose that $\nu$
. Suppose that $\nu$![]() is a probability measure on $M$
is a probability measure on $M$![]() that is of finite relative entropy with respect to $\mu$
that is of finite relative entropy with respect to $\mu$![]() . Then by McCann's theory [Reference McCann12], there exists a Lipschitz function $\psi :M\rightarrow {\bf R}$
. Then by McCann's theory [Reference McCann12], there exists a Lipschitz function $\psi :M\rightarrow {\bf R}$![]() such that $\Psi (x)=\exp _x(\nabla \psi (x))$
such that $\Psi (x)=\exp _x(\nabla \psi (x))$![]() induces $\nu$
induces $\nu$![]() from $\mu$
from $\mu$![]() . then we let $\Psi _t(x)=\exp _x(t\nabla \psi (x))$
. then we let $\Psi _t(x)=\exp _x(t\nabla \psi (x))$![]() . We proceed to compute quantities which we need for our extension of lemma 1.2.
. We proceed to compute quantities which we need for our extension of lemma 1.2.
Given distinct points $x,\,y\in M$![]() , we suppose that $x=\exp _y(\xi )$
, we suppose that $x=\exp _y(\xi )$![]() , and for $w\in T_yM$
, and for $w\in T_yM$![]() introduce
introduce
so that $t\mapsto \gamma (s,\,t)$![]() is a geodesic, and in particular $\gamma (0,\,t)$
is a geodesic, and in particular $\gamma (0,\,t)$![]() is the geodesic from $y=\gamma (0,\,0)$
is the geodesic from $y=\gamma (0,\,0)$![]() to $x=\gamma (0,\,1)$
to $x=\gamma (0,\,1)$![]() . When $y=\exp _x(\nabla \psi (x))$
. When $y=\exp _x(\nabla \psi (x))$![]() for a Lipschitz function $\psi :M\rightarrow {\bf R}$
for a Lipschitz function $\psi :M\rightarrow {\bf R}$![]() , we can determine $\xi$
, we can determine $\xi$![]() as follows. Let $\phi (z)=-\psi (z)$
as follows. Let $\phi (z)=-\psi (z)$![]() and introduce its infimal convolution
and introduce its infimal convolution
which is attained at $x$![]() since $y=\exp _x(\nabla \psi (x))=\exp _x(-\nabla \phi (x))$
since $y=\exp _x(\nabla \psi (x))=\exp _x(-\nabla \phi (x))$![]() . Now $\phi ^{cc}(x)=\phi (x)$
. Now $\phi ^{cc}(x)=\phi (x)$![]() , so
, so
where the infimum is attained at $y$![]() since $\phi (x)+\phi ^c(y)=d(x,\,y)^2/2$
since $\phi (x)+\phi ^c(y)=d(x,\,y)^2/2$![]() . By lemma 2 of [Reference McCann12], $\phi ^c$
. By lemma 2 of [Reference McCann12], $\phi ^c$![]() is Lipschitz and
is Lipschitz and
The speed of $\gamma (0,\,t)$![]() is given by
is given by

Let $R$![]() be the curvature of the Levi–Civita derivation $\nabla$
be the curvature of the Levi–Civita derivation $\nabla$![]() so
so
Then by [Reference Pedersen13] p 36, for all $Y\in T_xM$![]() , the curvature operator $R_Y: X\mapsto R(X,\,Y)Y$
, the curvature operator $R_Y: X\mapsto R(X,\,Y)Y$![]() is self-adjoint with respect to the scalar product on $T_xM$
is self-adjoint with respect to the scalar product on $T_xM$![]() . Also
. Also
satisfies the initial conditions
and Jacobi's differential equation [Reference Chavel4] (2.43)

By calculating the first variation of the length formula [Reference Pedersen13] p 161, one shows that
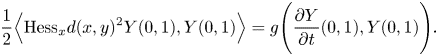
Assume that there are no conjugate points on $\gamma (s,\,t)$![]() . Then by varying $w$
. Then by varying $w$![]() , we can make $Y(0,\,1)$
, we can make $Y(0,\,1)$![]() cover a neighbourhood of $0$
cover a neighbourhood of $0$![]() in $T_xM$
in $T_xM$![]() . Let
. Let
and
Let $J_{\exp _x}(v)$![]() be the Jacobian of the map $T_xM\rightarrow M$
be the Jacobian of the map $T_xM\rightarrow M$![]() given by $v\mapsto \exp _x(v)$
given by $v\mapsto \exp _x(v)$![]() , as in (3.4) of [Reference Cabre3].
, as in (3.4) of [Reference Cabre3].
Lemma 2.1 Suppose that $\Psi _t (x)=\exp _x(t \nabla \psi (x))$![]() , where $\Psi _1$
, where $\Psi _1$![]() induces the probability measure $\nu$
induces the probability measure $\nu$![]() from $\mu$
from $\mu$![]() and gives the optimal transport map for the $W_2$
and gives the optimal transport map for the $W_2$![]() metric. Then the relative entropy satisfies
metric. Then the relative entropy satisfies

where $H$![]() is symmetric and $A+H$
is symmetric and $A+H$![]() is also positive definite. If $\psi \in C^2(M; {\bf R})$
is also positive definite. If $\psi \in C^2(M; {\bf R})$![]() , then equality holds in (2.12).
, then equality holds in (2.12).
Proof. This is similar to lemma 1.2. As in (1.5), we have

and by standard calculations [Reference Pedersen13] p 32 we have
since $\Psi _t(x)$![]() is a geodesic.
is a geodesic.
The curvature operator is the symmetic operator $R_Z:Y\mapsto R(Z,\,Y)Z$![]() . If $M$
. If $M$![]() has nonnegative Ricci curvature so that $R_Z\geq 0$
has nonnegative Ricci curvature so that $R_Z\geq 0$![]() as a matrix for all $Z$
as a matrix for all $Z$![]() , then we have
, then we have
by (3.4) of [Ca].
The following result recovers the Lichnérowicz integral, as in (4.16) of [Reference Blower1] and (1.1) of [Reference Deuschel and Stroock7]. This integral also appears implicitly in the Hessian calculations in appendix D of [Reference Lott and Villani11]. Let $\Vert H\Vert _{HS}$![]() be the Hilbert–Schmidt norm of $H$
be the Hilbert–Schmidt norm of $H$![]() .
.
Proposition 2.2 Suppose that $\psi \in C^2(M; {\bf R})$![]() and $\Psi _\tau (x)=\exp _x(\tau \nabla \psi (x))$
and $\Psi _\tau (x)=\exp _x(\tau \nabla \psi (x))$![]() induces a probability measure $\nu _\tau$
induces a probability measure $\nu _\tau$![]() from $\mu$
from $\mu$![]() such that $\Psi _\tau$
such that $\Psi _\tau$![]() is the optimal transport map for the $W_2$
is the optimal transport map for the $W_2$![]() metric. Then
metric. Then

Proof. For small $\tau >0$![]() , we rescale $\psi$
, we rescale $\psi$![]() to $\tau \psi$
to $\tau \psi$![]() and consider $y=\exp _x(\tau \nabla \psi (x))$
and consider $y=\exp _x(\tau \nabla \psi (x))$![]() ; then we return to $x$
; then we return to $x$![]() along a geodesic $\gamma _\tau (t)=\exp _y(-t\nabla (-\tau \psi )^c(y))$
along a geodesic $\gamma _\tau (t)=\exp _y(-t\nabla (-\tau \psi )^c(y))$![]() for $0\leq t\leq 1$
for $0\leq t\leq 1$![]() with constant speed $\tau \Vert \nabla \psi (x)\Vert$
with constant speed $\tau \Vert \nabla \psi (x)\Vert$![]() . Observe that $\tau \psi (x)=(-\tau \psi )^c(y)-\tau ^2\Vert \nabla \psi (x)\Vert ^2/2$
. Observe that $\tau \psi (x)=(-\tau \psi )^c(y)-\tau ^2\Vert \nabla \psi (x)\Vert ^2/2$![]() , and $\nabla _xd(x,\,y)^2/2=-\exp _x^{-1}(y)=-\tau \nabla \psi (x)$
, and $\nabla _xd(x,\,y)^2/2=-\exp _x^{-1}(y)=-\tau \nabla \psi (x)$![]() and $\nabla _yd(x,\,y)^2/2=-\exp _y^{-1}(x)=\nabla (-\tau \psi )^c(y)$
and $\nabla _yd(x,\,y)^2/2=-\exp _y^{-1}(x)=\nabla (-\tau \psi )^c(y)$![]() by Gauss's Lemma. Recalling that the curvature operator is self-adjoint by page 36 of [Reference Pedersen13], we choose the basis of $T_yM$
by Gauss's Lemma. Recalling that the curvature operator is self-adjoint by page 36 of [Reference Pedersen13], we choose the basis of $T_yM$![]() so that the first basis vector points along the direction of the geodesic $\gamma _\tau (0)$
so that the first basis vector points along the direction of the geodesic $\gamma _\tau (0)$![]() . Hence Jacobi's equation (2.8) can be expressed as a second-order differential equation in block matrix form, with a symmetric matrix $S_{-\nabla (-\tau \psi )^c(y)}$
. Hence Jacobi's equation (2.8) can be expressed as a second-order differential equation in block matrix form, with a symmetric matrix $S_{-\nabla (-\tau \psi )^c(y)}$![]() given by components of the curvature tensor such that
given by components of the curvature tensor such that

as in (2.4) of [Reference Cordero-Erausquin, McCann and Schmuckensläger6]. Then the Jacobi equation reduces to a first-order block matrix equation with blocks of shape $(1+(n-1))\times (1+(n-1))$![]() in a $(2n)\times (2n)$
in a $(2n)\times (2n)$![]() matrix
matrix

To find the limit as $\tau \rightarrow 0$![]() , we can assume that $S_{-\nabla (-\tau \psi )^c (y)}$
, we can assume that $S_{-\nabla (-\tau \psi )^c (y)}$![]() is constant on the geodesic, and may be expressed as $\tau ^2 S$
is constant on the geodesic, and may be expressed as $\tau ^2 S$![]() where $\tau ^2 S=S_{\tau \nabla \psi (x)}$
where $\tau ^2 S=S_{\tau \nabla \psi (x)}$![]() has shape ${(n-1)\times (n-1)}$
has shape ${(n-1)\times (n-1)}$![]() . The functions $\cos \alpha$
. The functions $\cos \alpha$![]() and $\sin \alpha /\alpha$
and $\sin \alpha /\alpha$![]() are entire and even, so $\cos \sqrt {s}$
are entire and even, so $\cos \sqrt {s}$![]() and $\sin \sqrt {s}/\sqrt {s}$
and $\sin \sqrt {s}/\sqrt {s}$![]() are entire functions, hence they operate on complex matrices. Note that the matrix
are entire functions, hence they operate on complex matrices. Note that the matrix
in the bottom left corner is symmetric, has rank less than or equal to $n-1$![]() , and does not depend upon $t$
, and does not depend upon $t$![]() . Hence we consider the matrix
. Hence we consider the matrix

which has derivative

so we can use this formula to solve (2.18). So the approximate differential equation has solution

Hence by (2.9) we have

which gives rise to the approximation

and likewise we obtain
From (2.19), we have
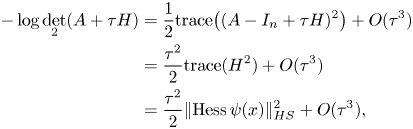
so the result follows by lemma 2.1.
We conclude with a transportation inequality which generalizes proposition 1.3 to the unit spheres ${\bf S}^n$![]() . See [Reference Blower and Bolley2] for a discussion of measures on product spaces.
. See [Reference Blower and Bolley2] for a discussion of measures on product spaces.
Theorem 2.3 Let $M={\bf S}^n$![]() for some $n\geq 2,$
for some $n\geq 2,$![]() and suppose that
and suppose that
for some $\kappa _U>0$![]() . Then
. Then
Proof. In this case, the curvature operator is constant, so we have $S_{\nabla \psi (x)} Y=\Vert \nabla \psi (x)\Vert ^2Y$![]() , so
, so
Thus the result follows with a similar proof to proposition 1.3 using data from the proof of proposition 2.2.
Acknowledgments
I thank Graham Jameson for helpful remarks concerning inequalities which led to (1.34). I am also grateful to the referee, whose helpful comments improved the exposition.