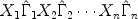Original Paper
Logistic Latent Trait Models with Linear Constraints
-
- Published online by Cambridge University Press:
- 01 January 2025, pp. 3-26
-
- Article
- Export citation
Some Contributions to Efficient Statistics in Structural Models: Specification and Estimation of Moment Structures
-
- Published online by Cambridge University Press:
- 01 January 2025, pp. 493-517
-
- Article
- Export citation
A Second Generation Nonlinear Factor Analysis
-
- Published online by Cambridge University Press:
- 01 January 2025, pp. 315-342
-
- Article
- Export citation
Indclus: An Individual differences Generalization of the Adclus Model and the Mapclus Algorithm
-
- Published online by Cambridge University Press:
- 01 January 2025, pp. 157-169
-
- Article
- Export citation
A Generalization of Kristof's Theorem on the Trace of Certain Matrix Products
-
- Published online by Cambridge University Press:
- 01 January 2025, pp. 519-523
-
- Article
- Export citation
Probabilistic Multidimensional Scaling: Complete and Incomplete Data
-
- Published online by Cambridge University Press:
- 01 January 2025, pp. 27-48
-
- Article
- Export citation
Orthogonal Procrustes Rotation Maximizing Congruence
-
- Published online by Cambridge University Press:
- 01 January 2025, pp. 343-352
-
- Article
- Export citation
Empirical Bayes Estimation of Coefficients in the General Linear Model from Data of Deficient Rank
-
- Published online by Cambridge University Press:
- 01 January 2025, pp. 171-181
-
- Article
- Export citation
A More Powerful Method for Testing for Agreement between a Judge and a known Standard
-
- Published online by Cambridge University Press:
- 01 January 2025, pp. 183-193
-
- Article
- Export citation
Some Improved Diagnostics for Failure of the Rasch Model
-
- Published online by Cambridge University Press:
- 01 January 2025, pp. 49-72
-
- Article
- Export citation
Best Linear Prediction of Composite Universe Scores
-
- Published online by Cambridge University Press:
- 01 January 2025, pp. 525-539
-
- Article
- Export citation
Tau-Equivalence and Equipercentile Equating
-
- Published online by Cambridge University Press:
- 01 January 2025, pp. 353-369
-
- Article
- Export citation
On Green's Best Linear Composites with a Specified Structure, and Oblique Estimates of Factor Scores
-
- Published online by Cambridge University Press:
- 01 January 2025, pp. 371-375
-
- Article
- Export citation
Evaluating Performance in Continuous Experiments with Feedback to Subjects
-
- Published online by Cambridge University Press:
- 01 January 2025, pp. 195-209
-
- Article
- Export citation
Some Types of Clustering with Relational Constraints
-
- Published online by Cambridge University Press:
- 01 January 2025, pp. 541-552
-
- Article
- Export citation
Parameterizing Inequality Constraints on Unique Variances in Linear Structural Models
-
- Published online by Cambridge University Press:
- 01 January 2025, pp. 73-83
-
- Article
- Export citation
A Maximum Likelihood Method for Fitting the Wandering Vector Model
-
- Published online by Cambridge University Press:
- 01 January 2025, pp. 553-566
-
- Article
- Export citation
An Approximation of the K out N Reliability of a Test, and a Scoring Procedure for Determining which Items an Examinee Knows
-
- Published online by Cambridge University Press:
- 01 January 2025, pp. 211-222
-
- Article
- Export citation
A General Framework for using Latent Class Analysis to Test Hierarchical and Nonhierarchical Learning Models
-
- Published online by Cambridge University Press:
- 01 January 2025, pp. 85-97
-
- Article
- Export citation
Alternative Weights and Invariant Parameters in Optimal Scaling
-
- Published online by Cambridge University Press:
- 01 January 2025, pp. 377-391
-
- Article
- Export citation