Hostname: page-component-5f745c7db-szhh2 Total loading time: 0 Render date: 2025-01-06T06:58:17.024Z Has data issue: true hasContentIssue false
  • English
  • Français

Latent Variable Selection for Multidimensional Item Response Theory Models via L1 Regularization

Published online by Cambridge University Press:  01 January 2025

Jianan Sun ,
Yunxiao Chen ,
Jingchen Liu ,
Zhiliang Ying  and
Tao Xin
Jianan Sun
Affiliation:
Beijing Forestry University
Yunxiao Chen
Affiliation:
Emory University
Jingchen Liu*
Affiliation:
Columbia University
Zhiliang Ying
Affiliation:
Columbia University
Tao Xin
Affiliation:
Beijing Normal University
*
Correspondence should be made to Jingchen Liu, Columbia University, New York, USA. Email: jcliu@stat.columbia.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We develop a latent variable selection method for multidimensional item response theory models. The proposed method identifies latent traits probed by items of a multidimensional test. 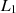Its basic strategy is to impose an L1\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$L_{1}$$\end{document} penalty term to the log-likelihood. The computation is carried out by the expectation–maximization algorithm combined with the coordinate descent algorithm. Simulation studies show that the resulting estimator provides an effective way in correctly identifying the latent structures. The method is applied to a real dataset involving the Eysenck Personality Questionnaire.

Keywords

latent variable selectionmultidimensional item response theory modelL1 regularizationexpectation–maximizationBIC
Type
Article
Information
Psychometrika , Volume 81 , Issue 4 , December 2016 , pp. 921 - 939
Copyright
Copyright © 2016 The Psychometric Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ackerman, T. A. (1989). Unidimensional IRT calibration of compensatory and noncompensatory multidimensional items. Applied Psychological Measurement, 13, 113–127.CrossRefGoogle Scholar
Ackerman, T. A. (1994). Using multidimensional item response theory to understand what items and tests are measuring. Applied Measurement in Education, 7, 255–278.CrossRefGoogle Scholar
Akaike, H. (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19, 716–723.CrossRefGoogle Scholar
Ansley, T. N., Forsyth, R. A. (1985). An examination of the characteristics of unidimensional IRT parameter estimates derived from two-dimensional data. Applied Psychological Measurement, 9, 37–48.CrossRefGoogle Scholar
Béguin, A. A., Glas, C. A. (2001). MCMC estimation and some model-fit analysis of multidimensional IRT models. Psychometrika, 66, 541–561.CrossRefGoogle Scholar
Bock, D. R., Gibbons, R., Muraki, E. (1988). Full-information item factor analysis. Applied Psychological Measurement, 12, 261–280.CrossRefGoogle Scholar
Bock, D. R., Gibbons, R., Schilling, S., Muraki, E., Wilson, D., & Wood, R. (2003). Testfact 4.0. In Computer software and manual. Lincolnwood, IL: Scientific Software International.Google Scholar
Bolt, D. M., Lall, V. F. (2003). Estimation of compensatory and noncompensatory multidimensional item response models using Markov chain Monte Carlo. Applied Psychological Measurement, 27, 395–414.CrossRefGoogle Scholar
Cai, L. (2010). High-dimensional exploratory item factor analysis by a Metropolis–Hastings Robbins–Monro algorithm. Psychometrika, 75, 33–57.CrossRefGoogle Scholar
Dempster, A. P., Laird, N. M., Rubin, D. B. (1977). Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society, Series B (Methodological), 39, 1–38.CrossRefGoogle Scholar
Donoho, D. L., Johnstone, I. M. (1995). Adapting to unknown smoothness via wavelet shrinkage. Journal of the American Statistical Association, 90, 1200–1224.CrossRefGoogle Scholar
Embretson, S. E. (1984). (2000). A general latent trait model for response processes. Psychometrika, 49, 175–186.CrossRefGoogle Scholar
Embretson, S. E., Reise, S. P. Psychometric methods: Item response theory for psychologists, Mahwah, NJ: Lawrence Erlbaum AssociatesGoogle Scholar
Eysenck, S., Barrett, P. (2013). Re-introduction to cross-cultural studies of the EPQ. Personality and Individual Differences, 54 (4), 485–489.CrossRefGoogle Scholar
Fraser, C., McDonald, R. P. (1988). NOHARM: Least squares item factor analysis. Multivariate Behavioral Research, 23, 267–269.CrossRefGoogle ScholarPubMed
Friedman, J., Hastie, T., Hofling, H., Tibshirani, R. (2007). Pathwise coordinate optimization. The Annals of Applied Statistics, 1, 302–332.CrossRefGoogle Scholar
Friedman, J., Hastie, T., Tibshirani, R. (2010). Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software, 33, 1CrossRefGoogle ScholarPubMed
Jöreskog, K. G. (1969). (2006). (1968). A general approach to confirmatory maximum likelihood factor analysis. Psychometrika, 34, 183–202.CrossRefGoogle Scholar
Kang, T. Model selection methods for unidimensional and multidimensional IRT models, Madison, WI: University of Wisconsin.Google Scholar
Lord, F. M., Novick, M. R. Statistical theories of mental test scores, Reading, MA: Addison-Wesley.Google Scholar
Mallows, C. L. (1973). Some comments on Cp. Technometrics, 15, 661–675.Google Scholar
Maydeu-Olivares, A., Liu, Y. (2015). Item diagnostics in multivariate discrete data. Psychological Methods, 20, 276–292.CrossRefGoogle ScholarPubMed
McDonald, R. P. (1967). Nonlinear factor analysis. Psychometric Monographs, No. 15. Richmond, VA: Psychometric Corporation.Google Scholar
McDonald, R. P. (1982). Linear versus nonlinear models in item response theory. Applied Psychological Measurement, 6, 379–396.CrossRefGoogle Scholar
McKinley, R. L. (1989). Confirmatory analysis of test structure using multidimensional item response theory. Technical Report No. RR-89-31. Princeton, NJ: Educational Testing Service.Google Scholar
McKinley, R. L., & Reckase, M. D. (1982). The use of the general Rasch model with multidimensional item response data. Technical Report No. ONR-82-1. Iowa City, IA: American College Testing Program.Google Scholar
Reckase, M. D. (1972). Development and application of a multivariate logistic latent trait model. Unpublished Doctoral Dissertation, Syracuse University, Syracuse, NY.Google Scholar
Reckase, M. D. (1997). (2009). The past and future of multidimensional item response theory. Applied Psychological Measurement, 21, 25–36.CrossRefGoogle Scholar
Reckase, M. D. Multidimensional item response theory, New York: Springer.CrossRefGoogle Scholar
Schwarz, G. (1978). Estimating the dimension of a model. The Annals of Statistics, 6, 461–464.CrossRefGoogle Scholar
Spiegelhalter, D. J., Best, N. G., Carlin, B. P., Van Der Linde, A. (2002). Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 64, 583–639.CrossRefGoogle Scholar
Svetina, D., Levy, R. (2012). An overview of software for conducting dimensionality assessment in multidimensional models. Applied Psychological Measurement, 36, 659–669.CrossRefGoogle Scholar
Sympson, J. B. (1978). A model for testing with multidimensional items. In D. J. Weiss (Ed.), Proceedings of the 1977 computerized adaptive testing conference (pp. 82–98).Google Scholar
Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Methodological), 58, 267–288.CrossRefGoogle Scholar
Way, W. D., Ansley, T. N., Forsyth, R. A. (1988). The comparative effects of compensatory and noncompensatory two-dimensional data on unidimensional IRT estimates. Applied Psychological Measurement, 12, 239–252.CrossRefGoogle Scholar