Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T20:44:52.105Z Has data issue: false hasContentIssue false
  • English
  • Français

Subharmonic solutions of a nonconvex noncoercive Hamiltonian system

Published online by Cambridge University Press:  15 April 2004

Najeh Kallel  and
Mohsen Timoumi
Najeh Kallel
Affiliation:
Institut préparatoire des Études d'ingénieurs de Sfax, Département de Mathématiques, BP 805, CP 3018, Tunisia.
Mohsen Timoumi
Affiliation:
Faculté des sciences de Monastir, Département de Mathématiques, CP 5000, Tunisia; m_timoumi@yahoo.com.
Get access

Abstract

In this paper we study the existence of subharmonic solutions of the Hamiltonian system $$ J\dot x+ u^* \nabla G(t,u(x)) =e(t)$$ 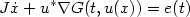where u is a linear map, G is a C 1-function and e is a continuous function.

Type
Research Article
Information
RAIRO - Operations Research , Volume 38 , Issue 1 , January 2004 , pp. 27 - 37
Copyright
© EDP Sciences, 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Conley, C. and Zehnder, E., Subharmonic solutions and Morse theory. Phys. A 124 (1984) 649-658. CrossRef
Ekeland, I. and Hofer, H., Subharmonics for convex nonautonomous Hamiltonian systems. Commun. Pure Appl. Math. 40 (1987) 1-36. CrossRef
Fonda, A. and Lazer, A.C., Subharmonic solutions of conservative systems with nonconvex potentials. Proc. Am. Math. Soc. 115 (1992) 183-190. CrossRef
F. Fonda and M. Willem, Subharmonic oscllations of forced pendulum-type equation J. Differ. Equations 81 (1989) 215-220.
Fournier, G., Timoumi, M. and Willem, M., The limiting case for strongly indefinite functionals. Topol. Meth. Nonlinear Anal. 1 (1993) 203-209. CrossRef
Giannoni, F., Periodic Solutions of Dynamical Systems by a Saddle Point Theorem of Rabinowitz. Nonlinear Anal. 13 (1989) 707-7019. CrossRef
Rabinowitz, P.H., Subharmonic Solutions, On of Hamiltonian Systems. Commun. Pure Appl. Math. 33 (1980) 609-633. CrossRef
Timoumi, M., Subharmonics of convex noncoercive Hamiltonian systems. Coll. Math. 43 (1992) 63-69.
Willem, M., Subharmonic oscillations of convex Hamiltonian systems. Nonlinear Anal. 9 (1985) 1311.