Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T01:54:02.041Z Has data issue: false hasContentIssue false
  • English
  • Français

Computing the prefix of an automaton

Published online by Cambridge University Press:  15 April 2002

Marie-Pierre Béal  and
Olivier Carton
Marie-Pierre Béal
Affiliation:
Institut Gaspard Monge, Université de Marne-la-Vallée, 5 boulevard Descartes, 77454 Marne-la-Vallée Cedex 2, France; (Marie-Pierre.Beal@univ-mlv.fr)
Olivier Carton
Affiliation:
Institut Gaspard Monge, Université de Marne-la-Vallée, 5 boulevard Descartes, 77454 Marne-la-Vallée Cedex 2, France; (Olivier.Carton@univ-mlv.f et url: http://www-igm.univ-mlv.fr/~beal/)
Get access

Abstract

We present an algorithm for computing the prefix of an automaton. Automata considered are non-deterministic, labelled on words, and can have ε-transitions. The prefix automaton of an automaton $\mathcal{A}$ 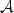has the following characteristic properties. It has the same graph as $\mathcal{A}$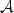. Each accepting path has the same label as in $\mathcal{A}$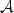. For each state q, the longest common prefix of the labels of all paths going from q to an initial or final state is empty. The interest of the computation of the prefix of an automaton is that it is the first step of the minimization of sequential transducers. The algorithm that we describe has the same worst case time complexity as another algorithm due to Mohri but our algorithm allows automata that have empty labelled cycles. If we denote by P(q) the longest common prefix of labels of paths going from q to an initial or final state, it operates in time O((P+1) × |E|) where P is the maximal length of all P(q).

Keywords

Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 34 , Issue 6 , November 2000 , pp. 503 - 514
Copyright
© EDP Sciences, 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

A.V. Aho, J.E. Hopcroft and J.D. Ullman, The Design and Analysis of Computer Algorithms. Addison Wesley (1974).
M.-P. Béal, Codage Symbolique. Masson (1993).
M.-P. Béal and O. Carton, Determinization of transducers over finite and infinite words. Tech. Rep. 99-12, I.G.M., Université de Marne-la-Vallée (1999).
J. Berstel, Transductions and Context-Free Languages. B.G. Teubner (1979).
Breslauer, D., The suffix tree of a tree and minimizing sequential transducers, in CPM'96. Springer-Verlag, Lecture Notes in Comput. Sci. 1075 (1996) 116-129. CrossRef
Breslauer, D., The suffix tree of a tree and minimizing sequential transducers. Theoret. Comput. Sci. 191 (1998) 131-144. CrossRef
C. Choffrut, Contribution à l'étude de quelques familles remarquables de fonctions rationnelles. Thèse d'État, Université Paris VII (1978).
Choffrut, C., A generalization of Ginsburg and Rose's characterization of gsm mappings, in ICALP'79. Springer-Verlag, Lecture Notes in Comput. Sci. 71 (1979) 88-103. CrossRef
T.H. Cormen, C.E. Leiserson and R.L. Rivest, Introduction to Algorithms. MIT Press (1990).
M. Crochemore, C. Hancart and T. Lecroq, Algorithmique du Texte. Vuibert (to appear).
C. Frougny, Numeration systems, in Algebraic Combinatorics on Words, edited by M. Lothaire. Cambridge (to appear).
Mohri, M., Minimization of sequential transducers, in CPM'94, edited by M. Crochemore and D. Gusfield. Springer-Verlag, Lecture Notes in Comput. Sci. 807 (1994) 151-163. CrossRef
Mohri, M., Minimization algorithms for sequential transducers. Theoret. Comput. Sci. 234 (2000) 177-201. CrossRef
E. Roche and Y. Schabes, Finite-State Language Processing. MIT Press, Cambridge (1997) Chapter 7.