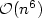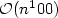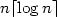Refine listing
Actions for selected content:
Contents
Research Article
Finite presentabilityof strongly finite dilators
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 425-431
-
- Article
- Export citation
Domain-Free λµ-Calculus
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 433-466
-
- Article
- Export citation
Two-variable word equations
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 467-501
-
- Article
- Export citation
Computing the prefix of an automaton
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 503-514
-
- Article
- Export citation
Cutwidth of the r-dimensional Mesh of d-ary Trees
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 515-519
-
- Article
- Export citation
Galois Lattice as a Framework to Specify Building Class Hierarchies Algorithms
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 521-548
-
- Article
- Export citation
A Compositional Approach to Synchronize Two Dimensional Networks of Processors
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 549-564
-
- Article
- Export citation
Characteristic Formulaefor Timed Automata
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 565-584
-
- Article
- Export citation
Codes générateurs minimaux de langagesde mots bi-infinis
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 585-596
-
- Article
- Export citation