Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T02:17:10.067Z Has data issue: false hasContentIssue false
  • English
  • Français

Two-variable word equations

Published online by Cambridge University Press:  15 April 2002

Lucian Ilie  and
Wojciech Plandowski
Lucian Ilie
Affiliation:
Department of Computer Science, University of Western Ontario, N6A 5B7, London, Ontario, Canada; (ilie@csd.uwo.ca)
Wojciech Plandowski
Affiliation:
Turku Centre for Computer Science TUCS, 20520 Turku, Finland; and Institute of Informatics, University of Warsaw, Banacha 2, 02-097, Warsaw, Poland; (wojtekpl@mimuw.edu.pl)
Get access

Abstract

We consider languages expressed by word equations in two variables and give a complete characterization for their complexity functions, that is, the functions that give the number of words of the same length. Specifically, we prove that there are only five types of complexities: constant, linear, exponential, and two in between constant and linear. For the latter two, we give precise characterizations in terms of the number of solutions of Diophantine equations of certain types. In particular, we show that the linear upper bound on the non-exponential complexities by Karhumäki et al. in [9], is tight. There are several consequences of our study. First, we derive that both of the sets of all finite Sturmian words and of all finite Standard words are expressible by word equations. Second, we characterize the languages of non-exponential complexity which are expressible by two-variable word equations as finite unions of several simple parametric formulae and solutions of a two-variable word equation with a finite graph. Third, we find optimal upper bounds on the solutions of (solvable) two-variable word equations, namely, linear bound for one variable and quadratric for the other. From this, we obtain an $\mathcal{O}(n^6)$ 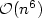algorithm for testing the solvability of two-variable word equations, improving thus very much Charatonik and Pacholski's $\mathcal{O}(n^100)$ 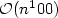algorithm from [3].

Keywords

Word equationexpressible languagecomplexity functionminimal solutionsolvability.
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 34 , Issue 6 , November 2000 , pp. 467 - 501
Copyright
© EDP Sciences, 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Angluin, D., Finding patterns common to a set of strings. J. Comput. System Sci. 21 (1980) 46-62. CrossRef
J. Berstel, Recent results in Sturmian words, edited by J. Dassow, G. Rozenberg and A. Salomaa, Developments in Language Theory II, World Sci. Publishing (1996) 13-24.
Charatonik, W. and Pacholski, L., Word equations with two variables, in Proc. of IWWERT'91, edited by H. Abdulrab and J.P. Pecuchet. Springer, Berlin, Lecture Notes in Comput. Sci. 667 (1991) 43-57.
C. Choffrut and J. Karhumäki, Combinatorics of words, edited by G. Rozenberg and A. Salomaa, Handbook of Formal Languages. Springer, Berlin (1997) 329-438.
de Luca, A. and Mignosi, F., Some combinatorial properties of sturmian words. Theoret. Comput. Sci. 136 (1994) 361-385. CrossRef
Eyono Obono, S., Goralcik, P. and Maksimenko, M., Efficient solving of the word equations in one variable, in Proc. of MFCS'94. Springer, Berlin, Lecture Notes in Comput. Sci. 841 (1994) 336-341. CrossRef
Yu.I. Hmelevskii, Equations in free semigroups. Trudy Mat. Inst. Steklov 107 (1971). English transl. Proc Steklov Inst. of Mathematics 107 (1971). Amer. Math. Soc. (1976).
Jiang, T., Salomaa, A., Salomaa, K. and Decision, S. Yu problems for patterns. J. Comput. System Sci. 50 (1995) 53-63. CrossRef
Karhumäki, J., Mignosi, F. and Plandowski, W., The expressibility of languages and relations by word equations, in Proc. of ICALP'97. Springer, Berlin, Lecture Notes in Comput. Sci. 1256 (1997) 98-109. CrossRef
Koscielski, A. and Pacholski, L., Complexity of Makanin's algorithm. J. ACM 43 (1996) 670-684. CrossRef
M. Lothaire, Combinatorics on Words. Addison-Wesley, Reading, MA (1983).
Makanin, G.S., The problem of solvability of equations in a free semigroup. Mat. Sb. 103 (1977) 147-233. English transl. in Math. U.S.S.R. Sb. 32 (1977).
G. Rauzy, Mots infinis en arithmetique, edited by M. Nivat and D. Perrin, Automata on infinite words. Springer, Berlin, Lecture Notes in Comput. Sci. 192 (1984).
Razborov, A., On systems of equations in a free group. Math. USSR Izvestija 25 (1985) 115-162. CrossRef
A. Razborov, On systems of equations in a free group. Ph.D. Thesis, Moscow State University (1987).
W. Sierpinski, Elementary Theory of Numbers. Elseviers Science Publishers B.V., Amsterdam, and PWN - Polish Scientific Publishers, Warszawa (1988).