Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T20:01:33.619Z Has data issue: false hasContentIssue false
  • English
  • Français

THE PERIPATETIC PROGRAM IN CATEGORICAL LOGIC: LEIBNIZ ON PROPOSITIONAL TERMS

Published online by Cambridge University Press:  06 November 2018

MARKO MALINK  and
ANUBAV VASUDEVAN
MARKO MALINK*
Affiliation:
Department of Philosophy, New York University
ANUBAV VASUDEVAN*
Affiliation:
Department of Philosophy, University of Chicago
*
*DEPARTMENT OF PHILOSOPHY NEW YORK UNIVERSITY 5 WASHINGTON PLACE NEW YORK, NY 10003, USA E-mail: mm7761@nyu.edu
†DEPARTMENT OF PHILOSOPHY UNIVERSITY OF CHICAGO 1115 EAST 58th STREET CHICAGO, IL 60637, USA E-mail: anubav@uchicago.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Greek antiquity saw the development of two distinct systems of logic: Aristotle’s theory of the categorical syllogism and the Stoic theory of the hypothetical syllogism. Some ancient logicians argued that hypothetical syllogistic is more fundamental than categorical syllogistic on the grounds that the latter relies on modes of propositional reasoning such as reductio ad absurdum. Peripatetic logicians, by contrast, sought to establish the priority of categorical over hypothetical syllogistic by reducing various modes of propositional reasoning to categorical form. In the 17th century, this Peripatetic program of reducing hypothetical to categorical logic was championed by Gottfried Wilhelm Leibniz. In an essay titled Specimina calculi rationalis, Leibniz develops a theory of propositional terms that allows him to derive the rule of reductio ad absurdum in a purely categorical calculus in which every proposition is of the form A is B. We reconstruct Leibniz’s categorical calculus and show that it is strong enough to establish not only the rule of reductio ad absurdum, but all the laws of classical propositional logic. Moreover, we show that the propositional logic generated by the nonmonotonic variant of Leibniz’s categorical calculus is a natural system of relevance logic known as RMI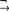$_{{}_ \to ^\neg }$.

Keywords

01A2001A4503A0503B0503B47LeibnizAristotlecategorical syllogismhypothetical syllogismreductio ad absurdumrelevance logic
Type
Research Article
Information
The Review of Symbolic Logic , Volume 13 , Issue 1 , March 2020 , pp. 141 - 205
Copyright
Copyright © Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Ackrill, J. L. (1963). Aristotle’s Categories and De Interpretatione. Oxford: Clarendon Press.CrossRefGoogle Scholar
Adams, R. M. (1994). Leibniz: Determinist, Theist, Idealist. New York: Oxford University Press.Google Scholar
Ahmed, A. Q. (2011). Avicenna’s Deliverance: Logic. Oxford: Oxford University Press.Google Scholar
Aldrich, H. (1691). Artis Logicae Compendium. Oxford: Sheldonian Theatre.Google Scholar
Alsted, J. H. (1628). Logicae Systema Harmonicum (second edition). Herborn: Corvinus.Google Scholar
Alsted, J. H. (1630). Encyclopaedia Septem Tomis Distincta. Herborn: Corvinus.Google Scholar
Angell, R. B. (1986). Truth-functional conditionals and modern vs. traditional syllogistic. Mind, 95, 210–223.CrossRefGoogle Scholar
Ashworth, E. J. (1968). Propositional logic in the sixteenth and early seventeenth centuries. Notre Dame Journal of Formal Logic, 9, 179–192.CrossRefGoogle Scholar
Avron, A. (1984). Relevant entailment: Semantics and formal systems. Journal of Symbolic Logic, 49, 334–342.CrossRefGoogle Scholar
Avron, A. (2016). RM and its nice properties. In Bimbó, K., editor. J. Michael Dunn on Information Based Logics. Basel: Springer, pp. 15–43.CrossRefGoogle Scholar
Barnes, J. (1980). Proof destroyed. In Schofield, M., Burnyeat, M. F., and Barnes, J., editors. Doubt and Dogmatism: Studies in Hellenistic Epistemology. Oxford: Clarendon Press, pp. 161–181.Google Scholar
Barnes, J. (1983). Terms and sentences: Theophrastus on hypothetical syllogisms. Proceedings of the British Academy, 69, 279–326.Google Scholar
Barnes, J. (1985). Theophrastus and hypothetical syllogistic. In Wiesner, J., editor. Aristoteles: Werk und Wirkung. Band 1: Aristoteles und seine Schule. Berlin: de Gruyter, pp. 557–576.Google Scholar
Barnes, J. (1990). Logical form and logical matter. In Alberti, A., editor. Logica, Mente e Persona. Florence: Olschki, pp. 7–119.Google Scholar
Barnes, J. (1993). Aristotle’s Posterior Analytics (second edition). Oxford: Clarendon Press.Google Scholar
Barnes, J. (1999). Logic: The Peripatetics. In Algra, K., Barnes, J., Mansfeld, J., and Schofield, M., editors. The Cambridge History of Hellenistic Philosophy. Cambridge: Cambridge University Press, pp. 77–83.CrossRefGoogle Scholar
Barnes, J. (2007). Truth, etc.: Six Lectures on Ancient Logic. Oxford: Clarendon Press.Google Scholar
Barnes, J. (2012). Logical Matters: Essays in Ancient Philosophy II. Oxford: Clarendon Press.Google Scholar
Bassler, O. B. (1998). Leibniz on intension, extension, and the representation of syllogistic inference. Synthese, 116, 117–139.CrossRefGoogle Scholar
Bobzien, S. (1996). Stoic syllogistic. Oxford Studies in Ancient Philosophy, 14, 133–192.Google Scholar
Bobzien, S. (1997). The Stoics on hypotheses and hypothetical arguments. Phronesis, 42, 299–312.CrossRefGoogle Scholar
Bobzien, S. (2000). Wholly hypothetical syllogisms. Phronesis, 45, 87–137.CrossRefGoogle Scholar
Bobzien, S. (2002a). The development of modus ponens in antiquity: From Aristotle to the 2nd century AD. Phronesis, 47, 359–394.CrossRefGoogle Scholar
Bobzien, S. (2002b). Some elements of propositional logic in Ammonius. In Linneweber-Lammerskitten, H. and Mohr, G., editors. Interpretation und Argument. Würzburg: Königshausen & Neumann, pp. 103–119.Google Scholar
Bobzien, S. (2002c). Pre-Stoic hypothetical syllogistic in Galen’s Institutio logica. In Nutton, V., editor, The Unknown Galen: Bulletin of the Institute of Classical Studies, Suppl. 77 . London: Wiley, pp. 57–72.Google Scholar
Bobzien, S. (2004). Peripatetic hypothetical syllogistic in Galen—Propositional logic off the rails? Rhizai, 2, 57–102.Google Scholar
Bolton, R. (1994). The problem of dialectical reasoning (συλλογισμός) in Aristotle. Ancient Philosophy, 14, 99–132.CrossRefGoogle Scholar
Boole, G. (1847). The Mathematical Analysis of Logic, Being an Essay Towards a Calculus of Deductive Reasoning. Cambridge: Macmillan.Google Scholar
Boole, G. (1854). An Investigation of the Laws of Thought, on Which Are Founded the Mathematical Theories of Logic and Probabilities. London: Walton and Maberley.Google Scholar
Boole, G. (1952). Studies in Logic and Probability. London: Watts & Co.Google Scholar
Brady, G. (1997). From the algebra of relations to the logic of quantifiers. In Houser, N., Roberts, D. D., and van Evra, J., editors. Studies in the Logic of Charles Sanders Peirce. Bloomington and Indianapolis: Indiana University Press, pp. 173–191.Google Scholar
Byrne, P. H. (1997). Analysis and Science in Aristotle. Albany: State University of New York Press.Google Scholar
Castagnoli, L. (2016). Aristotle on the non-cause fallacy. History and Philosophy of Logic, 37, 9–32.CrossRefGoogle Scholar
Castañeda, H.-N. (1990). Leibniz’s complete propositional logic. Topoi, 9, 15–28.CrossRefGoogle Scholar
Charles, D. (2000). Aristotle on Meaning and Essence. Oxford: Clarendon Press.Google Scholar
Coope, U. (2005). Time for Aristotle: Physics IV.10–14. Oxford: Clarendon Press.CrossRefGoogle Scholar
Corcoran, J. (1972). Completeness of an ancient logic. Journal of Symbolic Logic, 37, 696–702.CrossRefGoogle Scholar
Corcoran, J. (1974). Aristotle’s natural deduction system. In Corcoran, J., editor. Ancient Logic and its Modern Interpretations. Boston: Reidel, pp. 85–131.CrossRefGoogle Scholar
Corcoran, J. (2006). Schemata: The concept of schema in the history of logic. Bulletin of Symbolic Logic, 12, 219–240.CrossRefGoogle Scholar
Couturat, L. (1914). The Algebra of Logic. Chicago and London: Open Court.Google Scholar
Crellius, F. (1595). Isagoge Logica (fifth edition). Heidelberg: Harnisch.Google Scholar
Crivelli, P. (2004). Aristotle on Truth. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Crivelli, P. (2011). Aristotle on syllogisms from a hypothesis. In Longo, A., editor. Argument from Hypothesis in Ancient Philosophy. Naples: Bibliopolis, pp. 95–184.Google Scholar
Crubellier, M. (2014). Aristote: Premiers Analytiques. Paris: Flammarion.Google Scholar
De Morgan, A. (1847). Formal Logic or, the Calculus of Inference, Necessary and Probable. London: Taylor and Walton.Google Scholar
Dietericus, C. (1618). Institutiones Dialecticae (fifth edition). Giessen: Hampel.Google Scholar
Doull, F. A. (1991). Leibniz’s logical system of 1686–1690. Theoria, 6, 9–28.Google Scholar
Ebert, T. & Nortmann, U. (2007). Aristoteles: Analytica Priora, Buch I. Berlin: Akademie Verlag.CrossRefGoogle Scholar
Ebrey, D. (2015). Why are there no conditionals in Aristotle’s logic? Journal of the History of Philosophy, 53, 185–205.CrossRefGoogle Scholar
Frede, M. (1974). Stoic vs. Aristotelian syllogistic. Archiv für Geschichte der Philosophie, 56, 1–32.CrossRefGoogle Scholar
Frege, G. (1979). Posthumous Writings. Oxford: Blackwell.Google Scholar
Hailperin, T. (2004). Algebraical logic 1685–1900. In Gabbay, D. M. and Woods, J., editors. Handbook of the History of Logic, Volume 3. The Rise of Modern Logic: From Leibniz to Frege. Amsterdam: Elsevier, pp. 323–388.CrossRefGoogle Scholar
Helmig, C. (2017). Proclus on epistemology, language, and logic. In d’Hoine, P. and Martijn, M., editors. All from One: A Guide to Proclus. Oxford: Oxford University Press, pp. 183–206.Google Scholar
Hodges, W. (2017). Ibn Sīnā on reductio ad absurdum. Review of Symbolic Logic, 10, 583–601.CrossRefGoogle Scholar
Houser, N. (1990). The Schröder-Peirce correspondence. Modern Logic, 1, 206–236.Google Scholar
Ierodiakonou, K. (1996). The hypothetical syllogisms in the Greek and Latin traditions. Cahiers de l’Institut du Moyen-Âge Grec et Latin, 66, 96–116.Google Scholar
Ierodiakonou, K. (2016). A note on reductio ad impossibile in post-Aristotelian logic. In Gourinat, J.-B. and Lemaire, J., editors. Logique et dialectique dans l’Antiquité. Paris: Vrin, pp. 347–361.Google Scholar
Jenkinson, A. J. (1928). Aristotle’s Analytica Priora. In Ross, W. D., editor. The Works of Aristotle Translated into English, Vol. 1. Oxford: Clarendon Press.Google Scholar
Jungius, J. (1638). Logica Hamburgensis. Hamburg: Offermans.Google Scholar
Juniewicz, M. (1987). Leibniz’s modal calculus of concepts. In Srzednicki, J., editor. Initiatives in Logic. Dordrecht: Kluwer, pp. 36–51.CrossRefGoogle Scholar
Kauppi, R. (1960). Über die Leibnizsche Logik: Mit besonderer Berücksichtigung des Problems der Intension und der Extension. Helsinki: Suomalaisen Kirjallisuuden Kirjapaino.Google Scholar
Kühner, R. & Gerth, B. (1904). Ausführliche Grammatik der griechischen Sprache. Zweiter Teil: Satzlehre. Zweiter Band (third edition). Hannover and Leipzig: Hahn.Google Scholar
Ladd Franklin, C. (1892). Review of E. Schröder, Vorlesungen über die Algebra der Logik. Mind, 1, 126–132.Google Scholar
Lear, J. (1980). Aristotle and Logical Theory. Cambridge: Cambridge University Press.Google Scholar
Lenzen, W. (1983). Zur extensionalen und “intensionalen” Interpretation der Leibnizschen Logik. Studia Leibnitiana, 15, 129–148.Google Scholar
Lenzen, W. (1984a). “Unbestimmte Begriffe” bei Leibniz. Studia Leibnitiana, 16, 1–26.Google Scholar
Lenzen, W. (1984b). Leibniz und die Boolesche Algebra. Studia Leibnitiana, 16, 187–203.Google Scholar
Lenzen, W. (1986). ‘Non est’ non est ‘est non’. Zu Leibnizens Theorie der Negation. Studia Leibnitiana, 18, 1–37.Google Scholar
Lenzen, W. (1987). Leibniz’s calculus of strict implication. In Srzednicki, J., editor. Initiatives in Logic. Dordrecht: Kluwer, pp. 1–35.Google Scholar
Lenzen, W. (1988). Zur Einbettung der Syllogistik in Leibnizens ‘Allgemeinen Kalkül’. In Heinekamp, A., editor. Leibniz: Questions de logique. Stuttgart: Steiner Verlag, pp. 38–71.Google Scholar
Lenzen, W. (2000). Guilielmi Pacidii Non plus ultra, oder: Eine Rekonstruktion des Leibnizschen Plus-Minus-Kalküls. Logical Analysis and History of Philosophy, 3, 71–118.CrossRefGoogle Scholar
Lenzen, W. (2004). Leibniz’s logic. In Gabbay, D. M. and Woods, J., editors. Handbook of the History of Logic, Volume 3. The Rise of Modern Logic: From Leibniz to Frege. Amsterdam: Elsevier, pp. 1–83.Google Scholar
Londey, D. & Johanson, C. (1987). The Logic of Apuleius. Leiden: Brill.CrossRefGoogle Scholar
Łukasiewicz, J. (1935). Zur Geschichte der Aussagenlogik. Erkenntnis, 5, 111–131.CrossRefGoogle Scholar
Łukasiewicz, J. (1957). Aristotle’s Syllogistic from the Standpoint of Modern Formal Logic (second edition). Oxford: Clarendon Press.Google Scholar
Łukasiewicz, J. (1963). Elements of Mathematical Logic. Warsaw: Państwowe Wydawnictwo Naukowe.Google Scholar
Malink, M. (2013). Aristotle’s Modal Syllogistic. Cambridge, M.A.: Harvard University Press.CrossRefGoogle Scholar
Malink, M. & Vasudevan, A. (2016). The logic of Leibniz’s Generales inquisitiones de analysi notionum et veritatum. Review of Symbolic Logic, 9, 686–751.CrossRefGoogle Scholar
Malink, M. & Vasudevan, A. (2017). Leibniz’s theory of propositional terms: A reply to Massimo Mugnai. Leibniz Review, 27, 139–155.CrossRefGoogle Scholar
McCall, S. (1966). Connexive implication. Journal of Symbolic Logic, 31, 415–433.CrossRefGoogle Scholar
McCall, S. (1967). Connexive implication and the syllogism. Mind, 76, 346–356.CrossRefGoogle Scholar
McCall, S. (2012). A history of connexivity. In Gabbay, D. M., Pelletier, F. J., and Woods, J., editors. Handbook of the History of Logic, Volume 11. Logic: A History of its Central Concepts . Amsterdam: North-Holland, pp. 415–449.CrossRefGoogle Scholar
Mendell, H. (1998). Making sense of Aristotelian demonstration. Oxford Studies in Ancient Philosophy, 16, 161–225.Google Scholar
Menn, S. (2009). Aporiai 13–14. In Crubellier, M. and Laks, A., editors. Aristotle’s Metaphysics Beta: Symposium Aristotelicum. Oxford: Oxford University Press, pp. 211–266.Google Scholar
Moody, E. A. (1953). Truth and Consequence in Mediaeval Logic. Amsterdam: North-Holland.Google Scholar
Moss, L. (2011). Syllogistic logic with complements. In van Benthem, J., Gupta, A., and Pacuit, E., editors. Games, Norms and Reasons: Logic at the Crossroads. Dordrecht: Springer, pp. 179–197.CrossRefGoogle Scholar
Mueller, I. (1969). Stoic and Peripatetic logic. Archiv für Geschichte der Philosophie, 51, 173–187.CrossRefGoogle Scholar
Mugnai, M. (2017). Leibniz’s mereology in the essays on logical calculus of 1686–90. In Li, W., editor. Für unser Glück oder das Glück Anderer: Vorträge des X. Internationalen Leibniz-Kongresses, Vol. 6. Hildesheim: Olms, pp. 175–194.Google Scholar
Nambiar, S. (2000). The influence of Aristotelian logic on Boole’s philosophy of logic: The reduction of hypotheticals to categoricals. In Gasser, J., editor. A Boole Anthology: Recent and Classical Studies in the Logic of George Boole. Dordrecht: Springer, pp. 217–239.CrossRefGoogle Scholar
Nuchelmans, G. (1992). Secundum/Tertium Adiacens: Vicissitudes of a Logical Distinction. Amsterdam: Noord-Hollandsche.Google Scholar
Owen, O. F. (1889). The Organon, or Logical Treatises, of Aristotle, Vol. 1. London: Bell & Sons.Google Scholar
Pacius, J. (1597). In Porphyrii Isagogen et Aristotelis Organum Commentarius Analyticus. Frankfurt: Heredes Andreae Wecheli.Google Scholar
Panayides, C. Y. (1999). Aristotle on the priority of actuality in substance. Ancient Philosophy, 19, 327–344.CrossRefGoogle Scholar
Parkinson, G. H. R. (1965). Logic and Reality in Leibniz’s Metaphysics. Oxford: Clarendon Press.Google Scholar
Parkinson, G. H. R. (1966). Leibniz: Logical Papers. Oxford: Clarendon Press.Google Scholar
Parsons, T. (2014). Articulating Medieval Logic. Oxford: Oxford University Press.CrossRefGoogle Scholar
Patterson, R. (1995). Aristotle’s Modal Logic: Essence and Entailment in the Organon. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Patzig, G. (1968). Aristotle’s Theory of the Syllogism: A Logico-Philological Study of Book A of the Prior Analytics. Dordrecht: Reidel.CrossRefGoogle Scholar
Peckhaus, V. (1998). Hugh MacColl and the German algebra of logic. Nordic Journal of Philosophical Logic, 3, 17–34.Google Scholar
Peirce, C. S. (1873). Description of a notation for the logic of relatives, resulting from an amplification of the conceptions of Boole’s calculus of logic. Memoirs of the American Academy of Arts and Sciences, New Series, 9, 317–378.Google Scholar
Peirce, C. S. (1880). On the algebra of logic. American Journal of Mathematics, 3, 15–57.CrossRefGoogle Scholar
Peirce, C. S. (1885). On the algebra of logic: A contribution to the philosophy of notation. American Journal of Mathematics, 7, 180–196.CrossRefGoogle Scholar
Peramatzis, M. (2011). Priority in Aristotle’s Metaphysics. Oxford: Oxford University Press.CrossRefGoogle Scholar
Priest, G. (2006). Doubt Truth to Be a Liar. Oxford: Clarendon Press.Google Scholar
Priest, G. (2007). Paraconsistency and dialetheism. In Gabbay, D. M. and Woods, J., editors. Handbook of the History of Logic, Volume 8. The Many Valued and Nonmonotonic Turn in Logic. Amsterdam: North-Holland, pp. 129–204.CrossRefGoogle Scholar
Primavesi, O. (1996). Die Aristotelische Topik: Ein Interpretationsmodell und seine Erprobung am Beispiel von Topik B. München: Beck.Google Scholar
Prior, A. N. (1949). Categoricals and hypotheticals in George Boole and his successors. Australasian Journal of Philosophy, 27, 171–196.CrossRefGoogle Scholar
Prior, A. N. (1955). Formal Logic. Oxford: Clarendon Press.Google Scholar
Quine, W. V. (1986). Philosophy of Logic (second edition). Cambridge, M.A.: Harvard University Press.Google Scholar
Read, S. (2015). Aristotle and Łukasiewicz on existential import. Journal of the American Philosophical Association, 1, 535–544.CrossRefGoogle Scholar
Ross, W. D. (1949). Aristotle’s Prior and Posterior Analytics: A Revised Text with Introduction and Commentary. Oxford: Clarendon Press.CrossRefGoogle Scholar
Sánchez-Valencia, V. (2004). The algebra of logic. In Gabbay, D. M. and Woods, J., editors. Handbook of the History of Logic, Volume 3. The Rise of Modern Logic: From Leibniz to Frege. Amsterdam: Elsevier, pp. 389–544.CrossRefGoogle Scholar
Schröder, E. (1890). Vorlesungen über die Algebra der Logik. Erster Band. Leipzig: Teubner.Google Scholar
Schröder, E. (1891). Vorlesungen über die Algebra der Logik. Zweiter Band, erste Abteilung. Leipzig: Teubner.Google Scholar
Schröder, E. (1905). Vorlesungen über die Algebra der Logik. Zweiter Band, zweite Abteilung. Leipzig: Teubner.Google Scholar
Schupp, F. (1993). Gottfried Wilhelm Leibniz: Allgemeine Untersuchungen über die Analyse der Begriffe und Wahrheiten (second edition). Hamburg: Felix Meiner.Google Scholar
Schupp, F. (2000). Gottfried Wilhelm Leibniz: Die Grundlagen des logischen Kalküls. Hamburg: Felix Meiner.Google Scholar
Shehaby, N. (1973). The Propositional Logic of Avicenna: A Translation from al-Shifā’: al-Qiyās. Dordrecht: Reidel.CrossRefGoogle Scholar
Slomkowski, P. (1997). Aristotle’s Topics. Leiden: Brill.CrossRefGoogle Scholar
Smiley, T. J. (1973). What is a syllogism? Journal of Philosophical Logic, 2, 136–154.CrossRefGoogle Scholar
Smith, R. (1989). Aristotle’s Prior Analytics. Indianapolis: Hackett.Google Scholar
Smith, R. (1997). Aristotle’s Topics, Books I and VIII. Oxford: Clarendon Press.Google Scholar
Sommers, F. (1970). The calculus of terms. Mind, 79, 1–39.CrossRefGoogle Scholar
Sommers, F. (1982). The Logic of Natural Language. Oxford: Clarendon Press.Google Scholar
Sommers, F. (1993). The world, the facts, and primary logic. Notre Dame Journal of Formal Logic, 34, 169–182.CrossRefGoogle Scholar
Sommers, F. & Englebretsen, G. (2000). An Invitation to Formal Reasoning: The Logic of Terms. Aldershot: Ashgate.Google Scholar
Soreth, M. (1972). Zum infiniten Prädikat im zehnten Kapitel der Aristotelischen Hermeneutik. In Walzer, R., Stern, S. M., Hourani, A. H., and Brown, V., editors. Islamic Philosophy and the Classical Tradition. Columbia: University of South Carolina Press, pp. 389–424.Google Scholar
Speca, A. (2001). Hypothetical Syllogistic and Stoic Logic. Leiden: Brill.CrossRefGoogle Scholar
Street, T. (2004). Arabic logic. In Gabbay, D. M. and Woods, J., editors. Handbook of the History of Logic, Volume 1. Greek, Indian and Arabic Logic. Amsterdam: Elsevier, pp. 523–596.CrossRefGoogle Scholar
Striker, G. (2009). Aristotle’s Prior Analytics, Book I. Oxford: Clarendon Press.Google Scholar
Swoyer, C. (1995). Leibniz on intension and extension. Noûs, 29, 96–114.CrossRefGoogle Scholar
Tarski, A. (1956). Logic, Semantics, Metamathematics: Papers From 1923 to 1938. Oxford: Clarendon Press. Translated by Woodger, J. H..Google Scholar
Thom, P. (1981). The Syllogism. München: Philosophia.Google Scholar
Thompson, M. (1953). On Aristotle’s square of opposition. Philosophical Review, 62, 251–265.CrossRefGoogle Scholar
Tredennick, H. (1938). Aristotle’s Prior Analytics. Loeb Classical Library. Cambridge, M.A.: Harvard University Press.Google Scholar
van Rooij, R. (2012). The propositional and relational syllogistic. Logique et Analyse, 55, 85–108.Google Scholar
van Rooij, R. (2014). Leibnizian intensional semantics for syllogistic reasoning. In Ciuni, R., Wansing, H., and Willkommen, C., editors. Recent Trends in Philosophical Logic. Heidelberg: Springer, pp. 179–194.CrossRefGoogle Scholar
Vaught, R. L. (1967). Axiomatizability by a schema. Journal of Symbolic Logic, 32, 473–479.CrossRefGoogle Scholar
Venn, J. (1881). Symbolic Logic. London: Macmillan.CrossRefGoogle Scholar
von Kirchmann, J. H. (1877). Aristoteles’ erste Analytiken, oder: Lehre vom Schluss. Leipzig: Koschny.Google Scholar
Wallis, J. (1687). Institutio Logicae, ad Communes Usus Accommodata. Oxford: Sheldonian Theatre.Google Scholar
Wedin, M. V. (1990). Negation and quantification in Aristotle. History and Philosophy of Logic, 11, 131–150.CrossRefGoogle Scholar
Weidemann, H. (2004). Aristotle on the reducibility of all valid syllogistic moods to the two universal moods of the first figure (APr A7, 29b1–29b25). History and Philosophy of Logic, 25, 73–78.CrossRefGoogle Scholar
Weidemann, H. (2014). Aristoteles: Peri Hermeneias (third edition). Berlin: de Gruyter.Google Scholar
Whately, R. (1827). Elements of Logic (second edition). London: Mawman.Google Scholar
Whitaker, C. W. A. (1996). Aristotle’s De Interpretatione: Contradiction and Dialectic. Oxford: Oxford University Press.Google Scholar