The Scarr–Rowe effect is the apparent tendency of the heritability of IQ to be lower among those raised in families with lower socioeconomic status (SES). This effect might result from adverse bioecological conditions restricting the variance in opportunities among those with low SES, which in turn supresses the expression of IQ-related genetic variants during development via a gene × environment (G × E) interaction (Bronfenbrenner & Ceci, Reference Bronfenbrenner and Ceci1994). The effect was first described by Scarr-Salapatek (Reference Scarr-Salapatek1971) in a study of Philadelphia school children and was subsequently replicated in the U.S. population by Rowe and colleagues (Reference Rowe, Jacobson and van den Oord1999). Turkheimer et al. (Reference Turkheimer, Haley, Waldron, D'Onofrio and Gottesman2003) reported one of the largest Scarr–Rowe effects, finding that among those with the lowest SES, the heritability of IQ was close to zero.
A meta-analysis of 43 effect sizes sourced from 14 Scarr–Rowe effect studies found clear indications of geographic clustering (Tucker-Drob & Bates, Reference Tucker-Drob and Bates2015). A significant Scarr–Rowe effect (operationalized as a genetic additivity × SES interaction) was present among the U.S. population (ρ = 0.07, SE = 0.03, p = .003); but among populations sampled from Western Europe and Australia, the effect was absent (ρ = −0.03, SE = 0.02, p = .223). Even removing the U.S. effect sizes reported by Turkheimer's group (which were among the largest observed) yielded a significant Scarr–Rowe effect for this country (ρ = 0.06, SE = 0.02, p = .003), and also significant differences between the U.S. and non-U.S. samples (Δρ = 0.09, SE = 0.03, p = .005). This meta-analysis also yielded indications of rising heritability with age (the Wilson effect), but no evidence that the Scarr–Rowe effects were smaller among samples in which IQ had been measured at a later age. A recently published large N (1,636,968) genetically informed study of the population of Florida, containing 24,640 twins and 274,786 siblings, found no evidence for the Scarr–Rowe effect, even though the sample used was highly socioeconomically heterogeneous (Figlio et al., Reference Figlio, Freese, Karbownik and Roth2017). It should be noted, however, that this study was conducted without knowledge of zygosity, which potentially offsets some of the increment in statistical power.
The recent availability of high-quality polygenic scores (PGS; normally distributed genetic indices constructed by summing alleles from a genome wide association study, or GWAS, on a trait of interest and multiplying them by their model β values) for educational attainment and also IQ enables a new method for estimating G×E interaction effects, as their expressivity with respect to these phenotypes (i.e., the degree to which the genotype directly influences the phenotype) can be estimated, yielding more direct indications of such interactions that overcome certain limitations inherent in the twin design (such as ambiguities regarding the causation of phenotypic convergence and divergence; see, e.g., Segal, Reference Segal2013). So far, one study has already employed genomic data in investigating the Scarr–Rowe effect on IQ (Tahmasbi et al., Reference Tahmasbi, Evans, Turkheimer and Keller2017). In this study, genome-based restricted maximum likelihood estimates of heritability (GCTA-GREML) were employed to examine the presence of Scarr–Rowe effects in a sample of 40,172 individuals —sourced from the UK BioBank database. It was found that genetic variance in IQ increased as SES decreased, yielding an anti-Scarr–Rowe effect, which, as the authors note, is consistent with the null and negative effects typically reported outside of the United States (Tucker-Drob & Bates, Reference Tucker-Drob and Bates2015).
In the present study, a large and socioeconomically representative genotyped sample of the state of Wisconsin (the Wisconsin Longitudinal Study; WLS) will be used to investigate the presence of Scarr–Rowe effects via the application of a novel (and very straightforward) method that permits the direct operationalization of the expressivity of PGS on IQ, which will be used to determine the presence of G × E interactions as a function of parental SES.
Methods
Sample and Measures
All data were collected from the WLS, a longitudinal study of a randomly selected sample of Wisconsin High School students, and their siblings, born between 1937 and 1940, which began data collection in 1957 (when the participants were in their late teens and early 20s); the most recently collected data wave is from 2011. The sample is nearly exclusively of European descent, consistent with its high representativeness of mid-century Wisconsin demographics (Herd et al., Reference Herd, Carr and Roan2014).
Polygenic Score for General Intelligence
In the period 2007–2008 and again in 2010, a large genetic data collection exercise was undertaken in which saliva samples were obtained from a total of 9,012 individuals, who were subsequently genotyped using the Illumina HumanOmniExpress array as part of a very large GWAS, examining variants predictive of individual differences in educational attainment and related cognitive phenotypes (Lee et al., Reference Lee, Wedow, Okbay, Kong, Maghzian, Zacher and Cesarini2018). For full information on genotyping procedures, see https://www.ssc.wisc.edu/wlsresearch/documentation/GWAS/Herd_QC_report.pdf. Several alternative PGS were released, each representing different collections of phenotypes against which variants had been regressed, and also different methods (e.g., GWAS vs. MTAG—a multivariate regression-based estimation method). One PGS was selected for the present analysis, PGS_EA3_MTAG (henceforth EA3), which was trained via multivariate analysis with respect to several convergent cognitive phenotypes, including an IQ test from UK BioBank, various neuropsychological functioning tests and IQ subscales from COGENT, self-reported mathematical ability, and highest mathematics class successfully completed. Finally, also included among the training phenotypes was educational attainment, defined based on the 1997 ISCED UNEASCO classification, which ranks individuals based on seven internationally comparable categories of educational attainment, rescaled in terms of U.S. equivalent years of schooling. EA3 comes closest to capturing variance with respect to an overarching general intelligence factor. It should finally be noted that the sample from which Lee et al. (Reference Lee, Wedow, Okbay, Kong, Maghzian, Zacher and Cesarini2018) derived EA3 was extremely large (N > 1 million; WLS was but a small part of the overall sample) and was ethnically heterogeneous, thus EA3 is corrected for population stratification. This, coupled with the extremely high ethnic homogeneity of the WLS sample (Herd et al., Reference Herd, Carr and Roan2014), eliminates the need to include additional controls for population stratification in analyses utilizing these scores.
An additional step was taken to reduce model autocorrelation by only selecting one sibling from each family. Based on WLS recommendations, we employed the following selection protocol. When there is at least one graduate with EA3, we select the first graduate listed. In the event that there are no graduates with EA3, but there is at least one sibling with EA3, we selected the first listed sibling.
Henmon–Nelson Test of Mental Ability
The WLS contains participant scores on the Henmon–Nelson IQ test, which measures the domains of spatial, verbal, and mathematical ability. The test is timed, taking 30 min to complete, and consists of 90 items presented in ascending order of difficulty. The test was standardized state-wide in Wisconsin during the initial 1957 data collection wave, when the participants were in their late teens and early 20s. The test exhibits excellent psychometric characteristics, including high internal consistency (α ≈ 0.95; Hansen, Reference Hansen1968; Harley, Reference Harley1977) and also high convergent validity with respect to other measures of IQ, correlating in the r ≈ 0.80–0.85 range with Fullscale IQ as measured using the WAIS (Klett et al., Reference Klett, Watson and Hoffman1986; Kling et al., Reference Kling, Davis and Knost1978). The same test was administered to the participant's siblings (N = 852) in a subsequent survey wave (1977), when the participants were in their late 30s and early 40s. To compute a combined IQ measure for the entire cohort, we standardized each cohort's IQ scores separately and then merged them together (thus controlling for any divergent factors that may have influenced the IQs of each group, such as age at test administration). The resultant merged score was then restandardized.
Parental SES
The WLS contains a factor-weighted composite measure of parental SES. This measure is comprised of father's years of schooling, mother's years of schooling, Duncan's socioeconomic index for father's 1957 occupation, and average parental income, with estimates for missing data. All data were collected in the 1957 wave.
Sex
Data on the sex of WLS respondents were collected in order to test for sex differences in the magnitudes of any Scarr–Rowe effects that might be present. This variable was measured in 1957, with 1 = male and 2 = female.
Analytical Strategy
For the present analysis, the Continuous parameter estimation model (CPEM) will be used to test for Scarr–Rowe effects on genetic expressivity. CPEM was developed by Gorsuch (Reference Gorsuch2005) and is based on the mathematics of the Pearson product moment correlation. The formula for the Pearson correlation can be written as r = Σ(zx∗zy)/N, where zx and zy are the standardized scores for the independent and dependent variables, respectively, and zx∗zy is the dot product term for the two—the average of which across subjects yields the correlation coefficient r. Gorsuch (Reference Gorsuch2005) proposed that the product term (zx∗zy) for each individual is mathematically equivalent to a correlation for an N of 1. That a dot product for a single pair of observations from a single individual can function equivalently to a correlation is logically entailed by the fact that it encapsulates two properties, sign, and magnitude. When two equivalently signed z-score values are combined, the resultant product term will always be positive, indicating that the vector of deviation from the mean is conserved for both of the observations. Thus, two negatively and two positively signed observations will always yield a positively signed product term—equivalent to two negatively or positively covarying parameters in conventional correlational analysis. Opposingly, signed observations (i.e., where one is positively and the other negatively deviated with respect to the means) will always yield negative product terms—as with negatively covarying parameters in correlational analysis. The second property is magnitude, which relates to the dispersion, or absolute difference between the observations comprising the product terms. Thus, the dot product term functions as a continuous parameter estimate (CPE) of the covariance between the independent and dependent variables for each individual in the sample and can be used in regression models along with other variables for moderation analysis.
A very fruitful application of this technique has been for examining differentiation effects, such as the cognitive and strategic (behavioral) differentiation–integration effort effects, where covariance among clusters of cognitive abilities or behavioral indicators is expected to vary as a function of participants’ life history speed (Figueredo et al., Reference Figueredo, Woodley, Brown and Ross2013; Woodley et al., Reference Woodley, Figueredo, Ross and Brown2013). CPEM has also been utilized in the estimation of individual-level heritabilities derived using the correlational Falconer's formula, for the purpose of examining whether the heritability of the latent life history K factor decreases as level of K increases (Woodley of Menie et al., Reference Woodley of Menie, Figueredo, Cabeza de Baca, Fernandes, Madison, Wolf and Black2015). The technique has been used as an alternative to the method of correlated vectors in establishing latent variable moderation effects (Woodley of Menie et al., Reference Woodley of Menie, Figueredo, Cabeza de Baca, Fernandes, Madison, Wolf and Black2015), in quantifying the impact of age on assortative mating on emotional intelligence (Śmieja & Stolarski, Reference Śmeieja and Stolarski2018), in examining the role of SES as a moderator of the association between stable life history strategy and sexual debut (Dunkel et al., Reference Dunkel, Summerville, Mathes and Kesserling2015), and for examining the curvilinear associations between longitudinal trends among the WAIS scale-scores and participant age (Lee et al., Reference Lee, Gorsuch, Saklofske and Patterson2008), among other things.
Here, it is proposed that CPEM can be used to compute the individual-level covariance among EA3 and IQ scores for each participant utilizing the dot product terms to capture the strength of the association between subject genotype and phenotype, which is a direct measure of genetic expressivity. By regressing parental SES against the CPE, the presence of a Scarr–Rowe effect can be determined if the resulting β value is positive, as this would indicate that the genetic expressivity (i.e., the covariance) of EA3 to IQ increases as parental SES increases. Given that large amounts of data are available in WLS for both sexes, comparison of the effect sizes can be used to determine the presence of a sex difference in the effect. All analyses were conducted in R and the code is publicly archived at http://rpubs.com/Jonatan/cpem
Results
Analysis 1: Combined Sample
Table 1 presents the descriptive statistics and correlations for the variables utilized in the analysis of the combined sample.
TABLE 1 Descriptive Statistics and Correlations for the Combined Sex Sample

All correlations are significant at <0.001.
More information on the descriptives is available at http://rpubs.com/Jonatan/cpem. Table 2 presents the results of the CPEM analysis. As is standard in analyses involving CPEM, all variables are standardized prior to entry into the regression (e.g., Figueredo et al., Reference Figueredo, Woodley, Brown and Ross2013). This means that the resultant b values correspond to standardized β values, and no intercept term needs to be computed, yielding one additional model degree of freedom (the results including the intercepts are available at the Rpubs archive). In addition to the CPEM regression parameter, the model residual skewness is also estimated in order to ensure that there are no normality violations.
TABLE 2 The Results of Regressing the CPE z(EA3)*z(IQ), Which Captures Differences in Levels of Genetic Expressivity on Parental SES
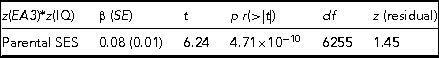
The model t statistic, significance, degrees of freedom and the skew on the model residual are also presented. Adj. R 2 = 0.006, F = 38.92.
The regression model yields indications of a small-magnitude (i.e., <0.29; Cohen, Reference Cohen1988) Scarr–Rowe effect when parental SES is used to predict variation in the genetic expressivity of the participants’ PGS on their IQ scores. The effect is highly statistically significant (which is unremarkable given the very high model degrees of freedom) and the skew on the model residual falls within the levels generally considered acceptable for parametric regression (i.e., z between +2 and -2; George & Mallery, Reference George and Mallery2010). The results of this analysis are graphed in Figure 1.
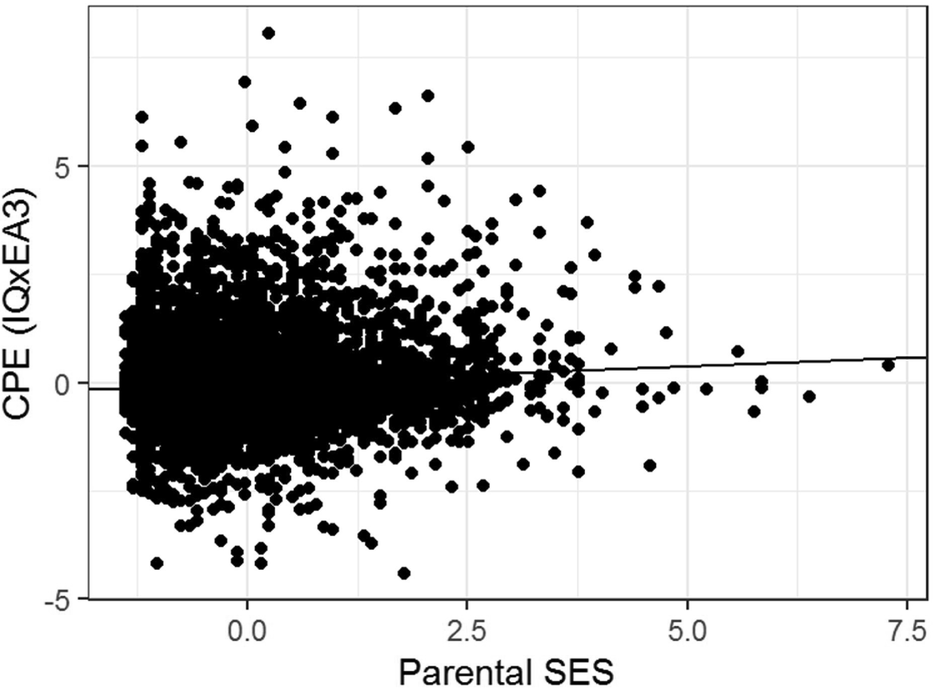
FIGURE 1 Scatter plot and regression line of the CPE z(EA3)*z(IQ) capturing individual differences in genetic expressivity as a function of parental SES for the combined sample, N = 6,256.
Analysis 2: Broken Out by Sex
Table 3 presents the correlations broken out by sex.
TABLE 3 Correlations Broken Out by Sex, with Males below the Diagonal and Females Above
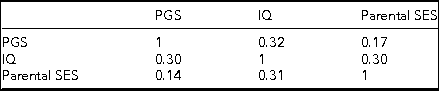
All correlations are significant at p < .001.
Table 4 presents the results of CPEM analyses for males and females separately. In addition to the CPEM regression parameter, the model residual skewness is also estimated for both regressions in order to ensure that there are no normality violations.
TABLE 4 The Results of Regressing the CPE z(EA3)*z(IQ), Which Captures Differences in Levels of Genetic Expressivity Against Parental SES for Males (Top Row) and Females (Bottom Row) Separately

The model t statistics, significances, degrees of freedom, and the skew on the model residuals are also presented. Males adj. R 2 = 0.005, F = 16.4. Females adj. R 2 = 0.007, F = 22.75.
The effect is present in both males and females separately and to an equal extent, indicating no sex differences. As with the combined sample, the residual model skewness falls within the acceptable range of values (i.e., z between +2 and -2).
Robustness Analysis 1: Outlier Removal
To test the robustness of the effects to potentially outlying values of parental SES, the analyses were rerun for the combined sample and male and female subsamples, excluding all values of parental SES that were >+3 standard deviations above the mean (the 3 SD labeling method; Seo, Reference Seo2002). The results of this analysis are presented in Table 5. The results indicate that outlying values of parental SES are not driving these effects and that there is only a very small reduction in the effect sizes for the combined sample and the male and female subsamples.
TABLE 5 The Results of Regressing the CPE z(EA3)*z(IQ), Which Captures Differences in Levels of Genetic Expressivity Against Parental SES for the Combined Sample (Top Row), Males (Middle Row) and Females (Bottom Row) Separately. Outlying values of parental SES ≥+3 SD removed.

The model t statistics, significances, degrees of freedom, and the skew on the model residuals are also presented. Combined sample adj. R 2 = 0.004, F = 24.99, Males adj. R 2 = 0.002, F = 7.25. Females adj. R 2 = 0.006, F = 19.09.
Robustness Analysis 2: Log-Transformation of Parental SES
Of all of the variables utilized, the most heavily skewed was parental SES (z = 1.29). Although regression analysis does not require that the inputs be normally distributed, relatively pronounced deviation from normality can nevertheless cause skew in the model residual, which may affect the stability of the result when this is pronounced. Table 6 presents the results of utilizing (natural) log-transformed parental SES as the predictor. Doing so very slightly reduces the effect sizes for the combined sample and male and female subsamples.
TABLE 6 The Results of Regressing the CPE z(EA3)*z(IQ), Which Captures Differences in Levels of Genetic Expressivity Against Log-Transformed Parental SES for Males (Top Row) and Females (Bottom Row) Separately

The model t statistics, significances, degrees of freedom, and the skew on the model residuals are also presented. Combined sample adj. R 2 = 0.002, F = 15.92, Males adj. R 2 = 0.002, F = 7.84. Females adj. R 2 = 0.002, F = 8.08.
Robustness Analysis 3: Comparison with a Conventional Two-Way Interaction Model
The conventional method for estimating Scarr–Rowe effects is via a two-way interaction term between the genetic parameter and SES, estimated net of the main effects of the two (or in the case of behavior genetic studies, four) constituent variables (i.e., A, C, E, and SES), with IQ as the dependent variable (Tucker-Drobb & Bates, Reference Tucker-Drob and Bates2015). Based on a simulation (which can be viewed at http://jsmp.dk/files/cpem_sim.html), we expect the results of CPEM and a two-way interaction model to be similar, with the former enjoying a slight advantage in terms of model degrees of freedom. Consistent with this, the interaction model (presented in Table 7; note that as all terms were standardized prior to entry into the regression no intercept was estimated) yields a similar β value to the CPEM analysis when log-transformed SES is used in both cases. The reduced model degrees of freedom in the interaction model (6,253 vs. 6,255), coupled with the slightly lower magnitude effect size (β = 0.02 vs. 0.05), led to a non-significant value for the EA3 × parental SES interaction term. Despite this, given that the results of the CPEM analysis and the prior meta-analysis of U.S. studies based on the use of twins and siblings permit a directional prediction of the interaction effect to be made, the use of one-tailed significance is justified in this instance (Kimmel, Reference Kimmel1957), which yields a significant result (p = .045).
TABLE 7 The Results of a Regression Model Using IQ to Predict EA3, Log Parental SES and the Two-Way Interaction Between EA3 and Log Parental SES

The model t statistics and significances are also presented. adj. R2 = 0.16, F = 390 on 3 and df = 6253, p < 2.2×10−16.
Discussion
An analysis using CPEM indicates the presence of an apparent Scarr–Rowe effect on the genetic expressivity of EA3 capturing variance in general intelligence on a phenotypic measure of intelligence in a large study. Genetic expressivity increases as SES increases, consistent with the findings of gene × SES interaction effects from U.S. cohorts (Tucker-Drob & Bates, Reference Tucker-Drob and Bates2015), which means that the present method of estimating the effect using the differential expressivity of EA3 on IQ as a function of SES yields equivalent results to studies estimating gene × SES interaction effects derived using more conventional behavior genetic approaches (i.e., biometric structural equation modeling involving twins and siblings). This is illustrated via both simulation and comparison of CPEM results to a regression analysis involving a two-way interaction between EA3 and log-transformed parental SES, which yielded a (one-tailed significant) interaction effect. Furthermore, to the best of our knowledge, this is the first time that the possibility of sex differences in the Scarr–Rowe effect has been investigated, with no apparent difference in the magnitudes being present.
While these findings are supportive of the existence of the Scarr–Rowe effect and are broadly congruent with relevant studies from the United States, there is evidence that not all parts of the United States are equally conducive to the effect, possibly due to high SES variation both within and among U.S. States. The Florida cohort study of Figlio et al. (Reference Figlio, Freese, Karbownik and Roth2017) is illustrative on this score, as it was extremely highly powered to detect the effect yet found no indications of an SES × IQ heritability interaction using both twins and siblings (although the lack of data on zygosity noted in the introduction should be kept in mind). The most conservative interpretation of our results, therefore, is that the bioecological factors that suppress the expressivity of cognitive genetic variants among those with low levels of childhood SES were present specifically among those born in the state of Wisconsin in the late 1930s and early 1940s. From this arises the question of whether there might be a secular trend in the strength of the Scarr–Rowe effect. Perhaps one reason that Figlio et al. (Reference Figlio, Freese, Karbownik and Roth2017) were unable to detect the effect in their young sample is that environmental quality in the United States among those with low SES has improved in the decades since the WLS cohort was born (the Figlio et al., Reference Figlio, Freese, Karbownik and Roth2017 cohorts were born between 1994 and 2002, approximately six decades later), thus erasing the effect. A cross-temporal, meta-analysis of the U.S. data in Tucker-Drob and Bates (Reference Tucker-Drob and Bates2015) along with the results of newer studies such as Figlio et al. (Reference Figlio, Freese, Karbownik and Roth2017) might help to determine whether such a trend exists, net of factors such as participant age at cognitive evaluation and location within the United States.
Finally, given that g has a potentially very flat norm of reaction (meaning that the trait seems to be well canalized against environmental influences experienced during childhood; Protzko, Reference Protzko2015; Sesardic, Reference Sesardic2005), it is predicted that the biggest and, critically, most persistent impact of bioecological elicitors of the Scarr–Rowe effect will be on measures of IQ exhibiting low g saturation, and thus low heritability (see, e.g., Voronin et al., Reference Voronin, te Nijenhuis and Malykh2016, Table 3, p. 835), which potentially leaves greater ‘room’ for G×E interactions in the determination of trait variance. If it is found that g loading negatively moderates ability measures’ sensitivity to the Scarr–Rowe effect, then the g loading of tests might be an important factor to control for in future meta-analyses. Moreover, it suggests that the Scarr–Rowe effect may help increase our understanding of the Flynn effect (which also occurs to the greatest extent on the least g-loaded abilities; te Nijenhuis & van der Flier, Reference te Nijenhuis and van der Flier2013), as reductions in the strength of the former effect may be a driver of the latter effect. This is because reduced variance in the provisioning of environmental factors such as educational attainment and other inducements toward cognitive specialization may be boosting opportunities for those with low SES to reach their genetic potential in terms of their capacity to cultivate specialized abilities, leading to potentially large gains in IQ, especially in instances where the transition from a poor- to a high-quality environment is very rapid. This may explain why in a substantial subset of studies, the Flynn effect appears to be larger among those with lower levels of IQ (which tracks lower SES; e.g., Flynn, Reference Flynn2012).










