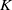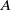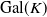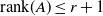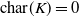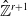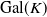1. Introduction
A consequence of class field theory appearing in [Reference Ribes9, p. 302, Thm. 8.8(b)(iii)] says that the cohomological dimension of every number field
![]() $K$
which is not embeddable in
$K$
which is not embeddable in
![]() $\mathbb{R}$
is
$\mathbb{R}$
is
![]() $2$
. On the other hand,
$2$
. On the other hand,
![]() $\mathrm{cd}({\hat{\mathbb{Z}}}\times{\hat{\mathbb{Z}}})=2$
[Reference Ribes9, p. 217, Cor. 3.2 and p. 221, Prop. 4.4] and the group
$\mathrm{cd}({\hat{\mathbb{Z}}}\times{\hat{\mathbb{Z}}})=2$
[Reference Ribes9, p. 217, Cor. 3.2 and p. 221, Prop. 4.4] and the group
![]() $\hat{\mathbb{Z}}$
occurs as a closed subgroup of
$\hat{\mathbb{Z}}$
occurs as a closed subgroup of
![]() $\textrm{Gal}(\mathbb{Q})$
in many ways [Reference Fried and Jarden3, p. 379, Thm. 18.5.6]. One may therefore wonder whether
$\textrm{Gal}(\mathbb{Q})$
in many ways [Reference Fried and Jarden3, p. 379, Thm. 18.5.6]. One may therefore wonder whether
![]() ${\hat{\mathbb{Z}}}\times{\hat{\mathbb{Z}}}$
is isomorphic to a closed subgroup of
${\hat{\mathbb{Z}}}\times{\hat{\mathbb{Z}}}$
is isomorphic to a closed subgroup of
![]() $\textrm{Gal}(\mathbb{Q})$
.
$\textrm{Gal}(\mathbb{Q})$
.
A somewhat surprising result of Geyer’s thesis says that this is not the case. Indeed, every closed abelian subgroup of
![]() $\textrm{Gal}(\mathbb{Q})$
is procyclic [Reference Geyer4, p. 357, Satz 2.3] (see also [Reference Ribes9, p. 306, Thm. 9.1]).
$\textrm{Gal}(\mathbb{Q})$
is procyclic [Reference Geyer4, p. 357, Satz 2.3] (see also [Reference Ribes9, p. 306, Thm. 9.1]).
We generalize this result for every finitely generated extension
![]() $K$
of transcendence degree
$K$
of transcendence degree
![]() $r$
of a global field. We prove that if a profinite group
$r$
of a global field. We prove that if a profinite group
![]() $A$
is isomorphic to a closed abelian subgroup of
$A$
is isomorphic to a closed abelian subgroup of
![]() $\textrm{Gal}(K)$
, then
$\textrm{Gal}(K)$
, then
![]() ${\mathrm{rank}}(A)\le r+1$
. In particular,
${\mathrm{rank}}(A)\le r+1$
. In particular,
![]() ${\hat{\mathbb{Z}}}^{r+2}$
is not a subgroup of
${\hat{\mathbb{Z}}}^{r+2}$
is not a subgroup of
![]() $\textrm{Gal}(K)$
(Proposition 4.3).
$\textrm{Gal}(K)$
(Proposition 4.3).
In the rest of this note, we abuse our language and write “
![]() $A$
is a closed subgroup of
$A$
is a closed subgroup of
![]() $\textrm{Gal}(K)$
” rather than “
$\textrm{Gal}(K)$
” rather than “
![]() $A$
is isomorphic to a closed subgroup of
$A$
is isomorphic to a closed subgroup of
![]() $\textrm{Gal}(K)$
.”
$\textrm{Gal}(K)$
.”
It turns out that the latter inequality is sharp. Indeed, if
![]() $\mathrm{char}(K)=0$
, then
$\mathrm{char}(K)=0$
, then
![]() ${\hat{\mathbb{Z}}}^{r+1}$
is a closed subgroup of
${\hat{\mathbb{Z}}}^{r+1}$
is a closed subgroup of
![]() $\textrm{Gal}(K)$
, while if
$\textrm{Gal}(K)$
, while if
![]() $\mathrm{char}(K)=p\gt 0$
, then
$\mathrm{char}(K)=p\gt 0$
, then
![]() $\hat{\mathbb{Z}}$
is a closed subgroup of
$\hat{\mathbb{Z}}$
is a closed subgroup of
![]() $\textrm{Gal}(K)$
,
$\textrm{Gal}(K)$
,
![]() $\prod _{l\ne p}\mathbb{Z}_l^{r+1}$
is a closed subgroup of
$\prod _{l\ne p}\mathbb{Z}_l^{r+1}$
is a closed subgroup of
![]() $\textrm{Gal}(K)$
if
$\textrm{Gal}(K)$
if
![]() $r\ge 0$
(Theorem 5.7), but
$r\ge 0$
(Theorem 5.7), but
![]() ${\hat{\mathbb{Z}}}^{r+1}$
is not a closed subgroup of
${\hat{\mathbb{Z}}}^{r+1}$
is not a closed subgroup of
![]() $\textrm{Gal}(K)$
if
$\textrm{Gal}(K)$
if
![]() $r\ge 1$
(Remark 5.8). Here
$r\ge 1$
(Remark 5.8). Here
![]() $l$
ranges over the prime numbers. The exclusion of the factor
$l$
ranges over the prime numbers. The exclusion of the factor
![]() $\mathbb{Z}_p$
in the case when
$\mathbb{Z}_p$
in the case when
![]() $p\gt 0$
and
$p\gt 0$
and
![]() $r\ge 1$
follows from the rule
$r\ge 1$
follows from the rule
![]() $\mathrm{cd}_p(\textrm{Gal}(F))\le 1$
for each field
$\mathrm{cd}_p(\textrm{Gal}(F))\le 1$
for each field
![]() $F$
of characteristic
$F$
of characteristic
![]() $p$
[Reference Ribes9, p. 256, Thm. 3.3].
$p$
[Reference Ribes9, p. 256, Thm. 3.3].
2. Preliminaries
One of the basic tools needed in the proof of the generalization of Geyer’s result is a special case of the renowned Pontryagin–van Kampen theorem. Here, and in the rest of this note,
![]() $l$
stands for a prime number,
$l$
stands for a prime number,
![]() $\mathbb{Z}_l$
is the ring of
$\mathbb{Z}_l$
is the ring of
![]() $l$
-adic numbers, viewed as a profinite abelian group or as a principal ideal domain. We also write
$l$
-adic numbers, viewed as a profinite abelian group or as a principal ideal domain. We also write
![]() ${\hat{\mathbb{Z}}}\;:\!=\;\prod _l\mathbb{Z}_l$
for the Prüfer group [Reference Fried and Jarden3, p. 12]. Thus,
${\hat{\mathbb{Z}}}\;:\!=\;\prod _l\mathbb{Z}_l$
for the Prüfer group [Reference Fried and Jarden3, p. 12]. Thus,
![]() $\mathbb{Z}_l$
is the free pro-
$\mathbb{Z}_l$
is the free pro-
![]() $l$
cyclic group and
$l$
cyclic group and
![]() $\hat{\mathbb{Z}}$
is the free procyclic group.
$\hat{\mathbb{Z}}$
is the free procyclic group.
Proposition 2.1 ([Reference Ribes and Zalesskii10, p. 129, Thm. 4.3.3]). Let
![]() $A$
be a torsion-free abelian profinite group. Then
$A$
be a torsion-free abelian profinite group. Then
![]() $A\cong \prod _l\mathbb{Z}_l^{r_l}$
, where
$A\cong \prod _l\mathbb{Z}_l^{r_l}$
, where
![]() $r_l$
is a cardinal number for each
$r_l$
is a cardinal number for each
![]() $l$
.
$l$
.
The proof of Proposition 2.1 uses a special case of the Pontryagin–van Kampen duality theorem saying that every locally compact abelian topological group
![]() $A$
is canonically isomorphic to its double dual group
$A$
is canonically isomorphic to its double dual group
![]() $A^{**}$
, where
$A^{**}$
, where
![]() $A^*={\mathrm{Hom}}(A,\mathbb{R}/\mathbb{Z})$
. The proof of that special case needed in our proposition, dealing only with abelian profinite groups, appears in [Reference Ribes and Zalesskii10, Section 2.9]. It is much simpler than the proof of the general theorem [Reference Hewitt and Ross5, p. 376, Thm. 24.2].
$A^*={\mathrm{Hom}}(A,\mathbb{R}/\mathbb{Z})$
. The proof of that special case needed in our proposition, dealing only with abelian profinite groups, appears in [Reference Ribes and Zalesskii10, Section 2.9]. It is much simpler than the proof of the general theorem [Reference Hewitt and Ross5, p. 376, Thm. 24.2].
We denote the algebraic closure of a field
![]() $K$
by
$K$
by
![]() $\tilde{K}$
and its separable algebraic closure by
$\tilde{K}$
and its separable algebraic closure by
![]() $K_{\mathrm{sep}}$
. We write
$K_{\mathrm{sep}}$
. We write
![]() $\textrm{Gal}(K)$
for the absolute Galois group
$\textrm{Gal}(K)$
for the absolute Galois group
![]() $\textrm{Gal}(K_{\mathrm{sep}}/K)$
of
$\textrm{Gal}(K_{\mathrm{sep}}/K)$
of
![]() $K$
. If
$K$
. If
![]() $A$
is a closed subgroup of
$A$
is a closed subgroup of
![]() $\textrm{Gal}(K)$
, then
$\textrm{Gal}(K)$
, then
![]() $K_{\mathrm{sep}}(A)$
denotes the fixed field of
$K_{\mathrm{sep}}(A)$
denotes the fixed field of
![]() $A$
in
$A$
in
![]() $K_{\mathrm{sep}}$
.
$K_{\mathrm{sep}}$
.
Lemma 2.2.
Let
![]() $K$
be a field and
$K$
be a field and
![]() $A$
a nontrivial finite subgroup of
$A$
a nontrivial finite subgroup of
![]() $\textrm{Gal}(K)$
. Then,
$\textrm{Gal}(K)$
. Then,
![]() $A\cong \mathbb{Z}/2\mathbb{Z}$
,
$A\cong \mathbb{Z}/2\mathbb{Z}$
,
![]() $\mathrm{char}(K)=0$
, and the fixed field
$\mathrm{char}(K)=0$
, and the fixed field
![]() ${\tilde{K}}(A)$
of
${\tilde{K}}(A)$
of
![]() $A$
in
$A$
in
![]() $\tilde{K}$
is real closed. In addition,
$\tilde{K}$
is real closed. In addition,
![]() $A$
is the centralizer of itself in
$A$
is the centralizer of itself in
![]() $\textrm{Gal}(K)$
.
$\textrm{Gal}(K)$
.
Proof. Let
![]() $R=K_{\mathrm{sep}}(A)$
. Then, a theorem of Artin says that
$R=K_{\mathrm{sep}}(A)$
. Then, a theorem of Artin says that
![]() $\mathrm{char}(K)=0$
,
$\mathrm{char}(K)=0$
,
![]() $K_{\mathrm{sep}}={\tilde{K}}$
, and
$K_{\mathrm{sep}}={\tilde{K}}$
, and
![]() ${\tilde{K}}=R(\sqrt{-1})$
[Reference Lang7, p. 299, Cor. 9.3]. Let
${\tilde{K}}=R(\sqrt{-1})$
[Reference Lang7, p. 299, Cor. 9.3]. Let
![]() $\tau$
be the unique element of order
$\tau$
be the unique element of order
![]() $2$
of
$2$
of
![]() $\textrm{Gal}(R)$
defined by
$\textrm{Gal}(R)$
defined by
![]() $\tau (\sqrt{-1})=-\sqrt{-1}$
.
$\tau (\sqrt{-1})=-\sqrt{-1}$
.
By [Reference Lang7, p. 452, Prop. 2.4],
![]() $R$
is real closed. Let
$R$
is real closed. Let
![]() $\lt$
be the ordering of
$\lt$
be the ordering of
![]() $K$
induced by the unique ordering of
$K$
induced by the unique ordering of
![]() $R$
. If
$R$
. If
![]() $R'$
is a real closed field extension of
$R'$
is a real closed field extension of
![]() $K$
in
$K$
in
![]() $\tilde{K}$
whose ordering extends
$\tilde{K}$
whose ordering extends
![]() $\lt$
, then by [Reference Lang7, p. 455, Thm. 2.9], there exists a unique
$\lt$
, then by [Reference Lang7, p. 455, Thm. 2.9], there exists a unique
![]() $K$
-isomorphism
$K$
-isomorphism
![]() $R\to R'$
.
$R\to R'$
.
Let
![]() $\sigma$
be an element of the centralizer
$\sigma$
be an element of the centralizer
![]() $C_{\textrm{Gal}(K)}(A)$
of
$C_{\textrm{Gal}(K)}(A)$
of
![]() $A$
in
$A$
in
![]() $\textrm{Gal}(K)$
. Then,
$\textrm{Gal}(K)$
. Then,
![]() $\sigma R$
is a real closure of
$\sigma R$
is a real closure of
![]() $(K,\lt )$
and
$(K,\lt )$
and
![]() $\textrm{Gal}(\sigma R)\cong \mathbb{Z}/2\mathbb{Z}$
. Also,
$\textrm{Gal}(\sigma R)\cong \mathbb{Z}/2\mathbb{Z}$
. Also,
![]() $\tau (\sigma R)=\tau \sigma R=\sigma \tau R=\sigma R$
. By the preceding paragraph applied to
$\tau (\sigma R)=\tau \sigma R=\sigma \tau R=\sigma R$
. By the preceding paragraph applied to
![]() $\sigma R$
rather than to
$\sigma R$
rather than to
![]() $R$
, the restriction of
$R$
, the restriction of
![]() $\tau$
to
$\tau$
to
![]() $\sigma R$
is the identity map. In other words,
$\sigma R$
is the identity map. In other words,
![]() $\tau \in \textrm{Gal}(\sigma R)$
. Since
$\tau \in \textrm{Gal}(\sigma R)$
. Since
![]() ${\mathrm{ord}}(\tau )=2$
, the element
${\mathrm{ord}}(\tau )=2$
, the element
![]() $\tau$
generates
$\tau$
generates
![]() $\textrm{Gal}(\sigma R)$
, so
$\textrm{Gal}(\sigma R)$
, so
![]() $R=\sigma R$
. The uniqueness of the
$R=\sigma R$
. The uniqueness of the
![]() $K$
-isomorphism of
$K$
-isomorphism of
![]() $R$
into
$R$
into
![]() $R$
implies that
$R$
implies that
![]() $\sigma \in \textrm{Gal}(R)=A$
, as desired.
$\sigma \in \textrm{Gal}(R)=A$
, as desired.
Corollary 2.3.
Let
![]() $K$
be a field and
$K$
be a field and
![]() $A$
a closed abelian subgroup of
$A$
a closed abelian subgroup of
![]() $\textrm{Gal}(K)$
. Then,
$\textrm{Gal}(K)$
. Then,
![]() $A\cong \mathbb{Z}/2\mathbb{Z}$
or
$A\cong \mathbb{Z}/2\mathbb{Z}$
or
![]() $A\cong \prod _l\mathbb{Z}_l^{r_l}$
, where
$A\cong \prod _l\mathbb{Z}_l^{r_l}$
, where
![]() $l$
ranges over all prime numbers and
$l$
ranges over all prime numbers and
![]() $r_l$
is a cardinal number.
$r_l$
is a cardinal number.
Proof. If
![]() $A$
has a non-unit element
$A$
has a non-unit element
![]() $\alpha$
of a finite order, then by Lemma 2.2,
$\alpha$
of a finite order, then by Lemma 2.2,
![]() $\langle \alpha \rangle \cong \mathbb{Z}/2\mathbb{Z}$
and
$\langle \alpha \rangle \cong \mathbb{Z}/2\mathbb{Z}$
and
![]() $\langle \alpha \rangle$
is its own centralizer in
$\langle \alpha \rangle$
is its own centralizer in
![]() $\textrm{Gal}(K)$
. Since
$\textrm{Gal}(K)$
. Since
![]() $A$
is abelian,
$A$
is abelian,
![]() $A$
is contained in that centralizer. Therefore,
$A$
is contained in that centralizer. Therefore,
![]() $A=\langle \alpha \rangle$
.
$A=\langle \alpha \rangle$
.
Otherwise,
![]() $A$
is torsion-free. Hence, by Proposition 2.1,
$A$
is torsion-free. Hence, by Proposition 2.1,
![]() $A$
has the desired structure.
$A$
has the desired structure.
Given a profinite group
![]() $G$
and a prime number
$G$
and a prime number
![]() $l$
, we write
$l$
, we write
![]() $\mathrm{cd}_l(G)$
for the
$\mathrm{cd}_l(G)$
for the
![]() $\textit{l}$
th cohomology dimension of
$\textit{l}$
th cohomology dimension of
![]() $\textbf{G}$
[Reference Ribes9, p. 196, Def. 1.1]. Also, we write
$\textbf{G}$
[Reference Ribes9, p. 196, Def. 1.1]. Also, we write
![]() $\zeta _n$
for a primitive root of unity of order
$\zeta _n$
for a primitive root of unity of order
![]() $n$
.
$n$
.
Lemma 2.4.
The following statements hold for prime numbers
![]() $p,l$
, and a finite extension
$p,l$
, and a finite extension
![]() $E$
of
$E$
of
![]() $\mathbb{Q}_p$
:
$\mathbb{Q}_p$
:
-
(a)
 $E$
contains only finitely many roots of unity.
$E$
contains only finitely many roots of unity.
-
(b)
 $l^\infty |[E(\zeta _{l^j})_{j\ge 1}\;:\;E]$
.
$l^\infty |[E(\zeta _{l^j})_{j\ge 1}\;:\;E]$
. -
(c)
 $\mathrm{cd}_l(\textrm{Gal}(E(\zeta _{l^j})_{j\ge 1}))\le 1$
.
$\mathrm{cd}_l(\textrm{Gal}(E(\zeta _{l^j})_{j\ge 1}))\le 1$
.
Proof of (a). Let
![]() $O$
be the ring of integers of
$O$
be the ring of integers of
![]() $E$
,
$E$
,
![]() $\bar{E}$
the residue field of
$\bar{E}$
the residue field of
![]() $E$
,
$E$
,
![]() $\pi$
a prime element of
$\pi$
a prime element of
![]() $O$
,
$O$
,
![]() $U$
the group of invertible elements of
$U$
the group of invertible elements of
![]() $O$
, and
$O$
, and
![]() $U^{(1)}=1+\pi O$
the subgroup of
$U^{(1)}=1+\pi O$
the subgroup of
![]() $1$
-units of
$1$
-units of
![]() $O$
. Reduction modulo
$O$
. Reduction modulo
![]() $\pi O$
yields the following short exact sequence
$\pi O$
yields the following short exact sequence
where
![]() $\textbf{1}$
is the trivial group. By [Reference Serre11, p. 213, Chap. XIV, Prop. 10],
$\textbf{1}$
is the trivial group. By [Reference Serre11, p. 213, Chap. XIV, Prop. 10],
![]() $U^{(1)}$
is isomorphic to a direct product of a finite abelian group with a free abelian group. Since
$U^{(1)}$
is isomorphic to a direct product of a finite abelian group with a free abelian group. Since
![]() ${\bar{E}}^\times$
is also finite, the torsion group of
${\bar{E}}^\times$
is also finite, the torsion group of
![]() $U$
is finite. That group is the group of roots of unity in
$U$
is finite. That group is the group of roots of unity in
![]() $E$
.
$E$
.
Proof of (b). By (a),
![]() $E$
has only finitely many roots of unity of order
$E$
has only finitely many roots of unity of order
![]() $l^j$
with
$l^j$
with
![]() $j\ge 1$
. Thus, there exists a non-negative integer
$j\ge 1$
. Thus, there exists a non-negative integer
![]() $j$
with
$j$
with
![]() $\zeta _{l^j}\in E$
and
$\zeta _{l^j}\in E$
and
![]() $\zeta _{l^{j+1}}\notin E$
. By [Reference Lang7, p. 297, Thm. 9.1],
$\zeta _{l^{j+1}}\notin E$
. By [Reference Lang7, p. 297, Thm. 9.1],
![]() $[E(\zeta _{l^{j+1}})\;:\;E(\zeta _{l^j})]=l$
. Apply the same argument to the field
$[E(\zeta _{l^{j+1}})\;:\;E(\zeta _{l^j})]=l$
. Apply the same argument to the field
![]() $E_1\;:\!=\;E(\zeta _{l^{j+1}})$
to find an integer
$E_1\;:\!=\;E(\zeta _{l^{j+1}})$
to find an integer
![]() $j_2\gt j_1\;:\!=\;j$
such that
$j_2\gt j_1\;:\!=\;j$
such that
![]() $\zeta _{l^{j_2}}\in E_1$
and
$\zeta _{l^{j_2}}\in E_1$
and
![]() $\zeta _{l^{j_2+1}}\notin E_1$
, so
$\zeta _{l^{j_2+1}}\notin E_1$
, so
![]() $[E_2\;:\;E_1]=l$
with
$[E_2\;:\;E_1]=l$
with
![]() $E_2\;:\!=\;E(\zeta _{l^{j_1+1}},\zeta _{l^{j_2+1}})$
. Continue to find a sequence
$E_2\;:\!=\;E(\zeta _{l^{j_1+1}},\zeta _{l^{j_2+1}})$
. Continue to find a sequence
![]() $j_1\lt j_2\lt j_3\lt \dots$
and fields
$j_1\lt j_2\lt j_3\lt \dots$
and fields
![]() $E\subset E_1\subset E_2\subset E_3\subset \cdots$
such that
$E\subset E_1\subset E_2\subset E_3\subset \cdots$
such that
![]() $\zeta _{l^{j_{n+1}}}\in E_n\;:\!=\;E(\zeta _{l^{j_i+1}})_{i=1}^n$
and
$\zeta _{l^{j_{n+1}}}\in E_n\;:\!=\;E(\zeta _{l^{j_i+1}})_{i=1}^n$
and
![]() $\zeta _{l^{j_{n+1}+1}}\notin E_n$
, so
$\zeta _{l^{j_{n+1}+1}}\notin E_n$
, so
![]() $[E_{n+1}\;:\;E_n]=l$
, for each
$[E_{n+1}\;:\;E_n]=l$
, for each
![]() $n\ge 1$
. Hence,
$n\ge 1$
. Hence,
![]() $l^\infty |[E(\zeta _{l^j})_{j\ge 1}\;:\;E]$
.
$l^\infty |[E(\zeta _{l^j})_{j\ge 1}\;:\;E]$
.
Proof of (c). The claim follows from (b) and [Reference Ribes9, p. 291, Cor. 7.4(i),(ii)].
Note that the citation in the proof of (c) relies on local class field theory.
3. Geyer’s theorem
We generalize Geyer’s theorem which asserts that every closed abelian subgroup of
![]() $\textrm{Gal}(\mathbb{Q})$
is procyclic [Reference Geyer4, p. 357, Satz 2.3].
$\textrm{Gal}(\mathbb{Q})$
is procyclic [Reference Geyer4, p. 357, Satz 2.3].
Lemma 3.1.
Let
![]() $F$
be a field of positive characteristic
$F$
be a field of positive characteristic
![]() $p$
. Then, no pro-
$p$
. Then, no pro-
![]() $p$
closed subgroup of
$p$
closed subgroup of
![]() $\textrm{Gal}(F)$
is isomorphic to
$\textrm{Gal}(F)$
is isomorphic to
![]() $\mathbb{Z}_p\times \mathbb{Z}_p$
.
$\mathbb{Z}_p\times \mathbb{Z}_p$
.
Proof. Let
![]() $G$
be a closed pro-
$G$
be a closed pro-
![]() $p$
subgroup of
$p$
subgroup of
![]() $\textrm{Gal}(F)$
. By [Reference Ribes9, p. 256, Thm. 3.3],
$\textrm{Gal}(F)$
. By [Reference Ribes9, p. 256, Thm. 3.3],
![]() $\mathrm{cd}(G)\le 1$
. On the other hand,
$\mathrm{cd}(G)\le 1$
. On the other hand,
![]() $\mathbb{Z}_p$
is a free pro-
$\mathbb{Z}_p$
is a free pro-
![]() $p$
group of rank
$p$
group of rank
![]() $1$
. Hence, by [Reference Ribes9, p. 217, Cor. 3.2],
$1$
. Hence, by [Reference Ribes9, p. 217, Cor. 3.2],
![]() $\mathrm{cd}(\mathbb{Z}_p)=1$
. It follows from [Reference Ribes9, p. 221, Prop. 4.4] that
$\mathrm{cd}(\mathbb{Z}_p)=1$
. It follows from [Reference Ribes9, p. 221, Prop. 4.4] that
![]() $\mathrm{cd}(\mathbb{Z}_p\times \mathbb{Z}_p)=\mathrm{cd}(\mathbb{Z}_p)+\mathrm{cd}(\mathbb{Z}_p)=2$
. Therefore,
$\mathrm{cd}(\mathbb{Z}_p\times \mathbb{Z}_p)=\mathrm{cd}(\mathbb{Z}_p)+\mathrm{cd}(\mathbb{Z}_p)=2$
. Therefore,
![]() $G\not \cong \mathbb{Z}_p\times \mathbb{Z}_p$
, as claimed.
$G\not \cong \mathbb{Z}_p\times \mathbb{Z}_p$
, as claimed.
Lemma 3.2.
Let
![]() $K$
be a global field,
$K$
be a global field,
![]() $l\ne \mathrm{char}(K)$
a prime number, and
$l\ne \mathrm{char}(K)$
a prime number, and
![]() $M$
a separable algebraic extension of
$M$
a separable algebraic extension of
![]() $K$
. Suppose that
$K$
. Suppose that
![]() $M$
contains all of the roots of unity of order
$M$
contains all of the roots of unity of order
![]() $l^i$
for
$l^i$
for
![]() $i=1,2,3,\ldots$
. Then,
$i=1,2,3,\ldots$
. Then,
![]() $\mathrm{cd}_l(\textrm{Gal}(M))\le 1$
. In particular,
$\mathrm{cd}_l(\textrm{Gal}(M))\le 1$
. In particular,
![]() $\textrm{Gal}(M)\not \cong \mathbb{Z}_l\times \mathbb{Z}_l$
.
$\textrm{Gal}(M)\not \cong \mathbb{Z}_l\times \mathbb{Z}_l$
.
Proof. We distinguish between two cases:
Case A:
![]() $K$
is a number field. We assume without loss that
$K$
is a number field. We assume without loss that
![]() $K=\mathbb{Q}$
. By assumption,
$K=\mathbb{Q}$
. By assumption,
![]() $\zeta _{l^2}\in M \newcommand{\hefreshD }{\mathop{\raise 1.5pt\hbox{${\smallsetminus }$}}} \newcommand{\hefreshS }{\mathop{\raise 0.85pt\hbox{$\scriptstyle \smallsetminus $}}} \mathchoice{\hefreshD }{\hefreshD }{\hefreshS }{\hefreshS }\mathbb{R}$
. Thus,
$\zeta _{l^2}\in M \newcommand{\hefreshD }{\mathop{\raise 1.5pt\hbox{${\smallsetminus }$}}} \newcommand{\hefreshS }{\mathop{\raise 0.85pt\hbox{$\scriptstyle \smallsetminus $}}} \mathchoice{\hefreshD }{\hefreshD }{\hefreshS }{\hefreshS }\mathbb{R}$
. Thus,
![]() $M$
cannot be embedded into
$M$
cannot be embedded into
![]() $\mathbb{R}$
, that is
$\mathbb{R}$
, that is
![]() $M$
is totally imaginary. Hence by [Reference Ribes9, p. 302, Thm. 8.8(a)],
$M$
is totally imaginary. Hence by [Reference Ribes9, p. 302, Thm. 8.8(a)],
![]() $\mathrm{cd}_l(\textrm{Gal}(M))\ne \infty$
.
$\mathrm{cd}_l(\textrm{Gal}(M))\ne \infty$
.
Now we consider a prime number
![]() $p$
, a valuation
$p$
, a valuation
![]() $v$
of
$v$
of
![]() $M$
lying over
$M$
lying over
![]() $p$
, and the completion
$p$
, and the completion
![]() ${\hat M}_v$
of
${\hat M}_v$
of
![]() $M$
at
$M$
at
![]() $v$
. Then,
$v$
. Then,
![]() $\zeta _{l^i}\in M\subseteq{\hat M}_v$
for each
$\zeta _{l^i}\in M\subseteq{\hat M}_v$
for each
![]() $i$
. Hence, by Lemma 2.4(b),
$i$
. Hence, by Lemma 2.4(b),
![]() $l^\infty |[{\hat M}_v\;:\;\mathbb{Q}_p]$
. Therefore, by [Reference Ribes9, p. 302, Thm. 8.8(b)],
$l^\infty |[{\hat M}_v\;:\;\mathbb{Q}_p]$
. Therefore, by [Reference Ribes9, p. 302, Thm. 8.8(b)],
![]() $\mathrm{cd}_l(\textrm{Gal}(M))\le 1$
.
$\mathrm{cd}_l(\textrm{Gal}(M))\le 1$
.
Finally, by [Reference Ribes9, p. 217, Cor. 3.2 and p. 221, Prop. 4.4] and [Reference Ribes9, p. 217, Cor. 3.2],
Hence,
![]() $\textrm{Gal}(M)\not \cong \mathbb{Z}_l\times \mathbb{Z}_l$
, as claimed.
$\textrm{Gal}(M)\not \cong \mathbb{Z}_l\times \mathbb{Z}_l$
, as claimed.
Case B:
![]() $K$
is a finite separable extension of
$K$
is a finite separable extension of
![]() $\mathbb{F}_p(t)$
with
$\mathbb{F}_p(t)$
with
![]() $t$
transcendental over
$t$
transcendental over
![]() $\mathbb{F}_p$
. We assume without loss that
$\mathbb{F}_p$
. We assume without loss that
![]() $K=\mathbb{F}_p(t)$
. By assumption,
$K=\mathbb{F}_p(t)$
. By assumption,
![]() $M$
contains the field
$M$
contains the field
![]() $L\;:\!=\;\mathbb{F}_p(\zeta _{l^i})_{i\ge 1}$
, so
$L\;:\!=\;\mathbb{F}_p(\zeta _{l^i})_{i\ge 1}$
, so
![]() $L(t)\subseteq M$
. Since there are infinitely many roots of unity
$L(t)\subseteq M$
. Since there are infinitely many roots of unity
![]() $\zeta _{l^i}$
in
$\zeta _{l^i}$
in
![]() ${\tilde{\mathbb{F}}}_p$
and only finitely many of them belong to each finite field,
${\tilde{\mathbb{F}}}_p$
and only finitely many of them belong to each finite field,
![]() $L$
is an infinite field. In addition, for each
$L$
is an infinite field. In addition, for each
![]() $i\ge 1$
the extension
$i\ge 1$
the extension
![]() $\mathbb{F}_p(\zeta _{l^{i+1}})/\mathbb{F}_p(\zeta _{l^i})$
is cyclic of degree
$\mathbb{F}_p(\zeta _{l^{i+1}})/\mathbb{F}_p(\zeta _{l^i})$
is cyclic of degree
![]() $l$
or trivial. Hence,
$l$
or trivial. Hence,
![]() $\textrm{Gal}(L/\mathbb{F}_p(\zeta _l))\cong \mathbb{Z}_l$
. Therefore,
$\textrm{Gal}(L/\mathbb{F}_p(\zeta _l))\cong \mathbb{Z}_l$
. Therefore,
![]() $L$
is contained in the maximal extension
$L$
is contained in the maximal extension
![]() $L'$
of
$L'$
of
![]() $\mathbb{F}_p(\zeta _l)$
of an
$\mathbb{F}_p(\zeta _l)$
of an
![]() $l$
’th power degree. Since
$l$
’th power degree. Since
![]() $\textrm{Gal}(L'/\mathbb{F}_p(\zeta _l))\cong \mathbb{Z}_l$
, the restriction map
$\textrm{Gal}(L'/\mathbb{F}_p(\zeta _l))\cong \mathbb{Z}_l$
, the restriction map
![]() $\textrm{Gal}(L'/\mathbb{F}_p(\zeta _l))\to \textrm{Gal}(L/\mathbb{F}_p(\zeta _l))$
is surjective, and
$\textrm{Gal}(L'/\mathbb{F}_p(\zeta _l))\to \textrm{Gal}(L/\mathbb{F}_p(\zeta _l))$
is surjective, and
![]() $\mathbb{Z}_l$
is generated by one element, that map is an isomorphism [Reference Fried and Jarden3, p. 331, Cor. 16.10.8]. It follows that
$\mathbb{Z}_l$
is generated by one element, that map is an isomorphism [Reference Fried and Jarden3, p. 331, Cor. 16.10.8]. It follows that
![]() $L=L'$
. Therefore,
$L=L'$
. Therefore,
![]() $l$
does not divide the order of
$l$
does not divide the order of
![]() $\textrm{Gal}(L)$
.
$\textrm{Gal}(L)$
.
By [Reference Ribes9, p. 208, Cor. 2.3],
![]() $\mathrm{cd}_l(\textrm{Gal}(L))=0$
. Hence, by [Reference Ribes9, p. 272, Prop. 5.2],
$\mathrm{cd}_l(\textrm{Gal}(L))=0$
. Hence, by [Reference Ribes9, p. 272, Prop. 5.2],
![]() $\mathrm{cd}_l(\textrm{Gal}(L(t)))=1$
. Since
$\mathrm{cd}_l(\textrm{Gal}(L(t)))=1$
. Since
![]() $\textrm{Gal}(M)\le \textrm{Gal}(L(t))$
, we have by [Reference Ribes9, p. 204, Prop. 2.1(a)], that
$\textrm{Gal}(M)\le \textrm{Gal}(L(t))$
, we have by [Reference Ribes9, p. 204, Prop. 2.1(a)], that
![]() $\mathrm{cd}_l(\textrm{Gal}(M))\le 1$
. As in Case A, this inequality implies that
$\mathrm{cd}_l(\textrm{Gal}(M))\le 1$
. As in Case A, this inequality implies that
![]() $\textrm{Gal}(M)\not \cong \mathbb{Z}_l\times \mathbb{Z}_l$
, as claimed.
$\textrm{Gal}(M)\not \cong \mathbb{Z}_l\times \mathbb{Z}_l$
, as claimed.
Here is the promised result of Geyer.
Theorem 3.3.
Let
![]() $K$
be a global field and
$K$
be a global field and
![]() $A$
a closed abelian subgroup of
$A$
a closed abelian subgroup of
![]() $\textrm{Gal}(K)$
. Then,
$\textrm{Gal}(K)$
. Then,
![]() $A$
is procyclic.
$A$
is procyclic.
Proof. We start the proof with the special case where the torsion group
![]() $A_{\mathrm{tor}}$
of
$A_{\mathrm{tor}}$
of
![]() $A$
is nontrivial. In this case, there exists a non-unit
$A$
is nontrivial. In this case, there exists a non-unit
![]() $\tau \in A$
of finite order. By Lemma 2.2,
$\tau \in A$
of finite order. By Lemma 2.2,
![]() $\mathrm{char}(K)=0$
and
$\mathrm{char}(K)=0$
and
![]() $A\cong \mathbb{Z}/2\mathbb{Z}$
. In particular,
$A\cong \mathbb{Z}/2\mathbb{Z}$
. In particular,
![]() $A$
is procyclic.
$A$
is procyclic.
We may therefore assume that
![]() $A$
is a nontrivial torsion-free abelian profinite group. By Proposition 2.1,
$A$
is a nontrivial torsion-free abelian profinite group. By Proposition 2.1,
![]() $A\cong \prod _l\mathbb{Z}_l^{r_l}$
, where
$A\cong \prod _l\mathbb{Z}_l^{r_l}$
, where
![]() $l$
ranges over all prime numbers and for each
$l$
ranges over all prime numbers and for each
![]() $l$
,
$l$
,
![]() $r_l$
is a cardinal number, so we may assume that
$r_l$
is a cardinal number, so we may assume that
![]() $A\cong \mathbb{Z}_l^r$
for a prime number
$A\cong \mathbb{Z}_l^r$
for a prime number
![]() $l$
and a positive cardinal number
$l$
and a positive cardinal number
![]() $r$
and prove that
$r$
and prove that
![]() $A\cong \mathbb{Z}_l$
.
$A\cong \mathbb{Z}_l$
.
Otherwise,
![]() $A$
contains a closed subgroup which is isomorphic to
$A$
contains a closed subgroup which is isomorphic to
![]() $\mathbb{Z}_l\times \mathbb{Z}_l$
. Thus, we may assume that
$\mathbb{Z}_l\times \mathbb{Z}_l$
. Thus, we may assume that
![]() $A\cong \mathbb{Z}_l\times \mathbb{Z}_l$
and prove that this assumption leads to a contradiction.
$A\cong \mathbb{Z}_l\times \mathbb{Z}_l$
and prove that this assumption leads to a contradiction.
To this end, we denote the fixed field of
![]() $A$
in
$A$
in
![]() $K_{\mathrm{sep}}$
by
$K_{\mathrm{sep}}$
by
![]() $M$
and identify
$M$
and identify
![]() $\textrm{Gal}(M)$
with
$\textrm{Gal}(M)$
with
![]() $A$
. By Lemma 3.1,
$A$
. By Lemma 3.1,
![]() $l\ne \mathrm{char}(K)$
.
$l\ne \mathrm{char}(K)$
.
Claim:
![]() $M$
contains a root of unity
$M$
contains a root of unity
![]() $\zeta _l$
of order
$\zeta _l$
of order
![]() $l$
. Indeed, if
$l$
. Indeed, if
![]() $l=2$
, then
$l=2$
, then
![]() $\zeta _l=-1\in M$
. Otherwise,
$\zeta _l=-1\in M$
. Otherwise,
![]() $l\gt 2$
and if
$l\gt 2$
and if
![]() $\zeta _l\notin M$
, then
$\zeta _l\notin M$
, then
![]() $[M(\zeta _l)\;:\;M]$
is a divisor of
$[M(\zeta _l)\;:\;M]$
is a divisor of
![]() $l-1$
which is greater than
$l-1$
which is greater than
![]() $1$
. On the other hand,
$1$
. On the other hand,
![]() $[M(\zeta _l)\;:\;M]$
divides the (profinite) order of
$[M(\zeta _l)\;:\;M]$
divides the (profinite) order of
![]() $A$
which is
$A$
which is
![]() $l^\infty$
, a contradiction.
$l^\infty$
, a contradiction.
Since
![]() $\textrm{Gal}(M)\cong \mathbb{Z}_l\times \mathbb{Z}_l$
, Lemma 3.2 implies that not all roots of unity of order
$\textrm{Gal}(M)\cong \mathbb{Z}_l\times \mathbb{Z}_l$
, Lemma 3.2 implies that not all roots of unity of order
![]() $l^i$
with
$l^i$
with
![]() $i\ge 1$
belong to
$i\ge 1$
belong to
![]() $M$
. Let
$M$
. Let
![]() $n$
be the smallest positive integer such that
$n$
be the smallest positive integer such that
![]() $M$
contains a root of unity of order
$M$
contains a root of unity of order
![]() $l^{n-1}$
but does not contain a root of unity of order
$l^{n-1}$
but does not contain a root of unity of order
![]() $l^n$
. Choose a root of unity
$l^n$
. Choose a root of unity
![]() $\zeta _{l^n}$
and set
$\zeta _{l^n}$
and set
![]() $M_1=M(\zeta _{l^n})$
. Then,
$M_1=M(\zeta _{l^n})$
. Then,
![]() $\zeta _{l^n}^l\in M$
but
$\zeta _{l^n}^l\in M$
but
![]() $\zeta _{l^n}\notin M$
. Hence,
$\zeta _{l^n}\notin M$
. Hence,
![]() $[M_1\;:\;M]|l$
and
$[M_1\;:\;M]|l$
and
![]() $[M_1\;:\;M]\ne 1$
(by the Claim and [Reference Lang7, p. 289, Thm. 6.2(ii)]), so
$[M_1\;:\;M]\ne 1$
(by the Claim and [Reference Lang7, p. 289, Thm. 6.2(ii)]), so
![]() $[M_1\;:\;M]=l$
.
$[M_1\;:\;M]=l$
.
Let
![]() $U$
be the open subgroup of
$U$
be the open subgroup of
![]() $\mathbb{Z}_l$
of index
$\mathbb{Z}_l$
of index
![]() $l$
. Then, the index of each of the subgroups
$l$
. Then, the index of each of the subgroups
![]() $\mathbb{Z}_l\times U$
and
$\mathbb{Z}_l\times U$
and
![]() $U\times \mathbb{Z}_l$
of
$U\times \mathbb{Z}_l$
of
![]() $\textrm{Gal}(M)$
is
$\textrm{Gal}(M)$
is
![]() $l$
. We choose one of them which is different from
$l$
. We choose one of them which is different from
![]() $\textrm{Gal}(M_1)$
and denote its fixed field in
$\textrm{Gal}(M_1)$
and denote its fixed field in
![]() $K_{\mathrm{sep}}$
by
$K_{\mathrm{sep}}$
by
![]() $M_2$
. Then,
$M_2$
. Then,
![]() $M_2$
is a cyclic extension of
$M_2$
is a cyclic extension of
![]() $M$
of degree
$M$
of degree
![]() $l$
and
$l$
and
![]() $M_1\ne M_2$
.
$M_1\ne M_2$
.
Since
![]() $\zeta _l\in M$
, [Reference Lang7, p. 289, Thm. 6.2(i)] implies the existence of
$\zeta _l\in M$
, [Reference Lang7, p. 289, Thm. 6.2(i)] implies the existence of
![]() $a,x\in K_{\mathrm{sep}}$
with
$a,x\in K_{\mathrm{sep}}$
with
![]() $M_2=M(x)$
and
$M_2=M(x)$
and
![]() $a\;:\!=\;x^l\in M$
. Choose
$a\;:\!=\;x^l\in M$
. Choose
![]() $b\in K_{\mathrm{sep}}$
with
$b\in K_{\mathrm{sep}}$
with
![]() $b^{l^{n-1}}=x$
, so
$b^{l^{n-1}}=x$
, so
![]() $b^{l^n}=a$
. In particular,
$b^{l^n}=a$
. In particular,
![]() $M_2=M(b^{l^{n-1}})\subseteq M(b)$
and
$M_2=M(b^{l^{n-1}})\subseteq M(b)$
and
![]() $[M(b)\;:\;M_2]\le l^{n-1}$
. It follows from the preceding paragraph that
$[M(b)\;:\;M_2]\le l^{n-1}$
. It follows from the preceding paragraph that
Next choose
![]() $\sigma \in A$
such that
$\sigma \in A$
such that
![]() $\sigma |_{M_1}={\mathrm{id}}$
and
$\sigma |_{M_1}={\mathrm{id}}$
and
![]() $\sigma |_{M_2}\ne{\mathrm{id}}$
. In particular,
$\sigma |_{M_2}\ne{\mathrm{id}}$
. In particular,
![]() $\sigma x\ne x$
, so
$\sigma x\ne x$
, so
![]() $\zeta \;:\!=\;(\sigma b)b^{-1}$
satisfies
$\zeta \;:\!=\;(\sigma b)b^{-1}$
satisfies
thus
![]() $\zeta$
is a primitive root of
$\zeta$
is a primitive root of
![]() $1$
of order
$1$
of order
![]() $l^n$
.
$l^n$
.
The definition of
![]() $M_1$
implies that
$M_1$
implies that
![]() $M_1=M(\zeta )$
. But
$M_1=M(\zeta )$
. But
![]() $M(b)$
is a Galois extension of
$M(b)$
is a Galois extension of
![]() $M$
(because
$M$
(because
![]() $\textrm{Gal}(M)$
is abelian). Hence,
$\textrm{Gal}(M)$
is abelian). Hence,
![]() $\zeta =(\sigma b)b^{-1}\in M(b)$
, so
$\zeta =(\sigma b)b^{-1}\in M(b)$
, so
![]() $M_1\subseteq M(b)$
. Since
$M_1\subseteq M(b)$
. Since
![]() $[M_1\;:\;M]=l$
, we have by (3.1) that
$[M_1\;:\;M]=l$
, we have by (3.1) that
![]() $[M(b)\;:\;M_1]\le l^{n-1}$
. Since
$[M(b)\;:\;M_1]\le l^{n-1}$
. Since
![]() $\sigma$
is the identity on
$\sigma$
is the identity on
![]() $M_1$
, the latter inequality implies that
$M_1$
, the latter inequality implies that
![]() ${\mathrm{ord}}(\sigma |_{M(b)})\le l^{n-1}$
.
${\mathrm{ord}}(\sigma |_{M(b)})\le l^{n-1}$
.
On the other hand, the relation
![]() $\sigma b=b\zeta$
implies by induction on
$\sigma b=b\zeta$
implies by induction on
![]() $i$
that
$i$
that
![]() $\sigma ^ib=b\zeta ^i\ne b$
for each
$\sigma ^ib=b\zeta ^i\ne b$
for each
![]() $1\le i\le l^{n-1}$
. Hence,
$1\le i\le l^{n-1}$
. Hence,
![]() ${\mathrm{ord}}(\sigma |_{M(b)})\gt l^{n-1}$
. This contradicts the conclusion of the preceding paragraph, as required.
${\mathrm{ord}}(\sigma |_{M(b)})\gt l^{n-1}$
. This contradicts the conclusion of the preceding paragraph, as required.
4. Generalization of Geyer’s theorem
The central part of the proof of Geyer’s theorem says that for each prime number
![]() $l$
, the largest positive integer
$l$
, the largest positive integer
![]() $n$
for which
$n$
for which
![]() $\mathbb{Z}_l^n$
is a closed subgroup of
$\mathbb{Z}_l^n$
is a closed subgroup of
![]() $\textrm{Gal}(\mathbb{Q})$
or of
$\textrm{Gal}(\mathbb{Q})$
or of
![]() $\textrm{Gal}(\mathbb{F}_p(t))$
is
$\textrm{Gal}(\mathbb{F}_p(t))$
is
![]() $1$
. The next lemma will allow us to generalize that statement to each finitely generated extension of a global field.
$1$
. The next lemma will allow us to generalize that statement to each finitely generated extension of a global field.
Remark 4.1.
Let
![]() $A$
be a finitely generated torsion-free abelian pro-
$A$
be a finitely generated torsion-free abelian pro-
![]() $l$
group for a prime number
$l$
group for a prime number
![]() $l$
. [
Reference Fried and Jarden3, p. 519, Prop. 22.7.12(a)] allows us to also consider
$l$
. [
Reference Fried and Jarden3, p. 519, Prop. 22.7.12(a)] allows us to also consider
![]() $A$
as a finitely generated
$A$
as a finitely generated
![]() $\mathbb{Z}_l$
-module. Since
$\mathbb{Z}_l$
-module. Since
![]() $\mathbb{Z}_l$
is a principal ideal domain, [
Reference Lang7, p. 147, Thm. 7.3] implies that
$\mathbb{Z}_l$
is a principal ideal domain, [
Reference Lang7, p. 147, Thm. 7.3] implies that
![]() $A=\mathbb{Z}_l^n$
is a finitely generated free
$A=\mathbb{Z}_l^n$
is a finitely generated free
![]() $\mathbb{Z}_l$
-module of rank
$\mathbb{Z}_l$
-module of rank
![]() $n$
for some non-negative integer
$n$
for some non-negative integer
![]() $n$
. Since
$n$
. Since
![]() $\mathbb{Z}_l$
is generated, as a profinite group, by one element,
$\mathbb{Z}_l$
is generated, as a profinite group, by one element,
![]() $n$
is also the rank,
$n$
is also the rank,
![]() ${\mathrm{rank}}(A)$
, of
${\mathrm{rank}}(A)$
, of
![]() $A$
as a profinite group. In other words,
$A$
as a profinite group. In other words,
![]() ${\mathrm{rank}}(A)={\mathrm{rank}}_{\mathbb{Z}_l}(A)$
.
${\mathrm{rank}}(A)={\mathrm{rank}}_{\mathbb{Z}_l}(A)$
.
Lemma 4.2.
Let
![]() $K$
be a field,
$K$
be a field,
![]() $t$
an indeterminate, and
$t$
an indeterminate, and
![]() $l$
a prime number. Suppose that
$l$
a prime number. Suppose that
![]() $n$
is the largest positive integer for which
$n$
is the largest positive integer for which
![]() $\mathbb{Z}_l^n$
is a closed subgroup of
$\mathbb{Z}_l^n$
is a closed subgroup of
![]() $\textrm{Gal}(K)$
. Then, the largest positive integer
$\textrm{Gal}(K)$
. Then, the largest positive integer
![]() $m$
for which
$m$
for which
![]() $\mathbb{Z}_l^m$
is a closed subgroup of
$\mathbb{Z}_l^m$
is a closed subgroup of
![]() $\textrm{Gal}(K(t))$
does not exceed
$\textrm{Gal}(K(t))$
does not exceed
![]() $n+1$
.
$n+1$
.
Proof. Suppose that
![]() $A\;:\!=\;\mathbb{Z}_l^{n'}$
is a closed subgroup of
$A\;:\!=\;\mathbb{Z}_l^{n'}$
is a closed subgroup of
![]() $\textrm{Gal}(K(t))$
for some positive integer
$\textrm{Gal}(K(t))$
for some positive integer
![]() $n'$
. Let
$n'$
. Let
![]() $\varphi\;:\;\textrm{Gal}(K(t))\to \textrm{Gal}(K)$
be the restriction map. Then,
$\varphi\;:\;\textrm{Gal}(K(t))\to \textrm{Gal}(K)$
be the restriction map. Then,
![]() ${\mathrm{Ker}}(\varphi )=\textrm{Gal}(K_{\mathrm{sep}}(t))$
. Setting
${\mathrm{Ker}}(\varphi )=\textrm{Gal}(K_{\mathrm{sep}}(t))$
. Setting
![]() ${\bar{A}}=\varphi (A)$
and
${\bar{A}}=\varphi (A)$
and
![]() $A_0={\mathrm{Ker}}(\varphi )\cap A$
, we get the following commutative diagram of profinite groups:
$A_0={\mathrm{Ker}}(\varphi )\cap A$
, we get the following commutative diagram of profinite groups:

where
![]() $\bf 0$
stands for the trivial group of an additive abelian group. Since
$\bf 0$
stands for the trivial group of an additive abelian group. Since
![]() $\mathbb{Z}_l$
is a principal ideal domain and
$\mathbb{Z}_l$
is a principal ideal domain and
![]() $A$
is a free
$A$
is a free
![]() $\mathbb{Z}_l$
-module of rank
$\mathbb{Z}_l$
-module of rank
![]() $n'$
,
$n'$
,
![]() $A_0$
is a free
$A_0$
is a free
![]() $\mathbb{Z}_l$
-module, by [Reference Lang7, p. 146, Thm. 7.1]. Also, by [Reference Lang7, p. 148, Lemma 7.4],
$\mathbb{Z}_l$
-module, by [Reference Lang7, p. 146, Thm. 7.1]. Also, by [Reference Lang7, p. 148, Lemma 7.4],
![]() $\bar{A}$
is a free
$\bar{A}$
is a free
![]() $\mathbb{Z}_l$
-module and
$\mathbb{Z}_l$
-module and
![]() $n'={\mathrm{rank}}(A_0)+{\mathrm{rank}}({\bar{A}})$
.
$n'={\mathrm{rank}}(A_0)+{\mathrm{rank}}({\bar{A}})$
.
By [Reference Ribes9, p. 272, Prop. 5.2],
![]() $\textrm{Gal}(K_{\mathrm{sep}}(t))$
is a projective group, so also
$\textrm{Gal}(K_{\mathrm{sep}}(t))$
is a projective group, so also
![]() $A_0$
is a projective group. In other words,
$A_0$
is a projective group. In other words,
![]() ${\mathrm{rank}}(A_0)\le 1$
. Also, by Corollary 2.3 and the assumption of the lemma,
${\mathrm{rank}}(A_0)\le 1$
. Also, by Corollary 2.3 and the assumption of the lemma,
![]() ${\bar{A}}=\mathbb{Z}_l^m$
with
${\bar{A}}=\mathbb{Z}_l^m$
with
![]() $m\le n$
or
$m\le n$
or
![]() $l=2$
and
$l=2$
and
![]() ${\bar{A}}\cong \mathbb{Z}/2\mathbb{Z}$
. In each case,
${\bar{A}}\cong \mathbb{Z}/2\mathbb{Z}$
. In each case,
![]() ${\mathrm{rank}}({\bar{A}})\le n$
, hence
${\mathrm{rank}}({\bar{A}})\le n$
, hence
![]() ${\mathrm{rank}}(A)={\mathrm{rank}}({\bar{A}})+{\mathrm{rank}}(A_0)\le n+1$
, as claimed.
${\mathrm{rank}}(A)={\mathrm{rank}}({\bar{A}})+{\mathrm{rank}}(A_0)\le n+1$
, as claimed.
Proposition 4.3.
Let
![]() $K$
be a finitely generated extension with transcendence degree
$K$
be a finitely generated extension with transcendence degree
![]() $r$
of a global field
$r$
of a global field
![]() $K_0$
and let
$K_0$
and let
![]() $A$
be a closed abelian subgroup of
$A$
be a closed abelian subgroup of
![]() $\textrm{Gal}(K)$
. Then,
$\textrm{Gal}(K)$
. Then,
![]() $A\cong \mathbb{Z}/2\mathbb{Z}$
or
$A\cong \mathbb{Z}/2\mathbb{Z}$
or
![]() $A\cong \prod _l\mathbb{Z}_l^{r_l}$
, where
$A\cong \prod _l\mathbb{Z}_l^{r_l}$
, where
![]() $l$
ranges over all prime numbers and
$l$
ranges over all prime numbers and
![]() $r_l\le r+1$
for each prime number
$r_l\le r+1$
for each prime number
![]() $l$
.
$l$
.
Proof. By Corollary 2.3,
![]() $A\cong \mathbb{Z}/2\mathbb{Z}$
or
$A\cong \mathbb{Z}/2\mathbb{Z}$
or
![]() $A\cong \prod _l\mathbb{Z}_l^{r_l}$
, with cardinal numbers
$A\cong \prod _l\mathbb{Z}_l^{r_l}$
, with cardinal numbers
![]() $r_l$
. Assume the latter case. If
$r_l$
. Assume the latter case. If
![]() $K$
is a global field, then
$K$
is a global field, then
![]() $r=0$
. Hence, by Theorem 3.3,
$r=0$
. Hence, by Theorem 3.3,
![]() $r_l\le 0+1$
for each
$r_l\le 0+1$
for each
![]() $l$
.
$l$
.
Otherwise,
![]() $r\ge 1$
and
$r\ge 1$
and
![]() $K$
is a finitely generated extension of transcendence degree
$K$
is a finitely generated extension of transcendence degree
![]() $1$
of a finitely generated extension
$1$
of a finitely generated extension
![]() $K'_0$
of transcendence degree
$K'_0$
of transcendence degree
![]() $r-1$
of
$r-1$
of
![]() $K_0$
. By induction, for each prime number
$K_0$
. By induction, for each prime number
![]() $l$
,
$l$
,
![]() $r$
is the largest positive integer such that
$r$
is the largest positive integer such that
![]() $\mathbb{Z}_l^r$
is a closed subgroup of
$\mathbb{Z}_l^r$
is a closed subgroup of
![]() $\textrm{Gal}(K'_0)$
. Hence, by Lemma 4.2,
$\textrm{Gal}(K'_0)$
. Hence, by Lemma 4.2,
![]() $r+1$
is the largest positive number for which
$r+1$
is the largest positive number for which
![]() $\mathbb{Z}_l^{r+1}$
is a closed subgroup of
$\mathbb{Z}_l^{r+1}$
is a closed subgroup of
![]() $\textrm{Gal}(K)$
. In particular,
$\textrm{Gal}(K)$
. In particular,
![]() $r_l\le r+1$
, as claimed.
$r_l\le r+1$
, as claimed.
5. Realizing
 ${\hat{\mathbb{Z}}}^{r+1}$
as a closed subgroup of
${\hat{\mathbb{Z}}}^{r+1}$
as a closed subgroup of
 $\textrm{Gal}(K)$
$\textrm{Gal}(K)$
Let
![]() $K$
be a finitely generated extension of
$K$
be a finitely generated extension of
![]() $\mathbb{Q}$
of transcendence degree
$\mathbb{Q}$
of transcendence degree
![]() $r$
. We complete Proposition 4.3 in this section by proving that
$r$
. We complete Proposition 4.3 in this section by proving that
![]() ${\hat{\mathbb{Z}}}^{r+1}$
is a closed subgroup of
${\hat{\mathbb{Z}}}^{r+1}$
is a closed subgroup of
![]() $\textrm{Gal}(K)$
. An analogous result holds for a finitely generated extension
$\textrm{Gal}(K)$
. An analogous result holds for a finitely generated extension
![]() $K$
of transcendence degree
$K$
of transcendence degree
![]() $r$
of
$r$
of
![]() $\mathbb{F}_p(t)$
, in which case
$\mathbb{F}_p(t)$
, in which case
![]() $\prod _{l\ne p}\mathbb{Z}_l^{r+1}$
replaces
$\prod _{l\ne p}\mathbb{Z}_l^{r+1}$
replaces
![]() ${\hat{\mathbb{Z}}}^{r+1}$
.
${\hat{\mathbb{Z}}}^{r+1}$
.
Remark 5.1 (Valued fields). We denote the residue field of a valued field
![]() $(F,v)$
by
$(F,v)$
by
![]() ${\bar{F}}_v$
and its value group by
${\bar{F}}_v$
and its value group by
![]() $v(F^\times )$
. In addition, we extend
$v(F^\times )$
. In addition, we extend
![]() $v$
to a valuation of
$v$
to a valuation of
![]() $F_{\mathrm{sep}}$
that we also denote by
$F_{\mathrm{sep}}$
that we also denote by
![]() $v$
, consider its valuation ring
$v$
, consider its valuation ring
![]() $O_{v,\mathrm{sep}}$
, and let
$O_{v,\mathrm{sep}}$
, and let
![]() $D_{v,\mathrm{sep}}=\{\sigma \in \textrm{Gal}(F)\mathop{|\;}\sigma O_{v,\mathrm{sep}}=O_{v,\mathrm{sep}}\}$
be the corresponding
decomposition group
. Then, we let
$D_{v,\mathrm{sep}}=\{\sigma \in \textrm{Gal}(F)\mathop{|\;}\sigma O_{v,\mathrm{sep}}=O_{v,\mathrm{sep}}\}$
be the corresponding
decomposition group
. Then, we let
![]() $F_v$
be the fixed field of
$F_v$
be the fixed field of
![]() $D_{v,\mathrm{sep}}$
in
$D_{v,\mathrm{sep}}$
in
![]() $F_{\mathrm{sep}}$
. Abusing our notation, we also let
$F_{\mathrm{sep}}$
. Abusing our notation, we also let
![]() $v$
be the restriction of
$v$
be the restriction of
![]() $v$
to
$v$
to
![]() $F_v$
. Then,
$F_v$
. Then,
![]() $(F_v,v)$
is the
Henselization
of
$(F_v,v)$
is the
Henselization
of
![]() $(F,v)$
.
$(F,v)$
.
One knows that
![]() $(F_v,v)$
has the same residue field and value group as those of
$(F_v,v)$
has the same residue field and value group as those of
![]() $(F,v)$
[
Reference Efrat2, p. 138, Prop. 15.3.7]. Moreover, the valued fields
$(F,v)$
[
Reference Efrat2, p. 138, Prop. 15.3.7]. Moreover, the valued fields
![]() $(F_{\mathrm{sep}},v)$
and
$(F_{\mathrm{sep}},v)$
and
![]() $(F_v,v)$
depend on the extension of
$(F_v,v)$
depend on the extension of
![]() $v$
to
$v$
to
![]() $F_{\mathrm{sep}}$
up to isomorphism [
Reference Efrat2, p. 138, Cor. 15.3.6].
$F_{\mathrm{sep}}$
up to isomorphism [
Reference Efrat2, p. 138, Cor. 15.3.6].
If
![]() $v$
is a rank-
$v$
is a rank-
![]() $1$
valuation, then so is its extension to
$1$
valuation, then so is its extension to
![]() $F_v$
. In this case, the completion
$F_v$
. In this case, the completion
![]() $({\hat F}_v,v)$
of
$({\hat F}_v,v)$
of
![]() $(F,v)$
is also discrete with the same value group and residue field as those of
$(F,v)$
is also discrete with the same value group and residue field as those of
![]() $(F,v)$
. Moreover,
$(F,v)$
. Moreover,
![]() $({\hat F}_v,v)$
is also the completion of
$({\hat F}_v,v)$
is also the completion of
![]() $(F_v,v)$
. By Hensel’s lemma,
$(F_v,v)$
. By Hensel’s lemma,
![]() $({\hat F}_v,v)$
is also Henselian [
Reference Efrat2, p. 167, Cor. 18.3.2]. We embed
$({\hat F}_v,v)$
is also Henselian [
Reference Efrat2, p. 167, Cor. 18.3.2]. We embed
![]() $F_{\mathrm{sep}}$
into
$F_{\mathrm{sep}}$
into
![]() ${\hat F}_{v,\mathrm{sep}}$
and observe that
${\hat F}_{v,\mathrm{sep}}$
and observe that
![]() $F_{\mathrm{sep}}\cap{\hat F}_v=F_v$
(since
$F_{\mathrm{sep}}\cap{\hat F}_v=F_v$
(since
![]() $(F_{\mathrm{sep}}\cap{\hat F}_v,v)$
is an immediate separable algebraic extension of
$(F_{\mathrm{sep}}\cap{\hat F}_v,v)$
is an immediate separable algebraic extension of
![]() $(F_v,v)$
) and
$(F_v,v)$
) and
![]() $F_{\mathrm{sep}}{\hat F}_v={\hat F}_{v,\mathrm{sep}}$
(by the Krasner-Ostrowski lemma [
Reference Efrat2, p. 172, Cor. 18.5.3]). Thus, restriction gives an isomorphism
$F_{\mathrm{sep}}{\hat F}_v={\hat F}_{v,\mathrm{sep}}$
(by the Krasner-Ostrowski lemma [
Reference Efrat2, p. 172, Cor. 18.5.3]). Thus, restriction gives an isomorphism
![]() $\textrm{Gal}({\hat F}_v)\cong \textrm{Gal}(F_v)$
of the corresponding absolute Galois groups.
$\textrm{Gal}({\hat F}_v)\cong \textrm{Gal}(F_v)$
of the corresponding absolute Galois groups.
We denote the maximal unramified extension of
![]() $F_v$
(resp.
$F_v$
(resp.
![]() ${\hat F}_v$
) by
${\hat F}_v$
) by
![]() $F_{v,\mathrm{ur}}$
(resp.
$F_{v,\mathrm{ur}}$
(resp.
![]() ${\hat F}_{v,\mathrm{ur}}$
) and the maximal tamely ramified extension by
${\hat F}_{v,\mathrm{ur}}$
) and the maximal tamely ramified extension by
![]() $F_{v,{\mathrm{tr}}}$
(resp.
$F_{v,{\mathrm{tr}}}$
(resp.
![]() ${\hat F}_{v,{\mathrm{tr}}}$
). These fields are Galois extensions of
${\hat F}_{v,{\mathrm{tr}}}$
). These fields are Galois extensions of
![]() $F_v$
(resp.
$F_v$
(resp.
![]() ${\hat F}_v$
). As in [
Reference Efrat2, p. 133, p. 141, and p. 145], we set
${\hat F}_v$
). As in [
Reference Efrat2, p. 133, p. 141, and p. 145], we set
![]() $Z(v)=\textrm{Gal}(F_v)$
for the
decomposition group
,
$Z(v)=\textrm{Gal}(F_v)$
for the
decomposition group
,
![]() $T(v)=\textrm{Gal}(F_{v,\mathrm{ur}})$
for the
inertia group
, and
$T(v)=\textrm{Gal}(F_{v,\mathrm{ur}})$
for the
inertia group
, and
![]() $V(v)=\textrm{Gal}(F_{v,{\mathrm{tr}}})$
for the
ramification group
of
$V(v)=\textrm{Gal}(F_{v,{\mathrm{tr}}})$
for the
ramification group
of
![]() $(F,v)$
. The letters
$(F,v)$
. The letters
![]() $Z$
,
$Z$
,
![]() $T$
, and
$T$
, and
![]() $V$
are borrowed from the German translations Zerlegsungruppe, Trägheitsgruppe, and Verzweigungsgruppe of the English expressions decomposition group, inertia group, and ramification group,
$V$
are borrowed from the German translations Zerlegsungruppe, Trägheitsgruppe, and Verzweigungsgruppe of the English expressions decomposition group, inertia group, and ramification group,

Each of the fields
![]() $F_{v,\mathrm{ur}}$
,
$F_{v,\mathrm{ur}}$
,
![]() $F_{v,{\mathrm{tr}}}$
, and
$F_{v,{\mathrm{tr}}}$
, and
![]() $F_{\mathrm{sep}}$
is a Galois extension of
$F_{\mathrm{sep}}$
is a Galois extension of
![]() $F_v$
. By [
Reference Efrat2, p. 199, Thm. 22.1.1] and [
Reference Kuhlmann, Pank and Roquette6, Thm. 2.2] (resp. [
Reference Efrat2, p. 203, Thm. 22.2.1]) both restriction maps
$F_v$
. By [
Reference Efrat2, p. 199, Thm. 22.1.1] and [
Reference Kuhlmann, Pank and Roquette6, Thm. 2.2] (resp. [
Reference Efrat2, p. 203, Thm. 22.2.1]) both restriction maps
split. In particular, each closed subgroup of
![]() $\textrm{Gal}(F_{v,\mathrm{ur}}/F_v)$
; hence, each closed subgroup of
$\textrm{Gal}(F_{v,\mathrm{ur}}/F_v)$
; hence, each closed subgroup of
![]() $\textrm{Gal}({\bar{F}}_v)$
is isomorphic to a closed subgroup of
$\textrm{Gal}({\bar{F}}_v)$
is isomorphic to a closed subgroup of
![]() $\textrm{Gal}(F_{v,{\mathrm{tr}}}/F_v)$
. Also, each closed subgroup of
$\textrm{Gal}(F_{v,{\mathrm{tr}}}/F_v)$
. Also, each closed subgroup of
![]() $\textrm{Gal}(F_{v,{\mathrm{tr}}}/F_v)$
is isomorphic to a closed subgroup of
$\textrm{Gal}(F_{v,{\mathrm{tr}}}/F_v)$
is isomorphic to a closed subgroup of
![]() $\textrm{Gal}(F_v)$
.
$\textrm{Gal}(F_v)$
.
Note that
![]() $E$
in Theorem 22.1.1 of [Reference Efrat2] is
$E$
in Theorem 22.1.1 of [Reference Efrat2] is
![]() $F_{\mathrm{sep}}$
, in our notation, so it satisfies the condition
$F_{\mathrm{sep}}$
, in our notation, so it satisfies the condition
![]() $E=E^l$
for all prime numbers
$E=E^l$
for all prime numbers
![]() $l\ne \mathrm{char}({\bar{F}}_v)$
needed in that theorem.
$l\ne \mathrm{char}({\bar{F}}_v)$
needed in that theorem.
Notation 5.2.
We denote the group of roots of unity in a field
![]() $F$
by
$F$
by
![]() $\mu (F)$
. If
$\mu (F)$
. If
![]() $\mathrm{char}(F)=p\gt 0$
and
$\mathrm{char}(F)=p\gt 0$
and
![]() $F$
is separably closed, then
$F$
is separably closed, then
![]() $\mu (F)={\tilde{\mathbb{F}}}_p^\times$
. If
$\mu (F)={\tilde{\mathbb{F}}}_p^\times$
. If
![]() $\mathrm{char}(F)=0$
and
$\mathrm{char}(F)=0$
and
![]() $F$
is algebraically closed, then
$F$
is algebraically closed, then
![]() $\mu (F)=\mu ({\tilde{\mathbb{Q}}})$
and
$\mu (F)=\mu ({\tilde{\mathbb{Q}}})$
and
![]() $\mathbb{Q}_{\mathrm{ab}}\;:\!=\;\mathbb{Q}(\mu ({\tilde{\mathbb{Q}}}))$
is the maximal abelian extension of
$\mathbb{Q}_{\mathrm{ab}}\;:\!=\;\mathbb{Q}(\mu ({\tilde{\mathbb{Q}}}))$
is the maximal abelian extension of
![]() $\mathbb{Q}$
(by the theorem of Kronecker–Weber [
Reference Neukirch8, p. 324, Thm. 110]).
$\mathbb{Q}$
(by the theorem of Kronecker–Weber [
Reference Neukirch8, p. 324, Thm. 110]).
Remark 5.3.
Given a field
![]() $K$
, the
field of formal power series
$K$
, the
field of formal power series
![]() $K((t))$
in the variable
$K((t))$
in the variable
![]() $t$
with coefficients in
$t$
with coefficients in
![]() $K$
, also called the
field of Laurent series over
$K$
, also called the
field of Laurent series over
![]() $K$
, is the field of all formal power series
$K$
, is the field of all formal power series
![]() $\sum _{i=m}^\infty a_it^i$
with
$\sum _{i=m}^\infty a_it^i$
with
![]() $m\in \mathbb{Z}$
and
$m\in \mathbb{Z}$
and
![]() $a_i\in K$
for all
$a_i\in K$
for all
![]() $i\ge m$
. If
$i\ge m$
. If
![]() $l\lt m$
, then
$l\lt m$
, then
![]() $\sum _{i=m}^\infty a_it^i$
is identified with
$\sum _{i=m}^\infty a_it^i$
is identified with
![]() $\sum _{i=l}^\infty a_it^i$
with
$\sum _{i=l}^\infty a_it^i$
with
![]() $a_i=0$
for each
$a_i=0$
for each
![]() $l\le i\lt m$
. Summation and multiplication in
$l\le i\lt m$
. Summation and multiplication in
![]() $K((t))$
are defined by the following rules:
$K((t))$
are defined by the following rules:
 \begin{align*} \begin{aligned} \sum _{i=m}^\infty a_it^i +\sum _{i=m'}^\infty a'_it^i &=\sum _{i=\min (m,m')}^\infty (a_i+a'_i)t^i, \cr \big (\sum _{i=m}^\infty a_it^i\big ) \big (\sum _{j=m'}^\infty a'_jt^j\big ) &=\sum _{k=m+m'}^\infty \big (\sum _{i+j=k}a_ia'_j)t^k. \end{aligned} \end{align*}
\begin{align*} \begin{aligned} \sum _{i=m}^\infty a_it^i +\sum _{i=m'}^\infty a'_it^i &=\sum _{i=\min (m,m')}^\infty (a_i+a'_i)t^i, \cr \big (\sum _{i=m}^\infty a_it^i\big ) \big (\sum _{j=m'}^\infty a'_jt^j\big ) &=\sum _{k=m+m'}^\infty \big (\sum _{i+j=k}a_ia'_j)t^k. \end{aligned} \end{align*}
Let
![]() $v$
be the unique discrete valuation of
$v$
be the unique discrete valuation of
![]() $K(t)$
with
$K(t)$
with
![]() $v(a)=0$
for each
$v(a)=0$
for each
![]() $a\in K$
and
$a\in K$
and
![]() $v(t)=1$
. Then,
$v(t)=1$
. Then,
![]() $(K((t)),v)$
is the completion of
$(K((t)),v)$
is the completion of
![]() $(K(t),v)$
, where
$(K(t),v)$
, where
![]() $v(\sum _{i=m}^\infty a_it^i)=m$
whenever
$v(\sum _{i=m}^\infty a_it^i)=m$
whenever
![]() $a_m\ne 0$
. By [
Reference Efrat2, p. 167, Cor. 18.3.2],
$a_m\ne 0$
. By [
Reference Efrat2, p. 167, Cor. 18.3.2],
![]() $K((t))$
is Henselian with respect to
$K((t))$
is Henselian with respect to
![]() $v$
.
$v$
.
By [ Reference Cassels and Fröhlich1, p. 28, Cor. 2] (or [ Reference Efrat2, p. 141, Thm. 16.1.1]),
Replacing
![]() $K$
by
$K$
by
![]() $K_{\mathrm{sep}}$
, we have that
$K_{\mathrm{sep}}$
, we have that
![]() $K_{\mathrm{sep}}((t))_{\mathrm{ur}}=K_{\mathrm{sep}}((t))$
. Since the roots of unity of order
$K_{\mathrm{sep}}((t))_{\mathrm{ur}}=K_{\mathrm{sep}}((t))$
. Since the roots of unity of order
![]() $n$
with
$n$
with
![]() $\mathrm{char}(K)\nmid n$
are in
$\mathrm{char}(K)\nmid n$
are in
![]() $K_{\mathrm{sep}}$
, we have that
$K_{\mathrm{sep}}$
, we have that
![]() $K_{\mathrm{sep}}((t))$
has a cyclic extension of degree
$K_{\mathrm{sep}}((t))$
has a cyclic extension of degree
![]() $n$
in
$n$
in
![]() $K_{\mathrm{sep}}((t))_{\mathrm{tr}}$
. Indeed, that extension is
$K_{\mathrm{sep}}((t))_{\mathrm{tr}}$
. Indeed, that extension is
![]() $K_{\mathrm{sep}}((t^{1/n}))$
.
$K_{\mathrm{sep}}((t^{1/n}))$
.
Going to the limit of these extensions, we obtain with
![]() $p\;:\!=\;\mathrm{char}(K)$
that
$p\;:\!=\;\mathrm{char}(K)$
that
![]() $K_{\mathrm{sep}}((t))_{\mathrm{tr}} =\bigcup _{p\nmid n}K_{\mathrm{sep}}((t^{1/n}))$
and
$K_{\mathrm{sep}}((t))_{\mathrm{tr}} =\bigcup _{p\nmid n}K_{\mathrm{sep}}((t^{1/n}))$
and
![]() $\textrm{Gal}(K_{\mathrm{sep}}((t))_{\mathrm{tr}}/K_{\mathrm{sep}}((t))) \cong \prod _{l\ne p}\mathbb{Z}_l$
.
$\textrm{Gal}(K_{\mathrm{sep}}((t))_{\mathrm{tr}}/K_{\mathrm{sep}}((t))) \cong \prod _{l\ne p}\mathbb{Z}_l$
.
Moreover, if
![]() $\mathrm{char}(K)=0$
, then the ramification group
$\mathrm{char}(K)=0$
, then the ramification group
![]() $\textrm{Gal}({\tilde{K}}((t))_{\mathrm{tr}})$
of
$\textrm{Gal}({\tilde{K}}((t))_{\mathrm{tr}})$
of
![]() ${\tilde{K}}((t))$
is trivial [
Reference Efrat2, p. 145, Thm. 16.2.3], so
${\tilde{K}}((t))$
is trivial [
Reference Efrat2, p. 145, Thm. 16.2.3], so
![]() ${\tilde{K}}((t))_{\mathrm{tr}}=\widetilde{K((t))}$
. Thus, by the preceding paragraph, in this case,
${\tilde{K}}((t))_{\mathrm{tr}}=\widetilde{K((t))}$
. Thus, by the preceding paragraph, in this case,
![]() $\textrm{Gal}({\tilde{K}}((t)))\cong{\hat{\mathbb{Z}}}$
.
$\textrm{Gal}({\tilde{K}}((t)))\cong{\hat{\mathbb{Z}}}$
.
Lemma 5.4.
Let
![]() $K_0$
be a field of characteristic
$K_0$
be a field of characteristic
![]() $p$
,
$p$
,
![]() $t$
an indeterminate, and
$t$
an indeterminate, and
![]() $r$
a positive integer. Suppose that
$r$
a positive integer. Suppose that
![]() $\mu (K_{0,\mathrm{sep}})\subseteq K_0$
and
$\mu (K_{0,\mathrm{sep}})\subseteq K_0$
and
![]() $\prod _{l\ne p}\mathbb{Z}_l^r$
is a closed subgroup of
$\prod _{l\ne p}\mathbb{Z}_l^r$
is a closed subgroup of
![]() $\textrm{Gal}(K_0)$
. Then,
$\textrm{Gal}(K_0)$
. Then,
![]() $\prod _{l\ne p}\mathbb{Z}_l^{r+1}$
is a closed subgroup of
$\prod _{l\ne p}\mathbb{Z}_l^{r+1}$
is a closed subgroup of
![]() $\textrm{Gal}(K_0(t))$
.
$\textrm{Gal}(K_0(t))$
.
Proof. By assumption, the field
![]() $K_0$
has a separable algebraic extension
$K_0$
has a separable algebraic extension
![]() $K$
with
$K$
with
![]() $\textrm{Gal}(K)\cong \prod _{l\ne p}\mathbb{Z}_l^r$
. Let
$\textrm{Gal}(K)\cong \prod _{l\ne p}\mathbb{Z}_l^r$
. Let
![]() $v$
be the discrete
$v$
be the discrete
![]() $K$
-valuation of
$K$
-valuation of
![]() $K(t)$
with
$K(t)$
with
![]() $v(t)=1$
and choose a Henselization
$v(t)=1$
and choose a Henselization
![]() $M\;:\!=\;K(t)_v$
of
$M\;:\!=\;K(t)_v$
of
![]() $K(t)$
with respect to
$K(t)$
with respect to
![]() $v$
. Then,
$v$
. Then,
is the residue field of both
![]() $K(t)$
and
$K(t)$
and
![]() $M$
with respect to
$M$
with respect to
![]() $v$
.
$v$
.
Claim:
![]() $M$
is linearly disjoint from
$M$
is linearly disjoint from
![]() $\tilde{K}$
over
$\tilde{K}$
over
![]() $K$
. Indeed, let
$K$
. Indeed, let
![]() ${\tilde{K}}_1,\ldots,{\tilde{K}}_n$
be linearly independent elements of
${\tilde{K}}_1,\ldots,{\tilde{K}}_n$
be linearly independent elements of
![]() $\tilde{K}$
over
$\tilde{K}$
over
![]() $K$
. Assume toward contradiction that there exist
$K$
. Assume toward contradiction that there exist
![]() $m_1,\ldots,m_n\in M$
not all zero with
$m_1,\ldots,m_n\in M$
not all zero with
![]() $\sum _{i=1}^nm_i{\tilde{K}}_i=0$
. Dividing
$\sum _{i=1}^nm_i{\tilde{K}}_i=0$
. Dividing
![]() $m_1,\ldots,m_n$
by the element with the least
$m_1,\ldots,m_n$
by the element with the least
![]() $v$
-value, we may assume that the
$v$
-value, we may assume that the
![]() $v$
-residues
$v$
-residues
![]() ${\bar m}_1,\ldots,{\bar m}_n$
are elements of
${\bar m}_1,\ldots,{\bar m}_n$
are elements of
![]() $K$
and one of them is non-zero. Thus,
$K$
and one of them is non-zero. Thus,
![]() $\Sigma _{i=1}^n{\bar m}_i{\tilde{K}}_i=0$
, contradicting the assumption on
$\Sigma _{i=1}^n{\bar m}_i{\tilde{K}}_i=0$
, contradicting the assumption on
![]() ${\tilde{K}}_1,\ldots,{\tilde{K}}_n$
. This proves our claim.
${\tilde{K}}_1,\ldots,{\tilde{K}}_n$
. This proves our claim.
By [Reference Efrat2, p. 200, Cor. 22.1.2],
where
![]() $Z(v)=\textrm{Gal}(M)$
and
$Z(v)=\textrm{Gal}(M)$
and
![]() $V(v)$
are respectively the corresponding decomposition and the ramification groups of
$V(v)$
are respectively the corresponding decomposition and the ramification groups of
![]() $M$
and
$M$
and
See [Reference Efrat2, last line of page 144] with
![]() $\bar \mu$
in that line being
$\bar \mu$
in that line being
![]() $\mu (K_{0,\mathrm{sep}})$
, as introduced in the first paragraph of [Reference Efrat2, p. 143, Sec. 16.2].
$\mu (K_{0,\mathrm{sep}})$
, as introduced in the first paragraph of [Reference Efrat2, p. 143, Sec. 16.2].
The action of
![]() $\textrm{Gal}(K)$
on
$\textrm{Gal}(K)$
on
![]() $\chi (v)$
is given for each
$\chi (v)$
is given for each
![]() $\tau \in \textrm{Gal}(K)$
, each homomorphism
$\tau \in \textrm{Gal}(K)$
, each homomorphism
![]() $h\;:\; v(M_{\mathrm{sep}}^\times )/v(M^\times ) \to \mu (K_{0,\mathrm{sep}})$
, and every
$h\;:\; v(M_{\mathrm{sep}}^\times )/v(M^\times ) \to \mu (K_{0,\mathrm{sep}})$
, and every
![]() $\gamma \in v(M_{\mathrm{sep}}^\times )$
, by
$\gamma \in v(M_{\mathrm{sep}}^\times )$
, by
where the latter equality holds because
![]() $\mu (K_{0,\mathrm{sep}})\subseteq K_0\subseteq K$
. In other words, that action is trivial. It follows that
$\mu (K_{0,\mathrm{sep}})\subseteq K_0\subseteq K$
. In other words, that action is trivial. It follows that
By [Reference Efrat2, p. 147, Cor. 16.2.7], there is a short exact sequence
Hence,
![]() $\chi (v)\cong T(v)/V(v)$
.
$\chi (v)\cong T(v)/V(v)$
.
By our choice of
![]() $v$
, the completion of
$v$
, the completion of
![]() $K(t)$
with respect to
$K(t)$
with respect to
![]() $v$
(which is also the completion of the Henselian field
$v$
(which is also the completion of the Henselian field
![]() $M$
) is the field
$M$
) is the field
![]() $K((t))$
of formal power series in
$K((t))$
of formal power series in
![]() $t$
with coefficients in
$t$
with coefficients in
![]() $K$
[Reference Efrat2, p. 83, Example 9.2.2]. The maximal unramified extension of
$K$
[Reference Efrat2, p. 83, Example 9.2.2]. The maximal unramified extension of
![]() $K((t))$
is
$K((t))$
is
![]() $K_{\mathrm{sep}}((t))$
and by Remark 5.3,
$K_{\mathrm{sep}}((t))$
and by Remark 5.3,
![]() $\chi (v)\cong T(v)/V(v) \cong \textrm{Gal}(M_{\mathrm{tr}}/M_{\mathrm{ur}})\cong \prod _{l\ne p}\mathbb{Z}_l$
.
$\chi (v)\cong T(v)/V(v) \cong \textrm{Gal}(M_{\mathrm{tr}}/M_{\mathrm{ur}})\cong \prod _{l\ne p}\mathbb{Z}_l$
.
By the definition of
![]() $K$
,
$K$
,
![]() $\textrm{Gal}(K)\cong \prod _{l\ne p}\mathbb{Z}_l^r$
. Hence, by the preceding paragraph,
$\textrm{Gal}(K)\cong \prod _{l\ne p}\mathbb{Z}_l^r$
. Hence, by the preceding paragraph,
Since by [Reference Kuhlmann, Pank and Roquette6, Thm. 2.2], the epimorphism
![]() $\textrm{Gal}(M)\to \textrm{Gal}(M_{\mathrm{tr}}/M)$
splits,
$\textrm{Gal}(M)\to \textrm{Gal}(M_{\mathrm{tr}}/M)$
splits,
![]() $\prod _{l\ne p}\mathbb{Z}_l^{r+1}$
is a closed subgroup of
$\prod _{l\ne p}\mathbb{Z}_l^{r+1}$
is a closed subgroup of
![]() $\textrm{Gal}(M)$
. Since
$\textrm{Gal}(M)$
. Since
![]() $M$
is a separable algebraic extension of
$M$
is a separable algebraic extension of
![]() $K_0(t)$
[Reference Efrat2, p. 137, Thm. 15.3.5],
$K_0(t)$
[Reference Efrat2, p. 137, Thm. 15.3.5],
![]() $\prod _{l\ne p}\mathbb{Z}_l^{r+1}$
is also a closed subgroup of
$\prod _{l\ne p}\mathbb{Z}_l^{r+1}$
is also a closed subgroup of
![]() $\textrm{Gal}(K_0(t))$
, as claimed.
$\textrm{Gal}(K_0(t))$
, as claimed.
Remark 5.5.
Note that the references that support both (5.3) and (5.4) hold also in the case where
![]() $\mathrm{char}(K_0)=0$
.
$\mathrm{char}(K_0)=0$
.
The following result will be needed in Theorem 5.7.
Lemma 5.6.
Let
![]() $L$
be a set of prime numbers and
$L$
be a set of prime numbers and
![]() $H$
an open subgroup of
$H$
an open subgroup of
![]() $\prod _{l\in L}\mathbb{Z}_l$
. Then,
$\prod _{l\in L}\mathbb{Z}_l$
. Then,
![]() $H\cong \prod _{l\in L}\mathbb{Z}_l$
.
$H\cong \prod _{l\in L}\mathbb{Z}_l$
.
Proof. We set
![]() $Z\;:\!=\;\prod _{l\in L}\mathbb{Z}_l$
and consider all the groups appearing in this proof as additive groups. Since
$Z\;:\!=\;\prod _{l\in L}\mathbb{Z}_l$
and consider all the groups appearing in this proof as additive groups. Since
![]() $H$
is open in
$H$
is open in
![]() $Z$
, its index
$Z$
, its index
![]() $n\;:\!=\;(Z\;:\;H)$
is a positive integer. Since
$n\;:\!=\;(Z\;:\;H)$
is a positive integer. Since
![]() $Z$
is abelian,
$Z$
is abelian,
![]() $H$
is normal in
$H$
is normal in
![]() $Z$
, so
$Z$
, so
![]() $nZ\le H$
$nZ\le H$
By [Reference Fried and Jarden3, p. 13, Lemma 1.4.2(e)],
![]() $n\mathbb{Z}_l\cong \mathbb{Z}_l$
for each
$n\mathbb{Z}_l\cong \mathbb{Z}_l$
for each
![]() $l\in L$
. Hence,
$l\in L$
. Hence,
![]() $nZ=\prod _{l\in L}n\mathbb{Z}_l \cong \prod _{l\in L}\mathbb{Z}_l=Z$
.
$nZ=\prod _{l\in L}n\mathbb{Z}_l \cong \prod _{l\in L}\mathbb{Z}_l=Z$
.
Let
![]() $n=\prod _{l\in L'}l^{i(l)}$
be the decomposition of
$n=\prod _{l\in L'}l^{i(l)}$
be the decomposition of
![]() $n$
into a product of prime powers. If
$n$
into a product of prime powers. If
![]() $l$
and
$l$
and
![]() $l'$
are distinct prime numbers, then
$l'$
are distinct prime numbers, then
![]() $l'$
is a unit of the ring
$l'$
is a unit of the ring
![]() $\mathbb{Z}_l$
, so
$\mathbb{Z}_l$
, so
![]() $l'\mathbb{Z}_l=\mathbb{Z}_l$
. Hence,
$l'\mathbb{Z}_l=\mathbb{Z}_l$
. Hence,
![]() $nZ=\prod _{l\in L\cap L'}l^{i(l)}\mathbb{Z}_l \times \prod _{l\in L \newcommand{\hefreshD }{\mathop{\raise 1.5pt\hbox{${\smallsetminus }$}}} \newcommand{\hefreshS }{\mathop{\raise 0.85pt\hbox{$\scriptstyle \smallsetminus $}}} \mathchoice{\hefreshD }{\hefreshD }{\hefreshS }{\hefreshS } L'}\mathbb{Z}_l$
. Therefore,
$nZ=\prod _{l\in L\cap L'}l^{i(l)}\mathbb{Z}_l \times \prod _{l\in L \newcommand{\hefreshD }{\mathop{\raise 1.5pt\hbox{${\smallsetminus }$}}} \newcommand{\hefreshS }{\mathop{\raise 0.85pt\hbox{$\scriptstyle \smallsetminus $}}} \mathchoice{\hefreshD }{\hefreshD }{\hefreshS }{\hefreshS } L'}\mathbb{Z}_l$
. Therefore,
![]() $(Z\;:\;nZ) =\prod _{l\in L\cap L'}(\mathbb{Z}_l\;:\;l^{i(l)}\mathbb{Z}_l) =\prod _{l\in L\cap L'}l^{i(l)} \le n =(Z\;:\;H)$
. Combining this result with the result of the first paragraph of the proof, we have
$(Z\;:\;nZ) =\prod _{l\in L\cap L'}(\mathbb{Z}_l\;:\;l^{i(l)}\mathbb{Z}_l) =\prod _{l\in L\cap L'}l^{i(l)} \le n =(Z\;:\;H)$
. Combining this result with the result of the first paragraph of the proof, we have
![]() $H=nZ$
. Therefore, by the second paragraph of the proof,
$H=nZ$
. Therefore, by the second paragraph of the proof,
![]() $H\cong Z$
, as claimed.
$H\cong Z$
, as claimed.
This brings us to the main result of the current section.
Theorem 5.7.
Let
![]() $F$
be a finitely generated extension of transcendence degree
$F$
be a finitely generated extension of transcendence degree
![]() $r\ge 0$
of a global field
$r\ge 0$
of a global field
![]() $F_0$
of characteristic
$F_0$
of characteristic
![]() $p$
and let
$p$
and let
![]() $F'=F(\mu (F_{0,\mathrm{sep}}))$
. Then,
$F'=F(\mu (F_{0,\mathrm{sep}}))$
. Then,
![]() $\prod _{l\ne p}\mathbb{Z}_l^{r+1}$
is a closed subgroup of
$\prod _{l\ne p}\mathbb{Z}_l^{r+1}$
is a closed subgroup of
![]() $\textrm{Gal}(F')$
, hence also of
$\textrm{Gal}(F')$
, hence also of
![]() $\textrm{Gal}(F)$
.
$\textrm{Gal}(F)$
.
Proof. In the case where
![]() $r=0$
,
$r=0$
,
![]() $F$
itself is a global field, hence Hilbertian [Reference Fried and Jarden3, p. 242, Thm. 13.4.2]. Since
$F$
itself is a global field, hence Hilbertian [Reference Fried and Jarden3, p. 242, Thm. 13.4.2]. Since
![]() $F'$
is an abelian extension of
$F'$
is an abelian extension of
![]() $F$
, a theorem of Kuyk asserts that
$F$
, a theorem of Kuyk asserts that
![]() $F'$
is also Hilbertian [Reference Fried and Jarden3, p. 333, Thm. 16.11.3]. Since
$F'$
is also Hilbertian [Reference Fried and Jarden3, p. 333, Thm. 16.11.3]. Since
![]() $F$
is countable, so is
$F$
is countable, so is
![]() $F'$
. By [Reference Fried and Jarden3, p. 379, Thm. 18.5.6], for almost all
$F'$
. By [Reference Fried and Jarden3, p. 379, Thm. 18.5.6], for almost all
![]() $\sigma \in \textrm{Gal}(F')$
(in the sense of the Haar measure of
$\sigma \in \textrm{Gal}(F')$
(in the sense of the Haar measure of
![]() $\textrm{Gal}(F')$
) the closed subgroup
$\textrm{Gal}(F')$
) the closed subgroup
![]() $\langle \sigma \rangle$
of
$\langle \sigma \rangle$
of
![]() $\textrm{Gal}(F')$
generated by
$\textrm{Gal}(F')$
generated by
![]() $\sigma$
is isomorphic to
$\sigma$
is isomorphic to
![]() $\hat{\mathbb{Z}}$
. Since
$\hat{\mathbb{Z}}$
. Since
![]() $\prod _{l\ne p}\mathbb{Z}_l$
is a closed subgroup of
$\prod _{l\ne p}\mathbb{Z}_l$
is a closed subgroup of
![]() $\prod _l\mathbb{Z}_l$
and
$\prod _l\mathbb{Z}_l$
and
![]() $\prod _l\mathbb{Z}_l\cong{\hat{\mathbb{Z}}}$
[Reference Fried and Jarden3, p. 15, Lemma 1.4.5],
$\prod _l\mathbb{Z}_l\cong{\hat{\mathbb{Z}}}$
[Reference Fried and Jarden3, p. 15, Lemma 1.4.5],
![]() $\prod _{l\ne p}\mathbb{Z}_l$
is a closed subgroup of
$\prod _{l\ne p}\mathbb{Z}_l$
is a closed subgroup of
![]() $\textrm{Gal}(F')$
.
$\textrm{Gal}(F')$
.
Alternatively, by a theorem of Whaples, for each
![]() $l\ne p$
the field
$l\ne p$
the field
![]() $F'$
has a Galois extension
$F'$
has a Galois extension
![]() $F'_l$
with
$F'_l$
with
![]() $\textrm{Gal}(F'_l/F')\cong \mathbb{Z}_l$
[Reference Fried and Jarden3, p. 314, Cor. 16.6.7]. Then,
$\textrm{Gal}(F'_l/F')\cong \mathbb{Z}_l$
[Reference Fried and Jarden3, p. 314, Cor. 16.6.7]. Then,
![]() $F''\;:\!=\;\prod _{l\ne p}F'_l$
is a Galois extension of
$F''\;:\!=\;\prod _{l\ne p}F'_l$
is a Galois extension of
![]() $F'$
with
$F'$
with
![]() $ \textrm{Gal}(F''/F')\cong \prod _{l\ne p}\mathbb{Z}_l$
. Since
$ \textrm{Gal}(F''/F')\cong \prod _{l\ne p}\mathbb{Z}_l$
. Since
![]() $\prod _{l\ne p}\mathbb{Z}_l$
is projective [Reference Fried and Jarden3, p. 507, Cor. 22.4.6], the restriction map
$\prod _{l\ne p}\mathbb{Z}_l$
is projective [Reference Fried and Jarden3, p. 507, Cor. 22.4.6], the restriction map
![]() $\textrm{Gal}(F')\to \textrm{Gal}(F''/F')$
splits [Reference Fried and Jarden3, p. 506, Remark 22.4.2]. Hence, again,
$\textrm{Gal}(F')\to \textrm{Gal}(F''/F')$
splits [Reference Fried and Jarden3, p. 506, Remark 22.4.2]. Hence, again,
![]() $\prod _{l\ne p}\mathbb{Z}_l$
is a closed subgroup of
$\prod _{l\ne p}\mathbb{Z}_l$
is a closed subgroup of
![]() $\textrm{Gal}(F')$
.
$\textrm{Gal}(F')$
.
Next assume by induction that
![]() $r\ge 1$
and the theorem holds for
$r\ge 1$
and the theorem holds for
![]() $r-1$
. Choose a finitely generated extension
$r-1$
. Choose a finitely generated extension
![]() $F_{r-1}$
of transcendence degree
$F_{r-1}$
of transcendence degree
![]() $r-1$
of
$r-1$
of
![]() $F_0$
in
$F_0$
in
![]() $F$
and let
$F$
and let
![]() $F'_{r-1}=F_{r-1}(\mu (F_{0,\mathrm{sep}}))$
. Since
$F'_{r-1}=F_{r-1}(\mu (F_{0,\mathrm{sep}}))$
. Since
![]() $F$
is finitely generated over
$F$
is finitely generated over
![]() $F_0$
of transcendence degree
$F_0$
of transcendence degree
![]() $r$
, we may choose
$r$
, we may choose
![]() $t$
in
$t$
in
![]() $F$
which is transcendental over
$F$
which is transcendental over
![]() $F_{r-1}$
and
$F_{r-1}$
and
![]() $[F\;:\;F_{r-1}(t)]\lt \infty$
. Then,
$[F\;:\;F_{r-1}(t)]\lt \infty$
. Then,
![]() $F'=F'_{r-1}F$
is a finite extension of
$F'=F'_{r-1}F$
is a finite extension of
![]() $F'_{r-1}(t)$
. Let
$F'_{r-1}(t)$
. Let
![]() $L$
be the maximal separable extension of
$L$
be the maximal separable extension of
![]() $F'_{r-1}(t)$
in
$F'_{r-1}(t)$
in
![]() $F'$
, so
$F'$
, so
![]() $F'/L$
is a purely inseparable extension of
$F'/L$
is a purely inseparable extension of
![]() $L$
. Then,
$L$
. Then,
![]() $L$
is a finite separable extension of
$L$
is a finite separable extension of
![]() $F'_{r-1}(t)$
.
$F'_{r-1}(t)$
.

Hence,
By the induction hypothesis,
![]() $\prod _{l\ne p}\mathbb{Z}_l^r$
is a closed subgroup of
$\prod _{l\ne p}\mathbb{Z}_l^r$
is a closed subgroup of
![]() $\textrm{Gal}(F'_{r-1})$
. Therefore, by (5.6), Lemma 5.4, and Lemma 5.6,
$\textrm{Gal}(F'_{r-1})$
. Therefore, by (5.6), Lemma 5.4, and Lemma 5.6,
![]() $\prod _{l\ne p}\mathbb{Z}_l^{r+1}$
is a closed subgroup of
$\prod _{l\ne p}\mathbb{Z}_l^{r+1}$
is a closed subgroup of
![]() $\textrm{Gal}(L)$
. Since
$\textrm{Gal}(L)$
. Since
![]() $F'/L$
is a purely inseparable extension (in particular
$F'/L$
is a purely inseparable extension (in particular
![]() $F'=L$
if
$F'=L$
if
![]() $\mathrm{char}(F_0)=0$
),
$\mathrm{char}(F_0)=0$
),
![]() $\prod _{l\ne p}\mathbb{Z}_l^{r+1}$
is a closed subgroup of
$\prod _{l\ne p}\mathbb{Z}_l^{r+1}$
is a closed subgroup of
![]() $\textrm{Gal}(F')$
, hence also of
$\textrm{Gal}(F')$
, hence also of
![]() $\textrm{Gal}(F)$
, as claimed.
$\textrm{Gal}(F)$
, as claimed.
Remark 5.8.
Let
![]() $F$
be a field as in Theorem
5.7
. If
$F$
be a field as in Theorem
5.7
. If
![]() $p=0$
, then
$p=0$
, then
![]() ${\hat{\mathbb{Z}}}^{r+1}=\prod _{l\ne p}\mathbb{Z}_l^{r+1}$
. Hence, by that theorem,
${\hat{\mathbb{Z}}}^{r+1}=\prod _{l\ne p}\mathbb{Z}_l^{r+1}$
. Hence, by that theorem,
![]() ${\hat{\mathbb{Z}}}^{r+1}$
is isomorphic to a closed subgroup of
${\hat{\mathbb{Z}}}^{r+1}$
is isomorphic to a closed subgroup of
![]() $\textrm{Gal}(F)$
.
$\textrm{Gal}(F)$
.
If
![]() $p\ne 0$
but
$p\ne 0$
but
![]() $r=0$
, then
$r=0$
, then
![]() $F=F_0$
is a countable Hilbertian field and again, by [
Reference Fried and Jarden3, p. 379, Thm. 18.5.6], for almost all
$F=F_0$
is a countable Hilbertian field and again, by [
Reference Fried and Jarden3, p. 379, Thm. 18.5.6], for almost all
![]() $\sigma \in \textrm{Gal}(F)$
we have
$\sigma \in \textrm{Gal}(F)$
we have
![]() $\langle \sigma \rangle \cong{\hat{\mathbb{Z}}}$
.
$\langle \sigma \rangle \cong{\hat{\mathbb{Z}}}$
.
However, by [
Reference Ribes9, p. 256, Thm. 3.3],
![]() $\mathrm{cd}_p(\textrm{Gal}(F))\le 1$
. On the other hand, by [
Reference Ribes9, p. 221, Prop. 4.4],
$\mathrm{cd}_p(\textrm{Gal}(F))\le 1$
. On the other hand, by [
Reference Ribes9, p. 221, Prop. 4.4],
![]() $\mathrm{cd}_p(\mathbb{Z}_p^{r+1})=r+1\ge 2$
if
$\mathrm{cd}_p(\mathbb{Z}_p^{r+1})=r+1\ge 2$
if
![]() $r\ge 1$
. Hence,
$r\ge 1$
. Hence,
![]() $\mathbb{Z}_p^{r+1}$
is isomorphic to no closed subgroup of
$\mathbb{Z}_p^{r+1}$
is isomorphic to no closed subgroup of
![]() $\textrm{Gal}(F)$
. Therefore,
$\textrm{Gal}(F)$
. Therefore,
![]() ${\hat{\mathbb{Z}}}^{r+1}$
is isomorphic to no closed subgroup of
${\hat{\mathbb{Z}}}^{r+1}$
is isomorphic to no closed subgroup of
![]() $\textrm{Gal}(F)$
.
$\textrm{Gal}(F)$
.
Acknowledgement
The author thanks Ido Efrat for many comments on earlier versions of this note. The author also thanks Aharon Razon for a careful reading of the manuscript.