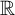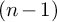1 Introduction
A quasimorphism on a group G is a function f from G to the real numbers
![]() $\mathbb {R}$
such that
$\mathbb {R}$
such that
![]() $\sup _{a,b\in G}|f(ab)-f(a)-f(b)|<\infty $
, where
$\sup _{a,b\in G}|f(ab)-f(a)-f(b)|<\infty $
, where
![]() $\sup _{a,b\in G}|f(ab)-f(a)-f(b)|$
is called the defect of f and is denoted by
$\sup _{a,b\in G}|f(ab)-f(a)-f(b)|$
is called the defect of f and is denoted by
![]() $D_f$
. A function
$D_f$
. A function
![]() $f\colon G\to \mathbb {R}$
is said to be homogeneous if
$f\colon G\to \mathbb {R}$
is said to be homogeneous if
![]() $f(g^k)=kf(g)$
for all
$f(g^k)=kf(g)$
for all
![]() $g\in G$
and integers k. In this article, we focus on the fractional Dehn twist coefficient (FDTC), a certain homogeneous quasimorphism on the braid group on n strands. The FDTC appears in several contexts concerning different aspects of low-dimensional topology; see, for example, Gabai–Oertel, Malyutin and Honda–Kazez–Matić [Reference Gabai and OertelGO89, Reference MalyutinMal04, Reference Honda, Kazez and MatićHKM07, Reference Honda, Kazez and MatićHKM08].
$g\in G$
and integers k. In this article, we focus on the fractional Dehn twist coefficient (FDTC), a certain homogeneous quasimorphism on the braid group on n strands. The FDTC appears in several contexts concerning different aspects of low-dimensional topology; see, for example, Gabai–Oertel, Malyutin and Honda–Kazez–Matić [Reference Gabai and OertelGO89, Reference MalyutinMal04, Reference Honda, Kazez and MatićHKM07, Reference Honda, Kazez and MatićHKM08].
A characterization of the FDTC as the homogeneous quasimorphism of smallest defect
For a fixed integer
![]() $n\geq 1$
, we denote by
$n\geq 1$
, we denote by
Artin’s braid group [Reference ArtinArt25]. For the entire text, we identify
![]() $B_{n-1}\subset B_n$
as a subgroup via the inclusion
$B_{n-1}\subset B_n$
as a subgroup via the inclusion
![]() $\iota \colon B_{n-1}\to B_n,a_i\mapsto a_{i+1}$
whenever
$\iota \colon B_{n-1}\to B_n,a_i\mapsto a_{i+1}$
whenever
![]() $n\geq 2$
. We delay an explicit definition of the FDTC. However, we recall that the FDTC, denoted by
$n\geq 2$
. We delay an explicit definition of the FDTC. However, we recall that the FDTC, denoted by
![]() ${\omega }\colon B_n\to \mathbb {R}$
, is known to be a homogeneous quasimorphism of defect
${\omega }\colon B_n\to \mathbb {R}$
, is known to be a homogeneous quasimorphism of defect
![]() $\leq 1$
(in fact it is know to have defect 1 when
$\leq 1$
(in fact it is know to have defect 1 when
![]() $n\geq 3$
; compare Lemma 10) that satisfies
$n\geq 3$
; compare Lemma 10) that satisfies
![]() ${\omega }(B_{n-1})=\{0\}$
and
${\omega }(B_{n-1})=\{0\}$
and
![]() ${\omega }\left (\Delta ^2\right )=1$
; see [Reference MalyutinMal04]. Here,
${\omega }\left (\Delta ^2\right )=1$
; see [Reference MalyutinMal04]. Here,
![]() $\Delta ^2$
denotes
$\Delta ^2$
denotes
![]() $(a_1a_2\cdots a_{n-1})^n\in B_n$
, which is known as the positive full twist and, for
$(a_1a_2\cdots a_{n-1})^n\in B_n$
, which is known as the positive full twist and, for
![]() $n\geq 3$
, generates the center of
$n\geq 3$
, generates the center of
![]() $B_n$
. We establish that these properties characterize the FDTC.
$B_n$
. We establish that these properties characterize the FDTC.
Theorem 1. For every integer
![]() $n\geq 3$
, there exists a unique homogeneous quasimorphism
$n\geq 3$
, there exists a unique homogeneous quasimorphism
![]() ${\omega }\colon B_n\to \mathbb {R}$
with defect at most 1 that satisfies the following properties:
${\omega }\colon B_n\to \mathbb {R}$
with defect at most 1 that satisfies the following properties:
-
(i)
 ${\omega }\left (\Delta ^2\right )=1$
and
${\omega }\left (\Delta ^2\right )=1$
and -
(ii)
 ${\omega }(\beta )=0$
for all
${\omega }(\beta )=0$
for all
 $\beta \in B_{n-1}\subset B_n$
.
$\beta \in B_{n-1}\subset B_n$
.
We exclude considerations for
![]() $n=2$
(and
$n=2$
(and
![]() $n=1$
) as it is clear that there is at most one homogeneous quasimorphism on the infinite cyclic group
$n=1$
) as it is clear that there is at most one homogeneous quasimorphism on the infinite cyclic group
![]() $B_2$
(and the trivial group
$B_2$
(and the trivial group
![]() $B_1$
) that sends
$B_1$
) that sends
![]() $\Delta ^2$
to a given value since homogeneous quasimorphisms on Abelian groups are group homomorphisms. In contrast to this and to Theorem 1, for
$\Delta ^2$
to a given value since homogeneous quasimorphisms on Abelian groups are group homomorphisms. In contrast to this and to Theorem 1, for
![]() $n\geq 3$
there are many homogeneous quasimorphisms on
$n\geq 3$
there are many homogeneous quasimorphisms on
![]() $B_n$
.
$B_n$
.
Proposition 2. For every integer
![]() $n\geq 3$
and every
$n\geq 3$
and every
![]() $\varepsilon>0$
, there exist continuum-many linearly independent homogeneous quasimorphisms
$\varepsilon>0$
, there exist continuum-many linearly independent homogeneous quasimorphisms
![]() $f\colon B_n\to \mathbb {R}$
with defect at most
$f\colon B_n\to \mathbb {R}$
with defect at most
![]() $1+\varepsilon $
that satisfy (i)
$1+\varepsilon $
that satisfy (i)
![]() $f\left (\Delta ^2\right )=1$
and (ii)
$f\left (\Delta ^2\right )=1$
and (ii)
![]() $f(B_{n-1})=\{0\}$
.
$f(B_{n-1})=\{0\}$
.
We briefly comment on the two assumptions (i) and (ii).
Equation (i) can be understood as a normalization condition. In other words, Theorem 1 says that the homogeneous quasimorphisms
![]() $f\colon B_n\to \mathbb {R}$
that satisfy
$f\colon B_n\to \mathbb {R}$
that satisfy
form a one-dimensional
![]() $\mathbb {R}$
-subspace of the vector space of functions from
$\mathbb {R}$
-subspace of the vector space of functions from
![]() $B_n$
to
$B_n$
to
![]() $\mathbb {R}$
, while Proposition 2 says that the
$\mathbb {R}$
, while Proposition 2 says that the
![]() $\mathbb {R}$
-subspace generated by homogeneous quasimorphisms
$\mathbb {R}$
-subspace generated by homogeneous quasimorphisms
![]() $f\colon B_n\to \mathbb {R}$
that satisfy
$f\colon B_n\to \mathbb {R}$
that satisfy
has uncountably infinite dimension.
Every homogeneous quasimorphism
![]() $f\colon B_n\to \mathbb {R}$
can be written as the sum of a homogeneous quasimorphism that satisfy Equation (ii) and a homogeneous quasimorphism that is determined by the homogeneous quasimorphism
$f\colon B_n\to \mathbb {R}$
can be written as the sum of a homogeneous quasimorphism that satisfy Equation (ii) and a homogeneous quasimorphism that is determined by the homogeneous quasimorphism
![]() ${B_{n-1}}\to \mathbb {R}, \beta \mapsto f(\iota (\beta ))$
[Reference MalyutinMal09, Theorem 2]. So, informally speaking, understanding homogeneous quasimorphisms on
${B_{n-1}}\to \mathbb {R}, \beta \mapsto f(\iota (\beta ))$
[Reference MalyutinMal09, Theorem 2]. So, informally speaking, understanding homogeneous quasimorphisms on
![]() $B_n$
amounts to understanding homogeneous quasimorphisms that satisfy Equation (ii) on
$B_n$
amounts to understanding homogeneous quasimorphisms that satisfy Equation (ii) on
![]() $B_n$
and homogeneous quasimorphisms on
$B_n$
and homogeneous quasimorphisms on
![]() $B_{n-1}$
.
$B_{n-1}$
.
The slice-Bennequin inequality for the FDTC
For a link L – a non-empty oriented closed smooth 1-submanifold of the 3-sphere
![]() $S^3$
– denote by
$S^3$
– denote by
![]() $\chi _4(L)$
the largest integer among the Euler characteristics of smooth oriented surfaces in the
$\chi _4(L)$
the largest integer among the Euler characteristics of smooth oriented surfaces in the
![]() $4$
-ball
$4$
-ball
![]() $B^4$
without closed components and oriented boundary
$B^4$
without closed components and oriented boundary
![]() $L\subset \partial B^4=S^3$
. In particular, for a knot K – a connected link – one has
$L\subset \partial B^4=S^3$
. In particular, for a knot K – a connected link – one has
![]() $2g_4(K)=1-\chi _4(K)$
, where
$2g_4(K)=1-\chi _4(K)$
, where
![]() $g_4$
denotes the slice genus. The slice-Bennequin inequality states that
$g_4$
denotes the slice genus. The slice-Bennequin inequality states that
where
![]() $\mathrm {{wr}}\colon B_n\to \mathbb {Z}$
denotes the writhe, the group homomorphism with
$\mathrm {{wr}}\colon B_n\to \mathbb {Z}$
denotes the writhe, the group homomorphism with
![]() $\mathrm {{wr}}(a_i)=1$
, and
$\mathrm {{wr}}(a_i)=1$
, and
![]() $\widehat {\beta }$
denotes the link obtained as the closure of
$\widehat {\beta }$
denotes the link obtained as the closure of
![]() $\beta $
. For
$\beta $
. For
![]() $\beta $
with closure a knot, Equation (1) reads
$\beta $
with closure a knot, Equation (1) reads
![]() $\left |\mathrm {{wr}}(\beta )\right |\leq 2g_4\left (\widehat {\beta }\right )+n-1$
. As before, we only consider
$\left |\mathrm {{wr}}(\beta )\right |\leq 2g_4\left (\widehat {\beta }\right )+n-1$
. As before, we only consider
![]() $n\geq 3$
as
$n\geq 3$
as
![]() $n\leq 2$
yields no new insight.
$n\leq 2$
yields no new insight.
One may wonder which other maps
![]() $f\colon B_n\to \mathbb {R}$
satisfy a similar inequality. Concretely, [Reference Hubbard, Kawamuro, Kose, Martin, Plamenevskaya, Raoux, Truong and TurnerHKK+21, Question 1.6] asks whether, for each
$f\colon B_n\to \mathbb {R}$
satisfy a similar inequality. Concretely, [Reference Hubbard, Kawamuro, Kose, Martin, Plamenevskaya, Raoux, Truong and TurnerHKK+21, Question 1.6] asks whether, for each
![]() $n\geq 3$
, there exist constants
$n\geq 3$
, there exist constants
![]() $A(n)$
and
$A(n)$
and
![]() $C(n)$
such that
$C(n)$
such that
![]() ${\omega }(\beta )\leq A(n)g_4\left (\widehat {\beta }\right )+C(n)$
for all
${\omega }(\beta )\leq A(n)g_4\left (\widehat {\beta }\right )+C(n)$
for all
![]() $\beta \in B_n$
with closure a knot. We answer affirmatively with
$\beta \in B_n$
with closure a knot. We answer affirmatively with
![]() $A(n)$
independent of n; concretely,
$A(n)$
independent of n; concretely,
![]() $A(n)=2$
, which is optimal (e.g., by the examples from [Reference Hubbard, Kawamuro, Kose, Martin, Plamenevskaya, Raoux, Truong and TurnerHKK+21, Prop. 4.7]).
$A(n)=2$
, which is optimal (e.g., by the examples from [Reference Hubbard, Kawamuro, Kose, Martin, Plamenevskaya, Raoux, Truong and TurnerHKK+21, Prop. 4.7]).
Theorem 3. For all integers
![]() $n\geq 3$
, we have that the FDTC
$n\geq 3$
, we have that the FDTC
![]() ${\omega }\colon B_n\to \mathbb {R}$
satisfies
${\omega }\colon B_n\to \mathbb {R}$
satisfies
Theorem 3 provides the affirmative answer claimed above since it reads
![]() $|{\omega }(\beta )|\leq 2g_4\left (\widehat {\beta }\right )+n-1$
for all
$|{\omega }(\beta )|\leq 2g_4\left (\widehat {\beta }\right )+n-1$
for all
![]() $\beta \in B_n$
such that
$\beta \in B_n$
such that
![]() $\widehat {\beta }$
is a knot.
$\widehat {\beta }$
is a knot.
We provide more context for Theorem 3 in Section 2. The main input in the proof of Theorem 3 is that the FDTC can be expressed in terms of the so-called homogenization of an instance of upsilon. Here, upsilon is a knot invariant, introduced in [Reference Ozsváth, Stipsicz and SzabóOSS17], that has being a lower bound for the slice genus as a key feature; see Section 5.
Comparing bounds on the defect and affine linear bounds for the slice genus
At this point, the reader may have wondered why Theorem 1 and Theorem 3 appear in the same text, given they are concerned with different aspects of the FDTC. A link between these aspects is provided in Proposition 5 below.
We ask whether satisfying the slice-Bennequin inequality as described in Theorem 3 characterizes the FDTC in the same way that having defect 1 does characterize the FDTC by Theorem 1.
Question 4. Fix an integer
![]() $n\geq 3$
. Is the FDTC the unique homogeneous quasimorphism
$n\geq 3$
. Is the FDTC the unique homogeneous quasimorphism
![]() ${\omega }\colon B_n\to \mathbb {R}$
that satisfies
${\omega }\colon B_n\to \mathbb {R}$
that satisfies
![]() ${\omega }\left (\Delta ^2\right )=1$
,
${\omega }\left (\Delta ^2\right )=1$
,
![]() ${\omega }(\beta )=0$
for all
${\omega }(\beta )=0$
for all
![]() $\beta \in B_{n-1}\subset B_n$
and for which there exists a constant C such that
$\beta \in B_{n-1}\subset B_n$
and for which there exists a constant C such that
While we are unable to answer this question, we provide the following connection between the defect of a quasimorphism f and the possible slopes of affine linear bounds for
![]() $g_4\left (\widehat {\beta }\right )$
in terms of
$g_4\left (\widehat {\beta }\right )$
in terms of
![]() $f(\beta )$
.
$f(\beta )$
.
Proposition 5. Fix
![]() $n\geq 3$
, and let
$n\geq 3$
, and let
![]() $f\colon B_n\to \mathbb {R}$
be a homogeneous quasimorphism. If there exist constants
$f\colon B_n\to \mathbb {R}$
be a homogeneous quasimorphism. If there exist constants
![]() $A,C\in \mathbb {R}$
such that
$A,C\in \mathbb {R}$
such that
then the defect
![]() $D_f$
of f satisfies
$D_f$
of f satisfies
![]() $D_f\leq \frac {A}{2}(n-1)$
.
$D_f\leq \frac {A}{2}(n-1)$
.
In a first version of this article, the conclusion of Proposition 5 stated
![]() $D_f\leq A(n-1) $
. The factor
$D_f\leq A(n-1) $
. The factor
![]() $1/2$
improvement was pointed out by Tetsuya Ito.
$1/2$
improvement was pointed out by Tetsuya Ito.
Proposition 5 can be understood as a first step towards affirmatively answering Question 4. Concretely, we have the following corollary.
Corollary 6. Fix
![]() $n\geq 3$
, and let
$n\geq 3$
, and let
![]() $f\colon B_n\to \mathbb {R}$
be a homogeneous quasimorphism. that satisfies
$f\colon B_n\to \mathbb {R}$
be a homogeneous quasimorphism. that satisfies
![]() $f\left (B_{n-1}\right )=\{0\}$
and
$f\left (B_{n-1}\right )=\{0\}$
and
![]() $f(\Delta ^2)=1$
. If there exist constants
$f(\Delta ^2)=1$
. If there exist constants
![]() $A,C\in \mathbb {R}$
such that
$A,C\in \mathbb {R}$
such that
![]() $\left |f(\beta )\right |\leq Ag_4\left (\widehat {\beta }\right )+C\text { for all } \beta \in B_n \text { with closure a knot}, $
then
$\left |f(\beta )\right |\leq Ag_4\left (\widehat {\beta }\right )+C\text { for all } \beta \in B_n \text { with closure a knot}, $
then
![]() $A>\frac {2}{n-1}$
.
$A>\frac {2}{n-1}$
.
Proof of Corollary 6.
Assume towards a contradiction that
![]() $A\leq \frac {2}{n-1}$
. Then
$A\leq \frac {2}{n-1}$
. Then
![]() $D_f\leq \frac {A}{2}(n-1)\leq 1$
by Proposition 5, hence
$D_f\leq \frac {A}{2}(n-1)\leq 1$
by Proposition 5, hence
![]() $f={\omega }$
by Theorem 1. However, for
$f={\omega }$
by Theorem 1. However, for
![]() $f={\omega }$
, we have
$f={\omega }$
, we have
![]() $A\geq 2$
, for example, by the examples from [Reference Hubbard, Kawamuro, Kose, Martin, Plamenevskaya, Raoux, Truong and TurnerHKK+21, Prop. 4.7].
$A\geq 2$
, for example, by the examples from [Reference Hubbard, Kawamuro, Kose, Martin, Plamenevskaya, Raoux, Truong and TurnerHKK+21, Prop. 4.7].
We do not expect Proposition 5 to be optimal. If the inequality for
![]() $D_f$
in Proposition 5 can be strengthened, concretely, if the next question can be answered affirmatively, then Theorem 1 implies that Question 4 can be answered affirmatively (by arguing as in the proof of Corollary 6).
$D_f$
in Proposition 5 can be strengthened, concretely, if the next question can be answered affirmatively, then Theorem 1 implies that Question 4 can be answered affirmatively (by arguing as in the proof of Corollary 6).
Question 7. Fix
![]() $n\geq 3$
, and let
$n\geq 3$
, and let
![]() $f\colon B_n\to \mathbb {R}$
be a homogeneous quasimorphism that satisfies
$f\colon B_n\to \mathbb {R}$
be a homogeneous quasimorphism that satisfies
![]() $f\left (B_{n-1}\right )=\{0\}$
. If there exist constants
$f\left (B_{n-1}\right )=\{0\}$
. If there exist constants
![]() $A,C\in \mathbb {R}$
such that
$A,C\in \mathbb {R}$
such that
does the defect
![]() $D_f$
of f satisfy
$D_f$
of f satisfy
![]() $D_f\leq A/2$
?
$D_f\leq A/2$
?
Ingredients for the proofs and structure of the paper
In Section 2, we provide context for Theorem 3.
In Section 3, we establish Theorem 1. The main step in the proof of Theorem 1 is to show that every braid
![]() $\beta \in B_n$
that can be written as a braid word that contains at most l occurrences of
$\beta \in B_n$
that can be written as a braid word that contains at most l occurrences of
![]() $a_1$
and no
$a_1$
and no
![]() $a_1^{-1}$
can be decomposed as a particular product of full twists
$a_1^{-1}$
can be decomposed as a particular product of full twists
![]() $\Delta ^2$
and at most l braids that are conjugate to braids in
$\Delta ^2$
and at most l braids that are conjugate to braids in
![]() $B_{n-1}\subset B_n$
.
$B_{n-1}\subset B_n$
.
In Section 4, we show that Proposition 2 is a rather immediate consequence of the work on group actions on
![]() $\delta $
-hyperbolic spaces that satisfy weak proper discontinuity (WPD) [Reference Bestvina and FujiwaraBF02].
$\delta $
-hyperbolic spaces that satisfy weak proper discontinuity (WPD) [Reference Bestvina and FujiwaraBF02].
In Section 5, we establish Theorem 3. A key ingredient is the reinterpretation of the FDTC as a linear combination of the writhe and the homogenization of
![]() $\Upsilon (t)$
[Reference Feller and HubbardFH19, Theorem 1.3]. Additionally, we use some facts about concordances between braid closures. The latter is also what we use in the proof of Proposition 5.
$\Upsilon (t)$
[Reference Feller and HubbardFH19, Theorem 1.3]. Additionally, we use some facts about concordances between braid closures. The latter is also what we use in the proof of Proposition 5.
We conclude the paper with a perspective that allows to view both the slice-Bennequin (1) and Theorem 3 as instances of an observation concerning the homogenization of
![]() $1$
-Lipschitz concordance homomorphisms; see Appendix A.
$1$
-Lipschitz concordance homomorphisms; see Appendix A.
2 Context for Theorem 3: Bennequin and slice-Bennequin inequalities
For simplicity of exposition, in this section all braids
![]() $\beta $
are assumed to have a knot as their closure. All that is said translates to the general setup if
$\beta $
are assumed to have a knot as their closure. All that is said translates to the general setup if
![]() $g_k$
is replaced by
$g_k$
is replaced by
![]() $-(\chi _k-1)/2$
for
$-(\chi _k-1)/2$
for
![]() $k\in \{3,4\}$
.
$k\in \{3,4\}$
.
The Bennequin inequality
The slice-Bennequin inequality
was predated by the Bennequin inequality
where
![]() $g_3$
denotes the smallest genus among smooth surface in
$g_3$
denotes the smallest genus among smooth surface in
![]() $S^3$
with boundary the knot.
$S^3$
with boundary the knot.
There is a conceptual gap between these two results. The slice-Bennequin inequality needed a strong input from smooth
![]() $4$
-manifold theory: the so-called local-Thom conjecture as proven by Kronheimer and Mrowka [Reference Kronheimer and MrowkaKM93, Corollary 1.3]. The ‘smooth’ is crucial here. Indeed, the analog statement in the locally flat setting (where
$4$
-manifold theory: the so-called local-Thom conjecture as proven by Kronheimer and Mrowka [Reference Kronheimer and MrowkaKM93, Corollary 1.3]. The ‘smooth’ is crucial here. Indeed, the analog statement in the locally flat setting (where
![]() $g_4$
is replaced with the topological slice genus) is well known to fail in many instances; see, for example, [Reference RudolphRud93, Reference RudolphRud84, Reference Baader, Feller, Lewark and LiechtiBFLL18].
$g_4$
is replaced with the topological slice genus) is well known to fail in many instances; see, for example, [Reference RudolphRud93, Reference RudolphRud84, Reference Baader, Feller, Lewark and LiechtiBFLL18].
Concerning the FDTC, we point to a version of the Bennequin inequality by Ito [Reference ItoIto11, Theorem 1.2]:
![]() ${\omega }(\beta )< 2g_3\left (\widehat {\beta }\right )\frac {2}{n+2}-\frac {2}{n+2}+\frac {3}{2}$
for all
${\omega }(\beta )< 2g_3\left (\widehat {\beta }\right )\frac {2}{n+2}-\frac {2}{n+2}+\frac {3}{2}$
for all
![]() $\beta \in B_n$
.Footnote
1
Meaning that the Bennequin inequality holds with a slope
$\beta \in B_n$
.Footnote
1
Meaning that the Bennequin inequality holds with a slope
![]() $A(n)$
for which it is known not to hold when
$A(n)$
for which it is known not to hold when
![]() $g_3$
is replaced by
$g_3$
is replaced by
![]() $g_4$
.
$g_4$
.
The slice-Bennequin inequality for (quasi-)positive braids
Recall that the key input for Rudolph’s proof of the slice-Bennequin inequality (1) is that it holds (in fact with equality) for positive braids with closure a torus knot (by the local Thom conjecture [Reference Kronheimer and MrowkaKM93, Corollary 1.3]) and hence, as observed by Rudolph, also for positive (actually also quasipositive) braids. Then Equation (1) follows using that, for all
![]() $\beta \in B_n$
and generators
$\beta \in B_n$
and generators
![]() $a_i$
,
$a_i$
,
![]() $\mathrm {{wr}}(\beta a_i)-\mathrm {{wr}}(\beta )\geq 1$
and there exists a cobordism with Euler characteristic
$\mathrm {{wr}}(\beta a_i)-\mathrm {{wr}}(\beta )\geq 1$
and there exists a cobordism with Euler characteristic
![]() $-1$
between the closures of
$-1$
between the closures of
![]() $\beta a_i$
and
$\beta a_i$
and
![]() $\beta $
. For the FDTC, combining
$\beta $
. For the FDTC, combining
![]() ${\omega }(\beta )\leq \mathrm {{wr}}(\beta )-1$
for quasipositive braids
${\omega }(\beta )\leq \mathrm {{wr}}(\beta )-1$
for quasipositive braids
![]() $\beta \neq 1$
(this follows readily by using that
$\beta \neq 1$
(this follows readily by using that
![]() $\omega (a_i)=0$
, which is implied by
$\omega (a_i)=0$
, which is implied by
![]() ${\omega }(B_{n-1})=\{0\}$
, and that
${\omega }(B_{n-1})=\{0\}$
, and that
![]() ${\omega }$
is homogeneous quasimorphism of defect at most 1) with Equation (1) yields
${\omega }$
is homogeneous quasimorphism of defect at most 1) with Equation (1) yields
see [Reference Hubbard, Kawamuro, Kose, Martin, Plamenevskaya, Raoux, Truong and TurnerHKK+21, Theorem 1.5]. However, the strategy of reducing to the statement for positive (or quasipositive) braids cannot be carried over to establish the slice-Bennequin inequality for the FDTC since
![]() ${\omega }(\beta a_i)-{\omega }(\beta )\geq 1$
does not hold in general. Also, there is no bound on
${\omega }(\beta a_i)-{\omega }(\beta )\geq 1$
does not hold in general. Also, there is no bound on
![]() ${\omega }(\beta )$
in terms of an expression depending on
${\omega }(\beta )$
in terms of an expression depending on
![]() $\mathrm {{wr}}(\beta )$
that holds for all braids
$\mathrm {{wr}}(\beta )$
that holds for all braids
![]() $\beta \in B_n$
.
$\beta \in B_n$
.
Does a version of the slice-Bennequin inequality hold for all quasimorphisms?
In light of the writhe and FDTC satisfying the slice-Bennequin inequality, one might wonder whether, for each braid group
![]() $B_n$
with
$B_n$
with
![]() $n\geq 3$
, there exists a quasimorphism
$n\geq 3$
, there exists a quasimorphism
![]() $f\colon B_n\to \mathbb {R}$
which does not satisfy a version of the slice-Bennequin inequality. We state this precisely.
$f\colon B_n\to \mathbb {R}$
which does not satisfy a version of the slice-Bennequin inequality. We state this precisely.
Question 8. Fix
![]() $n\geq 3$
. Does there exist a quasimorphism
$n\geq 3$
. Does there exist a quasimorphism
![]() $f\colon B_n\to \mathbb {R}$
such that, for every
$f\colon B_n\to \mathbb {R}$
such that, for every
![]() $A,C\in \mathbb {R}$
, there exists a
$A,C\in \mathbb {R}$
, there exists a
![]() $\beta \in B_n$
with closure a knot such that
$\beta \in B_n$
with closure a knot such that
![]() $|f(\beta )|>Ag_4\left (\widehat {\beta }\right )+C$
?
$|f(\beta )|>Ag_4\left (\widehat {\beta }\right )+C$
?
We note that, since every quasimorphism is at bounded distance of a homogeneous one, asking the question for homogeneous quasimorphisms or quasimorphisms amounts to the same.
We suspect that many (if not most) quasimorphisms do not satisfy a version of the slice-Bennequin inequality; why, after all, would there be such a connection between quasimorphisms and concordance? For example, we suspect that many Brooks-like quasimorphisms as provided in [Reference Bestvina and FujiwaraBF02] (a construction that, as far as we know, is devoid of connections to concordance) are quasimorphisms as asked for in Question 8. However, we are not able to confirm this at this point.
To answer Question 8 in the positive, the reader might be tempted (the author certainly was) to construct a homogeneous quasimorphism
![]() $f\colon B_n\to \mathbb {R}$
that is nonzero on some braid
$f\colon B_n\to \mathbb {R}$
that is nonzero on some braid
![]() $\beta $
with the property that
$\beta $
with the property that
![]() $\lim _{k\to \infty } \frac {\chi _4\left (\widehat {\beta ^k}\right )}{k}=0$
. Indeed, one readily checks that such an f is as asked for in Question 8. However, the only braids we are able to find with the property
$\lim _{k\to \infty } \frac {\chi _4\left (\widehat {\beta ^k}\right )}{k}=0$
. Indeed, one readily checks that such an f is as asked for in Question 8. However, the only braids we are able to find with the property
![]() $\lim _{k\to \infty } \frac {\chi _4\left (\widehat {\beta ^k}\right )}{k}=0$
are braids that are (up to taking conjugates) of the form
$\lim _{k\to \infty } \frac {\chi _4\left (\widehat {\beta ^k}\right )}{k}=0$
are braids that are (up to taking conjugates) of the form
![]() $\alpha \overline {\alpha ^{-1}}$
for some braid
$\alpha \overline {\alpha ^{-1}}$
for some braid
![]() $\alpha $
, and a small calculation reveals that, for all
$\alpha $
, and a small calculation reveals that, for all
![]() $\alpha \in B_n$
, all homogeneous quasimorphisms
$\alpha \in B_n$
, all homogeneous quasimorphisms
![]() $f\colon B_n\to \mathbb {R}$
vanish on
$f\colon B_n\to \mathbb {R}$
vanish on
![]() $\alpha \overline {\alpha ^{-1}}$
. (Here,
$\alpha \overline {\alpha ^{-1}}$
. (Here,
![]() $\overline {\gamma }\in B_n$
is the result of changing all
$\overline {\gamma }\in B_n$
is the result of changing all
![]() $a_i^{\pm 1}$
in a braid word for
$a_i^{\pm 1}$
in a braid word for
![]() $\gamma \in B_n$
to
$\gamma \in B_n$
to
![]() $a_{n-i}^{\pm 1}$
.)
$a_{n-i}^{\pm 1}$
.)
3 The proof of Theorem 1
Definition of the FDTC via the Dehornoy order
We fix an integer
![]() $n\geq 2$
. A braid
$n\geq 2$
. A braid
![]() $\beta $
is said to be Dehornoy positive, denoted by
$\beta $
is said to be Dehornoy positive, denoted by
![]() $\beta \succ _{\textrm {Deh}} 1$
, if it can be written as a braid word that, for some integer
$\beta \succ _{\textrm {Deh}} 1$
, if it can be written as a braid word that, for some integer
![]() $1\leq i<n$
, contains a braid generator
$1\leq i<n$
, contains a braid generator
![]() $a_i$
but no
$a_i$
but no
![]() $a_i^{-1}$
or any generators
$a_i^{-1}$
or any generators
![]() $a_j^{\pm 1}$
for
$a_j^{\pm 1}$
for
![]() $j<i$
. We write
$j<i$
. We write
![]() $\beta \succeq _{\textrm {Deh}} 1$
if
$\beta \succeq _{\textrm {Deh}} 1$
if
![]() $\beta \succ _{\textrm {Deh}} 1$
or
$\beta \succ _{\textrm {Deh}} 1$
or
![]() $\beta =1$
. Dehornoy showed that this gives a well-defined left-invariant total order
$\beta =1$
. Dehornoy showed that this gives a well-defined left-invariant total order
![]() $\succeq _{\textrm {Deh}}$
on
$\succeq _{\textrm {Deh}}$
on
![]() $B_n$
by setting
$B_n$
by setting
![]() $\beta \succeq _{\textrm {Deh}}\alpha $
to mean
$\beta \succeq _{\textrm {Deh}}\alpha $
to mean
![]() $\alpha ^{-1}\beta \succeq _{\textrm {Deh}}1$
[Reference DehornoyDeh94]. The Dehornoy floor
$\alpha ^{-1}\beta \succeq _{\textrm {Deh}}1$
[Reference DehornoyDeh94]. The Dehornoy floor
![]() $\lfloor \beta \rfloor $
is the unique integer m such that
$\lfloor \beta \rfloor $
is the unique integer m such that
![]() $(\Delta ^2)^{m+1}\succ _{\textrm {Deh}}\beta \succeq _{\textrm {Deh}}(\Delta ^2)^{m}$
. For any
$(\Delta ^2)^{m+1}\succ _{\textrm {Deh}}\beta \succeq _{\textrm {Deh}}(\Delta ^2)^{m}$
. For any
![]() $\beta \in B_n$
, its fractional Dehn twist coefficient is
$\beta \in B_n$
, its fractional Dehn twist coefficient is ![]() ; see [Reference MalyutinMal04]. In other words,
; see [Reference MalyutinMal04]. In other words,
![]() ${\omega }$
equals the homogenization of the Dehornoy floor. We refer to [Reference MalyutinMal04] for more details on this approach to the FDTC and how one derives its properties (e.g., being a homogeneous quasimorphism with defect at most 1).
${\omega }$
equals the homogenization of the Dehornoy floor. We refer to [Reference MalyutinMal04] for more details on this approach to the FDTC and how one derives its properties (e.g., being a homogeneous quasimorphism with defect at most 1).
Remark 9. It is essentially immediate from this definition that, if
![]() ${\omega }(\beta )>0$
, then
${\omega }(\beta )>0$
, then
![]() $\beta $
can be written as a braid word with at least one
$\beta $
can be written as a braid word with at least one
![]() $a_1$
and no
$a_1$
and no
![]() $a_1^{-1}$
(and, in particular,
$a_1^{-1}$
(and, in particular,
![]() $\beta \succ 1$
). Indeed, if
$\beta \succ 1$
). Indeed, if
![]() $\beta $
can be written as a braid word without
$\beta $
can be written as a braid word without
![]() $a_1$
or
$a_1$
or
![]() $a_1^{-1}$
, then
$a_1^{-1}$
, then
![]() $(\Delta ^2)\succ _{\textrm {Deh}}\beta \succ _{\textrm {Deh}}(\Delta ^2)^{-1}$
. Hence,
$(\Delta ^2)\succ _{\textrm {Deh}}\beta \succ _{\textrm {Deh}}(\Delta ^2)^{-1}$
. Hence,
![]() $1\geq \lfloor \beta ^k\rfloor \geq -1$
, which implies
$1\geq \lfloor \beta ^k\rfloor \geq -1$
, which implies
![]() ${\omega }(\beta )=0$
. Therefore,
${\omega }(\beta )=0$
. Therefore,
![]() $\beta $
can be written as braid word that either contains only
$\beta $
can be written as braid word that either contains only
![]() $a_1$
or only
$a_1$
or only
![]() $a_1^{-1}$
. If it were the latter, then
$a_1^{-1}$
. If it were the latter, then
![]() $1\succ _{\textrm {Deh}}\beta ^k$
, hence
$1\succ _{\textrm {Deh}}\beta ^k$
, hence
![]() $0\geq \lfloor \beta ^k\rfloor $
, which implies
$0\geq \lfloor \beta ^k\rfloor $
, which implies
![]() $0\geq {\omega }(\beta )$
.
$0\geq {\omega }(\beta )$
.
Proof of Theorem 1
The proof below uses relations in the braid group, general properties of homogeneous quasimorphisms and the property of the FDTC discussed in Remark 9.
Proof of Theorem 1.
We fix
![]() $n\geq 3$
and let
$n\geq 3$
and let
![]() ${\omega _*}\colon B_n\to \mathbb {R}$
be any homogeneous quasimorphism that satisfies the assumptions.
${\omega _*}\colon B_n\to \mathbb {R}$
be any homogeneous quasimorphism that satisfies the assumptions.
Assume towards a contradiction that
![]() ${\omega _*}\neq {\omega }$
. Pick
${\omega _*}\neq {\omega }$
. Pick
![]() $\beta _{\textrm {w}}\in B_n$
with
$\beta _{\textrm {w}}\in B_n$
with
![]() ${\omega }(\beta_{\mathrm{w}})-{\omega _*}(\beta_{\mathrm{w}})\neq 0$
. Since
${\omega }(\beta_{\mathrm{w}})-{\omega _*}(\beta_{\mathrm{w}})\neq 0$
. Since
![]() ${\omega _*}$
and
${\omega _*}$
and
![]() ${\omega }$
are homogeneous, there exists
${\omega }$
are homogeneous, there exists
![]() $k_1\in \mathbb {Z}$
such that
$k_1\in \mathbb {Z}$
such that
Since
![]() $f(ab)=f(a)+f(b)$
for all homogeneous quasimorphisms
$f(ab)=f(a)+f(b)$
for all homogeneous quasimorphisms
![]() $f\colon G\to \mathbb {R}$
and commuting
$f\colon G\to \mathbb {R}$
and commuting
![]() $a,b\in G$
, and since
$a,b\in G$
, and since
![]() ${\omega }\left (\Delta ^2\right )={\omega _*}\left (\Delta ^2\right )=1$
, there exists
${\omega }\left (\Delta ^2\right )={\omega _*}\left (\Delta ^2\right )=1$
, there exists
![]() $k_2\in \mathbb {Z}$
such that
$k_2\in \mathbb {Z}$
such that
We define ![]() . Since
. Since
![]() ${\omega }(\beta )>0$
, we have that
${\omega }(\beta )>0$
, we have that
![]() $\beta $
can be given by a braid word with no occurrences of
$\beta $
can be given by a braid word with no occurrences of
![]() $a_1^{-1}$
but at least one
$a_1^{-1}$
but at least one
![]() $a_1$
by Remark 9.
$a_1$
by Remark 9.
We proceed by showing
![]() ${\omega _*}(\beta )\geq 0$
, which contradicts
${\omega _*}(\beta )\geq 0$
, which contradicts
![]() ${\omega _*}(\beta )<0$
. We may and do assume that the number of occurrences of
${\omega _*}(\beta )<0$
. We may and do assume that the number of occurrences of
![]() $a_1$
in the braid word without
$a_1$
in the braid word without
![]() $a_1^{-1}$
we picked for
$a_1^{-1}$
we picked for
![]() $\beta $
is even. (Indeed, otherwise we consider
$\beta $
is even. (Indeed, otherwise we consider
![]() $\beta \beta $
, which also satisfies
$\beta \beta $
, which also satisfies
![]() $0>{\omega _*}(\beta \beta )$
since
$0>{\omega _*}(\beta \beta )$
since
![]() ${\omega _*}(\beta \beta )={\omega _*}(\beta )+{\omega _*}(\beta )$
.) Hence, we have that
${\omega _*}(\beta \beta )={\omega _*}(\beta )+{\omega _*}(\beta )$
.) Hence, we have that
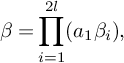 $$\begin{align*}\beta=\prod_{i=1}^{2l}(a_1\beta_i),\end{align*}$$
$$\begin{align*}\beta=\prod_{i=1}^{2l}(a_1\beta_i),\end{align*}$$
where l is a positive integer and the
![]() $\beta _i$
are (possibly trivial) n-braids in
$\beta _i$
are (possibly trivial) n-braids in
![]() $B_{n-1}\subset B_n$
.
$B_{n-1}\subset B_n$
.
Next, we observe that
![]() $\beta $
maybe conjugated to a braid of the form
$\beta $
maybe conjugated to a braid of the form
![]() $\Delta ^{2l}\prod _{i=1}^{l}L_{i}R_{i}$
, where
$\Delta ^{2l}\prod _{i=1}^{l}L_{i}R_{i}$
, where
![]() $R_i$
is an n-braid given by a braid word without
$R_i$
is an n-braid given by a braid word without
![]() $a_1^{\pm 1}$
(in other words an element of
$a_1^{\pm 1}$
(in other words an element of
![]() $B_{n-1}\subset B_n$
) and
$B_{n-1}\subset B_n$
) and
![]() $L_i$
an n-braid given by a braid word without
$L_i$
an n-braid given by a braid word without
![]() $a_{n-1}^{\pm 1}$
. To describe
$a_{n-1}^{\pm 1}$
. To describe
![]() $L_i$
and
$L_i$
and
![]() $R_i$
, we consider the element
$R_i$
, we consider the element
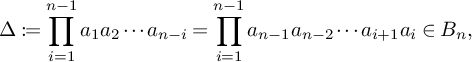
known as the (positive) half-twist since
![]() $\Delta \Delta =\Delta ^2$
. We denote by
$\Delta \Delta =\Delta ^2$
. We denote by
![]() $\Delta _L\in B_n$
and
$\Delta _L\in B_n$
and
![]() $\Delta _R\in B_n$
the half-twist on the first
$\Delta _R\in B_n$
the half-twist on the first
![]() $n-1$
strands and the last
$n-1$
strands and the last
![]() $n-1$
strands, respectively. In other words,
$n-1$
strands, respectively. In other words,
![]() $\Delta _R$
is the image of the half twist
$\Delta _R$
is the image of the half twist
![]() $\Delta \in B_{n-1}$
under the inclusion
$\Delta \in B_{n-1}$
under the inclusion
![]() $\iota \colon B_{n-1}\to B_n,a_i\mapsto a_{i+1}$
, while
$\iota \colon B_{n-1}\to B_n,a_i\mapsto a_{i+1}$
, while
![]() $\Delta _L$
is the image of the half twist
$\Delta _L$
is the image of the half twist
![]() $\Delta \in B_{n-1}$
under the inclusion
$\Delta \in B_{n-1}$
under the inclusion
![]() $a_i\mapsto a_i$
. We also denote by
$a_i\mapsto a_i$
. We also denote by
![]() $\overline {\beta }$
the braid obtained from
$\overline {\beta }$
the braid obtained from
![]() $\beta $
by replacing
$\beta $
by replacing
![]() $a_i^{\pm 1}$
with
$a_i^{\pm 1}$
with
![]() $a_{n-i}^{\pm 1}$
and recall that
$a_{n-i}^{\pm 1}$
and recall that
![]() $\Delta ^{\pm 1}\beta =\overline {\beta }\Delta ^{\pm 1}$
. With this we see
$\Delta ^{\pm 1}\beta =\overline {\beta }\Delta ^{\pm 1}$
. With this we see
 $$ \begin{align*} a_1\beta_{2i-1}a_1\beta_{2i}&=\Delta^2\Delta^{-2}a_1\beta_{2i-1}a_1\beta_{2i}\\ &=\Delta^2\underbrace{\Delta^{-1}}_{\hspace{-2cm}\Delta_R^{-1}\left(a_1^{-1}a_2^{-1}\cdots a_{n-2}^{-1}a_{n-1}^{-1}\right)\hspace{-2cm}} a_{n-1}\overline{\beta_{2i-1}}\overbrace{\Delta^{-1}}^{\hspace{-2cm}\Delta_L^{-1}\left(a_{n-1}^{-1}a_{n-2}^{-1}\cdots a_{2}^{-1}a_1^{-1}\right)\hspace{-2cm}}a_1\beta_{2i}\\ &=\Delta^2\Delta_R^{-1}\left(a_1^{-1}a_2^{-1}\cdots a_{n-2}^{-1}\right)\overline{\beta_{2i-1}}\Delta_L^{-1}\left(a_{n-1}^{-1}a_{n-2}^{-1}\cdots a_{2}^{-1}\right)\beta_{2i}. \end{align*} $$
$$ \begin{align*} a_1\beta_{2i-1}a_1\beta_{2i}&=\Delta^2\Delta^{-2}a_1\beta_{2i-1}a_1\beta_{2i}\\ &=\Delta^2\underbrace{\Delta^{-1}}_{\hspace{-2cm}\Delta_R^{-1}\left(a_1^{-1}a_2^{-1}\cdots a_{n-2}^{-1}a_{n-1}^{-1}\right)\hspace{-2cm}} a_{n-1}\overline{\beta_{2i-1}}\overbrace{\Delta^{-1}}^{\hspace{-2cm}\Delta_L^{-1}\left(a_{n-1}^{-1}a_{n-2}^{-1}\cdots a_{2}^{-1}a_1^{-1}\right)\hspace{-2cm}}a_1\beta_{2i}\\ &=\Delta^2\Delta_R^{-1}\left(a_1^{-1}a_2^{-1}\cdots a_{n-2}^{-1}\right)\overline{\beta_{2i-1}}\Delta_L^{-1}\left(a_{n-1}^{-1}a_{n-2}^{-1}\cdots a_{2}^{-1}\right)\beta_{2i}. \end{align*} $$
Hence,
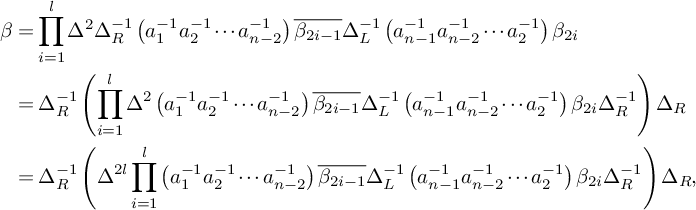 $$ \begin{align*} \beta&=\prod_{i=1}^{l}\Delta^2\Delta_R^{-1}\left(a_1^{-1}a_2^{-1}\cdots a_{n-2}^{-1}\right)\overline{\beta_{2i-1}}\Delta_L^{-1}\left(a_{n-1}^{-1}a_{n-2}^{-1}\cdots a_{2}^{-1}\right)\beta_{2i}\\ &=\Delta_R^{-1}\left(\prod_{i=1}^{l}\Delta^2\left(a_1^{-1}a_2^{-1}\cdots a_{n-2}^{-1}\right)\overline{\beta_{2i-1}}\Delta_L^{-1}\left(a_{n-1}^{-1}a_{n-2}^{-1}\cdots a_{2}^{-1}\right)\beta_{2i}\Delta_R^{-1}\right)\Delta_R\\ &=\Delta_R^{-1}\left(\Delta^{2l}\prod_{i=1}^{l}\left(a_1^{-1}a_2^{-1}\cdots a_{n-2}^{-1}\right)\overline{\beta_{2i-1}}\Delta_L^{-1}\left(a_{n-1}^{-1}a_{n-2}^{-1}\cdots a_{2}^{-1}\right)\beta_{2i}\Delta_R^{-1}\right)\Delta_R, \end{align*} $$
$$ \begin{align*} \beta&=\prod_{i=1}^{l}\Delta^2\Delta_R^{-1}\left(a_1^{-1}a_2^{-1}\cdots a_{n-2}^{-1}\right)\overline{\beta_{2i-1}}\Delta_L^{-1}\left(a_{n-1}^{-1}a_{n-2}^{-1}\cdots a_{2}^{-1}\right)\beta_{2i}\\ &=\Delta_R^{-1}\left(\prod_{i=1}^{l}\Delta^2\left(a_1^{-1}a_2^{-1}\cdots a_{n-2}^{-1}\right)\overline{\beta_{2i-1}}\Delta_L^{-1}\left(a_{n-1}^{-1}a_{n-2}^{-1}\cdots a_{2}^{-1}\right)\beta_{2i}\Delta_R^{-1}\right)\Delta_R\\ &=\Delta_R^{-1}\left(\Delta^{2l}\prod_{i=1}^{l}\left(a_1^{-1}a_2^{-1}\cdots a_{n-2}^{-1}\right)\overline{\beta_{2i-1}}\Delta_L^{-1}\left(a_{n-1}^{-1}a_{n-2}^{-1}\cdots a_{2}^{-1}\right)\beta_{2i}\Delta_R^{-1}\right)\Delta_R, \end{align*} $$
meaning that
![]() $\beta $
is conjugate to
$\beta $
is conjugate to
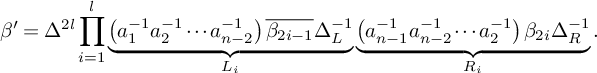 $$\begin{align*}\beta'=\Delta^{2l}\prod_{i=1}^{l}\underbrace{\left(a_1^{-1}a_2^{-1}\cdots a_{n-2}^{-1}\right)\overline{\beta_{2i-1}}\Delta_L^{-1}}_{L_i}\underbrace{\left(a_{n-1}^{-1}a_{n-2}^{-1}\cdots a_{2}^{-1}\right)\beta_{2i}\Delta_R^{-1}}_{R_i}.\end{align*}$$
$$\begin{align*}\beta'=\Delta^{2l}\prod_{i=1}^{l}\underbrace{\left(a_1^{-1}a_2^{-1}\cdots a_{n-2}^{-1}\right)\overline{\beta_{2i-1}}\Delta_L^{-1}}_{L_i}\underbrace{\left(a_{n-1}^{-1}a_{n-2}^{-1}\cdots a_{2}^{-1}\right)\beta_{2i}\Delta_R^{-1}}_{R_i}.\end{align*}$$
Finally, using that homogeneous quasimorphisms are constant on conjugation classes,
![]() ${\omega _*}(\Delta ^2\alpha )=1+{\omega _*}(\alpha )$
(since
${\omega _*}(\Delta ^2\alpha )=1+{\omega _*}(\alpha )$
(since
![]() ${\omega _*}(\alpha \beta )={\omega _*}(\alpha )+{\omega _*}(\beta )$
for commuting
${\omega _*}(\alpha \beta )={\omega _*}(\alpha )+{\omega _*}(\beta )$
for commuting
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
and a homogeneous quasimorphism
$\beta $
and a homogeneous quasimorphism
![]() ${\omega _*}$
), and
${\omega _*}$
), and
![]() ${\omega _*}(\alpha \beta \gamma )\geq {\omega _*}(\alpha \gamma )+{\omega _*}(\beta )-1$
for all n-braids
${\omega _*}(\alpha \beta \gamma )\geq {\omega _*}(\alpha \gamma )+{\omega _*}(\beta )-1$
for all n-braids
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
,
$\beta $
,
![]() $\gamma $
(which follows from
$\gamma $
(which follows from
![]() ${\omega _*}$
having defect at most
${\omega _*}$
having defect at most
![]() $1$
and being constant on conjugation classes), we calculate
$1$
and being constant on conjugation classes), we calculate
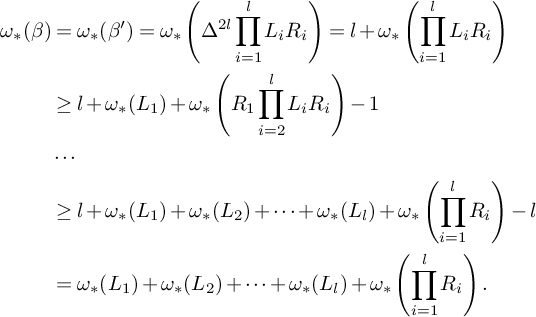 $$ \begin{align*} {\omega_*}(\beta)&={\omega_*}(\beta') ={\omega_*}\left(\Delta^{2l}\prod_{i=1}^{l}L_iR_i\right) =l+{\omega_*}\left(\prod_{i=1}^{l}L_iR_i\right) \\&\geq l+{\omega_*}(L_1)+{\omega_*}\left(R_1\prod_{i=2}^{l}L_iR_i\right)-1 \\&\cdots \\&\geq l+{\omega_*}(L_1)+{\omega_*}(L_2)+\cdots+{\omega_*}(L_l)+{\omega_*}\left(\prod_{i=1}^{l}R_i\right)-l \\&={\omega_*}(L_1)+{\omega_*}(L_2)+\cdots+{\omega_*}(L_l)+{\omega_*}\left(\prod_{i=1}^{l}R_i\right). \end{align*} $$
$$ \begin{align*} {\omega_*}(\beta)&={\omega_*}(\beta') ={\omega_*}\left(\Delta^{2l}\prod_{i=1}^{l}L_iR_i\right) =l+{\omega_*}\left(\prod_{i=1}^{l}L_iR_i\right) \\&\geq l+{\omega_*}(L_1)+{\omega_*}\left(R_1\prod_{i=2}^{l}L_iR_i\right)-1 \\&\cdots \\&\geq l+{\omega_*}(L_1)+{\omega_*}(L_2)+\cdots+{\omega_*}(L_l)+{\omega_*}\left(\prod_{i=1}^{l}R_i\right)-l \\&={\omega_*}(L_1)+{\omega_*}(L_2)+\cdots+{\omega_*}(L_l)+{\omega_*}\left(\prod_{i=1}^{l}R_i\right). \end{align*} $$
Since
![]() ${\omega _*}$
vanishes on braids that can be written without
${\omega _*}$
vanishes on braids that can be written without
![]() $a_1^{\pm 1}$
(which include
$a_1^{\pm 1}$
(which include
![]() $\prod _{i=1}^{l}R_i$
), and thus (by conjugation invariance) also on braids without
$\prod _{i=1}^{l}R_i$
), and thus (by conjugation invariance) also on braids without
![]() $a_{n-1}^{\pm 1}$
(which include
$a_{n-1}^{\pm 1}$
(which include
![]() $L_i$
), we have
$L_i$
), we have
![]() ${\omega _*}(\beta )\geq 0>{\omega _*}(\beta )$
.
${\omega _*}(\beta )\geq 0>{\omega _*}(\beta )$
.
The defect of
![]() ${\omega }$
is known to be
${\omega }$
is known to be
![]() $1$
for
$1$
for
![]() $n\geq 3$
. We provide an argument, which is of the same flavour (but much simpler) than the above proof.
$n\geq 3$
. We provide an argument, which is of the same flavour (but much simpler) than the above proof.
Lemma 10. For
![]() $n\geq 3$
if a homogeneous quasimorphism
$n\geq 3$
if a homogeneous quasimorphism
![]() $f\colon B_n\to \mathbb {R}$
satisfies
$f\colon B_n\to \mathbb {R}$
satisfies
![]() $f\left (B_{n-1}\right )=\{0\}$
, then the defect of f is bounded below by
$f\left (B_{n-1}\right )=\{0\}$
, then the defect of f is bounded below by
![]() $\left |f\left (\Delta ^2\right )\right |$
, that is,
$\left |f\left (\Delta ^2\right )\right |$
, that is,
![]() $\left |f\left (\Delta ^2\right )\right |\leq D_f$
.
$\left |f\left (\Delta ^2\right )\right |\leq D_f$
.
Proof. First, we note that
where the first equality is due to equality of the braids, the second equality uses that
![]() $\Delta ^2$
is in the center and the last equality uses that f vanishes on
$\Delta ^2$
is in the center and the last equality uses that f vanishes on
![]() $\Delta _R\in B_{n-1}\subset B_n$
. Hence, for
$\Delta _R\in B_{n-1}\subset B_n$
. Hence, for
![]() $\alpha =a_2\cdots a_{n-2}a_{n-1}a_{n-1}a_{n-2}\cdots a_2\in B_{n-1}$
and
$\alpha =a_2\cdots a_{n-2}a_{n-1}a_{n-1}a_{n-2}\cdots a_2\in B_{n-1}$
and
![]() $\beta =a_{1}a_{1}$
, we find
$\beta =a_{1}a_{1}$
, we find
where we used that f evaluates to the same on
![]() $a_1a_2\cdots a_{n-2}a_{n-1}a_{n-1}a_{n-2}\cdots a_1$
and its conjugate
$a_1a_2\cdots a_{n-2}a_{n-1}a_{n-1}a_{n-2}\cdots a_1$
and its conjugate
![]() $\alpha \beta $
.
$\alpha \beta $
.
As an aside, we note that the proof of Lemma 10 shows that for
![]() $f={\omega }$
the supremum
$f={\omega }$
the supremum
![]() $D_f$
is attained when
$D_f$
is attained when
![]() $n\geq 3$
.
$n\geq 3$
.
4 Constructions of quasimorphisms and the proof of Proposition 2
In this section, we discuss the existence of many homogeneous quasimorphisms on
![]() $B_n$
for
$B_n$
for
![]() $n\geq 3$
as claimed in Proposition 2. We make use of a geometric group theory setup due to Bestvina and Fujiwara [Reference Bestvina and FujiwaraBF02], which we do not recall in detail. Since this makes this section the least self-contained, we point out that skipping this section can be done at no cost of understanding the results from the introduction except, of course, Proposition 2.
$n\geq 3$
as claimed in Proposition 2. We make use of a geometric group theory setup due to Bestvina and Fujiwara [Reference Bestvina and FujiwaraBF02], which we do not recall in detail. Since this makes this section the least self-contained, we point out that skipping this section can be done at no cost of understanding the results from the introduction except, of course, Proposition 2.
Proposition 2 reduces to the following lemma.
Lemma 11. Let
![]() $n\geq 3$
. There exist an injective
$n\geq 3$
. There exist an injective
![]() $\mathbb {R}$
-linear map
$\mathbb {R}$
-linear map
Here,
![]() $\ell ^1$
denotes the vector space of real-valued sequences
$\ell ^1$
denotes the vector space of real-valued sequences
![]() $\{a_i\}_{n\in N}$
with
$\{a_i\}_{n\in N}$
with
![]() $\sum _{n=1}^\infty |a_i|<\infty $
. Dropping the condition
$\sum _{n=1}^\infty |a_i|<\infty $
. Dropping the condition
![]() $f(B_{n-1})=\{0\}$
, Lemma 11 is known by work of Bestvina and Fujiwara. Indeed, there exist an injective
$f(B_{n-1})=\{0\}$
, Lemma 11 is known by work of Bestvina and Fujiwara. Indeed, there exist an injective
![]() $\mathbb {R}$
-linear map
$\mathbb {R}$
-linear map
by [Reference Bestvina and FujiwaraBF02, Theorem 7 and Proposition 11]. In fact, inspection of their proof reveals that all elements in the image of the
![]() $\mathbb {R}$
-linear map they construct vanish on
$\mathbb {R}$
-linear map they construct vanish on
![]() $B_{n-1}$
. We explain this using the setup, notations and results from [Reference Bestvina and FujiwaraBF02]. We only make use of these in the proof of Lemma 11, and we only invoke Lemma 11 to prove Proposition 2.
$B_{n-1}$
. We explain this using the setup, notations and results from [Reference Bestvina and FujiwaraBF02]. We only make use of these in the proof of Lemma 11, and we only invoke Lemma 11 to prove Proposition 2.
Proof of Lemma 11.
Bestvina and Fujiwara construct a large vector subspace of the vector space of homogeneous quasimorphism on a group G whenever the group G has an action on a
![]() $\delta $
-hyperbolic space X that satisfies weak proper discontinuity (WPD for short) [Reference Bestvina and FujiwaraBF02, Theorem 7]. Actually, Bestvina and Fujiwara construct quasimorphisms that are in general not homogeneous and then consider the quotient of the vector space of quasimorphisms by bounded functions. However, this quotient is readily identified with the vector space of homogeneous quasimorphisms. This identification is given by taking the quasimorphisms
$\delta $
-hyperbolic space X that satisfies weak proper discontinuity (WPD for short) [Reference Bestvina and FujiwaraBF02, Theorem 7]. Actually, Bestvina and Fujiwara construct quasimorphisms that are in general not homogeneous and then consider the quotient of the vector space of quasimorphisms by bounded functions. However, this quotient is readily identified with the vector space of homogeneous quasimorphisms. This identification is given by taking the quasimorphisms
![]() $h_\omega $
from the construction of Bestvina and Fujiwara to their homogenizations
$h_\omega $
from the construction of Bestvina and Fujiwara to their homogenizations
![]() $\widetilde {h_\omega }$
. Under this identification, their construction translates to constructing a subspace of the vector space of homogeneous quasimorphism isomorphic to
$\widetilde {h_\omega }$
. Under this identification, their construction translates to constructing a subspace of the vector space of homogeneous quasimorphism isomorphic to
![]() $\ell ^1$
given by
$\ell ^1$
given by
![]() $\{\sum _{n=1}^\infty a_ib_i\mid \sum _{n=0}^\infty |a_i|<\infty \}$
, where the
$\{\sum _{n=1}^\infty a_ib_i\mid \sum _{n=0}^\infty |a_i|<\infty \}$
, where the
![]() $b_i$
are elements of the form
$b_i$
are elements of the form
![]() $\widetilde {h_\omega }$
.
$\widetilde {h_\omega }$
.
From the construction in [Reference Bestvina and FujiwaraBF02, Section 2] of the homogeneous quasimorphism
![]() ${h_\omega }$
it follows that if an element
${h_\omega }$
it follows that if an element
![]() $r\in G$
has a fixed point
$r\in G$
has a fixed point
![]() $x_0\in X$
, then the homogeneous quasimorphism
$x_0\in X$
, then the homogeneous quasimorphism
![]() $\widetilde {h_\omega }$
vanishes on r. Indeed, choosing
$\widetilde {h_\omega }$
vanishes on r. Indeed, choosing
![]() $x_0$
as the basepoint in their construction of the quasimorphism
$x_0$
as the basepoint in their construction of the quasimorphism
![]() $h_\omega $
, we see that
$h_\omega $
, we see that
![]() $h_\omega (r^k)=0$
for all
$h_\omega (r^k)=0$
for all
![]() $k\in \mathbb {Z}$
. In particular, the homogeneous quasimorphism
$k\in \mathbb {Z}$
. In particular, the homogeneous quasimorphism
![]() $\widetilde {h_\omega }$
satisfies
$\widetilde {h_\omega }$
satisfies ![]() .
.
For technical reasons, we choose our group G to be the quotient ![]() rather than
rather than
![]() $B_n$
. Of course, any quasimorphism on G gives rise to one on
$B_n$
. Of course, any quasimorphism on G gives rise to one on
![]() $B_n$
by composing with the quotient map
$B_n$
by composing with the quotient map
![]() $\pi \colon B_n\to G$
. Thus, by the last paragraph it remains to check that G has an action on a
$\pi \colon B_n\to G$
. Thus, by the last paragraph it remains to check that G has an action on a
![]() $\delta $
-hyperbolic space that satisfies WPD such that the elements of
$\delta $
-hyperbolic space that satisfies WPD such that the elements of
![]() $\pi (B_{n-1})\subset G$
have a fixed point. To do this, we identify
$\pi (B_{n-1})\subset G$
have a fixed point. To do this, we identify
![]() $B_n$
with the mapping class group of the n-punctured disc and we identify
$B_n$
with the mapping class group of the n-punctured disc and we identify
![]() $G=B_n/\langle \Delta ^2\rangle $
with a finite index subgroup of the mapping class group of the
$G=B_n/\langle \Delta ^2\rangle $
with a finite index subgroup of the mapping class group of the
![]() $(n+1)$
-punctured sphere. Then G naturally acts on the curve complex X of the
$(n+1)$
-punctured sphere. Then G naturally acts on the curve complex X of the
![]() $(n+1)$
-punctured sphere. The curve complex X is
$(n+1)$
-punctured sphere. The curve complex X is
![]() $\delta $
-hyperbolic and the action of G on X satisfies WPD since the action of the full mapping class satisfies WPD [Reference Bestvina and FujiwaraBF02, Proposition 11] and restricting an action that satisfies WPD to a finite index subgroup yields an action that satisfies WPD. We conclude the proof by noting that there exists a simple closed curve
$\delta $
-hyperbolic and the action of G on X satisfies WPD since the action of the full mapping class satisfies WPD [Reference Bestvina and FujiwaraBF02, Proposition 11] and restricting an action that satisfies WPD to a finite index subgroup yields an action that satisfies WPD. We conclude the proof by noting that there exists a simple closed curve
![]() $\gamma $
in the
$\gamma $
in the
![]() $(n+1)$
-punctured sphere (in particular,
$(n+1)$
-punctured sphere (in particular,
![]() $[\gamma ]\in X$
) such that
$[\gamma ]\in X$
) such that
![]() $\pi (B_{n-1})=\{[\phi ]\in G\mid [\phi ][\gamma ]=[\gamma ]\}$
. For sake of completeness, we describe such a
$\pi (B_{n-1})=\{[\phi ]\in G\mid [\phi ][\gamma ]=[\gamma ]\}$
. For sake of completeness, we describe such a
![]() $\gamma $
explicitly.
$\gamma $
explicitly.
For this, we make the identification of
![]() $B_{n}$
with the mapping class group of the n-punctured disc D explicit. Here, we taken D to be the closed unit disc in
$B_{n}$
with the mapping class group of the n-punctured disc D explicit. Here, we taken D to be the closed unit disc in
![]() $\mathbb {C}$
with the punctures placed on the open interval
$\mathbb {C}$
with the punctures placed on the open interval
![]() $(-1,1)$
and ordered by the usual order on
$(-1,1)$
and ordered by the usual order on
![]() $(-1,1)\subset \mathbb {R}$
. Namely, we chose an identification isomorphism that sends the generator
$(-1,1)\subset \mathbb {R}$
. Namely, we chose an identification isomorphism that sends the generator
![]() $a_i$
to the mapping class given by a positive half-twist that exchanges the i-th and
$a_i$
to the mapping class given by a positive half-twist that exchanges the i-th and
![]() $(i+1)$
-th punctures and is the identity outside a small neighbourhood of the arc on the real line connecting the i-th and
$(i+1)$
-th punctures and is the identity outside a small neighbourhood of the arc on the real line connecting the i-th and
![]() $(i+1)$
-th puncture. We further identify the
$(i+1)$
-th puncture. We further identify the
![]() $(n+1)$
-punctured sphere with the quotient
$(n+1)$
-punctured sphere with the quotient
![]() $D/S^1$
, where the punctures are as for D with one extra puncture: the point
$D/S^1$
, where the punctures are as for D with one extra puncture: the point
![]() $\infty $
in the quotient corresponding to the collapsed
$\infty $
in the quotient corresponding to the collapsed
![]() $S^1$
. This yields an explicit identification of G with the subgroup of the mapping class group of the
$S^1$
. This yields an explicit identification of G with the subgroup of the mapping class group of the
![]() $(n+1)$
-punctured sphere given by those mapping classes that fix the puncture
$(n+1)$
-punctured sphere given by those mapping classes that fix the puncture
![]() $\infty $
. This identification is such that the quotient map
$\infty $
. This identification is such that the quotient map
![]() $\pi \colon B_n\to G$
is identified with the group homomorphism between the mapping class groups induced by the quotient map
$\pi \colon B_n\to G$
is identified with the group homomorphism between the mapping class groups induced by the quotient map
![]() $D\to D/S^1$
. See, for example, [Reference Hironaka and KinHK06, Reference BirmanBir74] for these identifications.
$D\to D/S^1$
. See, for example, [Reference Hironaka and KinHK06, Reference BirmanBir74] for these identifications.
With this set up, we choose
![]() $\gamma $
to be a simple closed curve in
$\gamma $
to be a simple closed curve in
![]() $D\setminus S^1\subset D/S^1$
that is the boundary of a round disc in
$D\setminus S^1\subset D/S^1$
that is the boundary of a round disc in
![]() $D\setminus S^1$
that contains all but the first puncture. Then, indeed,
$D\setminus S^1$
that contains all but the first puncture. Then, indeed,
![]() $B_{n-1}\subset B_n$
is sent to mapping classes that have a representative that restricts to the identity on
$B_{n-1}\subset B_n$
is sent to mapping classes that have a representative that restricts to the identity on
![]() $\gamma $
.
$\gamma $
.
Proof of Proposition 2.
Fix
![]() $\varepsilon>0$
. And, for
$\varepsilon>0$
. And, for
![]() $r\in \mathbb {R}$
, let
$r\in \mathbb {R}$
, let
![]() $f_r$
be the image of the r-th basis element of a chosen basis for
$f_r$
be the image of the r-th basis element of a chosen basis for
![]() $\ell ^1$
under an injective map guaranteed to exist by Lemma 11. Up to multiplication with a constant, we can arrange for
$\ell ^1$
under an injective map guaranteed to exist by Lemma 11. Up to multiplication with a constant, we can arrange for
![]() $f_r$
to satisfy
$f_r$
to satisfy
![]() $f_r(\Delta ^2)\geq 0$
and
$f_r(\Delta ^2)\geq 0$
and
![]() $D_{f_r}<\varepsilon $
. Define
$D_{f_r}<\varepsilon $
. Define ![]() , and note that
, and note that
![]() $g_r(\Delta ^2)=1$
,
$g_r(\Delta ^2)=1$
,
![]() $g_r(B_{n-1})=\{0\}$
, and
$g_r(B_{n-1})=\{0\}$
, and
![]() $D_{g_r}\leq 1+D_{f_r}<1+\varepsilon $
. Hence, for all but at most one
$D_{g_r}\leq 1+D_{f_r}<1+\varepsilon $
. Hence, for all but at most one
![]() $a\in \mathbb {R}$
,
$a\in \mathbb {R}$
,
![]() $\{g_r\}_{r\in \mathbb {R}\setminus \{a\}}$
is a basis of a subspace of
$\{g_r\}_{r\in \mathbb {R}\setminus \{a\}}$
is a basis of a subspace of
5 The proofs of Theorem 3 and Proposition 5
For the proof of Theorem 3, we use that the FDTC can be expressed in terms of the homogenization of the upsilon invariant. For all
![]() $\beta \in B_n$
and
$\beta \in B_n$
and
![]() $t=\frac {2}{n-1}$
, we have
$t=\frac {2}{n-1}$
, we have
by [Reference Feller and HubbardFH19, Theorem 1.3]. Here, for each
![]() $\beta \in B_n$
and for
$\beta \in B_n$
and for ![]() ,
,
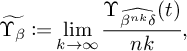
where for a knot K and
![]() $t\in [0,1]$
we denote by
$t\in [0,1]$
we denote by
![]() $\Upsilon _K(t)$
the upsilon invariant introduced in [Reference Ozsváth, Stipsicz and SzabóOSS17]. For more details on homogenization of knot invariants, compare [Reference Gambaudo and GhysGG05, Reference BrandenburskyBra11] and Appendix A. For
$\Upsilon _K(t)$
the upsilon invariant introduced in [Reference Ozsváth, Stipsicz and SzabóOSS17]. For more details on homogenization of knot invariants, compare [Reference Gambaudo and GhysGG05, Reference BrandenburskyBra11] and Appendix A. For
![]() $\Upsilon $
specifically see [Reference Feller and KrcatovichFK17].
$\Upsilon $
specifically see [Reference Feller and KrcatovichFK17].
Recasting
![]() ${\omega }$
using
${\omega }$
using
![]() $\Upsilon $
via Equation (3) allows us to make use of the following slice genus bound. For every knot K, we have
$\Upsilon $
via Equation (3) allows us to make use of the following slice genus bound. For every knot K, we have
As a further input for the proof of Theorem 3, but also the proof of Proposition 5, we need cobordisms with small genera between knots and links arising as connected sums and arising as closures of compositions of braids.
Lemma 12. Let
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
, and
$\beta $
, and
![]() $\gamma $
be in
$\gamma $
be in
![]() $B_n$
.
$B_n$
.
-
(a) There exists a cobordism given by
 $(n-1)$
$(n-1)$
 $1$
-handles between
$1$
-handles between
 $\widehat {\alpha \beta }$
and a connected sum of
$\widehat {\alpha \beta }$
and a connected sum of
 $\widehat {\alpha }$
and
$\widehat {\alpha }$
and
 $\widehat {\beta }$
.
$\widehat {\beta }$
. -
(b) If at least one of the braids
 $\alpha $
,
$\alpha $
,
 $\beta $
or
$\beta $
or
 $\gamma $
is a pure braid, then there exists a cobordism given by
$\gamma $
is a pure braid, then there exists a cobordism given by
 $2(n-1)$
$2(n-1)$
 $1$
-handles between
$1$
-handles between
 $\widehat {\alpha \beta \gamma }$
and
$\widehat {\alpha \beta \gamma }$
and
 $\widehat {\alpha \gamma \beta }$
.
$\widehat {\alpha \gamma \beta }$
.
We remark that, in Equation (a), we do not claim to control which connected sum of
![]() $\widehat {\alpha }$
and
$\widehat {\alpha }$
and
![]() $\widehat {\beta }$
is involved. (Recall that for two links
$\widehat {\beta }$
is involved. (Recall that for two links
![]() $L_1$
and
$L_1$
and
![]() $L_2$
the notion of connected sum
$L_2$
the notion of connected sum
![]() $L_1\#L_2$
depends on a choice of component in each link.) We postpone the proof of Lemma 12 to after its application in the proofs of Theorem 3, where we use Equation (a), and Proposition 5, where we employ Equation (b).
$L_1\#L_2$
depends on a choice of component in each link.) We postpone the proof of Lemma 12 to after its application in the proofs of Theorem 3, where we use Equation (a), and Proposition 5, where we employ Equation (b).
For the proof of Theorem 3, we observe that there exists a cobordism consisting of
![]() $(n-1)nk$
$(n-1)nk$
![]() $1$
-handles between
$1$
-handles between
![]() $\widehat {\beta ^{nk}\delta }$
and a
$\widehat {\beta ^{nk}\delta }$
and a
![]() $nk$
-fold connected sum of
$nk$
-fold connected sum of
![]() $\widehat {\beta }$
; we denote the latter by
$\widehat {\beta }$
; we denote the latter by
![]() $nk\widehat {\beta }$
. Indeed, by concatenation of
$nk\widehat {\beta }$
. Indeed, by concatenation of
![]() $nk$
cobordism as provided by Lemma 12(a), we find such a cobordism between
$nk$
cobordism as provided by Lemma 12(a), we find such a cobordism between
![]() $\widehat {\beta ^{nk}\delta }$
and a connected sum of
$\widehat {\beta ^{nk}\delta }$
and a connected sum of
![]() $nk$
many
$nk$
many
![]() $\widehat {\beta }$
and one
$\widehat {\beta }$
and one
![]() $\widehat {\delta }$
(which is an unknot) as desired; compare also [Reference Feller and HubbardFH19, Appendix A]. In particular, we have
$\widehat {\delta }$
(which is an unknot) as desired; compare also [Reference Feller and HubbardFH19, Appendix A]. In particular, we have
where the second inequality follows from
![]() $1-\chi _4$
being subadditive under connected sum.
$1-\chi _4$
being subadditive under connected sum.
Proof of Theorem 3.
Set
![]() $t=\frac {2}{n-1}$
. For every
$t=\frac {2}{n-1}$
. For every
![]() $\beta \in B_n$
, we have
$\beta \in B_n$
, we have
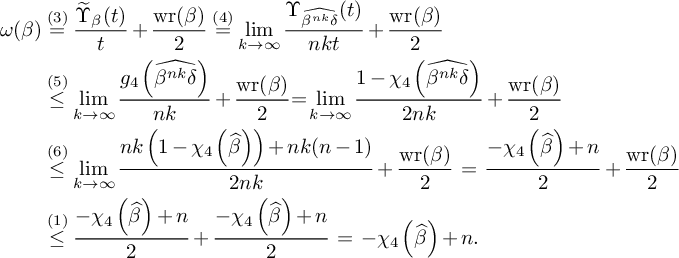 $$ \begin{align*} {\omega}(\beta)&\overset{(3)} {=}\frac{\widetilde{\Upsilon}_\beta(t)}{t}+\frac{\mathrm{{wr}}(\beta)}{2} \overset{\text{(4)}} {=}\lim_{k\to\infty}\frac{\Upsilon_{\widehat{\beta^{nk}\delta}}(t)}{nkt}+\frac{\mathrm{{wr}}(\beta)}{2} \\& \overset{\text{(5)}}{\leq} \lim_{k\to\infty}\frac{g_4\left(\widehat{\beta^{nk}\delta}\right)}{nk}+\frac{\mathrm{{wr}}(\beta)}{2} {=}\lim_{k\to\infty}\frac{1-\chi_4\left(\widehat{\beta^{nk}\delta}\right)}{2nk}+\frac{\mathrm{{wr}}(\beta)}{2} \\& \overset{\text{(6)}}{\leq}\lim_{k\to\infty} \frac{nk\left(1-\chi_4\left(\widehat{\beta}\right)\right)+nk(n-1)}{2nk}+\frac{\mathrm{{wr}}(\beta)}{2} \overset{\phantom{\text{(6)}}} {=}\frac{-\chi_4\left(\widehat{\beta}\right)+n}{2}+\frac{\mathrm{{wr}}(\beta)}{2}\\ & \overset{\text{(1)}}{\leq} \frac{-\chi_4\left(\widehat{\beta}\right)+n}{2}+\frac{-\chi_4\left(\widehat{\beta}\right)+n}{2} \overset{\phantom{\text{(1)}}}{=}-\chi_4\left(\widehat{\beta}\right)+n.\\[-37pt] \end{align*} $$
$$ \begin{align*} {\omega}(\beta)&\overset{(3)} {=}\frac{\widetilde{\Upsilon}_\beta(t)}{t}+\frac{\mathrm{{wr}}(\beta)}{2} \overset{\text{(4)}} {=}\lim_{k\to\infty}\frac{\Upsilon_{\widehat{\beta^{nk}\delta}}(t)}{nkt}+\frac{\mathrm{{wr}}(\beta)}{2} \\& \overset{\text{(5)}}{\leq} \lim_{k\to\infty}\frac{g_4\left(\widehat{\beta^{nk}\delta}\right)}{nk}+\frac{\mathrm{{wr}}(\beta)}{2} {=}\lim_{k\to\infty}\frac{1-\chi_4\left(\widehat{\beta^{nk}\delta}\right)}{2nk}+\frac{\mathrm{{wr}}(\beta)}{2} \\& \overset{\text{(6)}}{\leq}\lim_{k\to\infty} \frac{nk\left(1-\chi_4\left(\widehat{\beta}\right)\right)+nk(n-1)}{2nk}+\frac{\mathrm{{wr}}(\beta)}{2} \overset{\phantom{\text{(6)}}} {=}\frac{-\chi_4\left(\widehat{\beta}\right)+n}{2}+\frac{\mathrm{{wr}}(\beta)}{2}\\ & \overset{\text{(1)}}{\leq} \frac{-\chi_4\left(\widehat{\beta}\right)+n}{2}+\frac{-\chi_4\left(\widehat{\beta}\right)+n}{2} \overset{\phantom{\text{(1)}}}{=}-\chi_4\left(\widehat{\beta}\right)+n.\\[-37pt] \end{align*} $$
Proof of Proposition 5.
Fix
![]() $\varepsilon>0$
, and let
$\varepsilon>0$
, and let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be n-braids such that
$\beta $
be n-braids such that
![]() $f(\alpha \beta )-f(\alpha )-f(\beta )\geq D_f-\varepsilon $
. We first note that we can and do assume that
$f(\alpha \beta )-f(\alpha )-f(\beta )\geq D_f-\varepsilon $
. We first note that we can and do assume that
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are pure braids. Indeed, if not, pick
$\beta $
are pure braids. Indeed, if not, pick
![]() $\alpha '$
and
$\alpha '$
and
![]() $\beta '$
such that
$\beta '$
such that
![]() $f(\alpha '\beta ')-f(\alpha ')-f(\beta ')\geq D_f-\varepsilon /n$
and set
$f(\alpha '\beta ')-f(\alpha ')-f(\beta ')\geq D_f-\varepsilon /n$
and set ![]() and
and ![]() . Combining
. Combining
with
![]() $|f((ab)^n)-f(a^nb^n)|\leq (n-1)D_f$
, which one checks by iteratively applying
$|f((ab)^n)-f(a^nb^n)|\leq (n-1)D_f$
, which one checks by iteratively applying
we have that
![]() $f(\alpha \beta )-f(\alpha )-f(\beta )\geq D_f-\varepsilon $
.
$f(\alpha \beta )-f(\alpha )-f(\beta )\geq D_f-\varepsilon $
.
Fix an even positive integer k. Using that f is homogeneous and that
![]() $f(ab)-f(a)-f(b)\leq D_f$
for all
$f(ab)-f(a)-f(b)\leq D_f$
for all
![]() $a,b\in B_n$
, we calculate
$a,b\in B_n$
, we calculate
 $$ \begin{align*} kD_f-k\varepsilon&\leq k(f(\alpha\beta)-f(\alpha)-f(\beta))=f \left((\alpha\beta)^{k}\right)+f\left(\alpha^{-k}\right)+f\left(\beta^{-k}\right)\\ &\leq f\left((\alpha\beta)^{k}\alpha^{-k}\right)+D_f+f\left(\beta^{-k}\right)\\ &\leq f\left((\alpha\beta)^{k}\alpha^{-k}\beta^{-k}\right)+D_f+D_f\\ &\leq f\left((\alpha\beta)^{k}\alpha^{-k}\beta^{-k}\delta\right)-f(\delta)+D_f+D_f+D_f\\ &\leq Ag_4(K)+C-f(\delta)+D_f+D_f+D_f, \end{align*} $$
$$ \begin{align*} kD_f-k\varepsilon&\leq k(f(\alpha\beta)-f(\alpha)-f(\beta))=f \left((\alpha\beta)^{k}\right)+f\left(\alpha^{-k}\right)+f\left(\beta^{-k}\right)\\ &\leq f\left((\alpha\beta)^{k}\alpha^{-k}\right)+D_f+f\left(\beta^{-k}\right)\\ &\leq f\left((\alpha\beta)^{k}\alpha^{-k}\beta^{-k}\right)+D_f+D_f\\ &\leq f\left((\alpha\beta)^{k}\alpha^{-k}\beta^{-k}\delta\right)-f(\delta)+D_f+D_f+D_f\\ &\leq Ag_4(K)+C-f(\delta)+D_f+D_f+D_f, \end{align*} $$
where K denotes the closure of
![]() $(\alpha \beta )^{k}\alpha ^{-k}\beta ^{-k}\delta $
and, as above,
$(\alpha \beta )^{k}\alpha ^{-k}\beta ^{-k}\delta $
and, as above,
![]() $\delta =a_1\cdots a_{n-1}$
. Note that K is a knot since
$\delta =a_1\cdots a_{n-1}$
. Note that K is a knot since
![]() $(\alpha \beta )^{k}\alpha ^{-k}\beta ^{-k}$
is a pure braid.
$(\alpha \beta )^{k}\alpha ^{-k}\beta ^{-k}$
is a pure braid.
Next, we observe that there exists a cobordism of genus
![]() $\frac {k}{2}(n-1)$
between K and the closure of
$\frac {k}{2}(n-1)$
between K and the closure of
![]() $\beta ^{k}\alpha ^{k}\alpha ^{-k}\beta ^{-k}\delta =\delta $
.
$\beta ^{k}\alpha ^{k}\alpha ^{-k}\beta ^{-k}\delta =\delta $
.
For this, we write
![]() $(\alpha \beta )^{k}\alpha ^{-k}\beta ^{-k}$
as a product of
$(\alpha \beta )^{k}\alpha ^{-k}\beta ^{-k}$
as a product of
![]() $\frac {k}{2}$
commutators of pure braids, that is,
$\frac {k}{2}$
commutators of pure braids, that is,
![]() $(\alpha \beta )^{k}\alpha ^{-k}\beta ^{-k}=[\alpha _1,\beta _1][\alpha _2,\beta _2]\cdots [\alpha _{\frac {k}{2}},\beta _{\frac {k}{2}}]$
for some pure braids
$(\alpha \beta )^{k}\alpha ^{-k}\beta ^{-k}=[\alpha _1,\beta _1][\alpha _2,\beta _2]\cdots [\alpha _{\frac {k}{2}},\beta _{\frac {k}{2}}]$
for some pure braids
![]() $\alpha _i,\beta _i\in B_n$
. This is possible by [Reference CalegariCal09, Proof of Lemma 2.24]; compare also [Reference BavardBav91].Footnote
2
$\alpha _i,\beta _i\in B_n$
. This is possible by [Reference CalegariCal09, Proof of Lemma 2.24]; compare also [Reference BavardBav91].Footnote
2
By Lemma 12(b), for all
![]() $b\in B_n$
the closures of
$b\in B_n$
the closures of
![]() $[\alpha _i,\beta _i]b=\alpha _i\beta _i\alpha _i^{-1}\beta _i^{-1}b$
and
$[\alpha _i,\beta _i]b=\alpha _i\beta _i\alpha _i^{-1}\beta _i^{-1}b$
and
![]() $\beta _i\alpha _i\alpha _i^{-1}\beta _i^{-1}b=b$
are related by a cobordism with
$\beta _i\alpha _i\alpha _i^{-1}\beta _i^{-1}b=b$
are related by a cobordism with
![]() $2(n-1)$
$2(n-1)$
![]() $1$
-handles, hence applying this
$1$
-handles, hence applying this
![]() $\frac {k}{2}$
times gives a cobordism between K and the closure of
$\frac {k}{2}$
times gives a cobordism between K and the closure of
![]() $\delta $
given by
$\delta $
given by
![]() $k(n-1)$
$k(n-1)$
![]() $1$
-handles. In other words, we have a cobordism of genus
$1$
-handles. In other words, we have a cobordism of genus
![]() $\frac {k}{2}(n-1)$
as desired.
$\frac {k}{2}(n-1)$
as desired.
Since
![]() $\delta $
has the unknot as its closure, we have
$\delta $
has the unknot as its closure, we have
![]() $g_4(K)\leq \frac {k}{2}(n-1)$
by the last paragraph. We conclude that
$g_4(K)\leq \frac {k}{2}(n-1)$
by the last paragraph. We conclude that
which yields
![]() $D_f\leq \frac {A}{2}(n-1)$
by first dividing by k and taking the limit
$D_f\leq \frac {A}{2}(n-1)$
by first dividing by k and taking the limit
![]() $k\to \infty $
and then letting
$k\to \infty $
and then letting
![]() $\varepsilon $
tend to 0.
$\varepsilon $
tend to 0.
Finally, we turn to the proof of Lemma 12. The idea of the proof is of a similar flavour as the arguments used in [Reference BrandenburskyBra11] and [Reference Feller and HubbardFH19, Appendix A], but to the best of our knowledge, the exact statement does not yet appear in the literature.
Proof of Lemma 12.
To see Equation (a), consider a diagram for
![]() $\widehat {\alpha \beta }$
as depicted in Figure 1 A) (where
$\widehat {\alpha \beta }$
as depicted in Figure 1 A) (where
![]() $\gamma $
is taken to be the trivial braid) and apply
$\gamma $
is taken to be the trivial braid) and apply
![]() $(n-1)$
handle moves, starting with the one indicated by the blackboard framed dotted (green) arc, to find the diagram in Figure 1 B). The link given by this diagram is a connected sum of
$(n-1)$
handle moves, starting with the one indicated by the blackboard framed dotted (green) arc, to find the diagram in Figure 1 B). The link given by this diagram is a connected sum of
![]() $\widehat {\alpha }$
and
$\widehat {\alpha }$
and
![]() $\widehat {\alpha \beta }$
with respect to the indicated sphere (red); hence, we have that there exists a cobordism between
$\widehat {\alpha \beta }$
with respect to the indicated sphere (red); hence, we have that there exists a cobordism between
![]() $\widehat {\alpha \beta }$
and the connected sum of
$\widehat {\alpha \beta }$
and the connected sum of
![]() $\widehat {\alpha }$
and
$\widehat {\alpha }$
and
![]() $\widehat {\alpha \beta }$
depicted in Figure 1 B).
$\widehat {\alpha \beta }$
depicted in Figure 1 B).
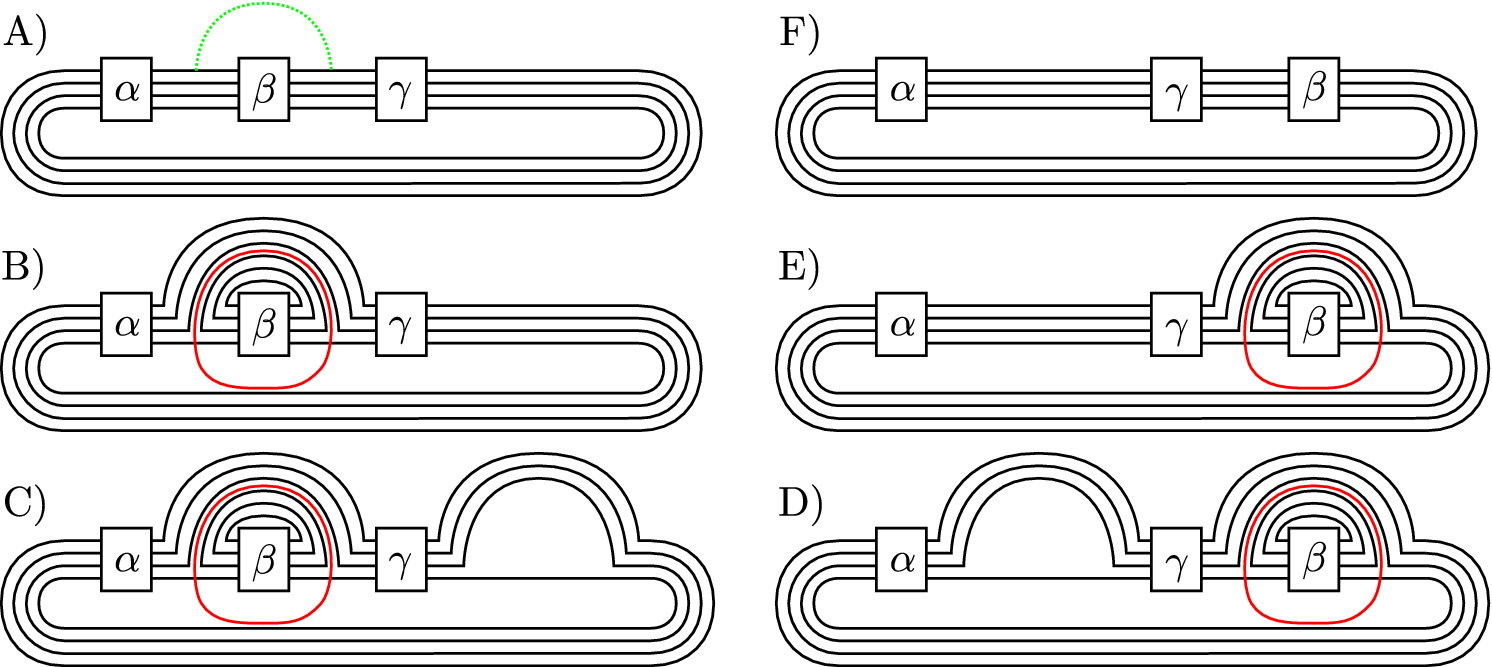
Figure 1 Isotopies and cobordisms proving Lemma 12. For readability of the diagrams the illustration is for
![]() $n=4$
.
$n=4$
.
We turn to Equation (b). Since
![]() $\alpha \beta \gamma $
,
$\alpha \beta \gamma $
,
![]() $\beta \gamma \alpha $
, and
$\beta \gamma \alpha $
, and
![]() $\gamma \alpha \beta $
all are conjugate and hence have the same closure, we may and do assume that
$\gamma \alpha \beta $
all are conjugate and hence have the same closure, we may and do assume that
![]() $\gamma $
is a pure braid. Consider a diagram for
$\gamma $
is a pure braid. Consider a diagram for
![]() $\widehat {\alpha \beta }$
as depicted in Figure 1 A) and apply
$\widehat {\alpha \beta }$
as depicted in Figure 1 A) and apply
![]() $(n-1)$
handle moves to find the diagram in Figure 1 B) as in the proof of Equation (a). Figure 1 B) and Figure 1 C) depict isotopic links (in fact the diagrams are the same up to isotopy of the plane). Figure 1 C) and Figure 1 D) depict isotopic links. An isotopy is given by shrinking and moving the summand
$(n-1)$
handle moves to find the diagram in Figure 1 B) as in the proof of Equation (a). Figure 1 B) and Figure 1 C) depict isotopic links (in fact the diagrams are the same up to isotopy of the plane). Figure 1 C) and Figure 1 D) depict isotopic links. An isotopy is given by shrinking and moving the summand
![]() $\widehat {\beta }$
through
$\widehat {\beta }$
through
![]() $\gamma $
(here, we invoke that
$\gamma $
(here, we invoke that
![]() $\gamma $
is a pure braid). Finally, Figure 1 D) and Figure 1 E) depict isotopic links and
$\gamma $
is a pure braid). Finally, Figure 1 D) and Figure 1 E) depict isotopic links and
![]() $(n-1)$
handle moves turn the diagram given in Figure 1 E) into the one given in Figure 1 F). All in all, we find that there exists a cobordism given by
$(n-1)$
handle moves turn the diagram given in Figure 1 E) into the one given in Figure 1 F). All in all, we find that there exists a cobordism given by
![]() $2(n-1)$
$2(n-1)$
![]() $1$
-handles between
$1$
-handles between
![]() $\widehat {\alpha \beta \gamma }$
and
$\widehat {\alpha \beta \gamma }$
and
![]() $\widehat {\alpha \gamma \beta }$
as desired.
$\widehat {\alpha \gamma \beta }$
as desired.
Appendix A The slice-Bennequin inequality for the homogenization of 1-Lipschitz concordance homomorphisms
In this appendix, we explain that the homogenization of a 1-Lipschitz concordance homomorphism satisfies a version of the slice-Bennequin inequality. This can be understood as providing a common framework for both the slice-Bennequin inequality (1) and Theorem 3; see Examples 14 and 15, respectively. What follows below is based on the same idea as the proof of Theorem 3, which was rather straightforward once the necessary preparations (like Lemma 12) are made. Still, we think it is worth making this explicit as the exact statement and perspective appear to be absent from the literature. What follows owes a lot to the ideas of homogenization of concordance homomorphisms as pursued in [Reference Gambaudo and GhysGG05] for Tristram–Levine signatures and in general in [Reference BrandenburskyBra11] and the idea of proof of the slice-Bennequin inequality as pioneered by Rudolph [Reference RudolphRud93].
We call a real-valued knot invariant
![]() $I\colon \mathfrak {K}nots\to \mathbb {R}$
a
$I\colon \mathfrak {K}nots\to \mathbb {R}$
a
![]() $1$
-Lipschitz concordance homomorphism, if
$1$
-Lipschitz concordance homomorphism, if
![]() $I(K\#J)=I(K)+I(J)$
and
$I(K\#J)=I(K)+I(J)$
and
![]() $|I(K)|\leq g_4(K)$
for all
$|I(K)|\leq g_4(K)$
for all
![]() $K,J\in \mathfrak {K}nots$
, where
$K,J\in \mathfrak {K}nots$
, where
![]() $\mathfrak {K}nots$
denotes the set of isotopy classes of knots. (As ‘concordance homomorphism’ in the name suggests, such I factor through the smooth concordance group and the induced map is a group homomorphism.) Writing
$\mathfrak {K}nots$
denotes the set of isotopy classes of knots. (As ‘concordance homomorphism’ in the name suggests, such I factor through the smooth concordance group and the induced map is a group homomorphism.) Writing ![]() as above, for each
as above, for each
![]() $1$
-Lipschitz concordance homomorphism I, we have that
$1$
-Lipschitz concordance homomorphism I, we have that
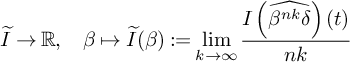
is a homogeneous quasimorphism with defect
![]() $D\leq \frac {n-1}{2}$
; see [Reference Feller and HubbardFH19, Lemma A.1].
$D\leq \frac {n-1}{2}$
; see [Reference Feller and HubbardFH19, Lemma A.1].
Lemma 13. Fix an integer
![]() $1\geq n$
. For all
$1\geq n$
. For all
![]() $\beta \in B_n$
, we have
$\beta \in B_n$
, we have
![]() $\widetilde {I}(\beta )\leq \frac { -\chi _4\left (\widehat {\beta }\right )+n}{2}$
.
$\widetilde {I}(\beta )\leq \frac { -\chi _4\left (\widehat {\beta }\right )+n}{2}$
.
Proof.
![]() $\widetilde {I}(\beta ) \overset {\text {(7)}} {=}\lim _{k\to \infty }\frac {I\left (\widehat {\beta ^{nk}\delta }\right )}{nk}{\leq } \lim _{k\to \infty }\frac {g_4\left (\widehat {\beta ^{nk}\delta }\right )}{nk} {=}\lim _{k\to \infty }\frac {1-\chi _4\left (\widehat {\beta ^{nk}\delta }\right )}{2nk} $
$\widetilde {I}(\beta ) \overset {\text {(7)}} {=}\lim _{k\to \infty }\frac {I\left (\widehat {\beta ^{nk}\delta }\right )}{nk}{\leq } \lim _{k\to \infty }\frac {g_4\left (\widehat {\beta ^{nk}\delta }\right )}{nk} {=}\lim _{k\to \infty }\frac {1-\chi _4\left (\widehat {\beta ^{nk}\delta }\right )}{2nk} $
![]() $\phantom{\text{(1)}\text{(1)}\text{(1)},,}\overset {\text {(6)}}{\leq }\lim _{k\to \infty } \frac {nk\left (1-\chi _4\left (\widehat {\beta }\right )\right )+nk(n-1)}{2nk} \overset {\phantom {\text {(1)}}} {=}\frac {-\chi _4\left (\widehat {\beta }\right )+n}{2}.$
$\phantom{\text{(1)}\text{(1)}\text{(1)},,}\overset {\text {(6)}}{\leq }\lim _{k\to \infty } \frac {nk\left (1-\chi _4\left (\widehat {\beta }\right )\right )+nk(n-1)}{2nk} \overset {\phantom {\text {(1)}}} {=}\frac {-\chi _4\left (\widehat {\beta }\right )+n}{2}.$
In case
![]() $\beta \in B_n$
has a knot as its closure
$\beta \in B_n$
has a knot as its closure
![]() $\widehat {\beta }$
, then
$\widehat {\beta }$
, then
![]() $\left |I\left (\widehat {\beta }\right )-\widetilde {I}(\beta )\right |\leq \frac {n-1}{2}$
(this follows readily from Lemma 12; it is explicitly stated in [Reference Feller and HubbardFH19, Lemma A.1]), hence
$\left |I\left (\widehat {\beta }\right )-\widetilde {I}(\beta )\right |\leq \frac {n-1}{2}$
(this follows readily from Lemma 12; it is explicitly stated in [Reference Feller and HubbardFH19, Lemma A.1]), hence
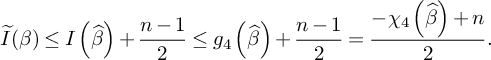 $$ \begin{align} \widetilde{I}(\beta)\leq I\left(\widehat{\beta}\right)+\frac{n-1}{2}\leq g_4\left(\widehat{\beta}\right)+\frac{n-1}{2}=\frac{ -\chi_4\left(\widehat{\beta}\right)+n}{2}. \end{align} $$
$$ \begin{align} \widetilde{I}(\beta)\leq I\left(\widehat{\beta}\right)+\frac{n-1}{2}\leq g_4\left(\widehat{\beta}\right)+\frac{n-1}{2}=\frac{ -\chi_4\left(\widehat{\beta}\right)+n}{2}. \end{align} $$
Example 14. We consider the case when I is a slice torus invariant – a 1-Lipschitz concordance homomorphism I with
![]() $I(T_{p,p+1})=g_4(T_{p,p+1})=(p-1)p/2$
for positive integers p. Slice torus invariants include Ozsváth-Szabó’s
$I(T_{p,p+1})=g_4(T_{p,p+1})=(p-1)p/2$
for positive integers p. Slice torus invariants include Ozsváth-Szabó’s
![]() $\tau $
[Reference Ozsváth and SzabóOS03] and Rasumussen’s s [Reference RasmussenRas10]. In this case, we have
$\tau $
[Reference Ozsváth and SzabóOS03] and Rasumussen’s s [Reference RasmussenRas10]. In this case, we have
![]() $\widetilde {I}=\mathrm {{wr}}/2$
; see, for example, [Reference Feller and HubbardFH19, Lemma A.3]. Hence, for such I, Lemma 13 recovers Equation (1), and Equation (8) reads, for all
$\widetilde {I}=\mathrm {{wr}}/2$
; see, for example, [Reference Feller and HubbardFH19, Lemma A.3]. Hence, for such I, Lemma 13 recovers Equation (1), and Equation (8) reads, for all
![]() $\beta \in B_n$
with closure a knot,
$\beta \in B_n$
with closure a knot,
We find this to be philosophically pleasing for the following reason. Observe that slice torus invariants are by definition the 1-Lipschitz concordance homomorphisms that are strong enough to reprove the local Thom conjecture (since the latter can be phrased as
![]() $g_4(T_{p,p+1})=(p-1)p/2$
for all positive integers p [Reference Kronheimer and MrowkaKM93, Corollary 1.3]). In fact, the existence of slice torus invariants can be seen to be equivalent to the statement of the local Thom conjecture without making use of any explicit construction of such an invariant [Reference Feller, Lewark and LobbFLL22, Remark 4]. It is then fitting that, via homogenization, slice torus invariants recover the slice-Bennequin inequality, which Rudolph derived by elementary means using only the local Thom conjecture as an input.
$g_4(T_{p,p+1})=(p-1)p/2$
for all positive integers p [Reference Kronheimer and MrowkaKM93, Corollary 1.3]). In fact, the existence of slice torus invariants can be seen to be equivalent to the statement of the local Thom conjecture without making use of any explicit construction of such an invariant [Reference Feller, Lewark and LobbFLL22, Remark 4]. It is then fitting that, via homogenization, slice torus invariants recover the slice-Bennequin inequality, which Rudolph derived by elementary means using only the local Thom conjecture as an input.
Example 15. If ![]() , then
, then
![]() $\widetilde {I}=2{\omega }$
by Equation (3). Hence, Lemma 13 yields Theorem 3, and Equation (8) reads, for all
$\widetilde {I}=2{\omega }$
by Equation (3). Hence, Lemma 13 yields Theorem 3, and Equation (8) reads, for all
![]() $\beta \in B_n$
with closure a knot,
$\beta \in B_n$
with closure a knot,
 $$\begin{align*}{\omega}(\beta)\leq \frac{2\Upsilon_{\widehat{\beta}}(\frac{2}{n-1})}{n-1}+\tau\left(\widehat{\beta}\right)+n-1\leq 2g_4\left(\widehat{\beta}\right)+{n-1}.\end{align*}$$
$$\begin{align*}{\omega}(\beta)\leq \frac{2\Upsilon_{\widehat{\beta}}(\frac{2}{n-1})}{n-1}+\tau\left(\widehat{\beta}\right)+n-1\leq 2g_4\left(\widehat{\beta}\right)+{n-1}.\end{align*}$$
In light of Equation (8), we wonder whether every homogeneous quasimorphism that satisfies a slice-Bennequin inequality does arise as a homogenization.
Question 16. Fix
![]() $n\geq 3$
, and let
$n\geq 3$
, and let
![]() $f\colon B_n\to \mathbb {R}$
be a homogeneous quasimorphism. If there exist constants
$f\colon B_n\to \mathbb {R}$
be a homogeneous quasimorphism. If there exist constants
![]() $A,C\in \mathbb {R}$
such that
$A,C\in \mathbb {R}$
such that
does there exist a 1-Lipschitz concordance homomorphism I and
![]() $r\in \mathbb {R}$
such that
$r\in \mathbb {R}$
such that
![]() $f=r\widetilde {I}$
?
$f=r\widetilde {I}$
?
In light of the fact that Question 8, as far as we know, remains open, it seems that even a positive answer to the following is possible.
Question 17. Fix
![]() $n\geq 3$
, and let
$n\geq 3$
, and let
![]() $f\colon B_n\to \mathbb {R}$
be a homogeneous quasimorphism. Does there exist a 1-Lipschitz concordance homomorphism I and
$f\colon B_n\to \mathbb {R}$
be a homogeneous quasimorphism. Does there exist a 1-Lipschitz concordance homomorphism I and
![]() $r\in \mathbb {R}$
such that
$r\in \mathbb {R}$
such that
![]() $f=r\widetilde {I}$
?
$f=r\widetilde {I}$
?
This author strongly suspects that the answer to Question 17 is no, but is unable to provide a counterexample.
Acknowledgements.
The author thanks Jonathan Bowden, Francesco Fournier-Facio and Alessandro Sisto for helpful conversations concerning the construction of quasimorphisms via actions on
![]() $\delta $
-hyperbolic spaces that satisfy WPD. The author also thanks Tetsuya Ito for a stimulating exchange and an improvement concerning Proposition 5. And the author is grateful to the anonymous referee for carefully reading the text and providing helpful comments. Finally, the author gratefully acknowledges support by the SNSF Grant 181199.
$\delta $
-hyperbolic spaces that satisfy WPD. The author also thanks Tetsuya Ito for a stimulating exchange and an improvement concerning Proposition 5. And the author is grateful to the anonymous referee for carefully reading the text and providing helpful comments. Finally, the author gratefully acknowledges support by the SNSF Grant 181199.