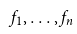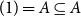A foundation for synthetic algebraic geometry

Abstract

This is a foundation for algebraic geometry, developed internal to the Zariski topos, building on the work of Kock and Blechschmidt (Kock (2006) [I.12], Blechschmidt (2017)). The Zariski topos consists of sheaves on the site opposite to the category of finitely presented algebras over a fixed ring, with the Zariski topology, that is, generating covers are given by localization maps for finitely many elements $f_1,\dots, f_n$ that generate the ideal $(1)=A\subseteq A$. We use homotopy-type theory together with three axioms as the internal language of a (higher) Zariski topos. One of our main contributions is the use of higher types – in the homotopical sense – to define and reason about cohomology. Actually computing cohomology groups seems to need a principle along the lines of our “Zariski local choice” axiom, which we justify as well as the other axioms using a cubical model of homotopy-type theory.

Introduction

Algebraic geometry is the study of solutions of polynomial equations using methods from geometry. The central geometric objects in algebraic geometry are called schemes. Their basic building blocks are called affine schemes, where, informally, an affine scheme corresponds to a solution sets of polynomial equations. While this correspondence is clearly visible in the functorial approach to algebraic geometry and our synthetic approach, it is somewhat obfuscated in the most commonly used, topological approach.

In recent years, computer formalization of the intricate notion of affine schemes received some attention as a benchmark problem – this is, however, not a problem addressed by this work. Instead, we use a synthetic approach to algebraic geometry, very much alike to that of synthetic differential geometry. This means, while a scheme in classical algebraic geometry is a complicated compound datum, we work in a setting, based on homotopy type theory, where schemes are types, with an additional property that can be defined within our synthetic theory.

Following ideas of Ingo Blechschmidt and Anders Kock (Blechschmidt (2017); Kock (2006)[I.12]), we use a base ring $R$ , which is local and satisfies an axiom reminiscent of the Kock–Lawvere axiom. This more general axiom is called synthetic quasi coherence (SQC) by Blechschmidt and a version quantifying over external algebras is called the comprehensive axiom ¹ by Kock. The exact concise form of the SQC axiom we use was noted by David Jaz Myers in 2018 and communicated to the first author.

Before we state the SQC axiom, let us take a step back and look at the basic objects of study in algebraic geometry, solutions of polynomial equations. Given a system of polynomial equations

\begin{align*} p_1(X_1, \dots, X_n) &= 0\rlap{,} \\ \vdots \quad \quad \;\; \\ p_m(X_1, \dots, X_n) &= 0\rlap{,} \end{align*}

the solution set $\{\, x : R^n \mid \forall i.\; p_i(x_1, \dots, x_n) = 0 \,\}$ is in canonical bijection to the set of $R$ -algebra homomorphisms

\begin{equation*} {\mathrm {Hom}}_{R\text {-}\mathrm {Alg}}(R[X_1, \dots, X_n]/(p_1, \dots, p_m), R) \end{equation*}

by identifying a solution $(x_1,\dots, x_n)$ with the homomorphism that maps each $X_i$ to $x_i$ . Conversely, for any $R$ -algebra $A$ which is merely of the form $R[X_1, \dots, X_n]/(p_1, \dots, p_m)$ , we define the spectrum of $A$ to be

\begin{equation*} \mathrm {Spec}\;A \;\colon \!\!\!\equiv\; {\mathrm {Hom}}_{R\text {-}\mathrm {Alg}}(A, R) \rlap {.} \end{equation*}

In contrast to classical, nonsynthetic algebraic geometry, where this set needs to be equipped with additional structure, we postulate axioms that will ensure that $\mathrm{Spec}\;A$ has the expected geometric properties. Namely, SQC is the statement that, for all finitely presented ² $R$ -algebras $A$ , the canonical map

\begin{align*} A&\xrightarrow{\sim } (\mathrm{Spec}\;A\to R) \\ a&\mapsto (\varphi \mapsto \varphi (a)) \end{align*}

is an equivalence. A prime example of a spectrum is ${\mathbb{A}}^1\;\colon \!\!\!\equiv\; \mathrm{Spec}\; R[X]$ , which turns out to be the underlying set of $R$ . With the SQC axiom, any function $f:{\mathbb{A}}^1\to{\mathbb{A}}^1$ is given as a polynomial with coefficients in $R$ . In fact, all functions between affine schemes are given by polynomials. Furthermore, for any affine scheme $\mathrm{Spec}\;A$ , the axiom ensures that the algebra $A$ can be reconstructed as the algebra of functions $\mathrm{Spec}\;A \to R$ , therefore establishing a duality between affine schemes and algebras.

The Kock–Lawvere axiom used in synthetic differential geometry might be stated as the SQC axiom restricted to (external) Weil-algebras, whose spectra correspond to pointed infinitesimal spaces. These spaces can be used in both synthetic differential and algebraic geometry in very much the same way.

In the accompanying formalization Cherubini and Hutzler (3) of some basic results, we use a setup which was already proposed by David Jaz Myers in a conference talk (Myers (2019b ,a)). On top of Myers’ ideas, we were able to define schemes, develop some topological properties of schemes, and construct projective space.

An important, not yet formalized result is the construction of cohomology groups. This is where the homotopy type theory provides a considerable advantage – instead of the usual approach to cohomology based on homological algebra, we develop the theory using higher types, for example, the $n$ -th Eilenberg–MacLane space $K(R,n)$ of the group $(R,+)$ . As an analog of classical cohomology with values in the structure sheaf, we then define cohomology with coefficients in the base ring as

\begin{equation*} H^n(X,R):\equiv \lVert X\to K(R,n) \rVert _0 \rlap {.} \end{equation*}

This definition is very convenient for proving abstract properties of cohomology. For concrete calculations, we make use of another axiom, which we call Zariski-local choice. While this axiom was conceived of for exactly these kind of calculations, it turned out to settle numerous questions with no apparent connection to cohomology. One example is the equivalence of two notions of open subspace. A pointwise definition of openness was suggested to us by Ingo Blechschmidt and is very convenient to work with. However, classically, basic open subsets of an affine scheme are given by functions on the scheme and the corresponding open is morally the collection of points where the function does not vanish. With Zariski-local choice, we were able to show that these notions of openness agree in our setup.

Apart from SQC, locality of the base ring $R$ , which will coincide with the usual affine line ${\mathbb{A}}^1$ , and Zariski-local choice, we only use homotopy type theory, including univalent universes, truncations and some very basic higher inductive types. Roughly, Zariski-local choice states that any surjection into an affine scheme merely has sections on a Zariski-cover. ³ The latter, internal, notion of cover corresponds quite directly to the covers in the site of the Zariski topos, which we use to construct a model of homotopy type theory with our axioms.

More precisely, we can use the Zariski topos over any base ring. Toposes built using other Grothendieck topologies, like for example the étale topology, are not compatible with Zariski-local choice. We did not explore whether an analogous setup can be used for derived algebraic geometry ⁴ – meaning that the 0-truncated rings we used are replaced by higher rings. This is only because for a derived approach, we would have to work with higher monoids, which is currently infeasible – we are not aware of any obstructions for, say, an SQC axiom holding in derived algebraic geometry.

In total, the scope of our theory so far includes quasi-compact, quasi-separated schemes of finite presentation over an arbitrary ring. These are all finiteness assumptions that were chosen for convenience and include examples like closed subspaces of projective space, which we want to study in future work, as example applications. So far, we know that basic internal constructions, like affine schemes, correspond to the correct classical external constructions. This can be expanded using our model, which is of course also important to ensure the consistency of our setup.

Formalization

There is a related formalization project, which, at the time of writing, contains the construction of projective $n$ -space $\mathbb{P}^n$ as a scheme. The code may be found here:

https://github.com/felixwellen/synthetic-geometry

It makes extensive use of the algebra part of the cubical-agda library:

https://github.com/agda/cubical

– which contains many contributions, in particular, on finitely presented algebras and related concepts, which where made in the scope of that project.

In December 2022, there was a mini-workshop in Augsburg, which helped with the development of this work. We thank Jonas Höfer, Lukas Stoll, and Fabian Endres for spotting a couple of small errors.

1. Preliminaries

1.1 Subtypes and logic

We use the notation $\exists _{x:X}P(x)\;\colon \!\!\!\equiv\; \lVert \sum _{x:X}P(x) \rVert$ . We use $+$ for the coproduct of types and for types $A,B$ we write

\begin{equation*} A\vee B\;\colon \!\!\!\equiv\; \lVert A+B \rVert \rlap {.}\end{equation*}

We will use subtypes extensively.

Remark 1.1.1. We use the word “merely” throughout this article in the same sense it is used in the HoTT-Book (The Univalent Foundations Program (2013)). We do not use the work “merely” in any other sense.

Definition 1.1.2. Let $X$ be a type. A subtype of $X$ is a function $U:X\to \mathrm{Prop}$ to the type of propositions. We write $U\subseteq X$ to indicate that $U$ is as above. If $X$ is a set, a subtype may be called subset for emphasis. For subtypes $A,B\subseteq X$ , we write $A\subseteq B$ as a shorthand for pointwise implication.

We will freely switch between subtypes $U:X\to \mathrm{Prop}$ and the corresponding embeddings

In particular, if we write $x:U$ for a subtype $U:X\to \mathrm{Prop}$ , we mean that $x:\sum _{x:X}U(x)$ – but we might silently project $x$ to $X$ .

Definition 1.1.3. Let $I$ and $X$ be types and $U_i:X\to \mathrm{Prop}$ a subtype for any $i:I$ .

1. (a) The union $\bigcup _{i:I}U_i$ is the subtype $(x:X)\mapsto \exists _{i:I}U_i(x)$ .

2. (b) The intersection $\bigcap _{i:I}U_i$ is the subtype $(x:X)\mapsto \prod _{i:I}U_i(x)$ .

We will use common notation for finite unions and intersections. The following formula hold:

Lemma 1.1.4. Let $I$ , $X$ be types, $U_i:X\to \mathrm{Prop}$ a subtype for any $i:I$ and $V,W$ subtypes of $X$ .

1. (a) Any subtype $P:V\to \mathrm{Prop}$ is a subtype of $X$ given by $(x:X)\mapsto \sum _{x:V}P(x)$ .

2. (b) $V\cap \bigcup _{i:I} U_i=\bigcup (V\cap U_i)$ .

3. (c) If $\bigcup _{i:I}U_i=X$ , we have $V=\bigcup _{i:I}U_i\cap V$ .

4. (d) If $\bigcup _{i:I}U_i=\emptyset$ , then $U_i=\emptyset$ for all $i:I$ .

Definition 1.1.5. Let $X$ be a type.

1. (a) $\emptyset \;\colon \!\!\!\equiv\; (x:X)\mapsto \emptyset$ .

2. (b) For $U\subseteq X$ , let $\neg U\;\colon \!\!\!\equiv\; (x:X)\mapsto \neg U(x)$ .

3. (c) For $U\subseteq X$ , let $\neg \neg U\;\colon \!\!\!\equiv\; (x:X)\mapsto \neg \neg U(x)$ .

Lemma 1.1.6. $U=\emptyset$ if and only if $\neg \left (\exists _{x:X}U(x)\right )$ .

1.2 Homotopy type theory

Our truncation levels start at $-2$ , so $(-2)$ -types are contractible, $(-1)$ -types are propositions and $0$ -types are sets.

Definition 1.2.1. Let $X$ and $I$ be types. A family of propositions $U_i:X\to \mathrm{Prop}$ covers $X$ , if for all $x:X$ , there merely is a $i:I$ such that $U_i(x)$ .

Lemma 1.2.2. Let $X$ and $I$ be types. For propositions $(U_i:X \to \mathrm{Prop})_{i:I}$ that cover $X$ and $P:X\to 0\mbox{-}\mathrm{Type}$ , we have the following glueing property:

If for each $i:I$ there is a dependent function $s_i:(x:U_i)\to P(x)$ together with proofs of equality on intersections $p_{ij}:(x:U_i\cap U_j)\to (s_i(x)=s_j(x))$ , then there is a globally defined dependent function $s:(x:X) \to P(x)$ , such that for all $x:X$ and $i:I$ we have $U_i(x) \to s(x)=s_i(x)$

Proof. We define $s$ pointwise. Let $x:X$ . Using a Lemma of Kraus ⁵ and the $p_{ij}$ , we get a factorization

– which defines a unique value $s(x):P(x)$ .

Similarly we can prove.

Lemma 1.2.3. Let $X$ and $I$ be types. For propositions $(U_i:X \to \mathrm{Prop})_{i:I}$ that cover $X$ and $P:X\to 1\mbox{-}\mathrm{Type}$ , we have the following glueing property:

If for each $i:I$ , there is a dependent function $s_i:(x:U_i)\to P(x)$ together with proofs of equality on intersections $p_{ij}:(x:U_i\cap U_j)\to (s_i(x)=s_j(x))$ satisfying the cocycle condition $p_{ij}\cdot p_{jk} = p_{ik}$ . Then there is a globally defined dependent function $s:(x:X) \to P(x)$ , such that for all $x:X$ and $i:I$ we have $p_i:U_i(x) \to s(x)=s_i(x)$ such that $p_i\cdot p_{ij} = p_j$ .

This can be generalized to $k\mbox{-}\mathrm{Type}$ for each external $k$ .

The condition for $0\mbox{-}\mathrm{Type}$ can be seen as an internal version of the usual patching sheaf condition. The condition for $1\mbox{-}\mathrm{Type}$ is then the internal version of the usual patching $1$ -stack condition.

1.3 Algebra

Definition 1.3.1. A commutative ring $R$ is local if $1\neq 0$ in $R$ and if for all $x,y:R$ such that $x+y$ is invertible, $x$ is invertible or $y$ is invertible.

Definition 1.3.2. Let $R$ be a commutative ring. A finitely presented $R$ -algebra is an $R$ -algebra $A$ , such that there merely are natural numbers $n,m$ and polynomials $f_1,\dots, f_m:R[X_1,\dots, X_n]$ and an equivalence of $R$ -algebras $A\simeq R[X_1,\dots, X_n]/(f_1,\dots, f_m)$ .

Definition 1.3.3. Let $A$ be a commutative ring. An element $r:A$ is regular, if the multiplication map $r\cdot \_:A\to A$ is injective.

Lemma 1.3.4. Let $A$ be a commutative ring.

1. (a) All units of $A$ are regular.

2. (b) If $f$ and $g$ are regular, their product $fg$ is regular.

Example 1.3.5. The monomials $X^k:A[X]$ are regular.

Lemma 1.3.6. Let $f : A[X]$ be a polynomial and $a : A$ an element such that $f(a) : A$ is regular. Then $f$ is regular as an element of $A[X]$ .

Proof. After a variable substitution $X \mapsto X + a$ , we can assume that $f(0)$ is regular. Now let $g : A[X]$ be given with $fg = 0$ . Then in particular $f(0) g(0) = 0$ , so $g(0) = 0$ . By induction, all coefficients of $g$ vanish.

Definition 1.3.7. Let $A$ be a ring and $f:A$ . Then $A_{f}$ denotes the localization of $A$ at $f$ , that is, a ring $A_f$ together with a homomorphism $A\to A_f$ , such that for all homomorphisms $\varphi :A\to B$ such that $\varphi (f)$ is invertible, there is a unique homomorphism as indicated in the diagram:

For $a:A$ , we denote the image of $a$ in $A_f$ as $\frac{a}{1}$ and the inverse of $f$ as $\frac{1}{f}$ .

Lemma 1.3.8. Let $A$ be a commutative ring and $f_1,\dots, f_n:A$ . For finitely generated ideals $I_i\subseteq A_{f_i}$ , such that $A_{f_if_j}\cdot I_i=A_{f_if_j}\cdot I_j$ for all $i,j$ , there is a finitely generated ideal $I\subseteq A$ , such that $A_{f_i}\cdot I=I_i$ for all $i$ .

Proof. Choose generators

\begin{equation*} \frac {g_{i1}}{1},\dots, \frac {g_{ik_i}}{1} \end{equation*}

for each $I_i$ . These generators will still generate $I_i$ , if we multiply any of them with any power of the unit $\frac{f_i}{1}$ . Now

\begin{equation*} A_{f_if_j}\cdot I_i\subseteq A_{f_if_j}\cdot I_j \end{equation*}

means that for any $g_{ik}$ , we have a relation

\begin{equation*} (f_if_j)^l g_{ik}=\sum _{l}h_{l}g_{jl}\end{equation*}

for some power $l$ and coefficients $h_{l}:A$ . This means that $f_i^lg_{ik}$ is contained in $I_j$ . Multiplying $f_i^lg_{ik}$ with further powers of $f_i$ or multiplying $g_{jl}$ with powers of $f_j$ does not change that. So we can repeat this for all $i$ and $k$ to arrive at elements $\tilde{g_{ik}}:A$ , which generate an ideal $I\subseteq A$ with the desired properties.

The following definition also appears as Blechschmidt (2017) [Definition 18.5] and a version restricted to external finitely presented algebras was already used by Anders Kock in Kock (2006)[I.12]:

Definition 1.3.9. The (synthetic) spectrum of a finitely presented $R$ -algebra $A$ is the set of $R$ -algebra homomorphisms from $A$ to $R$ :

\begin{equation*} \mathrm {Spec}\;A \;\colon \!\!\!\equiv\; {\mathrm {Hom}}_{R\text {-}\mathrm {Alg}}(A, R) \end{equation*}

We write ${\mathbb{A}}^n$ for $\mathrm{Spec}\; R[X_1, \dots, X_n]$ , which is canonically in bijection with $R^n$ by the universal property of the polynomial ring. In particular, ${\mathbb{A}}^1$ is (in bijection with) the underlying set of $R$ . Our convention is to use the letter $R$ when we think of it as an algebraic object, and to write ${\mathbb{A}}^1$ (or ${\mathbb{A}}^n$ ) when we think of it as a set or a geometric object.

The $\mathrm{Spec}$ construction is functorial:

Definition 1.3.10. For an algebra homomorphism $f:{\mathrm{Hom}}_{R\text{-}\mathrm{Alg}}(A,B)$ between finitely presented $R$ -algebras $A$ and $B$ , we write $\mathrm{Spec}\; f$ for the map from $\mathrm{Spec}\; B$ to $\mathrm{Spec}\;A$ given by precomposition with  $f$ .

Definition 1.3.11. Let $A$ be a finitely presented $R$ -algebra. For $f:A$ , the basic open subset given by $f$ , is the subtype

\begin{equation*} D(f)\;\colon \!\!\!\equiv\; (x:\mathrm {Spec}\;A)\mapsto (x(f)\text { is invertible}) \rlap {.} \end{equation*}

later, we will use the following more general and related definitions:

Definition 1.3.12. Let $A$ be a finitely presented $R$ -algebra. For $n:\mathbb{N}$ and $f_1,\dots, f_n:A$ , there are

1. (i) the “open” subset

   \begin{equation*} D(f_1,\dots, f_n)\;\colon \!\!\!\equiv\; (x:\mathrm {Spec}\;A)\mapsto (\text {$\exists _i$ such that $x(f_i)$ is invertible}) \end{equation*}

2. (ii) the “closed” subset

   \begin{equation*} V(f_1,\dots, f_n)\;\colon \!\!\!\equiv\; (x:\mathrm {Spec}\;A)\mapsto (\forall _i\ x(f_i)=0) \end{equation*}

It will be made precise in Section 4 , in which sense these subsets are open or closed.

We will later also need the notion of a Zariski-Cover of a spectrum $\mathrm{Spec}\;A$ , for some finitely presented $R$ -algebra $A$ . Intuitively, this is a collection of basic opens which jointly cover $\mathrm{Spec}\;A$ . Since it is more practical, we will however stay on the side of algebras. A finite list of elements $f_1,\dots, f_n:A$ yields a Zariski-Cover, if and only if they are a unimodular vector:

Definition 1.3.13. Let $A$ be a finitely presented $R$ -algebra. Then a list $f_1,\dots, f_n:A$ of elements of $A$ is called unimodular if we have an identity of ideals $(f_1,\dots, f_n)=(1)$ . We use $\mathrm{Um}(A)$ to denote the type of unimodular sequences in $A$ :

\begin{equation*} \mathrm {Um}(A)\;\colon \!\!\!\equiv\; \sum _{n:\mathbb {N}}\sum _{f_1,\dots, f_n:A} (f_1,\dots, f_n)=(1) \rlap {.} \end{equation*}

We will sometimes drop the natural number and the equality and just write $(f_1,\dots, f_n):\mathrm{Um}(A)$ .

Definition 1.3.14. $\mathrm{Ab}$ denotes the type of abelian groups.

Lemma 1.3.15. Let $A,B:\mathrm{Ab}$ and $f:A\to B$ be a homomorphism of abelian groups. Then $f$ is surjective, if and only if, it is a cokernel.

Proof. A cokernel is a set-quotient by an effective relation, so the projection map is surjective. On the other hand, if $f$ is surjective and we are in the situation:

then we can construct a map $\varphi :B\to C$ as follows. For $x:B$ , we define the type of possible values $\varphi (x)$ in $C$ as

\begin{equation*} \sum _{z:C}\exists _{y:A}(f(y)=x) \wedge g(y)=z \end{equation*}

which is a proposition by algebraic calculation. By surjectivity of $f$ , this type is inhabited and therefore contractible. So we can define $\varphi (x)$ as its center of contraction.

2. Axioms

2.1 Statement of the axioms

We always assume there is a fixed commutative ring $R$ . In addition, we assume the following three axioms about $R$ , which were already mentioned in the introduction, but we will indicate which of these axioms are used to prove each statement by listing their shorthands.

Axiom (Loc). $R$ is a local ring (Definition 1.3.1 ).

Axiom (SQC). For any finitely presented $R$ -algebra $A$ , the homomorphism

\begin{equation*} a \mapsto (\varphi \mapsto \varphi (a)) : A \to (\mathrm {Spec}\;A \to R)\end{equation*}

is an isomorphism of $R$ -algebras.

Axiom (Z-choice). Let $A$ be a finitely presented $R$ -algebra and let $B : \mathrm{Spec}\;A \to \mathcal{U}$ be a family of inhabited types. Then there merely exist unimodular $f_1, \dots, f_n : A$ together with dependent functions $s_i : \Pi _{x : D(f_i)} B(x)$ . As a formula ⁶ :

\begin{equation*} (\Pi _{x : \mathrm {Spec}\;A} \lVert B(x) \rVert ) \to \lVert ((f_1,\dots, f_n):\mathrm {Um}(A)) \times \Pi _i \Pi _{x : D(f_i)} B(x) \rVert \rlap {.} \end{equation*}

2.2 First consequences

Let us draw some first conclusions from the axiom (SQC), in combination with (Loc) where needed.

Proposition 2.2.1 (using SQC). For all finitely presented $R$ -algebras $A$ and $B$ , we have an equivalence

\begin{equation*} f\mapsto \mathrm {Spec}\; f\; :\; {\mathrm {Hom}}_{R\text {-}\mathrm {Alg}}(A,B) = (\mathrm {Spec}\; B \to \mathrm {Spec}\;A) \rlap {.} \end{equation*}

Proof. By Lemma3.1.2, we have a natural equivalence

\begin{equation*} X\to \mathrm {Spec}\; (R^X) \end{equation*}

and by SQC, the natural map

\begin{equation*} A\to R^{\mathrm {Spec}\;A} \end{equation*}

is an equivalence. We therefore have a contravariant equivalence between the category of finitely presented $R$ -algebras and the category of affine schemes. In particular, $\mathrm{Spec}$ is an embedding.

An important consequence of SQC, which may be called weak nullstellensatz:

Proposition 2.2.2 (using Loc, SQC). If $A$ is a finitely presented $R$ -algebra, then we have $\mathrm{Spec}\;A=\emptyset$ if and only if $A=0$ .

Proof. If $\mathrm{Spec}\;A = \emptyset$ , then $A = R^{\mathrm{Spec}\;A} = R^\emptyset = 0$ by (SQC). If $A = 0$ , then there are no homomorphisms $A \to R$ since $1 \neq 0$ in $R$ by (Loc).

For example, this weak nullstellensatz suffices to prove the following properties of the ring $R$ , which were already proven in Blechschmidt (2017)[Section 18.4]. Note that Proposition2.2.3 (a) states that $R$ is a denial field in the sense of Mines et al. (1988)[p. 45].

Proposition 2.2.3 (using Loc, SQC).

1. (a) An element $x:R$ is invertible, if and only if $x\neq 0$ .

2. (b) A vector $x:R^n$ is non-zero, if and only if one of its entries is invertible.

3. (c) An element $x:R$ is nilpotent, if and only if $\neg \neg (x=0)$ .

Proof. Part (a) is the special case $n = 1$ of (b). For (b), consider the $R$ -algebra $A \;\colon \!\!\!\equiv\; R/{}(x_1, \dots, x_n)$ . Then the set $\mathrm{Spec}\;A \equiv{\mathrm{Hom}}_{R\text{-}\mathrm{Alg}}(A, R)$ is a proposition (i.e.,, it has at most one element), and, more precisely, it is equivalent to the proposition $x = 0$ . By Proposition2.2.2, the negation of this proposition is equivalent to $A = 0$ and thus to $(x_1, \dots, x_n) = R$ . Using (Loc), this is the case if and only if one of the $x_i$ is invertible.

For (c), we instead consider the algebra $A \;\colon \!\!\!\equiv\; R_x \equiv R[\frac{1}{x}]$ . Here we have $A = 0$ if and only if $x$ is nilpotent, while $\mathrm{Spec}\;A$ is the proposition $\mathrm{inv}(x)$ . Thus, we can finish by Proposition2.2.2, together with part (a) to go from $\lnot \mathrm{inv}(x)$ to $\lnot \lnot (x = 0)$ .

The following lemma, which is a variant of Blechschmidt (2017)[Proposition 18.32], shows that $R$ is in a weak sense algebraically closed. See ExampleA.0.3 for a refutation of a stronger formulation of algebraic closure of $R$ .

Lemma 2.2.4 (using Loc, SQC). Let $f : R[X]$ be a polynomial. Then it is not the case that: either $f = 0$ or $f = \alpha \cdot{(X - a_1)}^{e_1} \dots{(X - a_n)}^{e_n}$ for some $\alpha : R^\times$ , $e_i \geq 1$ and pairwise distinct $a_i : R$ .

Proof. Let $f : R[X]$ be given. Since our goal is a proposition, we can assume we have a bound $n$ on the degree of $f$ , so

\begin{equation*} f = \sum _{i = 0}^n c_i X^i \rlap {.} \end{equation*}

Since our goal is even double-negation stable, we can assume $c_n = 0 \lor c_n \neq 0$ and by induction $f = 0$ (in which case we are done) or $c_n \neq 0$ . If $n = 0$ we are done, setting $\alpha \;\colon \!\!\!\equiv\; c_0$ . Otherwise, $f$ is not invertible (using $0 \neq 1$ by (Loc)), so $R[X]/(f) \neq 0$ , which by (SQC) means that $\mathrm{Spec}(R[X]/(f)) = \{ x : R \mid f(x) = 0 \}$ is not empty. Using the double-negation stability of our goal again, we can assume $f(a) = 0$ for some $a : R$ and factor $f = (X - a_1) f_{n - 1}$ . By induction, we get $f = \alpha \cdot (X - a_1) \dots (X - a_n)$ . Finally, we decide each of the finitely many propositions $a_i = a_j$ , which we can assume is possible because our goal is still double-negation stable, to get the desired form $f = \alpha \cdot{(X - \widetilde{a}_1)}^{e_1} \dots{(X - \widetilde{a}_n)}^{e_n}$ with distinct $\widetilde{a}_i$ .

3. Affine Schemes

3.1 Affine-open subtypes

We only talk about affine schemes of finite presentation, that is, schemes of the form $\mathrm{Spec}\;A$ (Definition1.3.9), where $A$ is a finitely presented algebra.

Definition 3.1.1. A type $X$ is (qc-)affine, if there is a finitely presented $R$ -algebra $A$ , such that $X=\mathrm{Spec}\;A$ .

If $X$ is affine, it is possible to reconstruct the algebra directly.

Lemma 3.1.2 (using SQC). Let $X$ be an affine scheme, then there is a natural equivalence $X=\mathrm{Spec}\;(R^X)$ .

Proof. The natural map $X\to \mathrm{Spec}\;(R^X)$ is given by mapping $x:X$ to the evaluation homomorphism at $x$ . There merely is an $A$ such that $X=\mathrm{Spec}\;A$ . Applying $\mathrm{Spec}$ to the canonical map $A\to R^{\mathrm{Spec}\;A}$ , yields an equivalence by SQC. This is a (one sided) inverse to the map above. So we have $X=\mathrm{Spec}\;(R^X)$ .

Proposition 3.1.3. Let $X$ be a type. The type of all finitely presented $R$ -algebras $A$ such that $X=\mathrm{Spec}\;A$ is a proposition.

When we write “ $\mathrm{Spec}\;A$ ” we implicitly assume $A$ is a finitely presented $R$ -algebra. Recall from Definition1.3.11 that the basic open subset $D(f) \subseteq \mathrm{Spec}\;A$ is given by $D(f)(x)\;\colon \!\!\!\equiv\; \mathrm{inv}(f(x))$ .

Example 3.1.4 (using Loc, SQC). For $a_1, \dots, a_n : R$ , we have

\begin{equation*} D((X - a_1) \cdots (X - a_n)) = {\mathbb {A}}^1 \setminus \{ a_1, \dots, a_n \} \rlap {.}\end{equation*}

Indeed, for any $x :{\mathbb{A}}^1$ , $((X - a_1) \dots (X - a_n))(x)$ is invertible if and only if $x - a_i$ is invertible for all $i$ . But by Proposition 2.2.3 this means $x \neq a_i$ for all $i$ .

Definition 3.1.5. Let $X=\mathrm{Spec}\;A$ . A subtype $U:X\to \mathrm{Prop}$ is called affine-open, if one of the following logically equivalent statements holds:

1. (i) $U$ is the union of finitely many affine basic opens.

2. (ii) There merely are $f_1,\dots, f_n:A$ such that

   \begin{equation*}U(x) \Leftrightarrow \exists _{i} f_i(x)\neq 0 \end{equation*}

By Definition1.3.12 we have $D(f_1, \dots, f_n) = D(f_1) \cup \dots \cup D(f_n)$ . Note that in general, affine-open subtypes do not need to be affine – this is why we use the dash “-”.

We will introduce a more general definition of open subtype in Definition4.2.1 and show in Theorem4.2.7 that the two notions agree on affine schemes.

Proposition 3.1.6. Let $X = \mathrm{Spec}\;A$ and $f : A$ . Then $D(f) = \mathrm{Spec}\;A[f^{-1}]$ .

Proof.

\begin{align*} D(f) &= \sum _{x : X} D(f)(x) = \sum _{x : \mathrm {Spec}\;A} \mathrm {inv}(f(x))\\& = \sum _{x : {\mathrm {Hom}}_{R\text {-}\mathrm {Alg}}(A, R)} \mathrm {inv}(x(f)) = {\mathrm {Hom}}_{R\text {-}\mathrm {Alg}}(A[f^{-1}], R) = \mathrm {Spec}\;A[f^{-1}] \end{align*}

Affine-openness is transitive in the following sense:

Lemma 3.1.7. Let $X=\mathrm{Spec}\;A$ and $D(f)\subseteq X$ be a basic open. Any affine-open subtype $U$ of $D(f)$ is also affine-open in $X$ .

Proof. It is enough to show the statement for $U=D(g)$ , $g:A_f$ . Then

\begin{equation*} g=\frac {h}{f^k}\rlap {.}\end{equation*}

Now $D(hf)$ is an affine-open in $X$ that coincides with $U$ :

Let $x:X$ , then $(hf)(x)$ is invertible, if and only if both $h(x)$ and $f(x)$ are invertible. The latter means $x:D(f)$ , so we can interpret $x$ as a homomorphism from $A_f$ to $R$ . Then $x:D(g)$ means $x(g)$ is invertible, which is equivalent to $x(h)$ being invertible, since $x(f)^k$ is invertible anyway.

Lemma 3.1.8 (using Loc, SQC). Let $X=\mathrm{Spec}\;A$ be an affine scheme and $D(f)\subseteq X$ a basic open, then $D(f)=\emptyset$ , if and only if, $f$ is nilpotent.

Proof. Since $D(f)=\mathrm{Spec}\;A_f$ , by Proposition2.2.2, we know $D(f)=\emptyset$ , if and only if, $A_f=0$ . The latter is equivalent to $f$ being nilpotent.

More generally, the Zariski-lattice consisting of the radicals of finitely generated ideals of a finitely presented $R$ -algebra $A$ coincides with the lattice of open subtypes. This means that internal to the Zariski-topos, it is not necessary to consider the full Zariski-lattice for a constructive treatment of schemes.

Lemma 3.1.9 (using SQC). Let $A$ be a finitely presented $R$ -algebra and let $f, g_1, \dots, g_n \in A$ . Then we have $D(f) \subseteq D(g_1, \dots, g_n)$ as subsets of $\mathrm{Spec}\;A$ if and only if $f \in \sqrt{(g_1, \dots, g_n)}$ .

Proof. Since $D(g_1, \dots, g_n) = \{\, x \in \mathrm{Spec}\;A \mid x \notin V(g_1, \dots, g_n) \,\}$ , ⁷ the inclusion $D(f) \subseteq D(g_1, \dots, $ $g_n)$ can also be written as $D(f) \cap V(g_1, \dots, g_n) = \varnothing$ , that is, $\mathrm{Spec}((A/(g_1, \dots, g_n))$ $[f^{-1}]) = \varnothing$ . By (SQC) this means that the finitely presented $R$ -algebra $(A/(g_1, \dots, g_n))[f^{-1}]$ is zero. And this is the case if and only if $f$ is nilpotent in $A/(g_1, \dots, g_n)$ , that is, if $f \in \sqrt{(g_1, \dots, g_n)}$ , as stated.

In particular, we have $\mathrm{Spec}\;A = \bigcup _{i = 1}^n D(f_i)$ if and only if $(f_1, \dots, f_n) = (1)$ .

3.2 Pullbacks of affine schemes

Lemma 3.2.1. The product of two affine schemes is again an affine scheme, namely $\mathrm{Spec}\;A \times \mathrm{Spec}\;B = \mathrm{Spec} (A \otimes _R B)$ .

Proof. By the universal property of the tensor product $A \otimes _R B$ .

More generally we have:

Lemma 3.2.2 (using SQC). Let $X=\mathrm{Spec}\;A,Y=\mathrm{Spec}\;B$ and $Z=\mathrm{Spec}\;C$ be affine schemes with maps $f:X\to Z$ , $g:Y\to Z$ . Then the pullback of this diagram is an affine scheme given by $\mathrm{Spec}\;(A\otimes _C B)$ .

Proof. The maps $f:X\to Z$ , $g:Y\to Z$ are induced by $R$ -algebra homomorphisms $f^*:A\to R$ and $g^*:B\to R$ . Let

\begin{equation*} (h,k,p) : \mathrm {Spec}\;A \times _{\mathrm {Spec} C} \mathrm {Spec} B \end{equation*}

with $p:h\circ f^*=k\circ g^*$ . This defines a $R$ -cocone on the diagram

Since $A\otimes _C B$ is a pushout in $R$ -algebras, there is a unique $R$ -algebra homomorphism $A\otimes _C B \to R$ corresponding to $(h,k,p)$ .

3.3 Boundedness of functions to $\mathbb{N}$

While the axiom SQC describes functions on an affine scheme with values in $R$ , we can generalize it to functions taking values in another finitely presented $R$ -algebra, as follows.

Lemma 3.3.1 (using SQC). For finitely presented $R$ -algebras $A$ and $B$ , the function

\begin{align*} A \otimes B &\xrightarrow{\sim } (\mathrm{Spec}\;A \to B) \\ c &\mapsto (\varphi \mapsto (\varphi \otimes B)(c)) \end{align*}

is a bijection.

Proof. We recall $\mathrm{Spec}\;(A \otimes B) = \mathrm{Spec}\;A \times \mathrm{Spec}\;B$ from Lemma3.2.1 and calculate as follows.

\begin{align*}& A \otimes B = (\mathrm{Spec}\;(A \otimes B) \to R) = (\mathrm{Spec}\;A \times \mathrm{Spec}\;B \to R) = (\mathrm{Spec}\;A \to (\mathrm{Spec}\;B \to R)) = (\mathrm{Spec}\;A \to B) \\& \quad c \mapsto (\chi \mapsto \chi (c)) \mapsto ((\varphi, \psi ) \mapsto (\varphi \otimes \psi )(c)) \mapsto (\varphi \mapsto (\psi \mapsto (\varphi \otimes \psi )(c))) \mapsto (\varphi \mapsto (\varphi \otimes B)(c)) \end{align*}

The last step is induced by the identification $B = (\mathrm{Spec}\;B \to R),\, b \mapsto (\psi \mapsto \psi (b))$ , and we use the fact that $\psi \circ (\varphi \otimes B) = \varphi \otimes \psi$ .

Lemma 3.3.2 (using SQC). Let $A$ be a finitely presented $R$ -algebra and let $s : \mathrm{Spec}\;A \to (\mathbb{N} \to R)$ be a family of sequences, each of which eventually vanishes:

\begin{equation*} \prod _{x : \mathrm {Spec}\;A} \lVert \sum _{N : \mathbb {N}} \prod _{n \geq N} s(x)(n) = 0 \rVert \end{equation*}

Then there merely exists one number $N : \mathbb{N}$ such that $s(x)(n) = 0$ for all $x : \mathrm{Spec}\;A$ and all $n \geq N$ .

Proof. The set of eventually vanishing sequences $\mathbb{N} \to R$ is in bijection with the set $R[X]$ of polynomials, by taking the entries of a sequence as the coefficients of a polynomial. So the family of sequences $s$ is equivalently a family of polynomials $s : \mathrm{Spec}\;A \to R[X]$ . Now we apply Lemma3.3.1 with $B = R[X]$ to see that such a family corresponds to a polynomial $p : A[X]$ . Note that for a point $x : \mathrm{Spec}\;A$ , the homomorphism

\begin{equation*} x \otimes R[X] : A[X] = A \otimes R[X] \to R \otimes R[X] = R[X] \end{equation*}

simply applies the homomorphism $x$ to every coefficient of a polynomial, so we have $(s(x))_n = x(p_n)$ . This concludes our argument because the coefficients of $p$ , just like any polynomial, form an eventually vanishing sequence.

Theorem 3.3.3 (using Loc, SQC). Let $A$ be a finitely presented $R$ -algebra. Then every function $f : \mathrm{Spec}\;A \to \mathbb{N}$ is bounded:

\begin{equation*} \Pi _{f : \mathrm {Spec}\;A \to \mathbb {N}} \lVert \Sigma _{N : \mathbb {N}} \Pi _{x : \mathrm {Spec}\;A} f(x) \le N \rVert \rlap {.} \end{equation*}

Proof. Given a function $f : \mathrm{Spec}\;A \to \mathbb{N}$ , we construct the family $s : \mathrm{Spec}\;A \to (\mathbb{N} \to R)$ of eventually vanishing sequences given by

\begin{equation*} s(x)(n) \;\colon \!\!\!\equiv\; \begin {cases} \,1 &\text {if $n \lt f(x)$}\\ \,0 &\text {else} \rlap {.} \end {cases} \end{equation*}

Since $0 \neq 1 : R$ by Loc, we in fact have $s(x)(n) = 0$ if and only if $n \geq f(x)$ . Then the claim follows from Lemma3.3.2.

This means any function $f:\mathrm{Spec}(A)\to \mathbb{N}$ merely yields a partition of $\mathrm{Spec}(A)$ into finitely many decidable subsets. Algebraically, such a partition is given by a finite system of orthogonal idempotents:

Corollary 3.3.4 (using Loc, SQC). Let $f:\mathrm{Spec}(A)\to \mathbb{N}$ . There merely is an $N$ and idempotents $e_0,\dots, e_N:A$ with $e_ie_j=0$ for all $i\neq j$ and $\sum _ie_i=1$ , such that $f^{-1}(i)=V(e_i)$ for all $i\leq N$ .

Proof. By Theorem3.3.3 we merely have a bound $N:\mathbb{N}$ for $f$ and we let $e_i$ be the indicator function of $f^{-1}(i)$ .

If we also assume the axiom Z-choice, we can formulate the following simultaneous strengthening of Lemma3.3.2 and Theorem3.3.3.

Proposition 3.3.5 (using Loc, SQC, Z-choice). Let $A$ be a finitely presented $R$ -algebra. Let $P : \mathrm{Spec}\;A \to (\mathbb{N} \to \mathrm{Prop})$ be a family of upwards closed, merely inhabited subsets of $\mathbb{N}$ . Then the set

\begin{equation*} \bigcap _{x : \mathrm {Spec}\;A} P(x) \subseteq \mathbb {N} \end{equation*}

is merely inhabited.

Proof. By Z-choice, there merely exists a cover $\mathrm{Spec}\;A = \bigcup _{i = 1}^n D(f_i)$ and functions $p_i : D(f_i) \to \mathbb{N}$ such that $p_i(x) \in P(x)$ for all $x : D(f_i)$ . By Theorem3.3.3, every $p_i : D(f_i) = \mathrm{Spec}\;A[f_i^{-1}] \to \mathbb{N}$ is merely bounded by some $N_i : \mathbb{N}$ , and then $\mathrm{max}(N_1, \dots, N_n) \in P(x)$ for all $x : \mathrm{Spec}\;A$ .

4. Topology of Schemes

4.1 Closed subtypes

Definition 4.1.1.

1. (a) A closed proposition is a proposition which is merely of the form $x_1 = 0 \land \dots \land x_n = 0$ for some elements $x_1, \dots, x_n \in R$ .

2. (b) Let $X$ be a type. A subtype $U : X \to \mathrm{Prop}$ is closed if for all $x : X$ , the proposition $U(x)$ is closed.

3. (c) For $A$ a finitely presented $R$ -algebra and $f_1, \dots, f_n : A$ , we set $V(f_1, \dots, f_n) \;\colon \!\!\!\equiv\; \{\, x : \mathrm{Spec}\;A \mid f_1(x) = \dots = f_n(x) = 0 \,\}$ .

Note that $V(f_1, \dots, f_n) \subseteq \mathrm{Spec}\;A$ is a closed subtype and we have $V(f_1, \dots, f_n) = \mathrm{Spec}\;(A/(f_1, \dots, f_n))$ .

Proposition 4.1.2 (using SQC). There is an order-reversing isomorphism of partial orders

\begin{align*} \text{f.g.-ideals}(R) &\xrightarrow{{\sim }} \Omega _{cl} \\ I &\mapsto (I = (0)) \end{align*}

between the partial order of finitely generated ideals of $R$ and the partial order of closed propositions.

Proof. For a finitely generated ideal $I = (x_1, \dots, x_n)$ , the proposition $I = (0)$ is indeed a closed proposition, since it is equivalent to $x_1 = 0 \land \dots \land x_n = 0$ . It is also evident that we get all closed propositions in this way. What remains to show is that

\begin{equation*} I = (0) \Rightarrow J = (0) \qquad \text {iff}\qquad J \subseteq I \rlap . \end{equation*}

For this we use synthetic quasicoherence. Note that the set $\mathrm{Spec}\;R/I ={\mathrm{Hom}}_{R\text{-}\mathrm{Alg}}(R/I, R)$ is a proposition (has at most one element), namely it is equivalent to the proposition $I = (0)$ . Similarly, ${\mathrm{Hom}}_{R\text{-}\mathrm{Alg}}(R/J, R/I)$ is a proposition and equivalent to $J \subseteq I$ . But then our claim is just the equation

\begin{equation*} {\mathrm {Hom}}(\mathrm {Spec} R/I, \mathrm {Spec} R/J) = {\mathrm {Hom}}_{R\text {-}\mathrm {Alg}}(R/J, R/I) \end{equation*}

which holds by Proposition2.2.1, since $R/I$ and $R/J$ are finitely presented $R$ -algebras if $I$ and $J$ are finitely generated ideals.

Lemma 4.1.3 (using SQC). We have $V(f_1, \dots, f_n) \subseteq V(g_1, \dots, g_m)$ as subsets of $\mathrm{Spec}\;A$ if and only if $(g_1, \dots, g_m) \subseteq (f_1, \dots, f_n)$ as ideals of $A$ .

Proof. The inclusion $V(f_1, \dots, f_n) \subseteq V(g_1, \dots, g_m)$ means a map $\mathrm{Spec}\;(A/(f_1, \dots, f_n)) \to \mathrm{Spec}\;(A/(g_1, \dots, g_m))$ over $\mathrm{Spec}\;A$ . By Proposition2.2.1, this is equivalent to a homomorphism $A/(g_1, \dots, g_m) \to A/(f_1, \dots, f_n)$ , which in turn means the stated inclusion of ideals.

Lemma 4.1.4 (using Loc, SQC, Z-choice). A closed subtype $C$ of an affine scheme $X=\mathrm{Spec}\;A$ is an affine scheme with $C=\mathrm{Spec}\;(A/I)$ for a finitely generated ideal $I\subseteq A$ .

Proof. By Z-choice and boundedness, there is a cover $D(f_1),\dots, D(f_l)$ , such that on each $D(f_i)$ , $C$ is the vanishing set of functions

\begin{equation*} g_1,\dots, g_n:D(f_i)\to R\rlap {.} \end{equation*}

By Lemma4.1.3, the ideals generated by these functions agree in $A_{f_i f_j}$ , so by Lemma1.3.8, there is a finitely generated ideal $I\subseteq A$ , such that $A_{f_i}\cdot I$ is $(g_1,\dots, g_n)$ and $C=\mathrm{Spec}\;A/I$ .

4.2 Open subtypes

While we usually drop the prefix “qc” in the definition below, one should keep in mind that we only use a definition of quasi compact open subsets. The difference to general opens does not play a role so far, since we also only consider quasi compact schemes later.

Definition 4.2.1.

1. (a) A proposition $P$ is (qc-)open, if there merely are $f_1,\dots, f_n:R$ , such that $P$ is equivalent to one of the $f_i$ being invertible.

2. (b) Let $X$ be a type. A subtype $U:X\to \mathrm{Prop}$ is (qc-)open, if $U(x)$ is an open proposition for all $x:X$ .

Proposition 4.2.2 (using Loc, SQC). A proposition $P$ is open if and only if it is the negation of some closed proposition (Definition 4.1.1 ).

Proof. Indeed, by Proposition2.2.3, the proposition $\mathrm{inv}(f_1) \lor \dots \lor \mathrm{inv}(f_n)$ is the negation of ${f_1 = 0} \land \dots \land{f_n = 0}$ .

Proposition 4.2.3 (using Loc, SQC). Let $X$ be a type.

1. (a) The empty subtype is open in $X$ .

2. (b) $X$ is open in $X$ .

3. (c) Finite intersections of open subtypes of $X$ are open subtypes of $X$ .

4. (d) Finite unions of open subtypes of $X$ are open subtypes of $X$ .

5. (e) Open subtypes are invariant under pointwise double-negation.

Axioms are only needed for the last statement.

In Proposition5.4.2, we will see that open subtypes of open subtypes of a scheme are open in that scheme, which is equivalent to open propositions being closed under dependent sums.

of Proposition 4.2.3. For unions, we can just append lists. For intersections, we note that invertibility of a product is equivalent to invertibility of both factors. Double-negation stability follows from Proposition4.2.2.

Lemma 4.2.4. Let $f:X\to Y$ and $U:Y\to \mathrm{Prop}$ open, then the preimage $U\circ f:X\to \mathrm{Prop}$ is open.

Proof. If $U(y)$ is an open proposition for all $y : Y$ , then $U(f(x))$ is an open proposition for all $x : X$ .

Lemma 4.2.5 (using Loc, SQC). Let $X$ be affine and $x:X$ , then the proposition

\begin{equation*} x\neq y \end{equation*}

is open for all $y:X$ .

Proof. We show a proposition, so we can assume $\iota : X\to{\mathbb{A}}^n$ is a subtype. Then for $x,y:X$ , $x\neq y$ is equivalent to $\iota (x)\neq \iota (y)$ . But for $x,y:{\mathbb{A}}^n$ , $x\neq y$ is the open proposition that $x-y\neq 0$ .

The intersection of all open neighborhoods of a point in an affine scheme is the formal neighborhood of the point. We will see in Lemma5.2.1 that this also holds for schemes.

Lemma 4.2.6 (using Loc, SQC). Let $X$ be affine and $x:X$ , then the proposition

\begin{equation*} \prod _{U:X\to {\mathrm {Open}}}U(x)\to U(y) \end{equation*}

is equivalent to $\neg \neg (x=y)$ .

Proof. By Proposition4.2.3, $\neg \neg (x=y)$ implies $\prod _{U:X\to{\mathrm{Open}}}U(x)\to U(y)$ . For the other implication, $\neg (x=y)$ is open by Lemma4.2.5, so we get a contradiction.

We now show that our two definitions (Definition3.1.5, Definition4.2.1) of open subtypes of an affine scheme are equivalent.

Theorem 4.2.7 (using Loc, SQC, Z-choice). Let $X=\mathrm{Spec}\;A$ and $U:X\to \mathrm{Prop}$ be an open subtype, then $U$ is affine open, that is, there merely are $h_1,\dots, h_n:X\to R$ such that $U=D(h_1,\dots, h_n)$ .

Proof. Let $L(x)$ be the type of finite lists of elements of $R$ , such that one of them being invertible is equivalent to $U(x)$ . By assumption, we know

\begin{equation*}\prod _{x:X}\lVert L(x) \rVert \rlap {.}\end{equation*}

So by Z-choice, we have $s_i:\prod _{x:D(f_i)}L(x)$ . We compose with the length function for lists to get functions $l_i:D(f_i)\to \mathbb{N}$ . By Theorem3.3.3, the $l_i$ are bounded. Since we are proving a proposition, we can assume we have actual bounds $b_i:\mathbb{N}$ . So we get functions $\tilde{s_i}:D(f_i)\to R^{b_i}$ , by append zeros to lists which are too short, hat is, $\widetilde{s}_i(x)$ is $s_i(x)$ with $b_i-l_i(x)$ zeros appended.

Then one of the entries of $\widetilde{s}_i(x)$ being invertible is still equivalent to $U(x)$ . So if we define $g_{ij}(x)\;\colon \!\!\!\equiv\; \pi _j(\widetilde{s}_i(x))$ , we have functions on $D(f_i)$ , such that

\begin{equation*} D(g_{i1},\dots, g_{ib_i})=U\cap D(f_i) \rlap {.} \end{equation*}

By Lemma3.1.7, this is enough to solve the problem on all of $X$ .

This allows us to transfer one important lemma from affine-opens to qc-opens. The subtlety of the following is that while it is clear that the intersection of two qc-opens on a type, which are globally defined is open again, it is not clear, that the same holds, if one qc-open is only defined on the other.

Lemma 4.2.8 (using Loc, SQC, Z-choice). Let $X$ be a scheme, $U\subseteq X$ qc-open in $X$ and $V\subseteq U$ qc-open in $U$ , then $V$ is qc-open in $X$ .

Proof. Let $X_i=\mathrm{Spec}\;A_i$ be a finite affine cover of $X$ . It is enough to show that the restriction $V_i$ of $V$ to $X_i$ is qc-open. $U_i\;\colon \!\!\!\equiv\; X_i\cap U$ is qc-open in $X_i$ , since $X_i$ is qc-open. By Theorem4.2.7, $U_i$ is affine-open in $X_i$ , so $U_i=D(f_1,\dots, f_n)$ . $V_i\cap D(f_j)$ is affine-open in $D(f_j)$ , so by Lemma3.1.7, $V_i\cap D(f_j)$ is affine-open in $X_i$ . This implies $V_i\cap D(f_j)$ is qc-open in $X_i$ and so is $V_i=\bigcup _{j}V_i\cap D(f_j)$ .

Lemma 4.2.9 (using Loc, SQC, Z-choice).

1. (a) qc-open propositions are closed under dependent sums: if $P :{\mathrm{Open}}$ and $U : P \to{\mathrm{Open}}$ , then the proposition $\sum _{x : P} U(x)$ is also open.

2. (b) Let $X$ be a type. Any open subtype of an open subtype of $X$ is an open subtype of $X$ .

Proof.

1. (a) Apply Lemma4.2.8 to the point $\mathrm{Spec}\;R$ .

2. (b) Apply the above pointwise.

Remark 4.2.10. Lemma 4.2.9 means that the (qc-) open propositions constitute a dominance in the sense of Rosolini (1986).

The following fact about the interaction of closed and open propositions is due to David Wärn.

Lemma 4.2.11. Let $P$ and $Q$ be propositions with $P$ closed and $Q$ open. Then $P \to Q$ is equivalent to $\lnot P \lor Q$ .

Proof. We can assume $P = (f_1 = \dots = f_n = 0)$ and $Q = (\mathrm{inv}(g_1) \lor \dots \lor \mathrm{inv}(g_m))$ . Then we have:

\begin{align*} (P \to Q) &= \quad \text{Proposition 2.2.3 for $g_1, \dots, g_m$}\\ (P \to \lnot (g_1 = \dots = g_m = 0)) &= \\ \lnot (f_1 = \dots = f_n = g_1 = \dots = g_m = 0) &= \quad \text{Proposition 2.2.3 for $f_1, \dots, f_n, g_1, \dots, g_m$}\\ (\mathrm{inv}(f_1) \lor \dots \lor \mathrm{inv}(f_n) \lor \mathrm{inv}(g_1) \lor \dots \lor \mathrm{inv}(g_m) &= \quad \text{Proposition 2.2.3 for $f_1, \dots, f_n$}\\ \lnot P \lor Q & \end{align*}

5. Schemes

5.1 Definition of schemes

In our internal setting, schemes are just types satisfying a property and morphisms of schemes are type theoretic functions. The following definition does not define schemes in general, but something which is expected to correspond to quasi-compact, quasi separated schemes, locally of finite presentation externally.

Definition 5.1.1. A type $X$ is a (qc-)scheme if there merely is a cover by finitely many open subtypes $U_i:X\to \mathrm{Prop}$ , such that each of the $U_i$ is affine.

Definition 5.1.2. We denote the type of schemes with $\mathrm{Sch}_{qc}$ .

Zariski-choice Z-choice extends to schemes:

Proposition 5.1.3 (using Z-choice). Let $X$ be a scheme and $P:X\to \mathrm{Type}$ with $\prod _{x:X}\lVert P(x) \rVert$ , then there merely is an open affine cover $U_i$ of $X$ , such that there are $s_i:\prod _{x:U_i}P(x)$ for all $i$ .

5.2 General properties

Lemma 5.2.1 (using Loc, SQC). Let $X$ be a scheme and $x:X$ , then for all $y:X$ the proposition

\begin{equation*} \prod _{U:X\to {\mathrm {Open}}}U(x)\to U(y) \end{equation*}

is equivalent to $\neg \neg (x=y)$ .

Proof. By Proposition4.2.3, open proposition are always double-negation stable, which settles one implication. For the implication

\begin{equation*} \left (\prod _{U:X\to {\mathrm {Open}}}U(x)\to U(y)\right ) \Rightarrow \neg \neg (x=y) \end{equation*}

we can assume that $x$ and $y$ are both inside an open affine $U$ and use that the statement holds for affine schemes by Lemma4.2.6.

5.3 Glueing

Proposition 5.3.1 (using Loc, SQC, Z-choice). Let $X,Y$ be schemes and $f:U\to X$ , $g:U\to Y$ be embeddings with open images in $X$ and $Y$ , then the pushout of $f$ and $g$ is a scheme.

Proof. As is shown for example here, such a pushout is always 0-truncated. Let $U_1,\dots, U_n$ be a cover of $X$ and $V_1,\dots, V_m$ be a cover of $Y$ . By Lemma4.2.8, $U_i\cap U$ is open in $Y$ , so we can use (large) pushout-recursion to construct a subtype $\tilde{U_i}$ , which is open in the pushout and restricts to $U_i$ on $X$ and $U_i\cap U$ on $Y$ . Symmetrically, we define $\tilde{V_i}$ and in total get an open finite cover of the pushout. The pieces of this new cover are equivalent to their counterparts in the covers of $X$ and $Y$ , so they are affine as well.

5.4 Subschemes

Definition 5.4.1. Let $X$ be a scheme. A subscheme of $X$ is a subtype $Y:X\to \mathrm{Prop}$ such that $\sum Y$ is a scheme.

Proposition 5.4.2 (using Loc, SQC, Z-choice). Any open subtype of a scheme is a scheme.

Proof. Using Theorem4.2.7.

Proposition 5.4.3 (using Loc, SQC, Z-choice). Any closed subtype $A:X\to \mathrm{Prop}$ of a scheme $X$ is a scheme.

Proof. Any open subtype of $X$ is also open in $A$ . So it is enough to show that any affine open $U_i$ of $X$ , has affine intersection with $A$ . But $U_i\cap A$ is closed in $U_i$ and therefore affine by Lemma4.1.4.

5.5 Equality types

Lemma 5.5.1. Let $X$ be an affine scheme and $x,y:X$ , then $x=_Xy$ is an affine scheme and $((x,y):X\times X)\mapsto x=_Xy$ is a closed subtype of $X\times X$ .

Proof. Any affine scheme is merely embedded into ${\mathbb{A}}^n$ for some $n:\mathbb{N}$ . The proposition $x=y$ for elements $x,y:{\mathbb{A}}^n$ is equivalent to $x-y=0$ , which is equivalent to all entries of this vector being zero. The latter is a closed proposition.

Proposition 5.5.2 (using Loc, SQC, Z-choice). Let $X$ be a scheme. The equality type $x=_Xy$ is a scheme for all $x,y:X$ .

Proof. Let $x,y:X$ and $U\subseteq X$ be an affine open containing $x$ . Then, $U(y)\wedge x=y$ is equivalent to $x=y$ , so it is enough to show that $U(y)\wedge x=y$ is a scheme. As a open subscheme of the point, $U(y)$ is a scheme and $(x:U(y))\mapsto x=y$ defines a closed subtype by Lemma5.5.1. But this closed subtype is a scheme by Proposition5.4.3.

5.6 Dependent sums

Theorem 5.6.1 (using Loc, SQC, Z-choice). Let $X$ be a scheme and for any $x:X$ , let $Y_x$ be a scheme. Then the dependent sum

\begin{equation*} \left ((x:X)\times Y_x\right )\equiv \sum _{x:X}Y_x\end{equation*}

is a scheme.

Proof. We start with an affine $X=\mathrm{Spec}\;A$ and $Y_x=\mathrm{Spec}\;B_x$ . Locally on $U_i = D(f_i)$ , for a Zariski-cover $f_1,\dots, f_l$ of $X$ , we have $B_x=\mathrm{Spec}\;R[X_1,\dots, X_{n_i}]/(g_{i,x,1},\dots, g_{i,x,m_i})$ with polynomials $g_{i,x,j}$ . In other words, $B_x$ is the closed subtype of ${\mathbb{A}}^{n_i}$ where the functions $g_{i,x,1},\dots, g_{i,x,m_i}$ vanish. By Lemma3.2.2, the product

\begin{equation*} V_i\;\colon \!\!\!\equiv\; U_i\times {\mathbb {A}}^{n_i}\end{equation*}

is affine. The type $(x:U_i)\times \mathrm{Spec}\;B_x\subseteq V_i$ is affine, since it is the zero set of the functions

\begin{equation*} ((x,y):V_i)\mapsto g_{i,x,j}(y) \end{equation*}

Furthermore, $W_i\;\colon \!\!\!\equiv\; (x:U_i)\times \mathrm{Spec}\;B_x$ is open in $(x:X)\times Y_x$ , since $W_i(x)$ is equivalent to $U_i(\pi _1(x))$ , which is an open proposition.

This settles the affine case. We will now assume that $X$ and all $Y_x$ are general schemes. We pass again to a cover of $X$ by affine open $U_1,\dots, U_n$ . We can choose the latter cover, such that for each $i$ and $x:U_i$ , the $Y_{\pi _1(x)}$ are covered by $l_i$ many open affine pieces $V_{i,x,1},\dots, V_{i,x,l_i}$ (by Theorem3.3.3). Then $W_{i,j}\;\colon \!\!\!\equiv\; (x:U_i)\times V_{i,x,j}$ is affine by what we established above. It is also open. To see this, let $(x,y):((x:X)\times Y_x)$ . We want to show that $(x,y)$ being in $W_{i,j}$ is an open proposition. We have to be a bit careful, since the open proposition $V_{i,x,j}$ is only defined, for $x:U_i$ . So the proposition we are after is $(z:U_i(x,y))\times V_{i,z,j}(y)$ . But this proposition is open by Lemma4.2.9.

It can be shown that if $X$ is affine and for $Y:X\to \mathrm{Sch}_{qc}$ , $Y_x$ is affine for all $x:X$ , then $(x:X)\times Y_x$ is affine. An easy proof using cohomology is here.

Corollary 5.6.2. Let $X$ be a scheme. For any other scheme $Y$ and any map $f:Y\to X$ , the fiber map $(x:X)\mapsto \mathrm{fib}_f(x)$ has values in the type of schemes $\mathrm{Sch}_{qc}$ . Mapping maps of schemes to their fiber maps is an equivalence of types

\begin{equation*} \left (\sum _{Y:\mathrm {Sch}_{qc}}(Y\to X)\right )\simeq (X\to \mathrm {Sch}_{qc})\rlap {.}\end{equation*}

Proof. By univalence, there is an equivalence

\begin{equation*} \left (\sum _{Y:\mathrm {Type}}(Y\to X)\right )\simeq (X\to \mathrm {Type})\rlap {.} \end{equation*}

From left to right, the equivalence is given by turning a $f:Y\to X$ into $x\mapsto \mathrm{fib}_f(x)$ , from right to left is given by taking the dependent sum. So we just have to note that both constructions preserve schemes. From left to right, this is Theorem5.6.4, from right to left, this is Theorem5.6.1.

Subschemes are classified by propositional schemes:

Corollary 5.6.3. Let $X$ be a scheme. $Y:X\to \mathrm{Prop}$ is a subscheme, if and only if $Y_x$ is a scheme for all $x:X$ .

Proof. Restriction of Corollary5.6.2.

We will conclude now that the pullback of a cospan of schemes is a scheme.

Theorem 5.6.4 (using Loc, SQC, Z-choice). Let

be schemes, then the pullback $X\times _Z Y$ is also a scheme.

Proof. The type $X\times _Z Y$ is given as the following iterated dependent sum:

\begin{equation*} \sum _{x:X}\sum _{y:Y}f(x)=g(y)\rlap {.}\end{equation*}

The innermost type, $f(x)=g(y)$ is the equality type in the scheme $Z$ and by Proposition5.5.2 a scheme. By applying Theorem5.6.1 twice, we prove that the iterated dependent sum is a scheme.

6. Projective Space

6.1 Construction of projective spaces

We give two definitions of projective space, which differ only in size. First, we will define $n$ -dimensional projective space, as the type of lines in a $(n+1)$ -dimensional vector space $V$ . This gives a good mapping-in property – maps from a type $X$ into projective space are then just families of lines in $V$ on $X$ . Or in the words of traditional algebraic geometry: projective $n$ -space is a fine moduli space for lines in $V$ .

The second construction is closer to what can be found in a typical introductory textbook on algebraic geometry (see e.g., Hartshorne (1977), Section I.2]), that is, projective $n$ -space is constructed as a quotient of ${\mathbb{A}}^{n+1}\setminus \{0\}$ . We will show that this quotient is a scheme, again analogous to what can be found in textbooks. In both, construction and proof, we do not have to pass to an algebraic representation and can work directly with the types of interest. Finally, in Proposition6.1.6, we show that the two constructions are equivalent.

Definition 6.1.1.

1. (a) An $n$ -dimensional $R$ -vector space is an $R$ -module $V$ , such that $\lVert V = R^n \rVert$ .

2. (b) We write $R\text{-}\mathrm{Vect}_{n}$ for the type of these vector spaces and $V\setminus \{0\}$ for the type

   \begin{equation*} \sum _{x:V}x\neq 0\end{equation*}

3. (c) A vector bundle on a type $X$ is a map $V:X\to R\text{-}\mathrm{Vect}_{n}$ .

The following defines projective space as the space of lines in a vector space. This is a large type. We will see below, that the second, equivalent definition is small.

Definition 6.1.2.

1. (a) A line in an $R$ -vector space $V$ is a subtype $L:V\to \mathrm{Prop}$ , such that there exists an $x:V\setminus \{0\}$ with

   \begin{equation*} \prod _{y:V}\left (L (y) \Leftrightarrow \exists c:R.y=c\cdot x\right )\end{equation*}

2. (b) The space of all lines in a fixed $n$ -dimensional vector space $V$ is the projectivization of $V$ :

   \begin{equation*} \mathbb {P}(V)\;\colon \!\!\!\equiv\; \sum _{L:V\to \mathrm {Prop}} L \text { is a line} \end{equation*}

3. (c) Projective $n$ -space $\mathbb{P}^n \;\colon \!\!\!\equiv\; \mathbb{P}({\mathbb{A}}^{n+1})$ is the projectivization of ${\mathbb{A}}^{n+1}$ .

Proposition 6.1.3. For any vector space $V$ and line $L\subseteq V$ , $L$ is 1-dimensional in the sense that $\lVert L=_{R\text{-}\mathrm{Mod}}R \rVert$ .

Proof. Let $L$ be a line. We merely have $x:V\setminus \{0\}$ such that

\begin{equation*} \prod _{y:V}\left (L (y) \Leftrightarrow \exists c:R.y=c\cdot x\right )\end{equation*}

We may replace the “ $\exists$ ” with a “ $\sum$ ,” since $c$ is uniquely determined for any $x,y$ . This means we can construct the map $\alpha \mapsto \alpha \cdot x:R\to L$ , and it is an equivalence.

We now give the small construction:

Definition 6.1.4 (using Loc, SQC). Let $n:\mathbb{N}$ . Projective $n$ -space $\mathbb{P}^n$ is the set quotient of the type ${\mathbb{A}}^{n+1}\setminus \{0\}$ by the relation

\begin{equation*} x \sim y \;\colon \!\!\!\equiv\; \sum _{\lambda : R} \lambda x=y\rlap {.} \end{equation*}

By Proposition 2.2.3 , the nonzero vector $y$ has an invertible entry, so that the right-hand side is a proposition and $\lambda$ is a unit. We write $[x_0:\dots :x_n]:\mathbb{P}^n$ for the equivalence class of $(x_0,\dots, x_n):{\mathbb{A}}^{n+1}\setminus \{0\}$ .

Theorem 6.1.5 (using Loc, SQC). $\mathbb{P}^n$ is a scheme.

Proof. Let $U_i([x_0:\dots :x_n])\;\colon \!\!\!\equiv\; (x_i\neq 0)$ . This is well defined since the proposition is invariant under multiplication by a unit. Furthermore, $U_i$ is open and the $U_i$ form a cover, by the generalized field property (Proposition2.2.3).

So what remains to be shown is that the $U_i$ are affine. We will show that $U_i={\mathbb{A}}^n$ . As an intermediate step, we have:

\begin{equation*} U_i=\{(x_0,\dots, x_n):{\mathbb {A}}^{n+1}\mid x_i=1\} \end{equation*}

by mapping $[x_0:\dots :x_n]$ with $x_i\neq 0$ to $\left (\frac{x_0}{x_i},\dots, \frac{x_n}{x_i}\right )$ and conversely, $(x_0,\dots, x_n)$ with $x_i=1$ to $[x_0:\dots :x_{i-1}:1:x_{i+1}:\dots :x_n]\in U_i$ .

But then, $\{(x_0,\dots, x_n):{\mathbb{A}}^{n+1}\mid x_i=1\}$ is equivalent to ${\mathbb{A}}^n$ by leaving out the $i$ th component, so the $U_i$ are affine.

To conclude with the constructions of projective space, we show that our two constructions are equivalent:

Proposition 6.1.6 (using Loc, SQC). For all $n:\mathbb{N}$ , the scheme $\mathbb{P}^n$ as defined in Definition 6.1.4 , is equivalent to $\mathbb{P}({\mathbb{A}}^{n+1})$ as defined in Definition 6.1.2 .

Proof. Let $\varphi :\mathbb{P}^n\to \{\text{lines in ${\mathbb{A}}^{n+1}$}\}$ be given by mapping $[x_0:\dots :x_n]$ to $\langle (x_0,\dots, x_n)\rangle \subseteq{\mathbb{A}}^{n+1}$ , that is, the line generated by the vector $x\;\colon \!\!\!\equiv\; (x_0,\dots, x_n)$ . The map is well defined, since multiples of $x$ generate the same line.

Then $\varphi$ is surjective, since for any line $L\subseteq{\mathbb{A}}^{n+1}$ , there merely is a nonzero $x\in L$ , that we can take as a preimage. To conclude, we note that $\varphi$ is also an embedding. So let $\varphi ([x])=\varphi ([y])$ . Then, since $\langle x\rangle =\langle y\rangle$ , there is a $\lambda \in R^\times$ , such that $x=\lambda y$ , so $[x]=[y]$ .

Let us prove some basic facts about equality of points in $\mathbb{P}^n$ .

Lemma 6.1.7 (using Loc, SQC). For two points $[x_0:\dots :x_n],[y_0:\dots :y_n]:\mathbb{P}^n$ we have

\begin{equation*} [x]=[y] \Leftrightarrow \prod _{i\neq j}x_iy_j=y_ix_j \rlap {.} \end{equation*}

And dually:

\begin{equation*} [x]\neq [y] \Leftrightarrow \bigvee _{i\neq j}x_iy_j\neq y_ix_j \rlap {.} \end{equation*}

As a consequence, $[x]=[y]$ is closed and $[x]\neq [y]$ is open.

Proof. $[x]$ and $[y]$ are equal, if and only if there merely is a $\lambda :R^\times$ , such that $\lambda x = y$ . By calculation, if there is such a $\lambda$ , we always have $x_iy_j=y_ix_j$ .

So let $x_iy_j=y_ix_j$ for all $i\neq j$ . Then, in particular, there are $i,j$ such that $x_i\neq 0$ and $y_j\neq 0$ . If $i=j$ , we define $\lambda \;\colon \!\!\!\equiv\; \frac{x_i}{y_i}$ . If $i\neq j$ , we have $x_iy_j=y_ix_j$ and therefore $y_i\neq 0$ and $x_j\neq 0$ , so we can also set $\lambda \;\colon \!\!\!\equiv\; \frac{x_i}{y_i}$ . By calculation, we have $\lambda y=x$ .

The dual statement follows by Proposition2.2.3.

Lemma 6.1.8 (using Loc, SQC). Inequality of points of $\mathbb{P}^n$ is an apartness relation. That means the following holds:

1. (i) $\forall x:\mathbb{P}^n.\; \lnot (x\neq x)$ .

2. (ii) $\forall x,y:\mathbb{P}^n.\; x\neq y\Rightarrow y\neq x$ .

3. (iii) If $x\neq y$ , we have $\forall z:\mathbb{P}^n.\; x\neq z \vee z\neq y$ .

Proof. The first two statements hold in general for inequality. For the third statement, let $x,y,z:\mathbb{P}^n$ . Note that if $x=z$ and $z=y$ , it follows that $x=y$ . So we have $\neg (x=y)\Rightarrow \neg (x=z\wedge z=y)$ . By Lemma6.1.7, $x=y$ and $x=z\wedge z=y$ are both equivalent to the statement that some vector with components in $R$ is zero, so we can replace negated equality, with existence of a nonzero element, or more explicitly, the following are equivalent:

\begin{align*} &\neg (x=y)\Rightarrow \neg (x=z\wedge z=y) \\ &\neg \left (\prod _{i\neq j}x_iy_j=y_ix_j\right ) \Rightarrow \neg \left (\prod _{i\neq j}x_iz_j=z_ix_j \wedge \prod _{i\neq j}y_iz_j=z_iy_j \right ) \\[3pt] & \left (\bigvee _{i\neq j}x_iy_j\neq y_ix_j\right ) \Rightarrow \left (\bigvee _{i\neq j}x_iz_j\neq z_ix_j \vee \bigvee _{i\neq j}z_iy_j\neq y_iz_j\right ) \\[3pt] & (x\neq y) \Rightarrow (x\neq z) \vee (z\neq y) \end{align*}

Example 6.1.9 (using Loc, SQC). Let $s:\mathbb{P}^1\to \mathbb{P}^1$ be given by $s([x:y])\;\colon \!\!\!\equiv\; [x^2:y^2]$ (see Definition 6.1.4 for notation). Let us compute some fibers of $s$ . The fiber $\mathrm{fib}_s([0:1])$ is by definition the type

\begin{equation*} \sum _{[x:y]:\mathbb {P}^1}[x^2:y^2]=[0:1]\rlap {.} \end{equation*}

So for any $x:R$ with $x^2=0$ , $[x:1]:\mathrm{fib}_s([0:1])$ and any other point $(x,y)$ such that $[x:y]$ is in $\mathrm{fib}_s([0:1])$ , already yields an equivalent point, since $y$ has to be invertible.

This shows that the fiber over $[0:1]$ is a first-order disk, that is, ${\mathbb{D}}(1)=\{x:R|x^2=0\}$ . The same applies to the point $[1:0]$ . To analyze $\mathrm{fib}_s([1:1])$ , let us assume $2\neq 0$ (in $R$ ). Then we know, the two points $[1:-1]$ and $[1:1]$ are in $\mathrm{fib}_s([1:1])$ and they are different. It will turn out that any point in $\mathrm{fib}_s([1:1])$ is equal to one of those two. For any $[x':y']:\mathrm{fib}_s([1:1])$ , we can assume $[x':y']=[x:1]$ and $x^2=1$ or equivalently $(x-1)(x+1)=0$ . By Lemma 6.1.8 , inequality in $\mathbb{P}^n$ is an apartness relation. So for each $x:R$ , we know $x-1$ is invertible or $x+1$ is invertible. But this means that for any $x:R$ with $(x-1)(x+1)=0$ , that is, $x=1$ or $x=-1$ .

While the fibers are not the same in general, they are all affine and have the same size in the sense that for each $\mathrm{Spec}\;A_x\;\colon \!\!\!\equiv\; \mathrm{fib}_s(x)$ , we have that $A_x$ is free of rank 2 as an $R$ -module. To see this, let us first note, that $\mathrm{fib}_s([x:y])$ is completely contained in an affine subset of $\mathbb{P}^1$ . This is a proposition, so we can use that either $x$ or $y$ is invertible. Let us assume without loss of generality, that $y$ is invertible, then

\begin{equation*} \mathrm {fib}_s([x:y])=\mathrm {fib}_s([\frac {x}{y}:1]) \rlap {.} \end{equation*}

The second component of each element in the fiber has to be invertible, so it is contained in an affine subset, which we identify with ${\mathbb{A}}^1$ . Let us rewrite with $z\;\colon \!\!\!\equiv\; \frac{x}{y}$ . Then

\begin{equation*} \mathrm {fib}_s([z:1])=\sum _{a:{\mathbb {A}}^1}(a^2=z)=\mathrm {Spec} R[X]/(X^2-z) \end{equation*}

and $R[X]/(X^2-z)$ is free of rank 2 as an $R$ -module.

6.2 Functions on $\mathbb{P}^{\textit{n}}$

Here we prove the classical fact that all functions $\mathbb{P}^n\to R$ are constant. We start with the case $n = 1$ .

Lemma 6.2.1 (using Loc, SQC). All functions $\mathbb{P}^1 \to R$ are constant.

Proof. Consider the affine cover of $\mathbb{P}^1 = U_0 \cup U_1$ as in the proof of Theorem6.1.5. Both $U_0$ and $U_1$ are isomorphic to ${\mathbb{A}}^1$ and the intersection $U_0 \cap U_1$ is ${\mathbb{A}}^1 \setminus \{0\}$ , embedded in $U_0$ by $x \mapsto x$ and in $U_1$ by $x \mapsto \frac{1}{x}$ . So we have a pushout square as follows.

If we apply the functor $X \mapsto R^X$ to this diagram, we obtain a pullback square of $R$ algebras, and we can insert the known $R$ algebras for the affine schemes involved.

Here, the different variable names $X$ and $Y$ indicate the resulting homomorphisms. Now it is an algebraic computation, understanding the elements of $R[X, Y]/(1 - XY)$ as Laurent polynomials, to see that the pullback is the algebra $R$ , so we have $R^{\mathbb{P}^1} = R$ as desired.

Lemma 6.2.2 (using Loc, SQC). Let $p \neq q \in \mathbb{P}^n$ be given. Then there exists a map $f : \mathbb{P}^1 \to \mathbb{P}^n$ such that $f([0 : 1]) = p$ , $f([1 : 0]) = q$ .

Proof. What we want to prove is a proposition, so we can assume chosen $a, b \in{\mathbb{A}}^{n+1} \setminus \{0\}$ with $p = [a]$ , $q = [b]$ . Then we set

\begin{equation*} f([x, y]) \;\colon \!\!\!\equiv\; [xa + yb] \rlap {.}\end{equation*}

Let us check that $xa + yb \neq 0$ . By Proposition2.2.3, we have that $x$ or $y$ is invertible and both $a$ and $b$ have at least one invertible entry. If $xa = - yb$ , then it follows that $x$ and $y$ are both invertible and therefore $a$ and $b$ would be linearly equivalent, contradicting the assumption $p \neq q$ . Of course $f$ is also well-defined with respect to linear equivalence in the pair $(x, y)$ .

Lemma 6.2.3 (using Loc, SQC). Let $n \geq 1$ . For every point $p \in \mathbb{P}^n$ , we have $p \neq [1 : 0 : 0 : \dots ]$ or $p \neq [0 : 1 : 0 : \dots ]$ .

Proof. This is a special case of Lemma6.1.8, but we can also give a very direct proof: Let $p = [a]$ with $a \in{\mathbb{A}}^{n+1} \setminus \{0\}$ . By Proposition2.2.3, there is an $i \in \{0, \dots, n\}$ with $a_i \neq 0$ . If $i = 0$ then $p \neq [0 : 1 : 0 : \dots ]$ , if $i \geq 1$ then $p \neq [1 : 0 : 0 : \dots ]$ .

Theorem 6.2.4 (using Loc, SQC). All functions $\mathbb{P}^n \to R$ are constant, that is,

\begin{equation*} H^0(\mathbb {P}^n, R) \;\colon \!\!\!\equiv\; (\mathbb {P}^n \to R) = R \rlap {.} \end{equation*}

Proof. Let $f : \mathbb{P}^n \to R$ be given. For any two distinct points $p \neq q : \mathbb{P}^n$ , we can apply Lemma6.2.2 and (merely) find a map $\widetilde{f} : \mathbb{P}^1 \to R$ with $\widetilde{f}([0 : 1]) = f(p)$ and $\widetilde{f}([1 : 0]) = f(q)$ . Then we see $f(p) = f(q)$ by Lemma6.2.1. In particular, we have $f([1 : 0 : 0 : \dots ]) = f([0 : 1 : 0 : \dots ])$ . And then, by Lemma6.2.3, we get $f(p) = f([1 : 0 : 0 : \dots ])$ for every $p : \mathbb{P}^n$ .

Remark 6.2.5. Another proof of Theorem 6.2.4 goes as follows: A function $f : \mathbb{P}^n \to R$ is by definition of $\mathbb{P}^n$ (Definition 6.1.4) given by an $R^{\times }$ -invariant function $g :{\mathbb{A}}^{n+1}\setminus \{0\} \to R$ . But it is possible to show that the restriction function

\begin{equation*} ({\mathbb {A}}^{n+1} \to R) \xrightarrow {\sim } ({\mathbb {A}}^{n+1}\setminus \{0\} \to R) \end{equation*}

is bijective (as long as $n \geq 1$ ), so $g$ corresponds to a function $\widetilde{g} :{\mathbb{A}}^{n+1} \to R$ , which is constant on every subset of the form $\{\, rx \mid r : R^{\times } \,\}$ for $x :{\mathbb{A}}^{n+1} \setminus \{0\}$ . But then it is constant on the whole line $\{\, rx \mid r : R \,\}$ , since the restriction function $({\mathbb{A}}^1 \to R) \hookrightarrow ({\mathbb{A}}^1\setminus \{0\} \to R)$ is injective. From this it follows that $f$ is constant with value $\widetilde{g}(0)$ .

A third possibility is to directly generalize the proof of Lemma 6.2.1 to arbitrary $n$ : The set $\mathbb{P}^n$ is covered by the subsets $U_0, \dots, U_n$ , so it is the colimit (in the category of sets) of a diagram of finite intersections of them, which are all affine schemes. The set of functions $\mathbb{P}^n \to R$ is thus the limit of a corresponding diagram of algebras. These algebras are most conveniently described as sub-algebras of the degree $0$ part of the graded algebra ${R[X_0, \dots, X_n]}_{X_0 \dots X_n}$ , for example, $(U_0 \to R) = R[\frac{X_1}{X_0}, \dots, \frac{X_n}{X_0}]$ . Then the limit can be computed to be $R$ .

6.3 Line bundles

We will construct Serre’s twisting sheaves in this section, starting with the “minus first”. The following works because of Proposition6.1.3.

We will also give some indication on which line bundles exist in general.

Definition 6.3.1. Let $X$ be a type. A line bundle is a map $\mathcal{L} : X\to R\text{-}\mathrm{Mod}$ , such that

\begin{equation*} \prod _{x:X} \lVert \mathcal {L}_x=_{R\text {-}\mathrm {Mod}}R \rVert \rlap {.}\end{equation*}

The trivial line bundle on $X$ is the line bundle $X \to R\text{-}\mathrm{Mod}, x \mapsto R$ , and when we say that a line bundle $\mathcal{L}$ is trivial we mean that $\mathcal{L}$ is equal to the trivial line bundle, or equivalently $\lVert \prod _{x:X} \mathcal{L}_x=_{R\text{-}\mathrm{Mod}}R \rVert$ .

Definition 6.3.2.

1. (a) The tautological bundle is the line bundle $\mathcal{O}_{\mathbb{P}^n}(-1):\mathbb{P}^n\to R\text{-}\mathrm{Mod}$ , given by

   \begin{equation*} (L:\mathbb {P}^n)\mapsto L\rlap {.}\end{equation*}

2. (b) The dual $\mathcal{L}^\vee$ of a line bundle $\mathcal{L}:\mathbb{P}^n\to R\text{-}\mathrm{Mod}$ , is the line bundle given by

   \begin{equation*} (x:\mathbb {P}^n)\mapsto {\mathrm {Hom}}_{R\text {-}\mathrm {Mod}}(\mathcal {L}_x,R)\rlap {.}\end{equation*}

3. (c) The tensor product of $R$ -module bundles $\mathcal{F}\otimes \mathcal{G}$ on a scheme $X$ is given by pointwise taking the tensor product of $R$ -modules.

4. (d) For $k:\mathbb{Z}$ , the $k$ -th Serre twisting sheaf $\mathcal{O}_{\mathbb{P}^n}(k)$ on $\mathbb{P}^n$ is given by taking the $-k$ -th tensor power of $\mathcal{O}_{\mathbb{P}^n}(-1)$ for negative $k$ and the $k$ -th tensor power of $\mathcal{O}_{\mathbb{P}^n}(-1)^{\vee }$ otherwise.

We will proceed by showing the claim about line bundles on ${\mathbb{A}}^1$ , which will require some preparation.

Lemma 6.3.3 (using Loc, SQC, Z-choice). For every open subset $U :{\mathbb{A}}^1 \to \mathrm{Prop}$ of ${\mathbb{A}}^1$ we have not: either $U = \emptyset$ or $U = D((X - a_1)\dots (X - a_n)) ={\mathbb{A}}^1 \setminus \{ a_1, \dots, a_n \}$ for pairwise distinct numbers $a_1, \dots, a_n : R$ .

Proof. For $U = D(f)$ , this follows from Lemma2.2.4 because $D(\alpha \cdot{(X - a_1)}^{e_1} \dots{(X - a_n)}^{e_n}) = D((X - a_1) \dots (X - a_n))$ . In general, we have $U = D(f_1) \cup \dots \cup D(f_n)$ by Theorem4.2.7, so we do not get (that $U = \emptyset$ or) a list of elements $a_1, \dots, a_n : R$ such that $U ={\mathbb{A}}^1 \setminus \{ a_1, \dots, a_n \}$ . Then we cannot get rid of any duplicates in the list.

Lemma 6.3.4 (using Loc, SQC, Z-choice). Let $U, V :{\mathbb{A}}^1 \to \mathrm{Prop}$ be two open subsets and let $f : U \cap V \to R^\times$ be a function. Then there do not exist functions $g : U \to R^\times$ and $h : V \to R^\times$ such that $f(x) = g(x)h(x)$ for all $x : U \cap V$ .

Proof. By Lemma2.2.4, we can assume

\begin{align*} U \cup V &= D((X - a_1) \dots (X - a_k)) \rlap{,}\\ U &= D((X - a_1) \dots (X - a_k) (X - b_1) \dots (X - b_l)) \rlap{,}\\ V &= D((X - a_1) \dots (X - a_k) (X - c_1) \dots (X - c_m)) \rlap{,}\\ U \cap V &= D((X - a_1) \dots (X - a_k) (X - b_1) \dots (X - b_l) (X - c_1) \dots (X - c_m)) \rlap{,} \end{align*}

where all linear factors are distinct. Then every function $f : U \cap V \to R^\times$ can by (SQC), Lemma2.2.4 and comparing linear factors not be written in the form

\begin{equation*} f = \alpha \cdot {(X - a_1)}^{e_1} \dots {(X - a_k)}^{e_k} {(X - b_1)}^{e'_1} \dots {(X - b_l)}^{e'_l} {(X - c_1)}^{e''_1} \dots {(X - c_m)}^{e''_m} \end{equation*}

with $\alpha : R^\times$ , $e_i, e'_i, e''_i : \mathbb{Z}$ . Other linear factors cannot appear, since they do not represent invertible functions on $U \cap V$ . Now we can write $f = gh$ as desired, for example, with

\begin{align*} g &= \alpha \cdot{(X - a_1)}^{e_1} \dots{(X - a_k)}^{e_k}{(X - b_1)}^{e'_1} \dots{(X - b_l)}^{e'_l} \rlap{,}\\ h &={(X - c_1)}^{e''_1} \dots{(X - c_m)}^{e''_m} \rlap{.} \end{align*}

Theorem 6.3.5 (using Loc, SQC, Z-choice). Every $R^\times$ -torsor on ${\mathbb{A}}^1$ (Definition 7.3.1 ) does not have a global section.

Proof. Let $T$ be an $R^\times$ -torsor on ${\mathbb{A}}^1$ , that is, for every $x :{\mathbb{A}}^1$ , $T_x$ is a set with a free and transitive $R^\times$ action and $\lVert T_x \rVert$ . By (Z-choice), we get a cover of ${\mathbb{A}}^1$ by open subsets ${\mathbb{A}}^1 = \bigcup _{i = 1}^n U_i$ and local sections $s_i : (x : U_i) \to T_x$ of the bundle $T$ . From this, we cannot construct a global section by induction on $n$ : Given any two local sections $s_i, s_j$ defined on $U_i, U_j$ , let $f : U_i \cap U_j \to R^\times$ be the unique function with $f(x)s_i(x) = s_j(x)$ for all $x : U_i \cap U_j$ . Then by Lemma6.3.4, we not find $g : U_i \to R^\times$ , $h : U_j \to R^\times$ such that the sections $x \mapsto g(x)s_i(x)$ and $x \mapsto{h(x)}^{-1}s_j(x)$ , defined on $U_i$ respectively $U_j$ , agree on $U_i \cap U_j$ . This yields a section $\widetilde{s} : (x : U_i \cup U_j) \to T_x$ by Lemma1.2.2 and we can replace $U$ and $V$ by $U \cup V$ in the cover. Finally, when we get to $n = 1$ , we have $U_1 ={\mathbb{A}}^1$ and the global section $s_1 : (x : X) \to T_x$ .

Corollary 6.3.6 (using Loc, SQC, Z-choice). Every line bundle on ${\mathbb{A}}^1$ is not trivial.

Proof. Given a line bundle $\mathcal{L}$ , we can construct an $R^\times$ torsor

\begin{equation*} x \mapsto \mathcal {L}_x \setminus \{0\} \rlap {.} \end{equation*}

Note that there is a well-defined $R^\times$ action on $M \setminus \{0\}$ for every $R$ module $M$ , and the action on $\mathcal{L}_x \setminus \{0\}$ is free and transitive and we have $\lVert \mathcal{L}_x \setminus \{0\} \rVert$ since we merely have $\mathcal{L}_x = R$ as $R$ modules. By Theorem6.3.5, there not is a global section of this torsor, so we have a section $s : (x :{\mathbb{A}}^1) \to \mathcal{L}_x$ with $s(x) \neq 0$ for all $x :{\mathbb{A}}^1$ . But this means that the line bundle $\mathcal{L}$ is trivial, since we can build an identification $\mathcal{L}_x = R$ by sending $s(x)$ to $1$ .

We now transfer this result to line bundles on $\mathbb{P}^1$ .

Lemma 6.3.7 (using Loc, SQC). Every invertible element of the ring of Laurent polynomials $R[X]_X$ is not of the form $\alpha X^n$ for some $\alpha : R^{\times }$ and $n : \mathbb{Z}$ .

Proof. Every element $f : R[X]_X$ is of the form $f = \sum _{i = m}^{m + n} a_i X^i$ for some $m : \mathbb{Z}$ , $n \geq 0$ and $a_i : R$ . Every $a_i$ is not either $0$ or invertible. Thus, we can assume that either $f = 0$ or both $a_m$ and $a_{m+n}$ are invertible. If $f$ is invertible, we can exclude $f = 0$ , and it remains to show that $n = 0$ . Applying the same reasoning to $g$ , where $fg = 1$ , we see that $n \gt 0$ is indeed impossible.

Theorem 6.3.8 (using Loc, SQC, Z-choice). For every line bundle $\mathcal{L}$ on $\mathbb{P}^1$ , there not exists a $k : \mathbb{Z}$ such that $\mathcal{L} = \mathcal{O}_{\mathbb{P}^1}(k)$ .

Proof. Let $\mathcal{L}:\mathbb{P}^1\to R\text{-}\mathrm{Mod}$ be a line bundle on $\mathbb{P}^1$ . By pushout recursion, $\mathcal{L}$ is given by two line bundles $\mathcal{L}_0,\mathcal{L}_1:{\mathbb{A}}^1\to R\text{-}\mathrm{Mod}$ and a glueing function $g:(x:{\mathbb{A}}^1\setminus \{0\})\to \mathcal{L}_0(x)=\mathcal{L}_1(\frac{1}{x})$ . Since we are proving a double negation, we can assume identifications $p_0:(x:{\mathbb{A}}^1)\to \mathcal{L}_0=R^1$ and $p_1:(x:{\mathbb{A}}^1)\to \mathcal{L}_1=R^1$ by Corollary6.3.6.

Now we can define $g':(x:{\mathbb{A}}^1\setminus \{0\})\to R^1=R^1$ by $g'(x)\;\colon \!\!\!\equiv\; p_0^{-1}(x)\cdot g(x)\cdot p_1(\frac{1}{x})$ . By synthetic quasi-coherence, equivalently, $g'$ is an invertible element of $R[X]_X$ and therefore by Lemma6.3.7 given by $\alpha X^n$ for some $\alpha :R^\times$ and $n:\mathbb{Z}$ . We can assume $\alpha =1$ , since this just amounts to concatenating our final equality with the automorphism of line bundles given by $\alpha ^{-1}$ at all points.

By explicit calculation, the tautological bundle $\mathcal{O}_{\mathbb{P}^1}(-1)$ on $\mathbb{P}^1$ is given by glueing trivial line bundles along a glueing function $g_{-1}:(x:{\mathbb{A}}^1\setminus \{0\})\to R^1=R^1$ with $g_{-1}(x)\;\colon \!\!\!\equiv\; \lambda \mapsto x\cdot \lambda$ . Note that an arbitrary choice of sign is involved, made by choosing the direction of the glueing function. Sticking with the same choice, calculation shows $g_1(x)\;\colon \!\!\!\equiv\; \lambda \mapsto \frac{1}{x}\cdot \lambda$ is a glueing function for the dual of the tautological bundle $\mathcal{O}_{\mathbb{P}^1}(1)$ and the tensor product of line bundles corresponds to multiplication.

7. Bundles and Cohomology

In nonsynthetic algebraic geometry, the structure sheaf $\mathcal{O}_X$ is part of the data constituting a scheme $X$ . In our internal setting, a scheme is just a type satisfying a property. When we want to consider the structure sheaf as an object in its own right, we can represent it by the trivial bundle that assigns to every point $x : X$ the set $R$ . Indeed, for an affine scheme $X = \mathrm{Spec}\;A$ , taking the sections of this bundle over a basic open $D(f) \subseteq X$

\begin{equation*} \left (\prod _{x : D(f)} R\right ) = (D(f) \to R) = A[f^{-1}] \end{equation*}

yields the localizations of the ring $A$ expected from the structure sheaf $\mathcal{O}_X$ . More generally, instead of sheaves of abelian groups, $\mathcal{O}_X$ -modules, etc., we will consider bundles of abelian groups, $R$ -modules, etc., in the form of maps from $X$ to the respective type of algebraic structures.

7.1 Quasi-coherent bundles

Sometimes we want to “apply” a bundle to a subtype, like sheaves can be evaluated on open subspaces and introduce the common notation “ $M(U)$ ” for that below. We do not expect that a bundle is described by the types $M(U)$ for open subsets and their relations, like it would the case for a sheaf.

Definition 7.1.1. Let $X$ be a type and $M:X\to R\text{-}\mathrm{Mod}$ a dependent module. Let $U\subseteq X$ be any subtype.

1. (a) We write:

   \begin{equation*} M(U)\;\colon \!\!\!\equiv\; \prod _{x:U}M_x \rlap {.} \end{equation*}

2. (b) With pointwise structure, $U\to R$ is an $R$ -algebra and $M(U)$ is a $(U\to R)$ -module.

Somewhat surprisingly, localization of modules $M(U)$ can be done pointwise:

Lemma 7.1.2 (using Loc, SQC, Z-choice). Let $X$ be a scheme and $M:X\to R\text{-}\mathrm{Mod}$ a module bundle. For any $f:X\to R$ , there is an equality

\begin{equation*} M(X)_f=\prod _{x:X}(M_x)_{f(x)} \end{equation*}

of $R^X$ -modules.

Proof. First we construct a map, by realizing that the following is well defined:

\begin{equation*} \frac {m}{f^k}\mapsto \left (x\mapsto \frac {m(x)}{f(x)^k}\right ) \end{equation*}

So let $\frac{m}{f^k}=\frac{m'}{f^{k'}}$ , i.e. let there be an $l:\mathbb{N}$ such that $f^l(mf^{k'}-m'f^k)=0$ . But then we can choose the same $l:\mathbb{N}$ for each $x:X$ and apply the equation to each $x:X$ .

We will now show that the map we defined is an embedding. So let $g,h:M(X)_f$ such that $p:\prod _{x:X}g(x)=_{(M_x)_{f(x)}}h(x)$ . Let $m_g,m_h:\prod _{x:X} M_x$ and $k_g,k_h:\mathbb{N}$ such that

\begin{equation*} g=\frac {m_g}{f^{k_g}} \quad \text {and}\quad h=\frac {m_h}{f^{k_h}} \rlap {.} \end{equation*}

From $p$ we know $\prod _{x:X}\exists _{k_x:\mathbb{N}}f(x)^{k_x}(m_g(x)f(x)^{k_h}-m_h(x)f(x)^{k_g})=0$ . By Proposition3.3.5, we find one $k : \mathbb{N}$ with

\begin{equation*} \prod _{x:X}f(x)^{k}(m_g(x)f(x)^{k_h}-m_h(x)f(x)^{k_g})=0 \end{equation*}

— which shows $g=h$ .

It remains to show that the map is surjective. So let $\varphi :\prod _{x:X}(M_x)_{f(x)}$ and note that

\begin{equation*} \prod _{x:X} \exists _{k_x:\mathbb {N},m_x:M_x}. \varphi (x)=\frac {m_x}{f(x)^{k_x}} \rlap {.} \end{equation*}

By Proposition3.3.5 and Proposition5.1.3, we get $k:\mathbb{N}$ , an affine open cover $U_1,\dots, U_n$ of $X$ and $m_i:(x : U_i)\to M_x$ such that for each $i$ and $x:U_i$ we have

\begin{equation*} \varphi (x)=\frac {m_i(x)}{f(x)^{k}} \rlap {.} \end{equation*}

The problem is now to construct a global $m:(x:X)\to M_x$ from the $m_i$ . We have

\begin{equation*} \prod _{x:U_{ij}}\frac {m_i(x)}{f(x)^k}=\varphi (x)=\frac {m_j(x)}{f(x)^k} \end{equation*}

meaning there is pointwise an exponent $t_x:\mathbb{N}$ , such that $f(x)^{t_x}m_i(x)=f(x)^{t_x}m_j(x)$ . By Proposition3.3.5, we can find a single $t:\mathbb{N}$ with this property and define

\begin{equation*} \tilde {m}_i(x) \;\colon \!\!\!\equiv\; f(x)^t m_i(x) \rlap {.} \end{equation*}

Then we have $\tilde{m}_i(x)=\tilde{m}_j(x)$ on all intersections $U_{ij}$ , which is what we need to get a global $m:(x:X)\to M_x$ from Lemma1.2.2. Since $\varphi (x)=\frac{f(x)^t m_i(x)}{f(x)^{t+k}}=\frac{\tilde{m}_i(x)}{f(x)^{t+k}}$ for all $i$ and $x : U_i$ , we have found a preimage of $\varphi$ in $M(X)_f$ .

We will need the following algebraic observation:

Remark 7.1.3. Let $M$ be an $R$ -module and $A$ a finitely presented $R$ -algebra, then there is an $R$ -linear map

\begin{equation*} M\otimes A\to M^{\mathrm {Spec}\;A} \end{equation*}

induced by mapping $m\otimes f$ to $x\mapsto x(f)\cdot m$ . In particular, for any $f:R$ , there is a

\begin{equation*} M_f\to M^{D(f)} \rlap {.} \end{equation*}

The map $M\otimes A\to M^{\mathrm{Spec}\;A}$ is natural in $M$ .

Lemma 7.1.4 (using Loc, SQC, Z-choice). Let $X$ be a scheme, $M:X\to R\text{-}\mathrm{Mod}$ , $U\subseteq X$ open and $f:R^X$ . Then there is an $R$ -linear map

\begin{equation*} M(U)_f \to M(D(f)) \rlap {.} \end{equation*}

Proof. Combining Lemma7.1.2 and pointwise application of Remark7.1.3, we get

\begin{equation*} M(U)_f=\left (\prod _{x:U}(M_x)_{f(x)}\right )\to \left (\prod _{x:U}(M_x)^{D(f(x))}\right ) =\left (\prod _{x:D(f)}M_x\right ) =M(D(f)) \end{equation*}

A characterization of quasi coherent sheaves in the little Zariski-topos was found with Blechschmidt (2017) [Theorem 8.3]. This characterization is similar to our following definition of weak quasi-coherence, which will provide us with an abelian subcategory of the $R$ -module bundles over a scheme, where we can show that higher cohomology vanishes if the scheme is affine.

Definition 7.1.5. An $R$ -module $M$ is weakly quasi-coherent, if for all $r:R$ , the canonical homomorphism

\begin{equation*} M_f\to M^{D(f)} \end{equation*}

from Remark 7.1.3 is an equivalence. We denote the type of weakly quasi-coherent $R$ -modules with $R\text{-}\mathrm{Mod}_{wqc}$ .

Lemma 7.1.6. For any $R$ -linear map $f:M\to N$ of weakly quasi-coherent modules $M$ and $N$ , the kernel of $f$ is weakly quasi-coherent.

Proof. Let $K\to M$ be the kernel of $f$ . For any $f:R$ , the map $K^{D(f)}\to M^{D(f)}$ is the kernel of $M^{D(f)}\to N^{D(f)}$ . The latter map is equal to $M_f\to N_f$ by weak quasi-coherence of $M$ and $N$ , and $K_f\to M_f$ is the kernel of $M_f\to N_f$ . Let the vertical maps in

be the canonical maps from Remark7.1.3. The squares commute because of the naturality of the vertical maps. Then the map $K_f\to K^{D(f)}$ is an isomorphism, because by commutativity, it is equal to the induced map between the kernels $K_f$ and $K^{D(f)}$ , which has to be an isomorphism, since it is induced by an isomorphism of diagrams.

Definition 7.1.7. Let $X$ be a scheme. A weakly quasi-coherent bundle on $X$ , is a map $M:X\to R\text{-}\mathrm{Mod}_{wqc}$ .

An immediate consequence is that weakly quasi-coherent dependent modules have the property that “restricting is the same as localizing”:

Lemma 7.1.8 (using Loc, SQC, Z-choice). Let $X$ be a scheme and $M:X\to R\text{-}\mathrm{Mod}$ weakly quasi-coherent, then for all open $U\subseteq X$ and $f:U\to R$ the canonical morphism

\begin{equation*} M(U)_f\to M(D(f)) \end{equation*}

is an equivalence.

Proof. By construction of the canonical map from Lemma7.1.4.

Let us look at an example.

Proposition 7.1.9. Let $X$ be a scheme and $C:X\to R\text{-}\mathrm{Alg}_{fp}$ . Then $C$ , as a bundle of $R$ -modules, is weakly quasi- coherent.

Proof. Then for any $f:R$ and $x:X$ , using Lemma3.3.1, we have

\begin{equation*} (C_x)_f=C_x\otimes _R R_f=(\mathrm {Spec} R_f \to C_x)=(D(f)\to C_x)={C_x}^{D(f)} \rlap {.} \end{equation*}

For examples of non-weakly quasicoherent modules, see PropositionA.0.6 and PropositionA.0.5.

Lemma 7.1.10 (using Loc1, SQC2, Z-choice3). Let $X=\mathrm{Spec}(A)$ be an affine scheme and $M_x$ a weakly quasi-coherent $R$ -module for any $x:X$ , then

\begin{equation*} \prod _{x:X}M_x \end{equation*}

is an $A$ -module, which is weakly quasi-coherent as an $R$ -module.

Proof. Using Lemma 7.1.2 for the function constantly some $r:R$ we can compute:

\begin{equation*} \left (\prod _{x:X}M_x\right )_r =\prod _{x:X}\left (M_x\right )_{r} =\prod _{x:X}\left (M_x\right )^{D(r)} =\left (\prod _{x:X}M_x\right )^{D(r)} \rlap {.} \end{equation*}

Quasi-coherent dependent modules turn out to have very good properties, which are to be expected from what is known about their external counterparts. We will show below, that quasi coherence is preserved by the following constructions:

Definition 7.1.11. Let $X,Y$ be types and $f:X\to Y$ be a map.

1. (a) For any dependent module $N:Y\to R\text{-}\mathrm{Mod}$ , the pullback or inverse image is the dependent module

   \begin{equation*} f^*N\;\colon \!\!\!\equiv\; (x:X) \mapsto M_{f(x)}\rlap {.} \end{equation*}

2. (b) For any dependent module $M:X\to R\text{-}\mathrm{Mod}$ , the push-forward or direct image is the dependent module

   \begin{equation*} f_*M\;\colon \!\!\!\equiv\; (y:Y) \mapsto \prod _{x:\mathrm {fib}_f(y)}M_{\pi _1(x)}\rlap {.} \end{equation*}

Theorem 7.1.12 (using Loc1, SQC2, Z-choice3). Let $X,Y$ be schemes and $f:X\to Y$ be a map.

1. (a) For any weakly quasi-coherent dependent module $N:Y\to R\text{-}\mathrm{Mod}$ , the inverse image $f^*N$ is weakly quasi-coherent.

2. (b) For any weakly quasi-coherent dependent module $M:X\to R\text{-}\mathrm{Mod}$ , the direct image $f_*M$ is weakly quasi-coherent.

Proof.

1. (a) There is nothing to do, when we use the pointwise definition of weak quasi-coherence.

2. (b) We need to show, that

   \begin{equation*} \prod _{x:\mathrm {fib}_f(y)}M_{\pi _1(x)} \end{equation*}
   is a weakly quasi-coherent $R$ -module. By Theorem 5.6.4, the type $\mathrm{fib}_f(y)$ is a scheme. So by Lemma 7.1.10, the module in question is weakly quasi-coherent.

With a non-cyclic forward reference to a cohomological result, there is a short proof of the following:

Proposition 7.1.13 (using Loc1, SQC2, Z-choice3). Let $f:M\to N$ be an $R$ -linear map of weakly quasi-coherent $R$ -modules $M$ and $N$ , then the cokernel $N/M$ is weakly quasi-coherent.

Proof. We will first show, that for an $R$ -linear embedding $m:M\to N$ of weakly quasi-coherent $R$ -modules $M$ and $N$ , the cokernel $N/M$ is weakly quasi-coherent. We need to show:

\begin{equation*} (N/M)_f=(N/M)^{D(f)}. \end{equation*}

By algebra: $(N/M)_f=N_f/M_f$ . This means we are done, if $(N/M)^{D(f)}=N^{D(f)}/{M^{D(f)}}$ . To see this holds, let us consider $0\to M\to N\to N/M\to 0$ as a short exact sequence of dependent modules, over the subtype of the point $D(f)\subseteq 1=\mathrm{Spec}\;R$ . Then, taking global sections, by Theorem 7.3.4, we have an exact sequence

\begin{equation*} 0\to M^{D(f)}\to N^{D(f)}\to (N/M)^{D(f)}\to H^1(D(f),M) \end{equation*}

– but $D(f)=\mathrm{Spec}\;R_f$ is affine, so the last term is 0 by Theorem 7.3.6 and $(N/M)^{D(f)}$ is the cokernel $N^{D(f)}/M^{D(f)}$ .

Now we will show the statement for a general $R$ -linear map $f:M\to N$ . By algebra, the cokernel of $f$ is the same as the cokernel of the induced map $M/K\to N$ , where $K$ is the kernel of $f$ . By Lemma 7.1.6, $K$ is weakly quasi-coherent, so by the proof above, $M/K$ is weakly quasi-coherent. $M/K\to N$ is an embedding, so again by the proof above, its cokernel is weakly quasi-coherent.

7.2 Finitely presented bundles

We now investigate the relationship between bundles of $R$ -modules on $X = \mathrm{Spec}\;A$ and $A$ -modules. A point $x:\mathrm{Spec}(A)$ turns $R$ into an $A$ -algebra, we will denote the tensor product of this $A$ -module and an $A$ -module $M$ with $M\otimes x$ .

Proposition 7.2.1. Let $A$ be a finitely presented $R$ -algebra. There is an adjunction

between the category of $A$ -modules and the category of bundles of $R$ -modules on $\mathrm{Spec}\;A$ .

For an $A$ -module $M$ , the unit of the adjunction is:

\begin{align*} \eta _M : M &\to \prod _{x : \mathrm{Spec}\;A} (M \otimes x) \\ m &\mapsto (m \otimes 1)_{x : \mathrm{Spec}\;A} \end{align*}

Example 7.2.2 (using SQC2, Loc1). It is not the case that for every finitely presented $R$ -algebra $A$ and every $A$ -module $M$ the map $\eta _M$ is injective.

Proof. Ingo et al. (2023).

Theorem 7.2.3 (using SQC2, Loc1, Z-choice3). Let $A$ be a finitely presented $R$ -algebra and $X = \mathrm{Spec}(A)$ . The adjunction of the previous proposition reduces to an equivalence between $A\text{-}\mathrm{Mod}_{\textrm{fp}}$ and $(R\text{-}\mathrm{Mod}_{textrm{fp}})^{X}$ . Under this correspondence, localizing $\prod _{x:X}M_x$ at $f:A$ corresponds to restricting $M$ to $D(f)$ .

Proof. If $M$ has a finite presentation $A^p\to A^q\to M\to 0$ , then $M\otimes _A x$ has the corresponding presentation $R^p\to R^q\to M\otimes _A x\to 0$ . Using Theorem 7.3.6 (one can check that there is no circularity) we see that $\Pi _{x:X}(M\otimes _A x) = M$ .

Conversely, assume that, for each $x$ , we have a finite presentation $R^{p_x}\to R^{q_x}\to M_x\to 0$ . We write $\tilde{M}$ for $\Pi _{x:X}M_x$ , and we note that $\tilde{M}_f$ is $\Pi _{x:D(f)}M_x$ for $f$ in $A$ since $M_x$ , being finitely presented, is wqc, by Proposition 7.1.13. By boundedness and local choice, we get $p,q$ and a finite open covering $D(f_1),\dots, D(f_l)$ of $X$ and $P_i:A_{f_i}^p\to A_{f_i}^q$ such that, for each $x$ in $D(f_i)$ , we have a presentation $R^p\to _{P_i(x)} R^q\to M_x\to 0$ . Using Theorem 7.3.6 we get a presentation $A_{f_i}^p\to _{P_i} A_{f_i}^q\to \tilde{M}_{f_i}\to 0$ .

Following (Lombardi and Quitté (2015), IV.4.13) we find $n,m$ and $P:A^n\rightarrow A^m$ with a presentation $A^n\to _P A^m\to \tilde{M}\to 0$ such that, for each $x$ in $X$ , we have a presentation $R^n\to _{P(x)} R^m\to M_x\to 0$ . This shows $M_x = \tilde{M}\otimes _A x$ .

7.3 Cohomology on affine schemes

Definition 7.3.1. Let $X$ be a type and $A:X\to \mathrm{Ab}$ a map to the type of abelian groups. For $x:X$ let $T_x$ be a set with an $A_x$ action.

1. (a) $T$ is an $A$ -pseudotorsor, if the action is free and transitive for all $x:X$ .

2. (b) $T$ is an $A$ -torsor, if it is an $A$ -pseudotorsor and

   \begin{equation*} \prod _{x:X} \lVert T_x \rVert \rlap {.}\end{equation*}

3. (c) We write $A\text{-}\mathrm{Tors}(X)$ for the type of $A$ -torsors on $X$ .

Torsors on a point are a concrete implementation of first deloopings:

Definition 7.3.2. Let $n:\mathbb{N}$ . A $n$ -th delooping of an abelian group $A$ , is a pointed, $(n-1)$ -connected, $n$ -truncated type $K(A,n)$ , such that $\Omega ^nK(A,n)=_{\mathrm{Ab}}A$ .

For any abelian group and any $n$ , a delooping $K(A,n)$ exists by Licata and Finster (2014). Deloopings can be used to represent cohomology groups by mapping spaces. This is usually done in homotopy type theory to study higher inductive types, such as spheres and CW-complexes, but the same approach works for internally representing sheaf cohomology, which is the intent of the following definition:

Definition 7.3.3. Let $X$ be a type and $\mathcal{F}:X\to \mathrm{Ab}$ a dependent abelian group. The $n$ -th cohomology group of $X$ with coefficients in $\mathcal{F}$ is

\begin{equation*} H^n(X,\mathcal {F})\;\colon \!\!\!\equiv\; \left \lVert \prod _{x:X}K(\mathcal {F},n)\right \rVert _0\rlap {.} \end{equation*}

Theorem 7.3.4. Let $\mathcal{F},\mathcal{G},\mathcal{H}:X\to \mathrm{Ab}$ be such that for all $x:X$ ,

\begin{equation*} 0\to \mathcal {F}_x\to \mathcal {G}_x\to \mathcal {H}_x\to 0 \end{equation*}

is an exact sequence of abelian groups. Then there is a long exact sequence:

Proof. By applying the long exact homotopy fiber sequence.

The following is an explicit formulation of the fact, that the Čech-Complex for an $\mathcal{O}_X$ -module sheaf on $X=\mathrm{Spec}(A)$ given by an $A$ -module $M$ is exact in degree 1.

Lemma 7.3.5. Let $M$ be a module over a commutative ring $A$ , $F_1,\dots, F_l$ a coprime system on $A$ and for $i,j\in \{1,\dots, l\}$ , let $s_{ij} : F_i^{-1} F_j^{-1} M$ such that:

\begin{equation*} s_{jk}-s_{ik}+s_{ij}=0 \rlap {.}\end{equation*}

Then there are $u_i:F_i^{-1}M$ such that $s_{ij}=u_j - u_i$ .

Proof. Let $s_{ij}=\frac{m_{ij}}{f_i f_j}$ with $m_{ij}:M$ , $f_i:F_i$ and $f_j:F_j$ such that:

\begin{equation*} f_i\cdot m_{jk}-f_j\cdot m_{ik}+f_k\cdot m_{ij}=0 \rlap {.}\end{equation*}

Let $r_i$ such that $\sum r_i f_i =1$ . Then for

\begin{equation*} u_i := -\sum _{k=1}^l\frac {r_k}{f_i}m_{ik} \end{equation*}

we have:

\begin{align*} u_j-u_i &= -\sum _{k=1}^l\frac{r_k}{f_j}m_{jk} + \sum _{k=1}^l\frac{r_k}{f_i}m_{ik} \\ &= -\sum _{k=1}^l\frac{r_k}{f_j f_i}f_i m_{jk} + \sum _{k=1}^l\frac{r_k}{f_i f_j} f_j m_{ik} \\ &= \sum _{k=1}^l\frac{r_k}{f_j f_i}(-f_i m_{jk} + f_j m_{ik}) \\ &= \sum _{k=1}^l\frac{r_k}{f_j f_i}f_k m_{ij} \\ &= \frac{m_{ij}}{f_i f_j} \end{align*}

Theorem 7.3.6 (using Loc, SQC, Z-choice). For any affine scheme $X=\mathrm{Spec}(A)$ and coefficients $M: X\to R\text{-}\mathrm{Mod}_{wqc}$ , we have

\begin{equation*} H^1(X,M)=0 \rlap {.} \end{equation*}

Proof. We need to show that any $M$ -torsor $T$ on $X$ is merely equal to the trivial torsor $M$ or equivalently show the existence of a section of $T$ . We have

\begin{equation*} \prod _{x:X}\lVert T_x \rVert \end{equation*}

and therefore, by (Z-choice), there merely are $f_1,\dots, f_l:A$ , such that the $U_i:= \mathrm{Spec}(A_{f_i})$ cover $X$ and there are local sections

\begin{equation*} s_i:\prod _{x:U_i}T_x\end{equation*}

of $T$ . Our goal is to construct a matching family from the $s_i$ . On intersections, let $t_{ij}:= s_i-s_j$ be the difference, so $t_{ij}:(x : U_i\cap U_j) \to M_x$ . By Lemma7.1.8 equivalently, we have $t_{ij}:M(U_{i}\cap U_j)_{f_i f_j}$ . Since the $t_{ij}$ were defined as differences, the condition in Lemma7.3.5 is satisfied and we get $u_i:M(U_i)_{f_i}$ , such that $t_{ij}=u_i-u_j$ . So we merely have a matching family $\tilde{s}_i:= s_i-u_i$ , and therefore, using Lemma1.2.2 merely a section of $T$ .

A similar result is provable for $H^2(X,M)$ using the same approach. There is an extension of this result to general $n$ in work in progress (Blechschmidt et al., 2023).

7.4 Čech-cohomology

In this section, let $X$ be a type, $U_1,\dots, U_n\subseteq X$ open subtypes that cover $X$ and $\mathcal{F}:X\to \mathrm{Ab}$ a dependent abelian group on $X$ . We start by repeating the classical definition of Čhech-Cohomology groups for a given cover.

Definition 7.4.1.

1. (a) For open $U\subseteq X$ , we use the notation from Definition 7.1.1 :

   \begin{equation*} \mathcal {F}(U)\;\colon \!\!\!\equiv\; \prod _{x:U}\mathcal {F}_x\rlap {.} \end{equation*}

2. (b) For $s:\mathcal{F}(U)$ and open $V\subseteq U$ , we use the notation $s\;\colon \!\!\!\equiv\; s_{|V} \;\colon \!\!\!\equiv\; (x:V)\mapsto s_x$ .

3. (c) For a selection of indices $i_1,\ldots, i_l:\{1,\dots, n\}$ , we use the notation

   \begin{equation*} U_{i_1\dots i_l}\;\colon \!\!\!\equiv\; U_{i_1}\cap \dots \cap U_{i_l}\rlap {.} \end{equation*}

4. (d) For a list of indices $i_1,\dots, i_l$ , let $i_1,\dots, \hat{i_t},\dots, i_l$ be the same list with the $t$ -th element removed.

5. (e) For $k:\mathbb{Z}$ , the $k$ -th Čech-boundary operator is the homomorphism

   \begin{equation*} \partial ^k:\bigoplus _{i_0,\dots, i_k}\mathcal {F}(U_{i_0\dots i_k})\to \bigoplus _{i_0,\dots, i_{k+1}}\mathcal {F}(U_{i_0\dots i_{k+1}}) \end{equation*}
   given by $\partial ^k(s)\;\colon \!\!\!\equiv\; (l_0,\dots, l_{k+1}) \mapsto \sum _{j=0}^k (-1)^j s_{l_0,\dots, \hat{l_j},\dots, l_k|U_{l_0,\dots, l_{k+1}}}$ .

6. (f) The $k$ -th Čech-Cohomology group for the cover $U_1,\dots, U_n$ with coefficients in $\mathcal{F}$ is

   \begin{equation*} \check {H}^k(\{U\},\mathcal {F})\;\colon \!\!\!\equiv\; \ker \partial ^{k} / {\mathrm {im}}(\partial ^{k-1})\rlap {.} \end{equation*}

It is possible to construct a torsor from a Čech cocycle:

Lemma 7.4.2. Let $A$ be an abelian group and $L$ a type with $\lVert L \rVert$ . Let us call $c:(i,j:L)\to A$ a $L$ -cocycle, if $c_{ij}+c_{jk}=c_{ik}$ for all $i,j,k:L$ . Then there is a bijection:

\begin{equation*} \left ((T:\text {$A$-torsor})\times T^L\right ) \to \text {$L$-cocycles} \rlap {.} \end{equation*}

Proof. Let us first check, that the left side is a set. Let $(T,u),(T',u'):(T:\text{$A$-torsor})\times T^L$ , then $(T,u)=(T',u')$ is equivalent to $(e:T\cong T')\times ((i:L)\to e(u_i)=u'_i)$ . But two maps $e$ with this property are equal, since a map between torsors is determined by the image of a single element and $L$ is inhabited.

Assume now $(T,u):(T:\text{$A$-torsor})\times T^L$ to construct the map. Then $c_{ij}\;\colon \!\!\!\equiv\; u_i-u_j$ defines an $L$ -cocycle because

\begin{equation*} u_i-u_j + u_j-u_k = u_i-u_k \rlap {.} \end{equation*}

This defines an embedding: Assume $(T,u)$ and $(T',u')$ define the same $L$ -cocycle, then $u_i-u_j=u'_i-u'_j$ for all $i,j:L$ . We want to show a proposition, so we can assume there is $i:L$ and use that to get a map $e:T\to T'$ that sends $u_i$ to $u'_i$ . But then we also have

\begin{equation*} e(u_j)=e(u_j-u_i+u_i)=e(u'_j-u'_i+u_i)=u'_j-u'_i+e(u_i)=u'_j-u'_i+u'_i=u'_j \end{equation*}

for all $j:L$ , which means $(T,u)=(T',u')$ .

Now let $c$ be an $L$ -cocycle. Following Deligne (1991)[Section 5.2], we can define a preimage-candidate:

\begin{equation*} T_c\;\colon \!\!\!\equiv\; \{u:A^L\mid u_i-u_j=c_{ij}\} \rlap {.} \end{equation*}

$A$ acts on $T_c$ pointwise, since $(a+u_i)-(a+u_j)=u_i-u_j=c_{ij}$ for all $a:A$ .

To show that $T_c$ is inhabited, we may assume $i_0:L$ . Then we define $u_i\;\colon \!\!\!\equiv\; -c_{i_0i}$ to get $u_i-u_j=-c_{i_0i}+c_{i_0j}=c_{ij}$ .

Now $c$ is of type $(A^L)^L=A^{L\times L}$ , so we have an element of the left-hand side. Applying the map constructed above yields a cocycle

\begin{equation*} \tilde {c}_{ij}=(k\mapsto c_{ki})-(k\mapsto c_{kj})=(k\mapsto c_{ki}-c_{kj})=(k\mapsto c_{kj}+c_{ji}-c_{kj})=(k\mapsto c_{ji}) \end{equation*}

– so $(T_c,c)$ is a preimage of $c_{ij}$ .

Definition 7.4.3. The cover $U_1,\dots, U_n$ is called r-acyclic for $\mathcal{F}$ , if we have the following triviality of higher (non Čech) cohomology groups:

\begin{equation*} \forall l, r\geq l\gt 0\ \forall i_0,\dots, i_{r-l}. H^l(U_{i_0,\dots, i_{r-l}},\mathcal {F})=0\rlap {.} \end{equation*}

Example 7.4.4. If $X$ is a scheme, $U_1,\dots, U_n$ a cover by affine open subtypes and $\mathcal{F}$ pointwise a weakly quasi coherent $R$ -module, then $U_1,\dots, U_n$ is 1-acyclic for $\mathcal{F}$ by Theorem 7.3.6 .

Theorem 7.4.5 (using Z-choice). If $U_1,\dots, U_n$ is a 1-acyclic cover for $\mathcal{F}$ , then

\begin{equation*} \check {H}^1(\{U\},\mathcal {F})=H^1(X,\mathcal {F})\rlap {.} \end{equation*}

Proof. Let $\pi$ be the projection map

\begin{equation*} \pi : \left ( \sum _{T:\mathcal {F}\text {-}\mathrm {Tors}(X)}\prod _{i}\prod _{x:U_i}T_x \right ) \to \mathcal {F}\text {-}\mathrm {Tors}(X)\rlap {.} \end{equation*}

Let us abbreviate the left-hand side with $T(\mathcal{F},U)$ . Since the cover is 1-acyclic, $\pi$ is surjective. With $L_x\;\colon \!\!\!\equiv\; \sum _{i}U_i(x)$ and Lemma7.4.2 we get:

\begin{align*} T(\mathcal{F},U)&=\prod _{x:X}(T_x:\mathcal{F}_x\text{-}\mathrm{Tors})\times T_x^{L_x} \\ &=\prod _{x:X}\text{$L_x$-cocycles} \rlap{.} \end{align*}

The latter is the type of Čech-1-cocycles (Definition7.4.1 (e)) and in total the equality is given by the isomorphism

\begin{equation*} (T,t) \mapsto (i,j\mapsto t_i - t_j) : T(\mathcal {F},U) \to \ker (\partial ^1) \subseteq \bigoplus _{i,j}\mathcal {F}(U_{ij})\rlap {.} \end{equation*}

Realizing, that ${\mathrm{im}}(\partial ^0)$ corresponds to the subtype of $T(\mathcal{F},U)$ of trivial torsors, we arrive at the following diagram:

The composed map $T(\mathcal{F},U)\to H^1(X,\mathcal{F})$ is a homomorphism and therefore by Lemma1.3.15 a cokernel. So the two cohomology groups are equal, since they are cokernels of the same diagram.

It is possible to pass from torsors to gerbes, which are the degree 2 analogue of torsors:

Definition 7.4.6. Let $A:\mathrm{Ab}$ be an abelian group. An $A$ -banded gerbe is a connected type $\mathcal{G}:\mathcal{U}$ , together with, for all $y:\mathcal{G}$ an identification of groups $\Omega (\mathcal{G},y)=A$ .

Analogous to the type of $A$ -torsors, the type of $A$ -banded gerbes is a second delooping of an abelian group $A$ . We can formulate a second degree version of Lemma7.4.2:

Theorem 7.4.7. Let $A$ be an abelian group and $L$ a type with $\lVert L \rVert$ . Let us call $c:(i,j,k : L)\to A$ a $L$ -2-cocycle, if $c_{jkl}-c_{ikl}+c_{ijl}-c_{ijk}=0$ for all $i,j,k,l : L$ . Then there is a bijection:

\begin{equation*} \left ((\mathcal {G}:\text {$A$-gerbe})\times (u:\mathcal {G}^{L})\times (i,j : L) \to u_i=u_j\right ) \to \text {$L$-2-cocycle} \rlap {.} \end{equation*}

This is provable, again, by translating Deligne’s argument Deligne (1991)[Section 5.3]. Using this, the correspondence of Eilenberg–MacLane-Cohomology and Čech-Cohomology can be extended in the following way:

Theorem 7.4.8. If $U_1,\dots, U_n$ is a 2-acyclic cover for $\mathcal{F}$ , then

\begin{equation*} \check {H}^2(\{U\},\mathcal {F})=H^2(X,\mathcal {F})\rlap {.} \end{equation*}

However, with this approach, we need versions of Lemma1.2.2, with increasing truncation level. While this suggests, we can prove the correspondence for any cohomology group of external degree $l$ , there is follow-up work in progress ( Blechschmidt et al., 2023), which proves the correspondence for all internal $l:\mathbb{N}$ . In the same draft, there is also a version of the vanishing result for all internal $l$ . This means that many of the usual, essential computations with Čech-Cohomology can be transferred to synthetic algebraic geometry.

8. Type Theoretic Justification of Axioms

In this section, we present a model of the 3 axioms stated in Section 2.1. This model is best described as an internal model of a presheaf model. The first part can then be described purely syntactically, starting from any model of 4 other axioms that are valid in a suitable presheaf model. We obtain then the sheaf model by defining a family of open left exact modalities, and the new model is the model of types that are modal for all these modalities. This method works both in a $1$ -topos framework and for models of univalent type theory. Throughout this section, we use the words internal and external relative to the model satisfying the 4 axioms below or state explicitly to which model they refer.

8.1 Internal sheaf model

8.1.1 Axioms for the presheaf model

We start from 4 axioms. The 3 first axioms can be seen as variation of our 3 axioms for synthetic algebraic geometric.

1. (1) $R$ is a ring,

2. (2) for any f.p. $R$ -algebra $A$ , the canonical map $A\rightarrow R^{\mathrm{Spec}(A)}$ is an equivalence

3. (3) for any f.p. $R$ -algebra $A$ , the set $\mathrm{Spec}(A)$ satisfies choice, which can be formulated as the fact that for any family of types $P(x)$ for $x:\mathrm{Spec}(A)$ there is a map $(\Pi _{x:\mathrm{Spec}(A)}\left \lVert P(x) \right \rVert )\rightarrow \left \lVert \Pi _{x:\mathrm{Spec}(A)}P(x) \right \rVert$ .

4. (4) for any f.p. $R$ -algebra $A$ , the diagonal map $\mathbb{N}\rightarrow \mathbb{N}^{\mathrm{Spec}(A)}$ is an equivalence.

As before, $\mathrm{Spec}(A)$ denotes the type of $R$ -algebra maps from $A$ to $R$ , and if $r$ is in $R$ , we write $D(r)$ for the proposition $\mathrm{Spec}(R_r)$ .

Note that the first axiom does not require $R$ to be local, and the third axiom states that $\mathrm{Spec}(A)$ satisfies choice and not only Zariski local choice, for any f.p. $R$ -algebra $A$ .

8.1.2 Justification of the axioms for the presheaf model

We justify briefly the second axiom (synthetic quasi-coherence). This justification will be done in a $1$ -topos setting, but exactly the same argument holds in the setting of presheaf models of univalent type theory, since it only involves strict presheaves. A similar direct verification holds for the other axioms.

We work with presheaves on the opposite of the category of finitely presented $k$ -algebras. We write $L,M,N,\dots$ for such objects, and $f,g,h,\dots$ for the morphisms. A presheaf $F$ on this category is given by a collection of sets $F(L)$ with restriction maps $F(L)\rightarrow F(M),\,u\mapsto f u$ for $f:L\rightarrow M$ satisfying the usual uniformity conditions. The ring $R$ is interpreted as the presheaf given by $R(L)\;\colon \!\!\!\equiv\; L$ .

We first introduce the presheaf $\mathsf{FP}$ of finite presentations. This is internally the type

\begin{equation*} \Sigma _{n:\mathbb {N}}\Sigma _{m:\mathbb {N}}R[X_1,\dots, X_n]^m \end{equation*}

which is interpreted by ${\mathsf{FP}}(L) = \Sigma _{n:\mathbb{N}}\Sigma _{m:\mathbb{N}}L[X_1,\dots, X_n]^m$ . If $\xi = (n,m,q_1,\dots, q_m)\in{\mathsf{FP}}(L)$ is such a presentation, we build a natural extension $\iota :L\rightarrow L_{\xi } = L[X_1,\dots, X_n]/(q_1,\dots, q_m)$ where the system $q_1 = \dots = q_m = 0$ has a solution $s_{\xi }$ . Furthermore, if we have another extension $f:L\rightarrow M$ and a solution $s\in M^n$ of this system in $M$ , there exists a unique map $i(f,s):L_{\xi }\rightarrow M$ such that $i(f,s) s_{\xi } = s$ and $i(f,s)\circ \iota = f$ . Note that $i(\iota, s_{\xi }) = \mathrm{id}$ .

Internally, we have a map $A:{\mathsf{FP}}\rightarrow R\mathsf{-alg}({\mathcal{U}}_0)$ , which to any presentation $\xi = (n,m,q_1,\dots, $ $q_m)$ associates the $R$ -algebra $A(\xi ) = L[X_1,\dots, X_n]/(q_1,\dots, q_m)$ . This corresponds externally to the presheaf on the category of elements of $\mathsf{FP}$ defined by $A(L,\xi ) = L_{\xi }$ .

Internally, we have a map $\mathrm{Spec}(A):{\mathsf{FP}}\rightarrow{\mathcal{U}}_0$ , defined by $\mathrm{Spec}(A)(\xi ) = Hom(A(\xi ),R)$ . We can replace it by the isomorphic map which to $\xi = (n,m,q_1,\dots, q_m)$ associates the set $S(\xi )$ of solutions of the system $q_1=\dots =q_m= 0$ in $R^n$ . Externally, this corresponds to the presheaf on the category of elements of $\mathsf{FP}$ so that $\mathrm{Spec}(A)(L,n,m,q_1,\dots, q_m)$ is the set of solutions of the system $q_1=\dots =q_m=0$ in $L^n$ .

We now define externally two inverse maps $\varphi :A(\xi )\rightarrow R^{\mathrm{Spec}(A(\xi ))}$ and $\psi :R^{\mathrm{Spec}(A(\xi ))}\rightarrow A(\xi )$ .

Notice first that $R^{\mathrm{Spec}(A)}(L,\xi )$ , for $\xi = (n,m,q_1,\dots, q_m)$ , is the set of families of elements $l_{f,s}:M$ indexed by $f:L\rightarrow M$ and $s:M^n$ a solution of $fq_1 = \dots = fq_m=0$ , satisfying the uniformity condition $g(l_{f,s}) = l_{(g\circ f),gs}$ for $g:M\rightarrow N$ .

For $u$ in $A(L,\xi ) = L_{\xi }$ we define $\varphi \,u$ in $R^{\mathrm{Spec}(A)}(L,\xi )$ by

\begin{equation*} (\varphi \,u)_{f,s} = i(f,s)\,u \end{equation*}

and for $l$ in $R^{\mathrm{Spec}(A)}(L,\xi )$ we define $\psi \,l$ in $A(L,\xi ) = L_{\xi }$ by

\begin{equation*} \psi \, l = l_{\iota, s_{\xi }} \end{equation*}

These maps are natural, and one can check

\begin{equation*} \psi \,(\varphi \,u) = (\varphi \,u)_{\iota, s_{\xi }} = i(\iota, s_{\xi })\,u = u \end{equation*}

and

\begin{equation*} (\varphi \,(\psi \,l))_{f,s} = i(f,s)\,(\psi \,l) = i(f,s)\,l_{\iota, s_{\xi }} = l_{(i(f,s)\circ \iota ),(i(f,s)\,s_{\xi })} = l_{f,s} \end{equation*}

which shows that $\varphi$ and $\xi$ are inverse natural transformations.

Furthermore, the map $\varphi$ is the external version of the canonical map $A(\xi )\rightarrow R^{\mathrm{Spec}(A(\xi ))}$ . The fact that this map is an isomorphism is an (internally) equivalent statement of the second axiom.

8.1.3 Sheaf model obtained by localisation from the presheaf model

We define now a family of propositions. As before, if $A$ is a ring, we let $\mathrm{Um}(A)$ be the type of unimodular sequences (Definition1.3.13) $f_1,\dots, f_n$ in $A$ , that is, such that $(1) = (f_1,\dots, f_n)$ . To any element $\vec{r} = r_1,\dots, r_n$ in $\mathrm{Um}(R)$ we associate the proposition $D(\vec{r}) = D(r_1)\vee \dots \vee D(r_n)$ . If $\vec{r}$ is the empty sequence, then $D(\vec{r})$ is the proposition $1 =_R 0$ .

Starting from any model of dependent type theory with univalence satisfying the 4 axioms above, we build a new model of univalent type theory by considering the types $T$ that are modal for all modalities defined by the propositions $D(\vec{r})$ , that is, such that all diagonal maps $T\rightarrow T^{D(\vec{r})}$ are equivalences. This new model is called the sheaf model.

This way of building a new sheaf model can be described purely syntactically, as in Quirin (2016). In Coquand et al. (2021), we extend this interpretation to cover inductive data types. In particular, we describe there the sheafification $\mathbb{N}_S$ of the type of natural numbers with the unit map $\eta :\mathbb{N}\rightarrow \mathbb{N}_S$ .

A similar description can be done starting with the $1$ -presheaf model. In this case, we use for the propositional truncation of a presheaf $A$ the image of the canonical map $A\rightarrow 1$ . We, however, get a model of type theory without universes when we consider modal types.

Proposition 8.1.1. The ring $R$ is modal. It follows that any f.p. $R$ -algebra is modal.

Proof. If $r_1,\dots, r_n$ is in $\mathrm{Um}(R)$ , we build a patch function $R^{D(r_1,\dots, r_n)}\rightarrow R$ . Any element $u:R^{D(r_1,\dots, r_n)}$ gives a compatible family of elements $u_i:R^{D(r_i)}$ , hence a compatible family of elements in $R_{r_i}$ by quasi-coherence. But then it follows from local-global principle Lombardi and Quitté (2015), that we can patch this family to a unique element of $R$ .

If $A$ is a f.p. $R$ -algebra, then $A$ is isomorphic to $R^{\mathrm{Spec}(A)}$ and hence is modal.

Proposition 8.1.2. In this new sheaf model, $\perp _S$ is $1 =_R 0$ .

Proof. The proposition $1=_R0$ is modal by the previous proposition. If $T$ is modal, all diagonal maps $T\rightarrow T^{D(\vec{r})}$ are equivalences. For the empty sequence $\vec{r}$ , we have that $D(\vec{r})$ is $\perp$ , and the empty sequence is unimodular exactly when $1 =_R 0$ . So $1=_R0$ implies that $T$ and $T^{\perp }$ are equivalent, and so implies that $T$ is contractible. By extensionality, we get that $(1=_R0)\rightarrow T$ is contractible when $T$ is modal.

Lemma 8.1.3. For any f.p. $R$ -algebra $A$ , we have $\mathrm{Um}(R)^{\mathrm{Spec}(A)} = \mathrm{Um}(A)$ .

Proof. Note that the fact that $r_1,\dots, r_n$ is unimodular is expressed by

\begin{equation*}\left \lVert \Sigma _{s_1,\dots, s_n:R}r_1s_1+\dots +r_ns_n = 1 \right \rVert \end{equation*}

and we can use these axioms 2 and 3 to get

\begin{equation*}\left \lVert \Sigma _{s_1,\dots, s_n:R}r_1s_1+\dots +r_ns_n = 1 \right \rVert ^{\mathrm {Spec}(A)} = \left \lVert \Sigma _{v_1,\dots, v_n:A}\Pi _{x:\mathrm {Spec}(A)}r_1v_1(x)+\dots +r_nv_n(x) = 1 \right \rVert \end{equation*}

The result follows then from this and axiom 4.

For an f.p. $R$ -algebra $A$ , we can define the type of presentations $Pr_{n,m}(A)$ as the type $A[X_1,\dots, X_n]^m$ . Each element in $Pr_{n,m}(A)$ defines an f.p. $A$ -algebra. Since $Pr_{n,m}(A)$ is a modal type since $A$ is f.p., the type of presentations $Pr_{n,m}(A)_S$ in the sheaf model defined for $n$ and $m$ in $\mathbb{N}_S$ will be such that $Pr_{\eta p,\eta q}(A)_S = Pr_{p,q}(A)$ Coquand et al. (2021).

Lemma 8.1.4. If $P$ is a proposition, then the sheafification of $P$ is

\begin{equation*}\left \lVert \Sigma _{(r_1,\dots, r_n):\mathrm {Um}(R)}P^{D(r_1,\dots, r_n)} \right \rVert \end{equation*}

Proof. If $Q$ is a modal proposition and $P\rightarrow Q$ , we have

\begin{equation*}\left \lVert \Sigma _{(r_1,\dots, r_n):\mathrm {Um}(R)}P^{D(r_1,\dots, r_n)} \right \rVert \rightarrow Q\end{equation*}

since $P^{D(r_1,\dots, r_n)}\rightarrow Q^{D(r_1,\dots, r_n)}$ and $Q^{D(r_1,\dots, r_n)}\rightarrow Q$ . It is thus enough to show that

\begin{equation*}P_0 = \left \lVert \Sigma _{(r_1,\dots, r_n):\mathrm {Um}(R)}P^{D(r_1,\dots, r_n)} \right \rVert \end{equation*}

is modal. If $s_1,\dots, s_m$ is in $\mathrm{Um}(R)$ we show $P_0^{D(s_1,\dots, s_m)}\rightarrow P_0$ . This follows from $\mathrm{Um}(R)^{D(r)} = \mathrm{Um}(R_r)$ , Lemma8.1.3.

Proposition 8.1.5. For any modal type $T$ , the proposition $\left \lVert T \right \rVert _S$ is

\begin{equation*}\left \lVert \Sigma _{(r_1,\dots, r_n):\mathrm {Um}(R)}T^{D(r_1)}\times \dots \times T^{D(r_n)} \right \rVert \end{equation*}

Proof. It follows from Lemma8.1.4 that the proposition $\left \lVert T \right \rVert _S$ is

\begin{equation*}\left \lVert \Sigma _{(r_1,\dots, r_n):\mathrm {Um}(R)}\left \lVert T \right \rVert ^{D(r_1,\dots, r_n)} \right \rVert = \left \lVert \Sigma _{(r_1,\dots, r_n):\mathrm {Um}(R)}\left \lVert T \right \rVert ^{D(r_1)}\times \dots \times \left \lVert T \right \rVert ^{D(r_n)} \right \rVert \end{equation*}

and we get the result using the fact that choice holds for each $D(r_i)$ , so that

\begin{equation*}\left \lVert T \right \rVert ^{D(r_1)}\times \dots \times \left \lVert T \right \rVert ^{D(r_n)} = \left \lVert T^{D(r_1)} \right \rVert \times \dots \times \left \lVert T^{D(r_n)} \right \rVert = \left \lVert T^{D(r_1)}\times \dots \times T^{D(r_n)} \right \rVert \end{equation*}

Proposition 8.1.6. In the sheaf model, $R$ is a local ring.

Proof. This follows from Proposition8.1.5 and Lemma8.1.3.

Lemma 8.1.7. If $A$ is a $R$ -algebra which is modal and there exists $r_1,\dots, r_n$ in $\mathrm{Um}(R)$ such that each $A^{D(r_i)}$ is a f.p. $R_{r_i}$ -algebra, then $A$ is a f.p. $R$ -algebra.

Proof. Using the local-global principles presented in Lombardi and Quitté (2015), we can patch together the f.p. $R_{r_i}$ -algebra to a global f.p. $R$ -algebra. This f.p. $R$ -algebra is modal by Proposition8.1.1 and is locally equal to $A$ and hence equal to $A$ since $A$ is modal.

Corollary 8.1.8. The type of f.p. $R$ -algebras is modal and is the type of f.p. $R$ -algebras in the sheaf model.

Proof. For any $R$ -algebra $A$ , we can form a type $\Phi (n,m,A)$ expressing that $A$ has a presentation for some $v:Pr_{n,m}(R)$ , as the type stating that there is some map $\alpha :R[X_1,\dots, X_n]\rightarrow A$ and that $(A,\alpha )$ is universal such that $\alpha$ is $0$ on all elements of $v$ . We can also look at this type $\Phi (n,m,A)_S$ in the sheaf model. Using the translation from Quirin (2016); Coquand et al. (2021), we see that the type $\Phi (\eta n,\eta m,A)_S$ is exactly the type stating that $A$ is presented by some $v:Pr_{n,m}(A)$ among the modal $R$ -algebras. This is actually equivalent to $\Phi (n,m,A)$ since any f.p. $R$ -algebra is modal.

If $A$ is a modal $R$ -algebra which is f.p. in the sense of the sheaf model, this means that we have

\begin{equation*}\left \lVert \Sigma _{n:\mathbb {N}_S}\Sigma _{m:\mathbb {N}_S}\Phi (n,m,A)_S \right \rVert _S\end{equation*}

This is equivalent to

\begin{equation*}\left \lVert \Sigma _{n:\mathbb {N}}\Sigma _{m:\mathbb {N}}\Phi (\eta n,\eta m,A)_S \right \rVert _S\end{equation*}

which in turn is equivalent to

\begin{equation*}\left \lVert \Sigma _{n:\mathbb {N}}\Sigma _{m:\mathbb {N}}\Phi (n,m,A) \right \rVert _S\end{equation*}

Using Lemma8.1.7 and Proposition8.1.5, this is equivalent to $\left \lVert \Sigma _{n:\mathbb{N}}\Sigma _{m:\mathbb{N}}\Phi (n,m,A) \right \rVert$ .

Note that the type of f.p. $R$ -algebra is universe independent.

Proposition 8.1.9. For any f.p. $R$ -algebra $A$ , the type $\mathrm{Spec}(A)$ is modal and satisfies the axiom of Zariski local choice in the sheaf model.

Proof. Let $P(x)$ be a family of types over $x:\mathrm{Spec}(A)$ and assume $\Pi _{x:\mathrm{Spec}(A)}\left \lVert P(x) \right \rVert _S$ . By Proposition8.1.5, this means $\Pi _{x:\mathrm{Spec}(A)}\left \lVert \Sigma _{(r_1,\dots, r_n):Um}P(x)^{D(r_1)}\times \dots \times P(x)^{D(r_n)} \right \rVert$ . The result follows then from choice over $\mathrm{Spec}(A)$ and Lemma8.1.3.

8.2 Presheaf models of univalence

We recall first how to build presheaf models of univalence Cohen et al., (2015); Coquand (2018), and presheaf models satisfying the 3 axioms of the previous section.

The constructive models of univalence are presheaf models parametrised by an interval object $\mathbf{I}$ (presheaf with two global distinct elements $0$ and $1$ and which is tiny) and a classifier object $\Phi$ for cofibrations. The model is then obtained as an internal model of type theory inside the presheaf model. For this, we define $C:U\rightarrow U$ , uniform in the universe $U$ , operation closed by dependent products, sums and such that $C(\Sigma _{X:U}X)$ holds. It further satisfies, for $A:U^{\mathbf{I}}$ , the transport principle

\begin{equation*} (\Pi _{i:\mathbf {I}}C(Ai))\rightarrow (A0\rightarrow A1) \end{equation*}

We get then a model of univalence by interpreting a type as a presheaf $A$ together with an element of $C(A)$ .

This is over a base category $\square$ .

If we have another category $\mathcal{C}$ , we automatically get a new model of univalent type theory by changing $\square$ to $\square \times{\mathcal{C}}$ .

A particular case is if $\mathcal{C}$ is the opposite of the category of f.p. $k$ -algebras, where $k$ is a fixed commutative ring.

We have the presheaf $R$ defined by $R(J,A) = Hom(k[X],A)$ , where $J$ is an object of $\square$ and $A$ is an object of $\mathcal{C}$ .

The presheaf $\mathbb{G}_m$ is defined by $\mathbb{G}_m(J,A) = Hom(k[X,1/X],A) = A^{\times }$ , the set of invertible elements of $A$ .

8.3 Propositional truncation

We start by giving a simpler interpretation of propositional truncation. This will simplify the proof of the validity of choice in the presheaf model.

We work in the presheaf model over a base category $\square$ , which interprets univalent type theory, with a presheaf $\Phi$ of cofibrations. The interpretation of the propositional truncation $\left \lVert T \right \rVert$ does not require the use of the interval $\mathbf{I}$ .

We recall that in the models, to be contractible can be formulated as having an operation $\mathsf{ext}(\psi, v)$ which extends any partial element $v$ of extent $\psi$ to a total element.

The (new) remark is then that to be a (h)proposition can be formulated as having instead an operation $\mathsf{ext}(u,\psi, v)$ which, now given an element $u$ , extends any partial element $v$ of extent $\psi$ to a total element.

Propositional truncation is defined as follows. An element of $\left \lVert T \right \rVert$ is either of the form $\mathsf{inc}(a)$ with $a$ in $T$ or of the form $\mathsf{ext}(u,\psi, v)$ , where $u$ is in $\left \lVert T \right \rVert$ and $\psi$ in $\Phi$ and $v$ a partial element of extent $\psi$ .

In this definition, the special constructor $\mathsf{ext}$ is a “constructor with restrictions” which satisfies $\mathsf{ext}(u,\psi, v) = v$ on the extent $\psi$ Coquand, Huber, and Mörtberg (2018).

8.4 Choice

We prove choice in the presheaf model: if $A$ is a f.p. algebra over $R$ , then we have a map

\begin{equation*} l:(\Pi _{x:\mathrm {Spec}(A)}\left \lVert P \right \rVert )\rightarrow \left \lVert \Pi _{x:\mathrm {Spec}(A)}P \right \rVert \end{equation*}

For defining the map $l$ , we define $l(v)$ by induction on $v$ . The element $v$ is in $(\Pi _{x:\mathrm{Spec}(A)}\left \lVert P \right \rVert )(B)$ , which can be seen as an element of $\left \lVert P \right \rVert (A)$ . If it is $\mathsf{inc}(u)$ , we associate $\mathsf{inc}(u)$ and if it is $\mathsf{ext}(u,\psi, v)$ the image is $\mathsf{ext}(l(u),\psi, l(v))$ .

8.5 1-topos model

For any small category $\mathcal{C}$ , we can form the presheaf model of type theory over the base category $\mathcal{C}$ Hofmann (1997); Huber (2016).

We look at the special case where $\mathcal{C}$ is the opposite of the category of finitely presented $k$ -algebras for a fixed ring $k$ .

In this model, we have a presheaf $R(A) = Hom(k[X],A)$ , which has a ring structure.

In the presheaf model, we can check that we have $\neg \neg (0=_R 1)$ . Indeed, at any stage $A$ , we have a map $\alpha :A\rightarrow 0$ to the trivial f.p. algebra $0$ , and $0 =_R 1$ is valid at the stage $0$ .

The previous internal description of the sheaf model applies as well in the $1$ -topos setting.

However, the type of modal types in a given universe is not modal in this $1$ -topos setting. This problem can actually be seen as a motivation for introducing the notion of stacks and is solved when we start from a constructive model of univalence.

8.6 Some properties of the sheaf model

8.6.1 Quasi-coherence

A module $M$ in the sheaf model defined at stage $A$ , where $A$ is a f.p. $k$ -algebra, is given by a sheaf over the category of elements of $A$ . It is thus given by a family of modules $M(B,\alpha )$ , for $\alpha :A\rightarrow B$ , and restriction maps $M(B,\alpha )\rightarrow M(C,\gamma \alpha )$ for $\gamma :B\rightarrow C$ . In general, this family is not determined by its value $M_A = M(A,\mathsf{id}_A)$ at $A,\mathsf{id}_A$ . The next proposition expresses internally in the sheaf model, when a module has this property. This characterisation is due to Blechschmidt Blechschmidt (2017).

Proposition 8.6.1. $M$ is internally quasi-coherent ⁸ iff we have $M(B,\alpha ) = M_A\otimes _A B$ and the restriction map for $\gamma :B\rightarrow C$ is $M_A\otimes _A\gamma$ .

8.6.2 Projective space

We have defined $\mathbb{P}^n$ to be the set of lines in $V = R^{n+1}$ , so we have

\begin{equation*} \mathbb {P}^n \,=\, \Sigma _{L:V\rightarrow \Omega }[\exists _{v:V}\neg (v = 0)\wedge L = R v] \end{equation*}

The following was noticed in Kock and Reyes (1977).

Proposition 8.6.2. $\mathbb{P}^n(A)$ is the set of submodules of $A^{n+1}$ factor direct in $A^{n+1}$ and of rank $1$ .

Proof. $\mathbb{P}^n$ is the set of pairs $L,0$ , where $L:\Omega ^V(A)$ satisfies the proposition $\exists _{v:V}\neg (v = 0)\wedge L = Rv$ at stage $A$ . This condition implies that $L$ is a quasicoherent submodule of $R^{n+1}$ defined at stage $A$ . It is thus determined by its value $L(A,\mathsf{id}_A) = L_A$ .

Furthermore, the condition also implies that $L_A$ is locally free of rank $1$ . By local-global principle Lombardi and Quitté (2015), $L_A$ is finitely generated. We can then apply Theorem 5.14 of Lombardi and Quitté (2015) to deduce that $L_A$ is factor direct in $A^{n+1}$ and of rank $1$ .

One point in this argument was to notice that the condition

\begin{equation*} \exists _{v:V}\neg (v = 0)\wedge L = R v \end{equation*}

implies that $L$ is quasi-coherent. This would be direct in presence of univalence, since we would have then $L = R$ as a $R$ -module and $R$ is quasi-coherent. But it can also be proved without univalence by transport along isomorphism: a $R$ -module which is isomorphic to a quasi-coherent module is itself quasi-coherent.

8.7 Global sections and Zariski global choice

We let $\Box T$ the type of global sections of a globally defined sheaf $T$ . If $c = r_1,\dots, r_n$ is in $\mathrm{Um}(R)$ , we let $\Box _c T$ be the type $\Box T^{D(r_1)}\times \dots \times \Box T^{D(r_n)}$ .

Using these notations, we can state the principle of Zariski global choice

\begin{equation*} (\Box \left \lVert T \right \rVert )\leftrightarrow \left \lVert \Sigma _{c:\mathrm {Um}(k)}\Box _c T \right \rVert \end{equation*}

This principle is valid in the present model.

Using this principle, we can show that $\Box K(\mathbb{G}_m,1)$ is equal to the type of projective modules of rank $1$ over $k$ and that each $\Box K(R,n)$ for $n\gt 0$ is contractible.