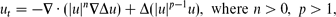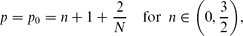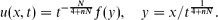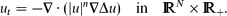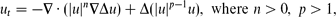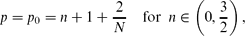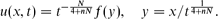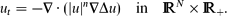When ceramics are heated inside a microwave cavity, a well-known phenomenon is the occurrence of hot spots – localised regions of high temperature. This phenomenon was modelled by Kriegsmann ((1997), IMA J. Appl. Math. 59(2), pp. 123–146; (2001), IMA J. Appl. Math. 66(1), pp. 1–32) using a non-local evolution PDE. We investigate profile and the stability of hot spots in one and two dimensions by using Kriegsmann's model with exponential non-linearity. The linearised problem associated with hot-spot-type solutions possesses two classes of eigenvalues. The first type is the large eigenvalues associated with the stability of the hot-spot profile and in this particular model there cannot be instability associated with these eigenvalues. The second type is the small eigenvalues associated with translation invariance. We show that the hot spots can become unstable due to the presence of small eigenvalues, and we characterise the instability thresholds. In particular, we show that for the material with low heat conductivity (such as ceramics), and in the presence of a variable electric field, the hot spots are typically stable inside a plate (in two dimensions) but can become unstable for a slab (in one dimension) provided that the microwave power is sufficiently large. On the other hand, for materials with high heat conductivity, the interior hot spots are unstable and move to the boundary of the domain in either one or two dimensions. For materials with moderate heat conductivity, the stability of hot spots is determined by both the geometry and the electric field inside the microwave cavity.

We consider the fourth-order thin film equation, with a stable second-order diffusion term. For the first critical exponent, where N ≥ 1 is the space dimension, the Cauchy problem is shown to admit countable continuous branches of source-type self-similar very singular solutions of the form These solutions are inherently oscillatory in nature and will be shown in Part II to be the limit of appropriate free-boundary problem solutions. For p ≠ p0, the set of very singular solutions is shown to be finite and to be consisting of a countable family of branches (in the parameter p) of similarity profiles that originate at a sequence of critical exponents {pl, l ≥ 0}. At p = pl, these branches appear via a non-linear bifurcation mechanism from a countable set of similarity solutions of the second kind of the pure thin film equation Such solutions are detected by the ‘Hermitian spectral theory’, which allows an analytical n-branching approach. As such, a continuous path as n → 0+ can be constructed from the eigenfunctions of the linear rescaled operator for n = 0, i.e. for the bi-harmonic equation ut = −Δ2u. Numerics are used, wherever appropriate, to support the analysis.

We discuss the fourth-order thin film equation with a stable second-order diffusion term, in the context of a standard free-boundary problem with zero height, zero contact angle and zero-flux conditions imposed at an interface. For the first critical exponent where N ≥ 1 is the space dimension, there are continuous sets (branches) of source-type very singular self-similar solutions of the form For p ≠ p0, the set of very singular self-similar solutions is shown to be finite and consists of a countable family of branches (in the parameter p) of similarity profiles that originate at a sequence of critical exponents {pl, l ≥ 0}. At p = pl, these branches appear via a non-linear bifurcation mechanism from a countable set of second kind similarity solutions of the pure thin film equation Such solutions are detected by a combination of linear and non-linear ‘Hermitian spectral theory’, which allows the application of an analytical n-branching approach. In order to connect with the Cauchy problem in Part I, we identify the cauchy problem solutions as suitable ‘limits’ of the free-boundary problem solutions.

We discuss the lithium storage process within a single-particle cathode of a lithium-ion battery. The single storage particle consists of a crystal lattice whose interstitial lattice sites may be empty or reversibly filled with lithium atoms. The resulting evolution equations describe diffusion with mechanical coupling and incorporate volume changes, phase transitions and surface tension. In order to simulate the dynamics, we assume spherical symmetry and fast bulk diffusion of the lithium atoms, which lead to a core shell model. We verify the common assumption of phase nucleation at the external boundary of the particle. This model is capable to predict voltage–capacity behaviour. For slow charging rates, we compare the results with experimental voltage–capacity plots exhibiting hysteretic behaviour. We observe that hysteresis cannot be described within the setting of a single-particle cathode. The origin of this fact is discussed in detail. The result is of enormous importance because single-particle models, in particular core shell models, up to now are very popular in the chemical literature.