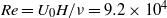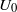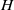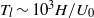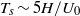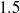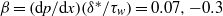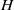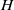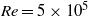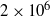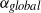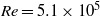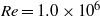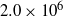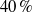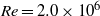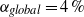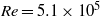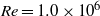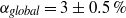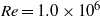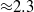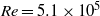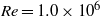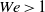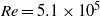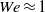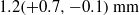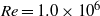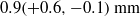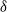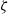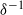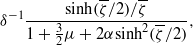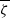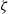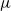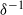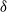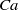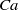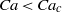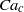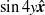We consider electrokinetic flows about a freely suspended liquid drop, deriving a macroscale description in the thin-double-layer limit where the ratio 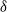 $\delta $ between Debye width and drop size is asymptotically small. In this description, the electrokinetic transport occurring within the diffuse part of the double layer (the ‘Debye layer’) is represented by effective boundary conditions governing the pertinent fields in the electro-neutral bulk, wherein the generally non-uniform distribution of
$\delta $ between Debye width and drop size is asymptotically small. In this description, the electrokinetic transport occurring within the diffuse part of the double layer (the ‘Debye layer’) is represented by effective boundary conditions governing the pertinent fields in the electro-neutral bulk, wherein the generally non-uniform distribution of 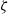 $\zeta $, the dimensionless zeta potential, is a priori unknown. We focus upon highly conducting drops. Since the tangential electric field vanishes at the drop surface, the viscous stress associated with Debye-scale shear, driven by Coulomb body forces, cannot be balanced locally by Maxwell stresses. The requirement of microscale stress continuity therefore brings about a unique velocity scaling, where the standard electrokinetic scale is amplified by a
$\zeta $, the dimensionless zeta potential, is a priori unknown. We focus upon highly conducting drops. Since the tangential electric field vanishes at the drop surface, the viscous stress associated with Debye-scale shear, driven by Coulomb body forces, cannot be balanced locally by Maxwell stresses. The requirement of microscale stress continuity therefore brings about a unique velocity scaling, where the standard electrokinetic scale is amplified by a 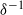 ${\delta }^{- 1} $ factor. This reflects a transition from slip-driven electro-osmotic flows to shear-induced motion. The macroscale boundary conditions display distinct features reflecting this unique scaling. The effective shear-continuity condition introduces a Lippmann-type stress jump, appearing as a product of the local charge density and electric field. This term, representing the excess Debye-layer shear, follows here from a systematic coarse-graining procedure starting from the exact microscale description, rather than from thermodynamic considerations. The Neumann condition governing the bulk electric field is inhomogeneous, representing asymptotic matching with transverse ionic fluxes emanating from the Debye layer; these fluxes, in turn, are associated with non-uniform tangential ‘surface’ currents within this layer. Their appearance at leading order is a manifestation of dominant advection associated with the large velocity scale. For weak fields, the linearized macroscale equations admit an analytic solution, yielding a closed-form expression for the electrophoretic velocity. When scaled by Smoluchowski’s speed, it reads
${\delta }^{- 1} $ factor. This reflects a transition from slip-driven electro-osmotic flows to shear-induced motion. The macroscale boundary conditions display distinct features reflecting this unique scaling. The effective shear-continuity condition introduces a Lippmann-type stress jump, appearing as a product of the local charge density and electric field. This term, representing the excess Debye-layer shear, follows here from a systematic coarse-graining procedure starting from the exact microscale description, rather than from thermodynamic considerations. The Neumann condition governing the bulk electric field is inhomogeneous, representing asymptotic matching with transverse ionic fluxes emanating from the Debye layer; these fluxes, in turn, are associated with non-uniform tangential ‘surface’ currents within this layer. Their appearance at leading order is a manifestation of dominant advection associated with the large velocity scale. For weak fields, the linearized macroscale equations admit an analytic solution, yielding a closed-form expression for the electrophoretic velocity. When scaled by Smoluchowski’s speed, it reads 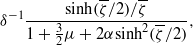 $${\delta }^{- 1} \frac{\sinh ( \overline{\zeta } / 2)/ \overline{\zeta } }{1+ { \textstyle\frac{3}{2} }\mu + 2\alpha {\mathop{\sinh }\nolimits }^{2} ( \overline{\zeta } / 2)} ,$$
$${\delta }^{- 1} \frac{\sinh ( \overline{\zeta } / 2)/ \overline{\zeta } }{1+ { \textstyle\frac{3}{2} }\mu + 2\alpha {\mathop{\sinh }\nolimits }^{2} ( \overline{\zeta } / 2)} ,$$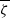 $ \overline{\zeta } $, the ‘drop zeta potential’, is the uniform value of
$ \overline{\zeta } $, the ‘drop zeta potential’, is the uniform value of 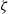 $\zeta $ in the absence of an applied field,
$\zeta $ in the absence of an applied field, 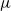 $\mu $ the ratio of drop to electrolyte viscosities, and
$\mu $ the ratio of drop to electrolyte viscosities, and  $\alpha $ the ionic drag coefficient. The difference from solid-particle electrophoresis is manifested in two key features: the
$\alpha $ the ionic drag coefficient. The difference from solid-particle electrophoresis is manifested in two key features: the 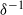 ${\delta }^{- 1} $ scaling, and the effect of ionic advection, as represented by the appearance of
${\delta }^{- 1} $ scaling, and the effect of ionic advection, as represented by the appearance of  $\alpha $. Remarkably, our result differs from the small-
$\alpha $. Remarkably, our result differs from the small-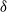 $\delta $ limit of the mobility expression predicted by the weak-field model of Ohshima, Healy & White (J. Chem. Soc. Faraday Trans. 2, vol. 80, 1984, pp. 1643–1667). This discrepancy is related to the dominance of advection on the bulk scale, even for weak fields, which feature cannot be captured by a linear theory. The order of the respective limits of thin double layers and weak applied fields is not interchangeable.
$\delta $ limit of the mobility expression predicted by the weak-field model of Ohshima, Healy & White (J. Chem. Soc. Faraday Trans. 2, vol. 80, 1984, pp. 1643–1667). This discrepancy is related to the dominance of advection on the bulk scale, even for weak fields, which feature cannot be captured by a linear theory. The order of the respective limits of thin double layers and weak applied fields is not interchangeable.