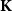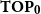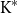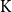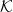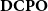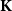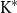1. Introduction
Non-determinism is an important semantic concept in Theoretical Computer Science and domain theory. This concept offers new insights in designing more powerful programming languages. Pioneering mathematical, in particular, domain-theoretic models considered for non-determinism were due to Plotkin and Smyth in Plotkin (Reference Plotkin1976) and Smyth (Reference Smyth1976). In order to capture the possibilities of multiple outputs in non-deterministic computations, concrete powerdomains have been introduced by Hennessy and Plotkin in (1979), and each of these constructions gives rise to a monad. Nowadays, it has been routine to use monads to give denotational semantics to computational effects like non-determinism, and different powerdomain constructions have been proposed, for example, the Hoare, Plotkin, Smyth and Probabilistic powerdomain constructions in domain theory, to name a few.
Generalizing Hennessy and Plotkin’s work, in Schalk (Reference Schalk1993), Andrea Schalk studied the Hoare power construction on the category
![]() $\mathbf{DCPO}$
of all dcpos and Scott-continuous maps, a general and versatile setting for denotational semantics. She proved that for a dcpo D, the Hoare powerdomain
$\mathbf{DCPO}$
of all dcpos and Scott-continuous maps, a general and versatile setting for denotational semantics. She proved that for a dcpo D, the Hoare powerdomain
![]() $\mathcal H(D)$
of D, comprised of all Scott closed subsets of D under set inclusion, is the free inflationary semilattice of D and useful in modeling the so-called angelic non-determinism.
$\mathcal H(D)$
of D, comprised of all Scott closed subsets of D under set inclusion, is the free inflationary semilattice of D and useful in modeling the so-called angelic non-determinism.
The Hoare powerdomain construction itself, seemingly being order-theoretic, can be factored through its topological counterpart
![]() $\mathcal H_t$
. For a topological space X,
$\mathcal H_t$
. For a topological space X,
![]() $\mathcal H_t(X)$
is the set of all closed subsets of X equipped with the lower Vietoris topology. The construction
$\mathcal H_t(X)$
is the set of all closed subsets of X equipped with the lower Vietoris topology. The construction
![]() $\mathcal H_t$
is restricted to an endofunctor on the category
$\mathcal H_t$
is restricted to an endofunctor on the category
![]() $\mathbf{MCS}$
of monotone convergence spaces, and then,
$\mathbf{MCS}$
of monotone convergence spaces, and then,
![]() $\mathcal H$
can be realized as the composite
$\mathcal H$
can be realized as the composite
![]() $\Omega \circ \mathcal H_t \circ \Sigma$
, where
$\Omega \circ \mathcal H_t \circ \Sigma$
, where
![]() $\Sigma$
assigns to each dcpo L the topological space
$\Sigma$
assigns to each dcpo L the topological space
![]() $(L, \sigma (L))$
(
$(L, \sigma (L))$
(
![]() $\sigma (L)$
is the Scott topology on L), and
$\sigma (L)$
is the Scott topology on L), and
![]() $\Omega$
assigns to each monotone convergence space X the dcpo
$\Omega$
assigns to each monotone convergence space X the dcpo
![]() $(X, \leq)$
with
$(X, \leq)$
with
![]() $\leq$
being the specialization order on X. Both
$\leq$
being the specialization order on X. Both
![]() $\Sigma$
and
$\Sigma$
and
![]() $\Omega$
leave morphisms intact. It is easy to see that
$\Omega$
leave morphisms intact. It is easy to see that
![]() $\Sigma$
is left adjoint to
$\Sigma$
is left adjoint to
![]() $\Omega$
.
$\Omega$
.

It is interesting to see that many other constructions in domain theory actually arise in a similar fashion. For example, replacing
![]() $\mathcal H_t$
by the sobrification monad
$\mathcal H_t$
by the sobrification monad
![]() $\mathcal S_t$
on
$\mathcal S_t$
on
![]() $\mathbf{MCS}$
(this makes sense as all sober spaces are monotone convergence spaces), the composite
$\mathbf{MCS}$
(this makes sense as all sober spaces are monotone convergence spaces), the composite
![]() $\Omega \circ \mathcal S_t \circ \Sigma$
gives the so-called order-sobrification monad
$\Omega \circ \mathcal S_t \circ \Sigma$
gives the so-called order-sobrification monad
![]() $\mathcal S$
on
$\mathcal S$
on
![]() $\mathbf{DCPO}$
(Ho et al. Reference Ho, Goubault-Larrecq, Jung and Xi2018). While
$\mathbf{DCPO}$
(Ho et al. Reference Ho, Goubault-Larrecq, Jung and Xi2018). While
![]() $\mathcal H$
is useful in denotational semantics,
$\mathcal H$
is useful in denotational semantics,
![]() $\mathcal S$
is employed heavily in giving a satisfactory answer to the Ho-Zhao problem by Ho et al. (Reference Ho, Goubault-Larrecq, Jung and Xi2018). That useful application also motivated Jia to systematically investigate the order-sobrification monad
$\mathcal S$
is employed heavily in giving a satisfactory answer to the Ho-Zhao problem by Ho et al. (Reference Ho, Goubault-Larrecq, Jung and Xi2018). That useful application also motivated Jia to systematically investigate the order-sobrification monad
![]() $\mathcal S$
in Jia (Reference Jia2020).
$\mathcal S$
in Jia (Reference Jia2020).
Canonical categorical reasoning tells us that for each monad
![]() $\mathcal T$
on
$\mathcal T$
on
![]() $\mathbf{MCS}$
, the composite
$\mathbf{MCS}$
, the composite
![]() $\Omega \circ \mathcal T \circ \Sigma$
actually gives rise to a monad on the category
$\Omega \circ \mathcal T \circ \Sigma$
actually gives rise to a monad on the category
![]() $\mathbf{DCPO}$
. In this paper, we mainly investigate the monads of this specific form, with
$\mathbf{DCPO}$
. In this paper, we mainly investigate the monads of this specific form, with
![]() $\mathcal T$
a reflector on the category
$\mathcal T$
a reflector on the category
![]() $\mathbf{MCS}$
. As the sobrification functor is a reflector on
$\mathbf{MCS}$
. As the sobrification functor is a reflector on
![]() $\mathbf{MCS}$
, the order-sobrification monad considered in Ho et al. (Reference Ho, Goubault-Larrecq, Jung and Xi2018) and Jia (Reference Jia2020) will be subsumed under our work. Indeed, inspired by the reflectivity of SOB in
$\mathbf{MCS}$
, the order-sobrification monad considered in Ho et al. (Reference Ho, Goubault-Larrecq, Jung and Xi2018) and Jia (Reference Jia2020) will be subsumed under our work. Indeed, inspired by the reflectivity of SOB in
![]() $\mathbf{TOP}_{\mathbf{0}}$
, reflectors on
$\mathbf{TOP}_{\mathbf{0}}$
, reflectors on
![]() $\mathbf{TOP}_{\mathbf{0}}$
or equivalently, reflective subcategories of
$\mathbf{TOP}_{\mathbf{0}}$
or equivalently, reflective subcategories of
![]() $T_0$
topological spaces have been studied extensively in domain theory. In particular, it was Keimel and Lawson who first tried to find a class of reflective subcategories in a unified form. They identified in Keimel and Lawson (Reference Keimel and Lawson2009) the following four properties and proved that each subcategory
$T_0$
topological spaces have been studied extensively in domain theory. In particular, it was Keimel and Lawson who first tried to find a class of reflective subcategories in a unified form. They identified in Keimel and Lawson (Reference Keimel and Lawson2009) the following four properties and proved that each subcategory
![]() $\mathbf K$
of
$\mathbf K$
of
![]() $\mathbf{TOP}_{\mathbf{0}}$
satisfying them is actually reflective (the objects of
$\mathbf{TOP}_{\mathbf{0}}$
satisfying them is actually reflective (the objects of
![]() $\mathbf K$
are called
$\mathbf K$
are called
![]() $\mathbf{K}$
-spaces).
$\mathbf{K}$
-spaces).
(
![]() $K_1$
) Homeomorphic copies of
$K_1$
) Homeomorphic copies of
![]() $\mathbf{K}$
-spaces are
$\mathbf{K}$
-spaces are
![]() $\mathbf{K}$
-spaces.
$\mathbf{K}$
-spaces.
(
![]() $K_2$
) All sober spaces are
$K_2$
) All sober spaces are
![]() $\mathbf{K}$
-spaces.
$\mathbf{K}$
-spaces.
(
![]() $K_3$
) In a sober space S, the intersection of any family of
$K_3$
) In a sober space S, the intersection of any family of
![]() $\mathbf{K}$
-subspaces is a
$\mathbf{K}$
-subspaces is a
![]() $\mathbf{K}$
-space.
$\mathbf{K}$
-space.
(
![]() $K_4$
) Continuous maps
$K_4$
) Continuous maps
![]() $f: S\rightarrow T$
between sober spaces S and T are
$f: S\rightarrow T$
between sober spaces S and T are
![]() $\mathbf{K}$
-continuous, that is, for every
$\mathbf{K}$
-continuous, that is, for every
![]() $\mathbf{K}$
-subspace K of T, the inverse image
$\mathbf{K}$
-subspace K of T, the inverse image
![]() $f^{-1}(K)$
is a
$f^{-1}(K)$
is a
![]() $\mathbf{K}$
-subspace of S.
$\mathbf{K}$
-subspace of S.
Later, Xu focused on the subcategories satisfying
![]() $(K_2)$
, proposed the concept of adequateness, and proved that each adequate category
$(K_2)$
, proposed the concept of adequateness, and proved that each adequate category
![]() $\mathbf K$
is reflective in
$\mathbf K$
is reflective in
![]() $\mathbf{TOP}_{\mathbf{0}}$
(Xu Reference Xu2020). More recently, Ershov raised the concept of wide categories and defined
$\mathbf{TOP}_{\mathbf{0}}$
(Xu Reference Xu2020). More recently, Ershov raised the concept of wide categories and defined
![]() $\mathbf K$
-completions in them, in which he also introduced the notion of ample
$\mathbf K$
-completions in them, in which he also introduced the notion of ample
![]() $\mathbf K$
-precompletion. He proved that each wide category admitting an ample
$\mathbf K$
-precompletion. He proved that each wide category admitting an ample
![]() $\mathbf K$
-precompletion is reflective in
$\mathbf K$
-precompletion is reflective in
![]() $\mathbf{Top}_{\mathbf{0}}$
(Ershov Reference Ershov2022). Then, the existence of D-completions (Ershov Reference Ershov1999; Wyler Reference Wyler1979),
$\mathbf{Top}_{\mathbf{0}}$
(Ershov Reference Ershov2022). Then, the existence of D-completions (Ershov Reference Ershov1999; Wyler Reference Wyler1979),
![]() $\mathbf D_b$
-completions (Keimel and Lawson Reference Keimel and Lawson2009), and WF-completions (Liu et al. Reference Liu, Li and Wu2020; Wu et al. Reference Wu, Xi, Xu and Zhao2020) can be realized as corollaries to the aforementioned results. Actually, we will see that the properties of being wide and of possessing an ample
$\mathbf D_b$
-completions (Keimel and Lawson Reference Keimel and Lawson2009), and WF-completions (Liu et al. Reference Liu, Li and Wu2020; Wu et al. Reference Wu, Xi, Xu and Zhao2020) can be realized as corollaries to the aforementioned results. Actually, we will see that the properties of being wide and of possessing an ample
![]() $\mathbf K$
-precompletion are not only sufficient conditions for a full subcategory
$\mathbf K$
-precompletion are not only sufficient conditions for a full subcategory
![]() $\mathbf K$
to be reflective but also the necessary ones. Indeed, different completions considered by Keimel and Lawson (Reference Keimel and Lawson2009), Xu (Reference Xu2020) and Ershov (Reference Ershov2022) are equivalent.
$\mathbf K$
to be reflective but also the necessary ones. Indeed, different completions considered by Keimel and Lawson (Reference Keimel and Lawson2009), Xu (Reference Xu2020) and Ershov (Reference Ershov2022) are equivalent.
Given a reflective subcategory
![]() $\mathbf K$
of
$\mathbf K$
of
![]() $\mathbf{TOP}_{\mathbf{0}}$
, the corresponding reflector
$\mathbf{TOP}_{\mathbf{0}}$
, the corresponding reflector
![]() $\mathcal K_t$
, sending each
$\mathcal K_t$
, sending each
![]() $T_0$
topological space X to its
$T_0$
topological space X to its
![]() $\mathbf{K}$
-ification (many authors also call it the
$\mathbf{K}$
-ification (many authors also call it the
![]() $\mathbf{K}$
-space completion), is a monad on
$\mathbf{K}$
-space completion), is a monad on
![]() $\mathbf{TOP}_{\mathbf{0}}$
(modulo post-composing with the obvious inclusion functor). The
$\mathbf{TOP}_{\mathbf{0}}$
(modulo post-composing with the obvious inclusion functor). The
![]() $\mathbf{K}$
-ification proves to be useful in denotational semantics, for example, Jia, Lindenhovius, Mislove, and Zamdzhiev employed
$\mathbf{K}$
-ification proves to be useful in denotational semantics, for example, Jia, Lindenhovius, Mislove, and Zamdzhiev employed
![]() $\mathbf{K}$
-ifications to construct commutative probabilistic monads for probabilistic programming languages, solving a long-standing open problem in denotational semantics (Jia et al. 2021).
$\mathbf{K}$
-ifications to construct commutative probabilistic monads for probabilistic programming languages, solving a long-standing open problem in denotational semantics (Jia et al. 2021).
Starting with a monotone convergence space, however, it is not always the case that
![]() $\mathcal K_t$
would return a monotone convergence space (see Xu et al. Reference Xu, Shen, Xi and Zhao2020 for example); hence,
$\mathcal K_t$
would return a monotone convergence space (see Xu et al. Reference Xu, Shen, Xi and Zhao2020 for example); hence,
![]() $\mathcal K_t$
cannot be restricted on
$\mathcal K_t$
cannot be restricted on
![]() $\mathbf{MCS}$
in general, nor
$\mathbf{MCS}$
in general, nor
![]() $\Omega \circ \mathcal K_t \circ \Sigma$
can be well-defined. To avoid that, we consider full subcategories satisfying
$\Omega \circ \mathcal K_t \circ \Sigma$
can be well-defined. To avoid that, we consider full subcategories satisfying
![]() $(K_1), (K_2)$
and Xu’s adequateness that are also contained in MCS to ensure that the resulting reflectors return monotone convergence spaces, and call such categories of type
$(K_1), (K_2)$
and Xu’s adequateness that are also contained in MCS to ensure that the resulting reflectors return monotone convergence spaces, and call such categories of type
![]() $\mathrm K^*$
. Now
$\mathrm K^*$
. Now
![]() $\mathcal K_t$
induces a monad
$\mathcal K_t$
induces a monad
![]() $\mathcal K$
on
$\mathcal K$
on
![]() $\mathbf {DCPO}$
, which is called order-
$\mathbf {DCPO}$
, which is called order-
![]() $\mathbf K$
-ification monad. It can also be seen that the monad
$\mathbf K$
-ification monad. It can also be seen that the monad
![]() $\mathcal K$
refines
$\mathcal K$
refines
![]() $\mathcal H$
, in the sense that for a dcpo D,
$\mathcal H$
, in the sense that for a dcpo D,
![]() $\mathcal K$
actually picks a certain subdcpo of
$\mathcal K$
actually picks a certain subdcpo of
![]() $\mathcal H(D)$
, according to the given category of type
$\mathcal H(D)$
, according to the given category of type
![]() $\mathrm K^*$
. Hence, like the Hoare powerdomain monad
$\mathrm K^*$
. Hence, like the Hoare powerdomain monad
![]() $\mathcal H$
, monad
$\mathcal H$
, monad
![]() $\mathcal K$
may also find its uses in semantics.
$\mathcal K$
may also find its uses in semantics.
In this paper, we systematically investigate the order-
![]() ${\mathbf K}$
-ification monads induced by categories of type
${\mathbf K}$
-ification monads induced by categories of type
![]() $\mathrm K^*$
. For each category of type
$\mathrm K^*$
. For each category of type
![]() $\mathrm K^*$
, we characterize the Eilenberg-Moore algebras of the resulting
$\mathrm K^*$
, we characterize the Eilenberg-Moore algebras of the resulting
![]() $\mathcal K$
and the corresponding algebraic homomorphisms, from which we obtain that the Eilenberg-Moore category is precisely
$\mathcal K$
and the corresponding algebraic homomorphisms, from which we obtain that the Eilenberg-Moore category is precisely
![]() $\mathbf{KCPO}$
of k-complete posets and k-continuous maps. In addition, we find that each category
$\mathbf{KCPO}$
of k-complete posets and k-continuous maps. In addition, we find that each category
![]() $\mathbf{KCPO}_{\sigma}$
consisting of all k-complete posets and Scott-continuous maps is Cartesian closed; thus, it could be a model for the
$\mathbf{KCPO}_{\sigma}$
consisting of all k-complete posets and Scott-continuous maps is Cartesian closed; thus, it could be a model for the
![]() $\lambda$
-calculus. We also verify that
$\lambda$
-calculus. We also verify that
![]() $\mathcal{K}$
is always a commutative monad. Hence, each monad
$\mathcal{K}$
is always a commutative monad. Hence, each monad
![]() $\mathcal K$
in this form on the category of dcpos serves as a
$\mathcal K$
in this form on the category of dcpos serves as a
![]() $\lambda_c$
-model in the sense of Moggi (Reference Moggi1989). In particular, when the category of type
$\lambda_c$
-model in the sense of Moggi (Reference Moggi1989). In particular, when the category of type
![]() $\mathrm K^*$
is chosen to be
$\mathrm K^*$
is chosen to be
![]() $\mathbf{SOB}$
, our order-
$\mathbf{SOB}$
, our order-
![]() $\mathbf{SOB}$
-ification monad is exactly the order-sobrification monad
$\mathbf{SOB}$
-ification monad is exactly the order-sobrification monad
![]() $\mathcal{S}$
proposed in Ho et al. (Reference Ho, Goubault-Larrecq, Jung and Xi2018), and all of our results generalize that of Jia in (2020).
$\mathcal{S}$
proposed in Ho et al. (Reference Ho, Goubault-Larrecq, Jung and Xi2018), and all of our results generalize that of Jia in (2020).
2. Preliminaries
Let us introduce the concepts and notions to be used in this paper.
Let P be a poset. A subset A of P is called an upper set (resp., a lower set) if
![]() $A = {\uparrow}A$
(resp.,
$A = {\uparrow}A$
(resp.,
![]() $A = {\downarrow}A$
), where
$A = {\downarrow}A$
), where
![]() ${\uparrow}A = \{x\in P: x\geq a\ \mathrm{for \ some}\ a\in A\}$
(resp.,
${\uparrow}A = \{x\in P: x\geq a\ \mathrm{for \ some}\ a\in A\}$
(resp.,
![]() ${\downarrow}A = \{x\in P: x\leq a\ \mathrm{for \ some}\ a\in A\}$
). A nonempty subset D of P is said to be directed if for each finite subset
${\downarrow}A = \{x\in P: x\leq a\ \mathrm{for \ some}\ a\in A\}$
). A nonempty subset D of P is said to be directed if for each finite subset
![]() $F\subseteq D$
there exists some
$F\subseteq D$
there exists some
![]() $d\in D$
such that
$d\in D$
such that
![]() $F\subseteq {\downarrow}d$
. Then P is directed complete (or a dcpo) if every directed subset D of P has a least upper bound, that is,
$F\subseteq {\downarrow}d$
. Then P is directed complete (or a dcpo) if every directed subset D of P has a least upper bound, that is,
![]() $\sup D$
exists in P. Let
$\sup D$
exists in P. Let
![]() $\sigma(P)$
denote the Scott topology on P, where every U in
$\sigma(P)$
denote the Scott topology on P, where every U in
![]() $\sigma(P)$
, called Scott open, satisfies
$\sigma(P)$
, called Scott open, satisfies
![]() $U = {\uparrow}U$
and for any directed subset D for which supD exists, supD
$U = {\uparrow}U$
and for any directed subset D for which supD exists, supD
![]() $\in U$
implies
$\in U$
implies
![]() $D\cap U \neq \emptyset$
. Correspondingly,
$D\cap U \neq \emptyset$
. Correspondingly,
![]() $A\subseteq P$
is Scott closed if A =
$A\subseteq P$
is Scott closed if A =
![]() $\downarrow$
A and for any directed subset D of P contained in A, supD
$\downarrow$
A and for any directed subset D of P contained in A, supD
![]() $\in A$
when
$\in A$
when
![]() $\sup D$
exists. Until it is otherwise stated, we always equip posets with the Scott topology, and
$\sup D$
exists. Until it is otherwise stated, we always equip posets with the Scott topology, and
![]() $cl_{\sigma}(A)$
or
$cl_{\sigma}(A)$
or
![]() $\overline A$
is used to denote the closure of
$\overline A$
is used to denote the closure of
![]() $A\subseteq P$
with respect to the Scott topology.
$A\subseteq P$
with respect to the Scott topology.
For a
![]() $T_{0}$
topological space X, the partial order
$T_{0}$
topological space X, the partial order
![]() $\leq$
$\leq$
![]() $_{X}$
, defined by
$_{X}$
, defined by
![]() $x\leq y$
iff x is contained in the closure of y, is called the specialization order. We have that for any
$x\leq y$
iff x is contained in the closure of y, is called the specialization order. We have that for any
![]() $x\in X$
,
$x\in X$
,
![]() $\downarrow$
x =
$\downarrow$
x =
![]() $cl(\{x\})$
and a continuous map f between two
$cl(\{x\})$
and a continuous map f between two
![]() $T_{0}$
spaces is always order-preserving. X is called a monotone convergence space (or a d-space) if every subset D directed relative to the specialization order has a supremum, and the relation
$T_{0}$
spaces is always order-preserving. X is called a monotone convergence space (or a d-space) if every subset D directed relative to the specialization order has a supremum, and the relation
![]() $\sup D\in U$
for any open set U of X implies
$\sup D\in U$
for any open set U of X implies
![]() $D\cap U \neq \emptyset$
. Let C(X) denote the set of all closed subsets of X. The lower Vietoris topology on C(X) is the topology generated by
$D\cap U \neq \emptyset$
. Let C(X) denote the set of all closed subsets of X. The lower Vietoris topology on C(X) is the topology generated by
![]() $\{\lozenge U: U\in \mathcal{O}(X)\}$
as a subbase, where
$\{\lozenge U: U\in \mathcal{O}(X)\}$
as a subbase, where
![]() $\lozenge U = \{A\in C(X): A\cap U\neq \emptyset\}$
, and the resulting space denoted by
$\lozenge U = \{A\in C(X): A\cap U\neq \emptyset\}$
, and the resulting space denoted by
![]() $\mathcal H_t(X)$
is called the Hoare power space, here t in the subscript refers to the fact that the construction acts on topological spaces.
$\mathcal H_t(X)$
is called the Hoare power space, here t in the subscript refers to the fact that the construction acts on topological spaces.
![]() $A\in C(X)$
is called irreducible if for any
$A\in C(X)$
is called irreducible if for any
![]() $B, C\in C(X)$
,
$B, C\in C(X)$
,
![]() $A\subseteq B\cup C$
implies that
$A\subseteq B\cup C$
implies that
![]() $A\subseteq B$
or
$A\subseteq B$
or
![]() $A\subseteq C$
. X is called sober if every nonempty irreducible closed set is the closure of a point. From Gierz et al. (Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Exercise V-4.9) we know that there is a sobrification
$A\subseteq C$
. X is called sober if every nonempty irreducible closed set is the closure of a point. From Gierz et al. (Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Exercise V-4.9) we know that there is a sobrification
![]() $(\mathbb S(X), s_X)$
for each
$(\mathbb S(X), s_X)$
for each
![]() $T_0$
space X, where the standard construction for the sobrification is to set
$T_0$
space X, where the standard construction for the sobrification is to set
topologized by open sets
![]() $U^{s} := \{A\in \mathbb S(X): A\cap U\neq\emptyset\}$
for each open subset U of X and
$U^{s} := \{A\in \mathbb S(X): A\cap U\neq\emptyset\}$
for each open subset U of X and
![]() $s_X$
is a topological embedding from X to
$s_X$
is a topological embedding from X to
![]() $\mathbb S(X)$
defined by
$\mathbb S(X)$
defined by
![]() $s_X(x) = cl(\{x\})$
for each
$s_X(x) = cl(\{x\})$
for each
![]() $x\in X$
. We call it standard sobrification.
$x\in X$
. We call it standard sobrification.
For a general full subcategory
![]() $\mathbf K$
of a category
$\mathbf K$
of a category
![]() $\mathbf{C}$
,
$\mathbf{C}$
,
![]() $\mathbf K$
is called reflective if the inclusion functor has a left adjoint, which is then called a reflector and exhibited in the following
$\mathbf K$
is called reflective if the inclusion functor has a left adjoint, which is then called a reflector and exhibited in the following
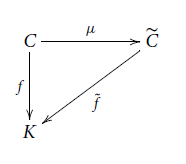
Definition 2.1. (Keimel and Lawson Reference Keimel and Lawson2009) A morphism
![]() $\mu: C\rightarrow \widetilde{C}$
of an object C in
$\mu: C\rightarrow \widetilde{C}$
of an object C in
![]() $\mathbf C$
to an object
$\mathbf C$
to an object
![]() $\widetilde{C}$
is called a universal
$\widetilde{C}$
is called a universal
![]() $\mathbf K$
-ification if it satisfies the following universal property:
$\mathbf K$
-ification if it satisfies the following universal property:
For every object K in
![]() $\mathbf K$
and every map
$\mathbf K$
and every map
![]() $f: C\rightarrow K$
in
$f: C\rightarrow K$
in
![]() $\mathbf C$
, there is a unique morphism
$\mathbf C$
, there is a unique morphism
![]() $\tilde{f}: \widetilde{C}\rightarrow K$
in
$\tilde{f}: \widetilde{C}\rightarrow K$
in
![]() $\mathbf K$
such that
$\mathbf K$
such that
![]() $\tilde{f}\circ\mu = f$
:
$\tilde{f}\circ\mu = f$
:
We call
![]() $\widetilde{C}$
together with the universal
$\widetilde{C}$
together with the universal
![]() $\mathbf K$
-ification
$\mathbf K$
-ification
![]() $\mu$
a
$\mu$
a
![]() $\mathbf K$
-ification of C. It was Keimel and Lawson who first showed that a full subcategory
$\mathbf K$
-ification of C. It was Keimel and Lawson who first showed that a full subcategory
![]() $\mathbf K$
is reflective in
$\mathbf K$
is reflective in
![]() $\mathbf{TOP}_{\mathbf{0}}$
if it satisfies
$\mathbf{TOP}_{\mathbf{0}}$
if it satisfies
![]() $(K_1)$
to
$(K_1)$
to
![]() $(K_4)$
mentioned in the Introduction. In this sense of universal
$(K_4)$
mentioned in the Introduction. In this sense of universal
![]() $\mathbf K$
-ifications, Xu in (2020) provided another approach to constructing
$\mathbf K$
-ifications, Xu in (2020) provided another approach to constructing
![]() $\mathbf K$
-ifications of
$\mathbf K$
-ifications of
![]() $T_0$
spaces.
$T_0$
spaces.
Definition 2.2 (Xu Reference Xu2020). Fix a subcategory
![]() $\mathbf K$
of
$\mathbf K$
of
![]() $\mathbf{TOP}_{\mathbf{0}}$
that satisfies
$\mathbf{TOP}_{\mathbf{0}}$
that satisfies
![]() $(K_2)$
. A subset A of a
$(K_2)$
. A subset A of a
![]() $T_{0}$
space X is called a
$T_{0}$
space X is called a
![]() $\mathbf{K}$
-set, provided for any continuous map
$\mathbf{K}$
-set, provided for any continuous map
![]() $f: X\rightarrow Y$
to a
$f: X\rightarrow Y$
to a
![]() $\mathbf{K}$
-space Y (i.e., Y is an object in
$\mathbf{K}$
-space Y (i.e., Y is an object in
![]() $\mathbf K$
), there exists a unique
$\mathbf K$
), there exists a unique
![]() $y_{A}\in Y$
such that cl(f(A))=
$y_{A}\in Y$
such that cl(f(A))=
![]() $cl(\{y_{A}\})$
. Denote by
$cl(\{y_{A}\})$
. Denote by
![]() $\mathbf{K}(X)$
the set of all closed
$\mathbf{K}(X)$
the set of all closed
![]() $\mathbf{K}$
-sets of X.
$\mathbf{K}$
-sets of X.
In Xu (Reference Xu2020), Xu called a full subcategory
![]() $\mathbf K$
of
$\mathbf K$
of
![]() $\mathbf{TOP}_{\mathbf{0}}$
adequate if for any
$\mathbf{TOP}_{\mathbf{0}}$
adequate if for any
![]() $T_{0}$
space X,
$T_{0}$
space X,
![]() $\mathcal{K}(X)$
, the space obtained by endowing
$\mathcal{K}(X)$
, the space obtained by endowing
![]() $\mathbf{K}(X)$
with the lower Vietoris topology, is a
$\mathbf{K}(X)$
with the lower Vietoris topology, is a
![]() $\mathbf{K}$
-space. He proved that when
$\mathbf{K}$
-space. He proved that when
![]() $\mathbf K$
satisfies
$\mathbf K$
satisfies
![]() $(K_2)$
and is adequate, the pair
$(K_2)$
and is adequate, the pair
![]() $\langle \mathcal{K}(X), \zeta_{X} \rangle$
, where
$\langle \mathcal{K}(X), \zeta_{X} \rangle$
, where
![]() $\zeta_{X}: X\rightarrow \mathcal K(X): x\mapsto cl(\{x\})$
, is a
$\zeta_{X}: X\rightarrow \mathcal K(X): x\mapsto cl(\{x\})$
, is a
![]() $\mathbf{K}$
-ification of X.
$\mathbf{K}$
-ification of X.
Recently, Ershov called a full subcategory
![]() $\mathbf K$
of
$\mathbf K$
of
![]() $\mathbf{TOP}_{\mathbf{0}}$
wide if for any
$\mathbf{TOP}_{\mathbf{0}}$
wide if for any
![]() $T_0$
space X there exists an extension
$T_0$
space X there exists an extension
![]() $Y\geq X$
such that
$Y\geq X$
such that
![]() $Y\in \mathbf K$
. For a wide category
$Y\in \mathbf K$
. For a wide category
![]() $\mathbf K$
, he endowed new definitions for
$\mathbf K$
, he endowed new definitions for
![]() $\mathbf K$
-subspaces and
$\mathbf K$
-subspaces and
![]() $\mathbf K$
-completions and used them to offer sufficient conditions for the existence of
$\mathbf K$
-completions and used them to offer sufficient conditions for the existence of
![]() $\mathbf K$
-ification of an arbitrary
$\mathbf K$
-ification of an arbitrary
![]() $T_0$
space (Ershov Reference Ershov2022).
$T_0$
space (Ershov Reference Ershov2022).
Definition 2.3 (Ershov Reference Ershov2022). Let
![]() $\mathbf K$
be a wide subcategory of
$\mathbf K$
be a wide subcategory of
![]() $\mathbf{TOP}_{\mathbf{0}}$
. We say that a continuous map
$\mathbf{TOP}_{\mathbf{0}}$
. We say that a continuous map
![]() $f: X\rightarrow Y$
between two
$f: X\rightarrow Y$
between two
![]() $T_0$
spaces is
$T_0$
spaces is
![]() $\mathbf K$
-precomplete if for the inclusion functor
$\mathbf K$
-precomplete if for the inclusion functor
![]() $i: \mathbf K\hookrightarrow \mathbf{Top}_{\mathbf{0}}$
, the natural transformation
$i: \mathbf K\hookrightarrow \mathbf{Top}_{\mathbf{0}}$
, the natural transformation
![]() $({-}) \circ f : \mathbf{Top}_{\mathbf{0}} (Y, i({-})) \rightarrow \mathbf{Top}_{\mathbf{0}} (X, i({-}))$
is invertible.
$({-}) \circ f : \mathbf{Top}_{\mathbf{0}} (Y, i({-})) \rightarrow \mathbf{Top}_{\mathbf{0}} (X, i({-}))$
is invertible.
Definition 2.4 (Ershov Reference Ershov2022). Let
![]() $\mathbf K$
be a wide category. An arbitrary subspace
$\mathbf K$
be a wide category. An arbitrary subspace
![]() $Z\leq \mathbb S(X)$
containing X, for which the natural embedding
$Z\leq \mathbb S(X)$
containing X, for which the natural embedding
![]() $s_X: X\rightarrow Z$
is
$s_X: X\rightarrow Z$
is
![]() $\mathbf K$
-precomplete, is called a
$\mathbf K$
-precomplete, is called a
![]() $\mathbf K$
-subspace for X.
$\mathbf K$
-subspace for X.
Ershov denoted by
![]() $X^{\mathbf K}$
the greatest
$X^{\mathbf K}$
the greatest
![]() $\mathbf K$
-subspace for X, whose existence is guaranteed by Ershov (Reference Ershov2022, Theorem 2.2). In addition, he called
$\mathbf K$
-subspace for X, whose existence is guaranteed by Ershov (Reference Ershov2022, Theorem 2.2). In addition, he called
![]() $X^{\mathbf K}$
a
$X^{\mathbf K}$
a
![]() $\mathbf K$
-completion of a
$\mathbf K$
-completion of a
![]() $T_0$
space X if
$T_0$
space X if
![]() $X^{\mathbf K}\in \mathbf K$
.
$X^{\mathbf K}\in \mathbf K$
.
Definition 2.5. (Ershov Reference Ershov2022) Let
![]() $\mathbf K$
be a wide category. A functor
$\mathbf K$
be a wide category. A functor
![]() $F: \mathbf{TOP}_{\mathbf{0}}\rightarrow \mathbf{TOP}_{\mathbf{0}}$
together with a natural transformation
$F: \mathbf{TOP}_{\mathbf{0}}\rightarrow \mathbf{TOP}_{\mathbf{0}}$
together with a natural transformation
![]() $\eta: Id\rightarrow F$
is called a
$\eta: Id\rightarrow F$
is called a
![]() $\mathbf K$
-precompletion if the map
$\mathbf K$
-precompletion if the map
![]() $\eta_X: X\rightarrow F(X)$
is
$\eta_X: X\rightarrow F(X)$
is
![]() $\mathbf K$
-precomplete for any
$\mathbf K$
-precomplete for any
![]() $T_0$
space X.
$T_0$
space X.
A
![]() $\mathbf K$
-precompletion
$\mathbf K$
-precompletion
![]() $(F, \eta)$
is referred to as ample if, for any
$(F, \eta)$
is referred to as ample if, for any
![]() $T_0$
space X, the fact that
$T_0$
space X, the fact that
![]() $\eta_X: X\rightarrow F(X)$
is an identity map implies the inclusion
$\eta_X: X\rightarrow F(X)$
is an identity map implies the inclusion
![]() $X\in \mathbf K$
.
$X\in \mathbf K$
.
Ershov has proved that for a wide category
![]() $\mathbf K$
, the existence of an ample
$\mathbf K$
, the existence of an ample
![]() $\mathbf K$
-precompletion guarantees the existence of the
$\mathbf K$
-precompletion guarantees the existence of the
![]() $\mathbf K$
-completion of an arbitrary
$\mathbf K$
-completion of an arbitrary
![]() $T_0$
space X (Ershov Reference Ershov2022, Theorem 4.3), in other words, he provided a sufficient condition to make the category
$T_0$
space X (Ershov Reference Ershov2022, Theorem 4.3), in other words, he provided a sufficient condition to make the category
![]() $\mathbf K$
reflective in
$\mathbf K$
reflective in
![]() $\mathbf{TOP}_{\mathbf{0}}$
. Next we will show that this condition is also necessary.
$\mathbf{TOP}_{\mathbf{0}}$
. Next we will show that this condition is also necessary.
Proposition 2.6. Let
![]() $\mathbf K$
be a wide category. Then, the
$\mathbf K$
be a wide category. Then, the
![]() $\mathbf K$
-completion exists for each
$\mathbf K$
-completion exists for each
![]() $T_0$
space X if and only if there is an ample
$T_0$
space X if and only if there is an ample
![]() $\mathbf K$
-precompletion
$\mathbf K$
-precompletion
![]() $(F, \eta)$
.
$(F, \eta)$
.
Proof. “If” is clear from Ershov (Reference Ershov2022, Theorem 4.3). Now assume that the
![]() $\mathbf K$
-completion exists for each
$\mathbf K$
-completion exists for each
![]() $T_0$
space X, i.e.,
$T_0$
space X, i.e.,
![]() $X^{\mathbf K}\in \mathbf K$
. Define
$X^{\mathbf K}\in \mathbf K$
. Define
![]() $F: \mathbf{TOP}_{\mathbf{0}}\rightarrow \mathbf{TOP}_{\mathbf{0}}$
as the form of Ershov (Reference Ershov2022, Theorem 3.7) and
$F: \mathbf{TOP}_{\mathbf{0}}\rightarrow \mathbf{TOP}_{\mathbf{0}}$
as the form of Ershov (Reference Ershov2022, Theorem 3.7) and
![]() $\eta_X: X\rightarrow F(X) = X^{\mathbf K}$
as
$\eta_X: X\rightarrow F(X) = X^{\mathbf K}$
as
![]() $s_X$
. Since
$s_X$
. Since
![]() $X^{\mathbf K}$
is a
$X^{\mathbf K}$
is a
![]() $\mathbf K$
-subspace of X,
$\mathbf K$
-subspace of X,
![]() $s_X$
is
$s_X$
is
![]() $\mathbf K$
-precomplete, so is
$\mathbf K$
-precomplete, so is
![]() $\eta_X$
. If
$\eta_X$
. If
![]() $\eta_X$
is an identity map, i.e.,
$\eta_X$
is an identity map, i.e.,
![]() $X\cong X^{\mathbf K}$
, then from Ershov (Reference Ershov2022, Theorem 3.8), we know the existence of
$X\cong X^{\mathbf K}$
, then from Ershov (Reference Ershov2022, Theorem 3.8), we know the existence of
![]() $\mathbf K$
-completions indicates that
$\mathbf K$
-completions indicates that
![]() $(K_1)$
is satisfied. So
$(K_1)$
is satisfied. So
![]() $X^{\mathbf K}\in \mathbf K$
implies
$X^{\mathbf K}\in \mathbf K$
implies
![]() $X\in \mathbf K$
. Hence,
$X\in \mathbf K$
. Hence,
![]() $(F, \eta)$
is an ample
$(F, \eta)$
is an ample
![]() $\mathbf K$
-precompletion.
$\mathbf K$
-precompletion.
Lemma 2.7 (Xu Reference Xu2020). Let
![]() $\mathbf{K}$
be a subcategory of
$\mathbf{K}$
be a subcategory of
![]() $\mathbf{TOP}_{\mathbf{0}}$
that satisfies
$\mathbf{TOP}_{\mathbf{0}}$
that satisfies
![]() $(K_1)$
and
$(K_1)$
and
![]() $(K_2)$
. If it is adequate, then the following conditions are equivalent for each
$(K_2)$
. If it is adequate, then the following conditions are equivalent for each
![]() $T_{0}$
space X:
$T_{0}$
space X:
-
(1) X is a
 $\mathbf{K}$
-space.
$\mathbf{K}$
-space. -
(2)
 $\mathbf{K}(X)$
=
$\mathbf{K}(X)$
=
 $\{{\downarrow}x: x\in X\}$
, that is, for each
$\{{\downarrow}x: x\in X\}$
, that is, for each
 $A\in\mathbf{K}(X)$
, there exists an
$A\in\mathbf{K}(X)$
, there exists an
 $x\in X$
such that A =
$x\in X$
such that A =
 $cl(\{x\})$
.
$cl(\{x\})$
.
Lemma 2.8.
Let Y be a
![]() $T_{0}$
space and X a subspace of Y. If
$T_{0}$
space and X a subspace of Y. If
![]() $A\subseteq X$
, then
$A\subseteq X$
, then
![]() $cl_{Y}(cl_{X}(A)) = cl_{Y}(A)$
.
$cl_{Y}(cl_{X}(A)) = cl_{Y}(A)$
.
Proof. It is clear that
![]() $cl_{X}(A) = cl_{Y}(A)$
for any
$cl_{X}(A) = cl_{Y}(A)$
for any
![]() $A\subseteq X$
. So
$A\subseteq X$
. So
![]() $cl_{Y}(cl_{X}(A)) = cl_{Y}(A)$
.
$cl_{Y}(cl_{X}(A)) = cl_{Y}(A)$
.
Proposition 2.9. If
![]() $\mathbf K$
is a subcategory of
$\mathbf K$
is a subcategory of
![]() $\mathbf{TOP}_{\mathbf{0}}$
satisfying the property
$\mathbf{TOP}_{\mathbf{0}}$
satisfying the property
![]() $(K_{2})$
, then it satisfies properties
$(K_{2})$
, then it satisfies properties
![]() $(K_{1})$
to
$(K_{1})$
to
![]() $(K_{4})$
if and only if it is closed and adequate.
$(K_{4})$
if and only if it is closed and adequate.
Proof. Theorem 5.17 in Xu (Reference Xu2020) told us each subcategory satisfying
![]() $(K_{1})$
to
$(K_{1})$
to
![]() $(K_{4})$
is adequate. Thus, we just need to prove the reverse; that is,
$(K_{4})$
is adequate. Thus, we just need to prove the reverse; that is,
![]() $\mathbf K$
satisfies (
$\mathbf K$
satisfies (
![]() $K_{3}$
) and (
$K_{3}$
) and (
![]() $K_{4}$
) if it is closed and adequate.
$K_{4}$
) if it is closed and adequate.
For (
![]() $K_{3}$
), let
$K_{3}$
), let
![]() $\{X_{i}: i\in I\}$
be a family of
$\{X_{i}: i\in I\}$
be a family of
![]() $\mathbf{K}$
-subspaces of S, where
$\mathbf{K}$
-subspaces of S, where
![]() $\mathbf K$
-subspaces mentioned in
$\mathbf K$
-subspaces mentioned in
![]() $(K_3)$
are subspaces of S that are
$(K_3)$
are subspaces of S that are
![]() $\mathbf K$
-spaces in the relative topology. Suppose
$\mathbf K$
-spaces in the relative topology. Suppose
![]() $A\subseteq\bigcap_{i\in I}X_{i}$
is a
$A\subseteq\bigcap_{i\in I}X_{i}$
is a
![]() $\mathbf{K}$
-set. Then, A is a
$\mathbf{K}$
-set. Then, A is a
![]() $\mathbf{K}$
-set of S, which implies that
$\mathbf{K}$
-set of S, which implies that
![]() $cl_{S}(A) = cl_{S}(\{a\})$
for some
$cl_{S}(A) = cl_{S}(\{a\})$
for some
![]() $a\in S$
since the sober space S is a
$a\in S$
since the sober space S is a
![]() $\mathbf{K}$
-space. Meanwhile, A is also a
$\mathbf{K}$
-space. Meanwhile, A is also a
![]() $\mathbf{K}$
-set of every
$\mathbf{K}$
-set of every
![]() $\mathbf{K}$
-space
$\mathbf{K}$
-space
![]() $X_{i}$
; thus, there is an
$X_{i}$
; thus, there is an
![]() $a_{i}\in X_{i}$
such that
$a_{i}\in X_{i}$
such that
![]() $cl_{X_{i}}(A) = cl_{X_{i}}(\{a_{i}\})$
. By Lemma 2.8, we have
$cl_{X_{i}}(A) = cl_{X_{i}}(\{a_{i}\})$
. By Lemma 2.8, we have
![]() $cl_{S}(cl_{X_{i}}(A)) = cl_{S}(A)$
, which means
$cl_{S}(cl_{X_{i}}(A)) = cl_{S}(A)$
, which means
![]() $cl_{S}(cl_{X_{i}}(\{a_{i}\})) = cl_{S}(\{a\})$
. By the fact that
$cl_{S}(cl_{X_{i}}(\{a_{i}\})) = cl_{S}(\{a\})$
. By the fact that
![]() $cl_{S}(cl_{X_{i}}(\{a_{i}\})) = cl_{S}(\{a_{i}\})$
, we have
$cl_{S}(cl_{X_{i}}(\{a_{i}\})) = cl_{S}(\{a_{i}\})$
, we have
![]() $cl_{S}(\{a_{i}\}) = cl_{S}(\{a\})$
. Thus,
$cl_{S}(\{a_{i}\}) = cl_{S}(\{a\})$
. Thus,
![]() $a_{i} = a$
and
$a_{i} = a$
and
![]() $a\in \bigcap_{i\in I}X_{i}$
. Therefore,
$a\in \bigcap_{i\in I}X_{i}$
. Therefore,
![]() $cl_{\bigcap_{i\in I}X_{i}}(A) = cl_{\bigcap_{i\in I}X_{i}}(\{a\})$
. So relying on the adequateness, by Lemma 2.7, we have that
$cl_{\bigcap_{i\in I}X_{i}}(A) = cl_{\bigcap_{i\in I}X_{i}}(\{a\})$
. So relying on the adequateness, by Lemma 2.7, we have that
![]() ${\bigcap_{i\in I}X_{i}}$
is a
${\bigcap_{i\in I}X_{i}}$
is a
![]() $\mathbf{K}$
-space.
$\mathbf{K}$
-space.
For (
![]() $K_{4}$
), let S, T be sober spaces and
$K_{4}$
), let S, T be sober spaces and
![]() $f: S\rightarrow T$
a continuous map. Assume that X is a
$f: S\rightarrow T$
a continuous map. Assume that X is a
![]() $\mathbf{K}$
-subspace of T. For any
$\mathbf{K}$
-subspace of T. For any
![]() $\mathbf{K}$
-set
$\mathbf{K}$
-set
![]() $A\subseteq f^{-1}(X)$
, A is also a
$A\subseteq f^{-1}(X)$
, A is also a
![]() $\mathbf{K}$
-set of S. Then, there is an
$\mathbf{K}$
-set of S. Then, there is an
![]() $a\in S$
such that
$a\in S$
such that
![]() $cl_{S}(A) = cl_{S}(\{a\})$
. Besides, by the continuity of f, we know
$cl_{S}(A) = cl_{S}(\{a\})$
. Besides, by the continuity of f, we know
![]() $f(A)\subseteq X$
is a
$f(A)\subseteq X$
is a
![]() $\mathbf{K}$
-set of T and one can verify that f(A) is also a
$\mathbf{K}$
-set of T and one can verify that f(A) is also a
![]() $\mathbf{K}$
-set of X. Thus there are two points
$\mathbf{K}$
-set of X. Thus there are two points
![]() $a_{1}\in X$
and
$a_{1}\in X$
and
![]() $a_{2}\in T$
such that
$a_{2}\in T$
such that
![]() $cl_{X}(f(A)) = cl_{X}(\{a_{1}\})$
and
$cl_{X}(f(A)) = cl_{X}(\{a_{1}\})$
and
![]() $cl_{T}(f(A)) = cl_{T}(\{a_{2}\})$
, respectively. By Lemma 2.8,
$cl_{T}(f(A)) = cl_{T}(\{a_{2}\})$
, respectively. By Lemma 2.8,
![]() $cl_{T}(cl_{X}(f(A))) = cl_{T}(f(A))$
, thus
$cl_{T}(cl_{X}(f(A))) = cl_{T}(f(A))$
, thus
![]() $a_{1} = a_{2}$
. Now we have
$a_{1} = a_{2}$
. Now we have
![]() $f(a) = f(\sup_{S} A) = \sup_{T}f(A) = a_{2}$
. As
$f(a) = f(\sup_{S} A) = \sup_{T}f(A) = a_{2}$
. As
![]() $a_{1} = a_{2}$
and
$a_{1} = a_{2}$
and
![]() $a_{1}\in X$
,
$a_{1}\in X$
,
![]() $f(a)\in X$
, that is,
$f(a)\in X$
, that is,
![]() $\sup_{S} A = a\in f^{-1}(X)$
. This means
$\sup_{S} A = a\in f^{-1}(X)$
. This means
![]() $\sup_{f^{-1}(X)}A$
exists and equals to
$\sup_{f^{-1}(X)}A$
exists and equals to
![]() $\sup_{S} A$
. Thus,
$\sup_{S} A$
. Thus,
![]() $cl_{f^{-1}(X)}(A) = cl_{f^{-1}(X)}(\{\sup_{f^{-1}(X)}A \}) = cl_{f^{-1}(X)}(\{\sup_{S}A\}) = cl_{f^{-1}(X)}(\{a\})$
. Therefore, using the adequateness and Lemma 2.7 again, we have that
$cl_{f^{-1}(X)}(A) = cl_{f^{-1}(X)}(\{\sup_{f^{-1}(X)}A \}) = cl_{f^{-1}(X)}(\{\sup_{S}A\}) = cl_{f^{-1}(X)}(\{a\})$
. Therefore, using the adequateness and Lemma 2.7 again, we have that
![]() $f^{-1}(X)$
is a
$f^{-1}(X)$
is a
![]() $\mathbf{K}$
-subspace of S.
$\mathbf{K}$
-subspace of S.
Given that Ershov has shown that a full subcategory
![]() $\mathbf K$
of
$\mathbf K$
of
![]() $\mathbf{TOP}_{\mathbf{0}}$
satisfies the properties
$\mathbf{TOP}_{\mathbf{0}}$
satisfies the properties
![]() $(K_1)$
to
$(K_1)$
to
![]() $(K_4)$
if and only if
$(K_4)$
if and only if
![]() $\mathbf K$
is wide and
$\mathbf K$
is wide and
![]() $\mathbf K$
-completion exists for each
$\mathbf K$
-completion exists for each
![]() $T_0$
space (see Ershov Reference Ershov2022, Theorem 3.8), then together with Propositions 2.6 and 2.9, we could draw the following conclusion.
$T_0$
space (see Ershov Reference Ershov2022, Theorem 3.8), then together with Propositions 2.6 and 2.9, we could draw the following conclusion.
Theorem 2.10. Let
![]() $\mathbf K$
be a full subcategory of
$\mathbf K$
be a full subcategory of
![]() $\mathbf{TOP}_{\mathbf{0}}$
. Then, the following statements are equivalent.
$\mathbf{TOP}_{\mathbf{0}}$
. Then, the following statements are equivalent.
-
(1)
 $\mathbf K$
is a wide category and there exists an ample
$\mathbf K$
is a wide category and there exists an ample
 $\mathbf K$
-precompletion
$\mathbf K$
-precompletion
 $(F, \eta)$
on the category
$(F, \eta)$
on the category
 $\mathbf{TOP}_{\mathbf{0}}$
.
$\mathbf{TOP}_{\mathbf{0}}$
. -
(2)
 $\mathbf K$
satisfies the properties
$\mathbf K$
satisfies the properties
 $(K_1)$
-
$(K_1)$
-
 $(K_4)$
.
$(K_4)$
. -
(3)
 $\mathbf K$
satisfies the properties
$\mathbf K$
satisfies the properties
 $(K_1)$
,
$(K_1)$
,
 $(K_2)$
and is adequate.
$(K_2)$
and is adequate.
It can be seen from the above theorem that the
![]() $\mathbf K$
-ifications of a
$\mathbf K$
-ifications of a
![]() $T_0$
space constructed by Keimel and Lawson, Xu, and Ershov respectively are consistent. In our paper, we will mainly use Xu’s description for
$T_0$
space constructed by Keimel and Lawson, Xu, and Ershov respectively are consistent. In our paper, we will mainly use Xu’s description for
![]() $\mathbf K$
-ifications. This is because, when constructing an order-
$\mathbf K$
-ifications. This is because, when constructing an order-
![]() $\mathbf K$
-ification monad on DCPO and further examining its algebras, it benefits us a lot if we know concretely what composes such a completion.
$\mathbf K$
-ification monad on DCPO and further examining its algebras, it benefits us a lot if we know concretely what composes such a completion.
3. Categories of Type
 $\mathrm K^*$
$\mathrm K^*$
In what follows, a category of type
![]() $\mathrm K$
is defined by satisfying Properties
$\mathrm K$
is defined by satisfying Properties
![]() $(K_1)$
,
$(K_1)$
,
![]() $(K_2)$
mentioned in the Introduction and the adequacy property. Categories of type
$(K_2)$
mentioned in the Introduction and the adequacy property. Categories of type
![]() $\mathrm K$
were initially considered by Keimel and Lawson in (2009), and they are also called K-categories in Jia and Mislove (Reference Jia and Mislove2022).
$\mathrm K$
were initially considered by Keimel and Lawson in (2009), and they are also called K-categories in Jia and Mislove (Reference Jia and Mislove2022).
Definition 3.1. A full subcategory of
![]() $\mathbf{TOP}_{\mathbf{0}}$
of type
$\mathbf{TOP}_{\mathbf{0}}$
of type
![]() $\mathrm K$
is said to be of type
$\mathrm K$
is said to be of type
![]() $\mathrm{K}^{*}$
if its objects, called
$\mathrm{K}^{*}$
if its objects, called
![]() $\mathbf K^*$
-spaces, also satisfy the following property:
$\mathbf K^*$
-spaces, also satisfy the following property:
(
![]() $K_5$
) All
$K_5$
) All
![]() $\mathbf K^*$
-spaces are monotone convergence spaces.
$\mathbf K^*$
-spaces are monotone convergence spaces.
Remark 3.2. Given a category of type
![]() $\mathrm K$
, the full subcategory of all monotone convergence
$\mathrm K$
, the full subcategory of all monotone convergence
![]() $\mathbf K$
-spaces, denoted by
$\mathbf K$
-spaces, denoted by
![]() $\mathbf K^{*}$
, is of type
$\mathbf K^{*}$
, is of type
![]() $\mathrm K^{*}$
. In the following, the category
$\mathrm K^{*}$
. In the following, the category
![]() $\mathbf K^{*}$
is always constructed in this way from a category
$\mathbf K^{*}$
is always constructed in this way from a category
![]() $\mathbf K$
of type
$\mathbf K$
of type
![]() $\mathrm K$
.
$\mathrm K$
.
Example 3.3.
SOB and MCS have been shown to be categories of type
![]() $\mathrm K^{*}$
in Gierz et al. (Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003), Keimel and Lawson (Reference Keimel and Lawson2009). Wu et al. proved that WF of all well-filtered spaces and continuous maps satisfies the properties
$\mathrm K^{*}$
in Gierz et al. (Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003), Keimel and Lawson (Reference Keimel and Lawson2009). Wu et al. proved that WF of all well-filtered spaces and continuous maps satisfies the properties
![]() $(K_1)$
to
$(K_1)$
to
![]() $(K_4)$
and thus a category of type K (Wu et al. Reference Wu, Xi, Xu and Zhao2020). As Xi and Lawson in Xi nad Lawson (2017) illustrated that each well-filtered space is a monotone convergence space, WF is also a category of type
$(K_4)$
and thus a category of type K (Wu et al. Reference Wu, Xi, Xu and Zhao2020). As Xi and Lawson in Xi nad Lawson (2017) illustrated that each well-filtered space is a monotone convergence space, WF is also a category of type
![]() $\mathrm K^{*}$
, which lies between SOB and MCS.
$\mathrm K^{*}$
, which lies between SOB and MCS.
The following example distinguishes the category of type
![]() $\mathrm{K}^{*}$
from that of type K.
$\mathrm{K}^{*}$
from that of type K.
Example 3.4. In Xu et al. (Reference Xu, Shen, Xi and Zhao2020), Xu introduced the
![]() $\omega$
-well-filtered spaces and illustrated that an
$\omega$
-well-filtered spaces and illustrated that an
![]() $\omega$
-well-filtered space may not be a monotone convergence space. The reader is referred to Xu et al. (Reference Xu, Shen, Xi and Zhao2020, Example 4.3) for details. It was proved that the category
$\omega$
-well-filtered space may not be a monotone convergence space. The reader is referred to Xu et al. (Reference Xu, Shen, Xi and Zhao2020, Example 4.3) for details. It was proved that the category
![]() $\omega$
-
$\omega$
-
![]() $\mathbf{WF}$
of all
$\mathbf{WF}$
of all
![]() $\omega$
-well-filtered spaces and continuous maps is reflective in
$\omega$
-well-filtered spaces and continuous maps is reflective in
![]() $\mathbf{TOP}_{\mathbf{0}}$
, which indicates that
$\mathbf{TOP}_{\mathbf{0}}$
, which indicates that
![]() $\omega$
-
$\omega$
-
![]() $\mathbf{WF}$
satisfies the properties
$\mathbf{WF}$
satisfies the properties
![]() $(K_1)$
to
$(K_1)$
to
![]() $(K_4)$
by Shen et al. (Reference Shen, Xi and Zhao2021, Theorem 2.16). So
$(K_4)$
by Shen et al. (Reference Shen, Xi and Zhao2021, Theorem 2.16). So
![]() $\omega$
-
$\omega$
-
![]() $\mathbf{WF}$
is of type K, but not of type
$\mathbf{WF}$
is of type K, but not of type
![]() $\mathrm{K}^{*}$
.
$\mathrm{K}^{*}$
.
Definition 3.5. Let X be a
![]() $T_{0}$
space.
$T_{0}$
space.
![]() $A\subseteq X$
is a
$A\subseteq X$
is a
![]() $\mathbf{K}^{*}$
-set if for any
$\mathbf{K}^{*}$
-set if for any
![]() $\mathbf{K}^{*}$
-space Y and any continuous map
$\mathbf{K}^{*}$
-space Y and any continuous map
![]() $f: X\rightarrow Y$
, there exists a unique element
$f: X\rightarrow Y$
, there exists a unique element
![]() $y_{0}\in Y$
such that cl(f(A)) =
$y_{0}\in Y$
such that cl(f(A)) =
![]() $cl(\{y_{0}\})$
.
$cl(\{y_{0}\})$
.
Let
![]() $\mathbf{K}^{*}(X)$
denote the set of all closed
$\mathbf{K}^{*}(X)$
denote the set of all closed
![]() $\mathbf{K}^{*}$
-sets of X. Then, A is a
$\mathbf{K}^{*}$
-sets of X. Then, A is a
![]() $\mathbf{K}^{*}$
-set iff
$\mathbf{K}^{*}$
-set iff
![]() $cl(A)\in \mathbf{K}^{*}(X)$
. In particular, when
$cl(A)\in \mathbf{K}^{*}(X)$
. In particular, when
![]() $\mathbf{K}^{*}$
is SOB or WF, a
$\mathbf{K}^{*}$
is SOB or WF, a
![]() $\mathbf{K}^{*}$
-set of a
$\mathbf{K}^{*}$
-set of a
![]() $T_{0}$
space X is indeed an irreducible set or a well-filtered determined set defined by Xu in Xu and Zhao (Reference Xu and Zhao2020), respectively. We will use
$T_{0}$
space X is indeed an irreducible set or a well-filtered determined set defined by Xu in Xu and Zhao (Reference Xu and Zhao2020), respectively. We will use
![]() $\mathbf{WF}(X)$
to denote the family consisting of all closed well-filtered determined sets of X.
$\mathbf{WF}(X)$
to denote the family consisting of all closed well-filtered determined sets of X.
Lemma 3.6. Let X, Y be
![]() $T_{0}$
spaces and
$T_{0}$
spaces and
![]() $f: X\rightarrow Y$
a continuous map. If
$f: X\rightarrow Y$
a continuous map. If
![]() $A\subseteq X$
is a
$A\subseteq X$
is a
![]() $\mathbf{K}^{*}$
-set, then f(A) is a
$\mathbf{K}^{*}$
-set, then f(A) is a
![]() $\mathbf{K}^{*}$
-set of Y.
$\mathbf{K}^{*}$
-set of Y.
Proof. The proof is similar to that of Xu (Reference Xu2020, Lemma 3.11).
Definition 3.7 (Zhang and Li Reference Zhang and Li2017). A subset A of a space X is called tapered if for any continuous map
![]() $f:X\rightarrow Y$
with Y a monotone convergence space,
$f:X\rightarrow Y$
with Y a monotone convergence space,
![]() $\sup f(A)$
always exists in Y.
$\sup f(A)$
always exists in Y.
Lemma 3.8 (Zhang and Li Reference Zhang and Li2017). Let X be a monotone convergence space. If
![]() $A\subseteq X$
is tapered and closed, then
$A\subseteq X$
is tapered and closed, then
![]() $A = \ \downarrow\!\!(\bigvee A)$
.
$A = \ \downarrow\!\!(\bigvee A)$
.
Clearly, each directed subset is tapered, which together with the above lemma guarantees the following result:
Lemma 3.9. Let X be a
![]() $T_{0}$
space. Then, the following conditions are equivalent:
$T_{0}$
space. Then, the following conditions are equivalent:
-
(1) X is a monotone convergence space.
-
(2) For any tapered and closed subset
 $A\subseteq X$
,
$A\subseteq X$
,
 $A = cl(\{x_{0}\})$
for some
$A = cl(\{x_{0}\})$
for some
 $x_{0}\in X$
.
$x_{0}\in X$
.
Lemma 3.10.
Let X be a
![]() $T_{0}$
space. Then, we have
$T_{0}$
space. Then, we have
-
(1) Every
 $\mathbf{K}$
-set of X is a
$\mathbf{K}$
-set of X is a
 $\mathbf{K}^{*}$
-set.
$\mathbf{K}^{*}$
-set. -
(2) Every tapered set of X is a
 $\mathbf{K}^{*}$
-set.
$\mathbf{K}^{*}$
-set.
Proof. (1): Let Y be a
![]() $\mathbf{K}^{*}$
-space and
$\mathbf{K}^{*}$
-space and
![]() $f: X\rightarrow Y$
a continuous map. By definition of a
$f: X\rightarrow Y$
a continuous map. By definition of a
![]() $\mathbf{K}^{*}$
-space, we know Y is a K-space; thus for any
$\mathbf{K}^{*}$
-space, we know Y is a K-space; thus for any
![]() $\mathbf{K}$
-set
$\mathbf{K}$
-set
![]() $A\subseteq X$
, there exists a unique element y such that cl(f(A)) =
$A\subseteq X$
, there exists a unique element y such that cl(f(A)) =
![]() $cl(\{y\})$
by Lemma 2.7. It follows that A is a
$cl(\{y\})$
by Lemma 2.7. It follows that A is a
![]() $\mathbf{K}^{*}$
-set.
$\mathbf{K}^{*}$
-set.
(2): Similarly, we can prove that each tapered set is also a
![]() $\mathbf{K}^{*}$
-set by Lemma 3.9.
$\mathbf{K}^{*}$
-set by Lemma 3.9.
Lemma 3.11. For a
![]() $T_{0}$
space X, the following conditions are equivalent:
$T_{0}$
space X, the following conditions are equivalent:
-
(1) X is a
 $\mathbf{{K}}^{*}$
-space.
$\mathbf{{K}}^{*}$
-space. -
(2) For each
 $\mathbf{K}^{*}$
-set
$\mathbf{K}^{*}$
-set
 $A\subseteq X$
, there exists an element
$A\subseteq X$
, there exists an element
 $a_0$
such that
$a_0$
such that
 $cl(A) = cl(\{a_0\})$
.
$cl(A) = cl(\{a_0\})$
.
Proof.
![]() $(1)\Rightarrow(2)$
: Let
$(1)\Rightarrow(2)$
: Let
![]() $id: X\rightarrow X$
be the identity map. Its continuity makes a fact that there is an element
$id: X\rightarrow X$
be the identity map. Its continuity makes a fact that there is an element
![]() $a_0$
such that cl(A) =
$a_0$
such that cl(A) =
![]() $cl(\{a_0\})$
.
$cl(\{a_0\})$
.
![]() $(2)\Rightarrow (1)$
: For any
$(2)\Rightarrow (1)$
: For any
![]() $\mathbf{K}$
-set A of X, by Lemma 3.10, A is a
$\mathbf{K}$
-set A of X, by Lemma 3.10, A is a
![]() $\mathbf{K}^{*}$
-set, thus cl(A) =
$\mathbf{K}^{*}$
-set, thus cl(A) =
![]() $cl(\{a_0\})$
for some
$cl(\{a_0\})$
for some
![]() $a_0\in A$
by (2). So we conclude that X is a
$a_0\in A$
by (2). So we conclude that X is a
![]() $\mathbf{K}$
-space by Lemma 2.7. Similarly, we could show that X is also a monotone convergence space.
$\mathbf{K}$
-space by Lemma 2.7. Similarly, we could show that X is also a monotone convergence space.
Theorem 3.12. Let X be a
![]() $T_{0}$
space. Then,
$T_{0}$
space. Then,
![]() $\mathcal K_{t}(X)$
, i.e.,
$\mathcal K_{t}(X)$
, i.e.,
![]() $\mathbf{K}^{*}(X)$
endowed with the lower Vietoris topology is a
$\mathbf{K}^{*}(X)$
endowed with the lower Vietoris topology is a
![]() $\mathbf{K}^{*}$
-space.
$\mathbf{K}^{*}$
-space.
Proof. Assume that
![]() $\mathcal{A}$
is a closed
$\mathcal{A}$
is a closed
![]() $\mathbf{K}^{*}$
-set of
$\mathbf{K}^{*}$
-set of
![]() $\mathbf{K}^{*}(X)$
. We claim that
$\mathbf{K}^{*}(X)$
. We claim that
![]() $\bigcup\mathcal{A}$
is a
$\bigcup\mathcal{A}$
is a
![]() $\mathbf{K}^{*}$
-set of X. Let Y be a
$\mathbf{K}^{*}$
-set of X. Let Y be a
![]() $\mathbf{K}^{*}$
-space and
$\mathbf{K}^{*}$
-space and
![]() $f: X\rightarrow Y$
a continuous map. Then, define a map
$f: X\rightarrow Y$
a continuous map. Then, define a map
whose rationality is guaranteed by Lemma 3.6. For each open set
![]() $\lozenge U$
of
$\lozenge U$
of
![]() $ \mathbf{K}^{*}(Y)$
, where
$ \mathbf{K}^{*}(Y)$
, where
![]() $U\in \mathcal{O}(Y)$
,
$U\in \mathcal{O}(Y)$
,
![]() $g^{-1}(\lozenge U) = \lozenge f^{-1}(U)$
, so g is continuous. Since each
$g^{-1}(\lozenge U) = \lozenge f^{-1}(U)$
, so g is continuous. Since each
![]() $A\in \mathcal{A}$
belongs to
$A\in \mathcal{A}$
belongs to
![]() $\mathbf{K}^{*}(X)$
, there exists a
$\mathbf{K}^{*}(X)$
, there exists a
![]() $y_{A}\in Y$
such that
$y_{A}\in Y$
such that
![]() $cl(f(A)) = {\downarrow} y_{A}$
. It follows that
$cl(f(A)) = {\downarrow} y_{A}$
. It follows that
![]() $g(\mathcal{A}) = \{{\downarrow} y_{A}: A\in \mathcal{A}\}$
is a
$g(\mathcal{A}) = \{{\downarrow} y_{A}: A\in \mathcal{A}\}$
is a
![]() $\mathbf{K}^{*}$
-set of
$\mathbf{K}^{*}$
-set of
![]() $\mathbf{K}^{*}(Y)$
. As Y is a
$\mathbf{K}^{*}(Y)$
. As Y is a
![]() $\mathbf{K}^{*}$
-space, by Lemma 3.11, we could define a map
$\mathbf{K}^{*}$
-space, by Lemma 3.11, we could define a map
one can easily verify that h is continuous. Then, by Lemma 3.6 again,
![]() $h(\{{\downarrow} y_{A}: A\in \mathcal{A}\}) = \{y_{A}: A\in \mathcal{A}\}$
is a
$h(\{{\downarrow} y_{A}: A\in \mathcal{A}\}) = \{y_{A}: A\in \mathcal{A}\}$
is a
![]() $\mathbf{K}^{*}$
-set of Y. Hence,
$\mathbf{K}^{*}$
-set of Y. Hence,
![]() $\sup\{y_{A}: A\in \mathcal{A}\} = y_{0}$
exists. Then, we have
$\sup\{y_{A}: A\in \mathcal{A}\} = y_{0}$
exists. Then, we have
which entails that
![]() $\bigcup\mathcal{A}$
is a
$\bigcup\mathcal{A}$
is a
![]() $\mathbf{K}^{*}$
-set. So
$\mathbf{K}^{*}$
-set. So
![]() $\mathcal{A} = cl(\{\bigcup\mathcal{A}\})$
and
$\mathcal{A} = cl(\{\bigcup\mathcal{A}\})$
and
![]() $\mathcal K_{t}(X)$
is a
$\mathcal K_{t}(X)$
is a
![]() $\mathbf{K}^{*}$
-space by Lemma 3.11.
$\mathbf{K}^{*}$
-space by Lemma 3.11.
Theorem 3.13. Let X be a
![]() $T_{0}$
space. Then, the pair
$T_{0}$
space. Then, the pair
![]() $(\mathcal K_{t}(X), \eta_{X})$
, where
$(\mathcal K_{t}(X), \eta_{X})$
, where
![]() $\eta_{X}$
:
$\eta_{X}$
:
![]() $X\rightarrow \mathcal K_{t}(X)$
,
$X\rightarrow \mathcal K_{t}(X)$
,
![]() $x\mapsto cl(\{x\})$
, is a
$x\mapsto cl(\{x\})$
, is a
![]() $\mathbf{K}^{*}$
-ification of X.
$\mathbf{K}^{*}$
-ification of X.
Proof. The proof is similar to that of Xu (Reference Xu2020, Theorem 4.6) which proves that
![]() $\langle X^{k} = \mathcal K(X), \zeta_{X}\rangle$
is a
$\langle X^{k} = \mathcal K(X), \zeta_{X}\rangle$
is a
![]() $\mathbf{K}$
-ification of X.
$\mathbf{K}$
-ification of X.
Remark 3.14. (Xu 2020, Theorem 5.14) When a category
![]() $\mathbf{K}^{*}$
of type
$\mathbf{K}^{*}$
of type
![]() $\mathrm K^*$
is specifically taken as WF,
$\mathrm K^*$
is specifically taken as WF,
![]() $\mathcal K_t(X)$
is
$\mathcal K_t(X)$
is
![]() $\mathcal{WF}_t(X)$
, i.e.,
$\mathcal{WF}_t(X)$
, i.e.,
![]() $\mathbf{WF}(X)$
endowed with the lower Vietoris topology, and
$\mathbf{WF}(X)$
endowed with the lower Vietoris topology, and
![]() $\eta_X: X\rightarrow \mathcal{WF}_t(X)$
is defined as
$\eta_X: X\rightarrow \mathcal{WF}_t(X)$
is defined as
Then, (
![]() $\mathcal{WF}_t(X), \eta_X)$
is a well-filtered reflection of X.
$\mathcal{WF}_t(X), \eta_X)$
is a well-filtered reflection of X.
4. The Order-K-ification Monad
A monad on a category C consists of an endofunctor
![]() $\mathcal T$
on C together with natural transformations
$\mathcal T$
on C together with natural transformations
![]() $\eta : Id_{\mathbf C} \rightarrow \mathcal T$
and
$\eta : Id_{\mathbf C} \rightarrow \mathcal T$
and
![]() $\mu: \mathcal T^2 \rightarrow \mathcal T$
such that
$\mu: \mathcal T^2 \rightarrow \mathcal T$
such that
![]() $\mu_{A} \circ \mathcal T\eta_A = Id_{\mathcal TA} = \mu_A \circ \eta_{\mathcal TA}$
and
$\mu_{A} \circ \mathcal T\eta_A = Id_{\mathcal TA} = \mu_A \circ \eta_{\mathcal TA}$
and
![]() $\mu_A \circ \mathcal T\mu_A = \mu_A \circ \mu_{\mathcal TA}$
(Mac Lane Reference Mac Lane1998).
$\mu_A \circ \mathcal T\mu_A = \mu_A \circ \mu_{\mathcal TA}$
(Mac Lane Reference Mac Lane1998).
Let
![]() $\mathbf K^*$
be a category of type
$\mathbf K^*$
be a category of type
![]() $\mathrm K^{*}$
, as in Remark 3.2, determined by certain category of type
$\mathrm K^{*}$
, as in Remark 3.2, determined by certain category of type
![]() $\mathrm K$
. Theorems 3.12 and 3.13 tell us the corresponding reflector
$\mathrm K$
. Theorems 3.12 and 3.13 tell us the corresponding reflector
![]() $\mathcal K_t$
, sending each
$\mathcal K_t$
, sending each
![]() $T_0$
topological space X to its
$T_0$
topological space X to its
![]() $\mathbf{K}^{\mathbf{*}}$
-ification (or the
$\mathbf{K}^{\mathbf{*}}$
-ification (or the
![]() $\mathbf{K}^{\mathbf{*}}$
-space completion), composing the inclusion functor Inc is not only a monad on
$\mathbf{K}^{\mathbf{*}}$
-space completion), composing the inclusion functor Inc is not only a monad on
![]() $\mathbf{TOP}_{\mathbf{0}}$
but can be restricted to
$\mathbf{TOP}_{\mathbf{0}}$
but can be restricted to
![]() $\mathbf {MCS}$
. Now compose them with the pair of functors
$\mathbf {MCS}$
. Now compose them with the pair of functors
![]() $\Omega$
and
$\Omega$
and
![]() $\Sigma$
:
$\Sigma$
:
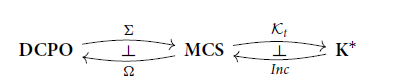
where
![]() $\Sigma$
assigns to each dcpo L the topological space
$\Sigma$
assigns to each dcpo L the topological space
![]() $(L, \sigma (L))$
, and
$(L, \sigma (L))$
, and
![]() $\Omega$
assigns to each monotone convergence space X the dcpo
$\Omega$
assigns to each monotone convergence space X the dcpo
![]() $(X, \leq)$
with
$(X, \leq)$
with
![]() $\leq$
the specialization order on X. We write
$\leq$
the specialization order on X. We write
![]() $\mathcal K_{t}\circ \Sigma$
as
$\mathcal K_{t}\circ \Sigma$
as
![]() $\mathcal K_{d}$
and
$\mathcal K_{d}$
and
![]() $Inc\circ \Omega$
as
$Inc\circ \Omega$
as
![]() $\mathrm {Inc}$
. Then
$\mathrm {Inc}$
. Then
![]() $\mathcal K_{d}$
is left adjoint to
$\mathcal K_{d}$
is left adjoint to
![]() $\mathrm {Inc}$
. By the fact that each adjoint pair determines a monad, one can refer to Borceux (Reference Borceux1994, Proposition 4.2.1), we know the triple
$\mathrm {Inc}$
. By the fact that each adjoint pair determines a monad, one can refer to Borceux (Reference Borceux1994, Proposition 4.2.1), we know the triple
![]() $(\mathrm {Inc}\circ \mathcal K_{d}, \eta, \mathrm{Inc}\circ\varepsilon \circ \mathcal K_{d})$
, where
$(\mathrm {Inc}\circ \mathcal K_{d}, \eta, \mathrm{Inc}\circ\varepsilon \circ \mathcal K_{d})$
, where
![]() $\eta$
and
$\eta$
and
![]() $\varepsilon$
are the unit and counit respectively, turns into a monad on
$\varepsilon$
are the unit and counit respectively, turns into a monad on
![]() $\mathbf{DCPO}$
.
$\mathbf{DCPO}$
.
We denote
![]() $\mathrm{Inc}\circ\mathcal K_{d}$
with
$\mathrm{Inc}\circ\mathcal K_{d}$
with
![]() $\mathcal K$
, for any dcpo L,
$\mathcal K$
, for any dcpo L,
![]() $\mathcal{K}(L)$
is a dcpo consisting of all closed
$\mathcal{K}(L)$
is a dcpo consisting of all closed
![]() $\mathbf{K}^{*}$
-sets of
$\mathbf{K}^{*}$
-sets of
![]() $(L, \sigma(L))$
ordered by set inclusion. For each directed family
$(L, \sigma(L))$
ordered by set inclusion. For each directed family
![]() $\mathcal{C}$
of
$\mathcal{C}$
of
![]() $\mathcal{K}(L)$
, one can verify that
$\mathcal{K}(L)$
, one can verify that
![]() $\bigcup \mathcal{C}$
is a
$\bigcup \mathcal{C}$
is a
![]() $\mathbf{K}^{*}$
-set of L, so the supremum of
$\mathbf{K}^{*}$
-set of L, so the supremum of
![]() $\mathcal{C}$
in
$\mathcal{C}$
in
![]() $\mathcal{K}(L)$
is the Scott closure of
$\mathcal{K}(L)$
is the Scott closure of
![]() $\bigcup \mathcal{C}$
. Meanwhile, we calculate that
$\bigcup \mathcal{C}$
. Meanwhile, we calculate that
![]() $\mathrm{Inc}\circ\varepsilon\circ \mathcal K_{d}$
(replaced by
$\mathrm{Inc}\circ\varepsilon\circ \mathcal K_{d}$
(replaced by
![]() $\mu_{L}$
when it works on a dcpo L) is a natural transformation from
$\mu_{L}$
when it works on a dcpo L) is a natural transformation from
![]() $\mathcal{K}(\mathcal{K}(L))$
to
$\mathcal{K}(\mathcal{K}(L))$
to
![]() $\mathcal{K}(L)$
that maps
$\mathcal{K}(L)$
that maps
![]() $\mathcal{A}$
to
$\mathcal{A}$
to
![]() $\sup_{\mathcal{K}(L)}\mathcal A$
.
$\sup_{\mathcal{K}(L)}\mathcal A$
.
Lemma 4.1. Let L be a dcpo and
![]() $\mathcal{A}$
a Scott closed
$\mathcal{A}$
a Scott closed
![]() $\mathbf K^{*}$
-set of
$\mathbf K^{*}$
-set of
![]() $\mathcal K(L)$
. Then
$\mathcal K(L)$
. Then
![]() $\bigcup\mathcal{A}\in \mathcal{K}(L)$
.
$\bigcup\mathcal{A}\in \mathcal{K}(L)$
.
Proof. The proof of
![]() $\bigcup\mathcal{A}$
being a
$\bigcup\mathcal{A}$
being a
![]() $\mathbf K^{*}$
-set is similar to that in Theorem 3.12 and the Scott closure of
$\mathbf K^{*}$
-set is similar to that in Theorem 3.12 and the Scott closure of
![]() $\bigcup\mathcal{A}$
one can easily verify.
$\bigcup\mathcal{A}$
one can easily verify.
This lemma tells us for each
![]() $\mathcal A\in \mathcal K(\mathcal K(L))$
,
$\mathcal A\in \mathcal K(\mathcal K(L))$
,
![]() $\sup_{\mathcal K(L)}\mathcal{A} = \bigcup\mathcal{A}$
. Now we conclude that
$\sup_{\mathcal K(L)}\mathcal{A} = \bigcup\mathcal{A}$
. Now we conclude that
Theorem 4.2. The endofunctor
![]() $\mathcal{K}$
together with the unit
$\mathcal{K}$
together with the unit
![]() $\eta$
and the multiplication
$\eta$
and the multiplication
![]() $\mu$
forms a monad, called an order-
$\mu$
forms a monad, called an order-
![]() $\mathbf{K}$
-ification monad, on
$\mathbf{K}$
-ification monad, on
![]() $\mathbf{DCPO}$
. Concretely,
$\mathbf{DCPO}$
. Concretely,
![]() $\mathcal{K}$
associates with a dcpo L the dcpo
$\mathcal{K}$
associates with a dcpo L the dcpo
![]() $\mathcal{K}(L)$
and with a morphism
$\mathcal{K}(L)$
and with a morphism
![]() $f: L\longrightarrow M$
in
$f: L\longrightarrow M$
in
![]() $\mathbf{DCPO}$
the map
$\mathbf{DCPO}$
the map
![]() $\mathcal{K}(f)$
:
$\mathcal{K}(f)$
:
![]() $\mathcal{K}(L)\longrightarrow \mathcal{K}(M)$
, which is defined by
$\mathcal{K}(L)\longrightarrow \mathcal{K}(M)$
, which is defined by
![]() $\eta_{L}:L\longrightarrow \mathcal{K}(L)$
and
$\eta_{L}:L\longrightarrow \mathcal{K}(L)$
and
![]() $\mu_{L}: \mathcal{K}(\mathcal{K}(L))\longrightarrow \mathcal{K}(L)$
are defined by
$\mu_{L}: \mathcal{K}(\mathcal{K}(L))\longrightarrow \mathcal{K}(L)$
are defined by
and
respectively.
Remark 4.3. When the category K is specifically taken as SOB or WF, the inducing order-SOB-ification monad or order-WF-ification monad is denoted by
![]() $\mathcal S$
or
$\mathcal S$
or
![]() $\mathcal W$
, where
$\mathcal W$
, where
![]() $\mathcal S$
is actually the order-sobrification monad constructed by Ho et al. to solve the Ho-Zhao problem in Ho et al. (2018).
$\mathcal S$
is actually the order-sobrification monad constructed by Ho et al. to solve the Ho-Zhao problem in Ho et al. (2018).
5. The Eilenberg-Moore Algebras of
 $\mathcal K$
$\mathcal K$
Recall that a
![]() $\mathcal{T}$
$\mathcal{T}$
![]() ${-algebra}$
(Mac Lane Reference Mac Lane1998) of a monad
${-algebra}$
(Mac Lane Reference Mac Lane1998) of a monad
![]() $(\mathcal{T}, \eta, \mu)$
is a pair
$(\mathcal{T}, \eta, \mu)$
is a pair
![]() $(C, \xi)$
, where C is an object of C and
$(C, \xi)$
, where C is an object of C and
![]() $\xi: \mathcal{T}C\rightarrow C$
is a morphism in C, that satisfies
$\xi: \mathcal{T}C\rightarrow C$
is a morphism in C, that satisfies
![]() $\xi\circ\mu_{C} = \xi\circ \mathcal{T}\xi$
and
$\xi\circ\mu_{C} = \xi\circ \mathcal{T}\xi$
and
![]() $\xi\circ \eta_{C} = id_{C}$
. In this case,
$\xi\circ \eta_{C} = id_{C}$
. In this case,
![]() $\xi$
is called a structure map. If both
$\xi$
is called a structure map. If both
![]() $(A, \xi_{A})$
and
$(A, \xi_{A})$
and
![]() $(B, \xi_{B})$
are
$(B, \xi_{B})$
are
![]() $\mathcal{T}$
-algebras, a
$\mathcal{T}$
-algebras, a
![]() $\mathcal T$
-algebra homomorphism from
$\mathcal T$
-algebra homomorphism from
![]() $(A, \xi_{A})$
to
$(A, \xi_{A})$
to
![]() $(B, \xi_{B})$
is an arrow
$(B, \xi_{B})$
is an arrow
![]() $h: A\rightarrow B$
satisfying
$h: A\rightarrow B$
satisfying
![]() $ h\circ \xi_{A} = \xi_{B}\circ \mathcal{T}h$
.
$ h\circ \xi_{A} = \xi_{B}\circ \mathcal{T}h$
.
For a monad
![]() $(\mathcal T, \eta, \mu)$
on the category C, the category of
$(\mathcal T, \eta, \mu)$
on the category C, the category of
![]() $\mathcal T$
-algebras determines with respect to what algebraic structures the functor
$\mathcal T$
-algebras determines with respect to what algebraic structures the functor
![]() $\mathcal T$
can be understood to be universal. More precisely, for each morphism f in
$\mathcal T$
can be understood to be universal. More precisely, for each morphism f in
![]() $\mathbf C$
which maps A to a
$\mathbf C$
which maps A to a
![]() $\mathcal T$
-algebra
$\mathcal T$
-algebra
![]() $(C, \xi)$
, there exists a unique
$(C, \xi)$
, there exists a unique
![]() $\mathcal T$
-algebra homomorphism
$\mathcal T$
-algebra homomorphism
![]() $h: \mathcal TA\rightarrow C$
such that
$h: \mathcal TA\rightarrow C$
such that
![]() $f = h\circ \eta_A$
. Identifying such structures is not only an interesting mathematical problem, but also could be useful for semantics. One can refer to Jia et al. (Reference Jia, Kornell, Lindenhovius, Mislove and Zamdzhiev2022) for example, where the authors proved that the category of algebras of the subprobability valuation monad on the category of domains is isomorphic to the category of so-called continuous Kegelspitzen, and this result plays a crucial role in giving an adequate semantics to variational quantum programming languages.
$f = h\circ \eta_A$
. Identifying such structures is not only an interesting mathematical problem, but also could be useful for semantics. One can refer to Jia et al. (Reference Jia, Kornell, Lindenhovius, Mislove and Zamdzhiev2022) for example, where the authors proved that the category of algebras of the subprobability valuation monad on the category of domains is isomorphic to the category of so-called continuous Kegelspitzen, and this result plays a crucial role in giving an adequate semantics to variational quantum programming languages.
Let
![]() $\mathbf{C}^{\mathcal{T}}$
denote the category of all
$\mathbf{C}^{\mathcal{T}}$
denote the category of all
![]() $\mathcal{T}$
-algebras and their homomorphisms, which is also called the Eilenberg-Moore category of
$\mathcal{T}$
-algebras and their homomorphisms, which is also called the Eilenberg-Moore category of
![]() $\mathcal{T}$
over
$\mathcal{T}$
over
![]() $\mathbf C$
. We proceed to characterize the
$\mathbf C$
. We proceed to characterize the
![]() $\mathcal K$
-algebras over
$\mathcal K$
-algebras over
![]() $\mathbf{DCPO}$
.
$\mathbf{DCPO}$
.
Definition 5.1. (1) A poset P is called k-complete if for every Scott closed
![]() ${\mathbf{K}^{*}}$
-set A of P,
${\mathbf{K}^{*}}$
-set A of P,
![]() $\sup A$
exists.
$\sup A$
exists.
(2) Let L and M be posets. A map
![]() $f: L\rightarrow M$
is called k-continuous if for any
$f: L\rightarrow M$
is called k-continuous if for any
![]() $A\in \mathcal{K}(L)$
whose supremum exists,
$A\in \mathcal{K}(L)$
whose supremum exists,
![]() $f(\sup A) = \sup f(A)$
.
$f(\sup A) = \sup f(A)$
.
When
![]() $\mathbf K^*$
is
$\mathbf K^*$
is
![]() $\mathbf {SOB}$
, k-complete posets are precisely strongly complete (Ho et al. Reference Ho, Goubault-Larrecq, Jung and Xi2018, Definition 2.1); when
$\mathbf {SOB}$
, k-complete posets are precisely strongly complete (Ho et al. Reference Ho, Goubault-Larrecq, Jung and Xi2018, Definition 2.1); when
![]() $\mathbf K^*$
is
$\mathbf K^*$
is
![]() $\mathbf {WF}$
, we call a k-complete poset P w-complete, that is, every Scott closed well-filtered determined subset of P has a supremum in P.
$\mathbf {WF}$
, we call a k-complete poset P w-complete, that is, every Scott closed well-filtered determined subset of P has a supremum in P.
Since directed subsets are tapered, they are
![]() $\mathbf{K}^{*}$
-sets by Lemma 3.10. Then the following results are immediately obtained.
$\mathbf{K}^{*}$
-sets by Lemma 3.10. Then the following results are immediately obtained.
Proposition 5.2.
-
(1) Every k-complete poset is a dcpo.
-
(2) Each k-continuous map between two posets is Scott-continuous.
Readers will be referred to Escardó (Reference Escardó1998) for the notions mentioned in the following.
A category C is called poset-enriched if the set of its hom-sets is a poset and its composition operation is monotone. A poset-functor between poset-enriched categories is a functor which is monotone on hom-posets. One can easily see that
![]() $\mathbf{DCPO}$
is a poset-enriched category and
$\mathbf{DCPO}$
is a poset-enriched category and
![]() $\mathcal{K}$
is a poset-functor. If there is a pair of arrows
$\mathcal{K}$
is a poset-functor. If there is a pair of arrows
![]() $l: X\rightarrow Y$
and
$l: X\rightarrow Y$
and
![]() $r: Y\rightarrow X$
in C such that
$r: Y\rightarrow X$
in C such that
![]() $l\circ r\leq {\mathrm{id}}_{Y}$
and
$l\circ r\leq {\mathrm{id}}_{Y}$
and
![]() $r\circ l\geq {\mathrm{id}}_{X}$
, then l is said to be a left adjoint of r, denoted by
$r\circ l\geq {\mathrm{id}}_{X}$
, then l is said to be a left adjoint of r, denoted by
![]() $l\dashv r$
. The adjunction
$l\dashv r$
. The adjunction
![]() $l\dashv r$
is reflective if
$l\dashv r$
is reflective if
![]() $l\circ r = {\mathrm{id}}_{Y}$
. A monad
$l\circ r = {\mathrm{id}}_{Y}$
. A monad
![]() $\mathcal{T} = (\mathcal{T}, \eta, \mu)$
on a poset-enriched category
$\mathcal{T} = (\mathcal{T}, \eta, \mu)$
on a poset-enriched category
![]() $\mathcal{C}$
is called a left KZ-monad if and only if
$\mathcal{C}$
is called a left KZ-monad if and only if
![]() $\mathcal{T}$
is a poset-functor and
$\mathcal{T}$
is a poset-functor and
![]() $ \mu_{C}\dashv\eta_{\mathcal{T}C}$
for all
$ \mu_{C}\dashv\eta_{\mathcal{T}C}$
for all
![]() $C\in \mathcal{C}$
. In addition, if
$C\in \mathcal{C}$
. In addition, if
![]() $\mathcal{F}: \mathbf{C}\rightarrow \mathbf{C}$
is a poset-functor, we shall say that a map
$\mathcal{F}: \mathbf{C}\rightarrow \mathbf{C}$
is a poset-functor, we shall say that a map
![]() $f: X\rightarrow Y$
in
$f: X\rightarrow Y$
in
![]() $\mathbf{C}$
is a left
$\mathbf{C}$
is a left
![]() $\mathcal{F}$
-embedding if
$\mathcal{F}$
-embedding if
![]() $\mathcal{F}f$
has a right adjoint and the adjunction is reflective.
$\mathcal{F}f$
has a right adjoint and the adjunction is reflective.
Proposition 5.3.
![]() $\mathcal{K}$
is a left KZ-monad over the poset-enriched category
$\mathcal{K}$
is a left KZ-monad over the poset-enriched category
![]() $\mathbf{DCPO}$
.
$\mathbf{DCPO}$
.
Proof. We just need to prove that
![]() $\mu_{L}\dashv \eta_{\mathcal{K}(L)}$
for any dcpo L. On the one hand, it follows immediately from the monad law that
$\mu_{L}\dashv \eta_{\mathcal{K}(L)}$
for any dcpo L. On the one hand, it follows immediately from the monad law that
![]() $\mu_{L}\circ\eta_{\mathcal{K}(L)} = {\mathrm{id}}_{\mathcal{K}(L)}$
holds. On the other hand, for any
$\mu_{L}\circ\eta_{\mathcal{K}(L)} = {\mathrm{id}}_{\mathcal{K}(L)}$
holds. On the other hand, for any
![]() $\mathcal{A}\in \mathcal{K}(\mathcal{K}(L))$
,
$\mathcal{A}\in \mathcal{K}(\mathcal{K}(L))$
,
which means
![]() $\eta_{\mathcal{K}(L)}\circ\mu_{L}\geq {\mathrm{id}}_{\mathcal{K}(\mathcal{K}(L))}$
. So
$\eta_{\mathcal{K}(L)}\circ\mu_{L}\geq {\mathrm{id}}_{\mathcal{K}(\mathcal{K}(L))}$
. So
![]() $\mu_{L}\dashv \eta_{\mathcal{K}(L)}$
; hence,
$\mu_{L}\dashv \eta_{\mathcal{K}(L)}$
; hence,
![]() $\mathcal{K}$
is a left KZ-monad over
$\mathcal{K}$
is a left KZ-monad over
![]() $\mathbf{DCPO}$
.
$\mathbf{DCPO}$
.
We fully characterize the Eilenberg-Moore algebras of the monad
![]() $\mathcal K$
in the following theorem.
$\mathcal K$
in the following theorem.
Theorem 5.4. Let L be a dcpo. The following statements are equivalent.
-
(1) There exists a structure map
 $\alpha: \mathcal{K}(L)\rightarrow L$
such that
$\alpha: \mathcal{K}(L)\rightarrow L$
such that
 $(L, \alpha)$
is a
$(L, \alpha)$
is a
 $\mathcal{K}$
-algebra.
$\mathcal{K}$
-algebra. -
(2) L is an injective object over left
 $\mathcal{K}$
-embeddings.
$\mathcal{K}$
-embeddings.
-
(3) L is a k-complete poset.
Proof.
![]() $(1)\Rightarrow (2)$
: It is immediate by Escardó (Reference Escardó1998, Theorem 4.2.2).
$(1)\Rightarrow (2)$
: It is immediate by Escardó (Reference Escardó1998, Theorem 4.2.2).
![]() $(2)\Rightarrow (3)$
: One can derive from the monad law that
$(2)\Rightarrow (3)$
: One can derive from the monad law that
![]() $\mu_L\circ \mathcal K\eta_L = id_{\mathcal K(L)}$
, which reveals that
$\mu_L\circ \mathcal K\eta_L = id_{\mathcal K(L)}$
, which reveals that
![]() $\eta_L$
is a left embedding. So there is an extension
$\eta_L$
is a left embedding. So there is an extension
![]() $m: \mathcal K(L)\rightarrow L$
of the identity of L along
$m: \mathcal K(L)\rightarrow L$
of the identity of L along
![]() $\eta_L$
by (2). This entails that
$\eta_L$
by (2). This entails that
![]() $m\circ \eta_L = id_L$
. Let A be a Scott closed
$m\circ \eta_L = id_L$
. Let A be a Scott closed
![]() $\mathbf K^{*}$
-set of L. We claim that
$\mathbf K^{*}$
-set of L. We claim that
![]() $\sup A = m(A)$
exists. For each
$\sup A = m(A)$
exists. For each
![]() $a\in A$
,
$a\in A$
,
![]() $\downarrow\!\!a\subseteq A$
. Since m is monotone,
$\downarrow\!\!a\subseteq A$
. Since m is monotone,
![]() $m(\downarrow\!\!a)\leq m(A)$
, which means
$m(\downarrow\!\!a)\leq m(A)$
, which means
![]() $a = m\circ\eta(a)\leq m(A)$
. If b is another upper bound of A, then
$a = m\circ\eta(a)\leq m(A)$
. If b is another upper bound of A, then
![]() $A\subseteq \downarrow\!b$
. By the monotonicity of m again, we have
$A\subseteq \downarrow\!b$
. By the monotonicity of m again, we have
![]() $m(A)\leq m(\downarrow\!b) = b$
. Thus,
$m(A)\leq m(\downarrow\!b) = b$
. Thus,
![]() $\sup A = m(A)$
exists and L is a k-complete poset.
$\sup A = m(A)$
exists and L is a k-complete poset.
![]() $(3)\Rightarrow (1)$
: Since
$(3)\Rightarrow (1)$
: Since
![]() $\sup A$
exists for each
$\sup A$
exists for each
![]() $A\in \mathcal{K}(L)$
, we could define a map
$A\in \mathcal{K}(L)$
, we could define a map
![]() $\alpha: \mathcal{K}(L)\rightarrow L$
by
$\alpha: \mathcal{K}(L)\rightarrow L$
by
Then, one can easily verify that
![]() $\alpha$
is Scott-continuous, besides,
$\alpha$
is Scott-continuous, besides,
![]() $\alpha\circ\eta = {\mathrm{id}}_{L}$
and
$\alpha\circ\eta = {\mathrm{id}}_{L}$
and
![]() $\alpha\circ\mu = \alpha\circ\mathcal{K}\alpha$
hold. So
$\alpha\circ\mu = \alpha\circ\mathcal{K}\alpha$
hold. So
![]() $(L, \alpha)$
is a
$(L, \alpha)$
is a
![]() $\mathcal{K}$
-algebra.
$\mathcal{K}$
-algebra.
By definitions of the
![]() $\mathcal{K}$
-algebra homomorphisms and the k-continuity, the following conclusion is obtained immediately, which will help us characterize the Eilenberg-Moore category of
$\mathcal{K}$
-algebra homomorphisms and the k-continuity, the following conclusion is obtained immediately, which will help us characterize the Eilenberg-Moore category of
![]() $\mathcal K$
.
$\mathcal K$
.
Proposition 5.5. Let L, M be dcpos. If
![]() $(L, \alpha_{L})$
and
$(L, \alpha_{L})$
and
![]() $(M, \alpha_{M})$
are
$(M, \alpha_{M})$
are
![]() $\mathcal{K}$
-algebras, then
$\mathcal{K}$
-algebras, then
![]() $f: L\rightarrow M$
is a
$f: L\rightarrow M$
is a
![]() $\mathcal{K}$
-algebra homomorphism if and only if f is k-continuous.
$\mathcal{K}$
-algebra homomorphism if and only if f is k-continuous.
Now let
![]() $\mathbf{DCPO}^{\mathcal{K}}$
denote the category of all
$\mathbf{DCPO}^{\mathcal{K}}$
denote the category of all
![]() $\mathcal K$
-algebras and all
$\mathcal K$
-algebras and all
![]() $\mathcal K$
-algebra homomorphisms, that is the Eilenberg-Moore category of
$\mathcal K$
-algebra homomorphisms, that is the Eilenberg-Moore category of
![]() $\mathcal K$
. Then obviously,
$\mathcal K$
. Then obviously,
![]() $\mathcal{K}$
produces a monadic adjunction:
$\mathcal{K}$
produces a monadic adjunction:
where
![]() $\mathcal{F}$
assigns each dcpo L to
$\mathcal{F}$
assigns each dcpo L to
![]() $(\mathcal{K}(L), \mu_{L})$
and each map
$(\mathcal{K}(L), \mu_{L})$
and each map
![]() $f: L\rightarrow M$
from L to dcpo M to
$f: L\rightarrow M$
from L to dcpo M to
![]() $\mathcal{K}(f): (\mathcal{K}(L), \mu_{L})\rightarrow(\mathcal{K}(M), \mu_{M})$
, and
$\mathcal{K}(f): (\mathcal{K}(L), \mu_{L})\rightarrow(\mathcal{K}(M), \mu_{M})$
, and
![]() $\mathcal U$
as a forgetful functor is the right adjoint of
$\mathcal U$
as a forgetful functor is the right adjoint of
![]() $\mathcal F$
. As the characterizations of
$\mathcal F$
. As the characterizations of
![]() $\mathcal{K}$
-algebras and their homomorphisms imply that
$\mathcal{K}$
-algebras and their homomorphisms imply that
![]() $\mathbf{DCPO}^{\mathcal{K}}$
is equivalent to the category
$\mathbf{DCPO}^{\mathcal{K}}$
is equivalent to the category
![]() $\mathbf{KCPO}$
, which has the k-complete posets as objects and the k-continuous maps as morphisms, we reach the following conclusion:
$\mathbf{KCPO}$
, which has the k-complete posets as objects and the k-continuous maps as morphisms, we reach the following conclusion:
Corollary 5.6.
![]() $\mathcal{K}$
gives a free k-complete poset construction over
$\mathcal{K}$
gives a free k-complete poset construction over
![]() $\mathbf{DCPO}$
.
$\mathbf{DCPO}$
.
In Zhao and Fan (Reference Zhao and Fan2010), Zhao and Fan have proved that the category
![]() $\mathbf{DCPO}$
is a reflective full subcategory of the category
$\mathbf{DCPO}$
is a reflective full subcategory of the category
![]() $\mathbf{POS}_{\mathbf{d}}$
of posets and Scott-continuous maps. Thus combining the above corollary, the following result can be derived immediately:
$\mathbf{POS}_{\mathbf{d}}$
of posets and Scott-continuous maps. Thus combining the above corollary, the following result can be derived immediately:
Corollary 5.7.
![]() $\mathcal{K}$
gives a free k-complete poset construction over
$\mathcal{K}$
gives a free k-complete poset construction over
![]() $\mathbf{POS}_{\mathbf{d}}$
.
$\mathbf{POS}_{\mathbf{d}}$
.
Let
![]() $\mathbf{KCPO}_{\sigma}$
be the full subcategory of
$\mathbf{KCPO}_{\sigma}$
be the full subcategory of
![]() $\mathbf{DCPO}$
which has k-complete posets as objects and Scott-continuous maps as morphisms.
$\mathbf{DCPO}$
which has k-complete posets as objects and Scott-continuous maps as morphisms.
It is a truism that Cartesian closed categories give rise to the models of various typed and untyped
![]() $\lambda$
-calculi and functional programming languages (Lambek Reference Lambek1985; Scott Reference Scott1976; Streicher Reference Streicher2006). We will see in the following theorem that similar to the category DCPO,
$\lambda$
-calculi and functional programming languages (Lambek Reference Lambek1985; Scott Reference Scott1976; Streicher Reference Streicher2006). We will see in the following theorem that similar to the category DCPO,
![]() $\mathbf{KCPO}_{\sigma}$
is Cartesian closed for each category
$\mathbf{KCPO}_{\sigma}$
is Cartesian closed for each category
![]() $\mathbf K^*$
of type
$\mathbf K^*$
of type
![]() $\mathrm K^*$
.
$\mathrm K^*$
.
Proposition 5.8. The category
![]() $\mathbf{KCPO}_{\sigma}$
is Cartesian closed.
$\mathbf{KCPO}_{\sigma}$
is Cartesian closed.
Proof. Since
![]() $\mathbf{KCPO}_{\sigma}$
is a full subcategory of
$\mathbf{KCPO}_{\sigma}$
is a full subcategory of
![]() $\mathbf{DCPO}$
, we only need to prove that for any k-complete posets L and M,
$\mathbf{DCPO}$
, we only need to prove that for any k-complete posets L and M,
![]() $L\times M$
and
$L\times M$
and
![]() $[L\rightarrow M]$
(the set of all Scott-continuous maps between L and M) are still k-complete posets.
$[L\rightarrow M]$
(the set of all Scott-continuous maps between L and M) are still k-complete posets.
![]() $\mathbf{Claim\ 1}$
:
$\mathbf{Claim\ 1}$
:
![]() $L\times M$
is a k-complete poset.
$L\times M$
is a k-complete poset.
Let
![]() $A\subseteq L\times M$
be a Scott closed
$A\subseteq L\times M$
be a Scott closed
![]() $\mathbf{K}^{\mathbf{*}}$
-set. Then, A is a
$\mathbf{K}^{\mathbf{*}}$
-set. Then, A is a
![]() $\mathbf{K}^{\mathbf{*}}$
-set in
$\mathbf{K}^{\mathbf{*}}$
-set in
![]() $\Sigma L\times \Sigma M$
. Since the projections
$\Sigma L\times \Sigma M$
. Since the projections
![]() $\pi_{L}$
and
$\pi_{L}$
and
![]() $\pi_{M}$
are continuous,
$\pi_{M}$
are continuous,
![]() $\pi_{L}(A)$
and
$\pi_{L}(A)$
and
![]() $\pi_{M}(A)$
are
$\pi_{M}(A)$
are
![]() $\mathbf{K}^{\mathbf{*}}$
-sets of L and M, respectively. The fact that L and M are k-complete posets implies the existence of
$\mathbf{K}^{\mathbf{*}}$
-sets of L and M, respectively. The fact that L and M are k-complete posets implies the existence of
![]() $\sup(\pi_{L}(A))$
and
$\sup(\pi_{L}(A))$
and
![]() $\sup(\pi_{M}(A))$
. One can verify that
$\sup(\pi_{M}(A))$
. One can verify that
![]() $(\sup(\pi_{L}(A)), \sup(\pi_{M}(A)))$
is the supremum of A. So
$(\sup(\pi_{L}(A)), \sup(\pi_{M}(A)))$
is the supremum of A. So
![]() $L\times M$
is a k-complete poset.
$L\times M$
is a k-complete poset.
![]() $\mathbf{Claim\ 2}$
:
$\mathbf{Claim\ 2}$
:
![]() $[L\rightarrow M]$
is a k-complete poset.
$[L\rightarrow M]$
is a k-complete poset.
Let
![]() $\{f_{i}: i\in I\}\subseteq [L\rightarrow M]$
be a
$\{f_{i}: i\in I\}\subseteq [L\rightarrow M]$
be a
![]() $\mathbf{K}^{\mathbf{*}}$
-set. We define
$\mathbf{K}^{\mathbf{*}}$
-set. We define
![]() $g: L\rightarrow M$
by
$g: L\rightarrow M$
by
By Lemma 2-2.8 and Lemma 2-2.9 in Gierz et al. (Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003), we know the map
![]() $eval_{x}: [L\rightarrow M]\rightarrow M$
defined by
$eval_{x}: [L\rightarrow M]\rightarrow M$
defined by
![]() $eval_{x}(h) = h(x)$
is continuous. Thus,
$eval_{x}(h) = h(x)$
is continuous. Thus,
![]() $eval_{x}(\{f_{i}: i\in I\}) = \{f_{i}(x): i\in I\}$
is a
$eval_{x}(\{f_{i}: i\in I\}) = \{f_{i}(x): i\in I\}$
is a
![]() $\mathbf{K}^{\mathbf{*}}$
-set of M. Since M is k-complete,
$\mathbf{K}^{\mathbf{*}}$
-set of M. Since M is k-complete,
![]() $\sup\{f_{i}(x): i\in I\}$
exists in M. This means g is well-defined. Obviously, g is Scott-continuous and
$\sup\{f_{i}(x): i\in I\}$
exists in M. This means g is well-defined. Obviously, g is Scott-continuous and
![]() $g = \sup\{f_{i}: i\in I\}$
. Thus,
$g = \sup\{f_{i}: i\in I\}$
. Thus,
![]() $[L\rightarrow M]$
is k-complete.
$[L\rightarrow M]$
is k-complete.
In conclusion,
![]() $\mathbf{KCPO}_{\sigma}$
is Cartesian closed.
$\mathbf{KCPO}_{\sigma}$
is Cartesian closed.
6.
 $\mathcal K$
is a Commutative Monad
$\mathcal K$
is a Commutative Monad
Recall that a monoidal category (see Borceux Reference Borceux1994, Definition 6.1.1) is a category C equipped with an object
![]() $\top$
in
$\top$
in
![]() $\mathbf C$
called unit, a bifunctor
$\mathbf C$
called unit, a bifunctor
![]() $\otimes: \mathbf C\times \mathbf C\rightarrow \mathbf C$
called tensor product, and the natural isomorphisms
$\otimes: \mathbf C\times \mathbf C\rightarrow \mathbf C$
called tensor product, and the natural isomorphisms
![]() $\alpha, r$
and l defined as the following forms (for the objects A, B and C):
$\alpha, r$
and l defined as the following forms (for the objects A, B and C):
-
(i)
 $ {\alpha_{A, B, C}}: A \otimes (B \otimes C) \rightarrow (A \otimes B) \otimes C$
,
$ {\alpha_{A, B, C}}: A \otimes (B \otimes C) \rightarrow (A \otimes B) \otimes C$
, -
(ii)
 $r_A: A\otimes \top \rightarrow A$
,
$r_A: A\otimes \top \rightarrow A$
, -
(iii)
 $l_A: \top\otimes A \rightarrow A$
, such that certain equations hold. It will be a symmetric monoidal category if in addition it has the natural isomorphism s defined as the form:
$l_A: \top\otimes A \rightarrow A$
, such that certain equations hold. It will be a symmetric monoidal category if in addition it has the natural isomorphism s defined as the form: -
(iv)
 $ {s_{A, B}}: A\otimes B\rightarrow B\otimes A$
,
$ {s_{A, B}}: A\otimes B\rightarrow B\otimes A$
,
such that certain equations hold. It was Kock who first defined strong monads over symmetric monoidal categories (Kock Reference Kock1972). In this section we will first investigate the strongness of the monad
![]() $\mathcal K$
induced by the category
$\mathcal K$
induced by the category
![]() $\mathbf K^*$
of type
$\mathbf K^*$
of type
![]() $\mathrm K^*$
on
$\mathrm K^*$
on
![]() $\mathbf{DCPO}$
, where
$\mathbf{DCPO}$
, where
![]() $\mathbf{DCPO}$
is clearly a Cartesian monoidal category. In this case, the tensor product
$\mathbf{DCPO}$
is clearly a Cartesian monoidal category. In this case, the tensor product
![]() $\otimes$
is precisely the categorical product and
$\otimes$
is precisely the categorical product and
![]() $\top$
is the terminal object, we use
$\top$
is the terminal object, we use
![]() $\times$
and 1 to represent them respectively. Moreover,
$\times$
and 1 to represent them respectively. Moreover,
![]() $\alpha(A, B, C), r_A, l_A$
are defined concretely as follows:
$\alpha(A, B, C), r_A, l_A$
are defined concretely as follows:
-
(i)
 $\alpha_{A, B, C} = ((\pi_1, \pi_1\circ\pi_2), \pi_2\circ\pi_2))$
,
$\alpha_{A, B, C} = ((\pi_1, \pi_1\circ\pi_2), \pi_2\circ\pi_2))$
, -
(ii)
 $r_A = \pi_1$
,
$r_A = \pi_1$
, -
(iii)
 $l_A = \pi_2$
,
$l_A = \pi_2$
,
where
![]() $\pi_{i}(i = 1,2)$
denotes the projection onto the
$\pi_{i}(i = 1,2)$
denotes the projection onto the
![]() $i{\rm th}$
component.
$i{\rm th}$
component.
Definition 6.1. A strong monad over a category
![]() $\mathbf{C}$
with an object 1 and finite products is a monad
$\mathbf{C}$
with an object 1 and finite products is a monad
![]() $(\mathcal T,\eta,\mu)$
together with a natural transformation
$(\mathcal T,\eta,\mu)$
together with a natural transformation
![]() $t'': ({-})\times \mathcal T({=})\rightarrow \mathcal T({-}\times{=})$
such that the following diagrams commute:
$t'': ({-})\times \mathcal T({=})\rightarrow \mathcal T({-}\times{=})$
such that the following diagrams commute:
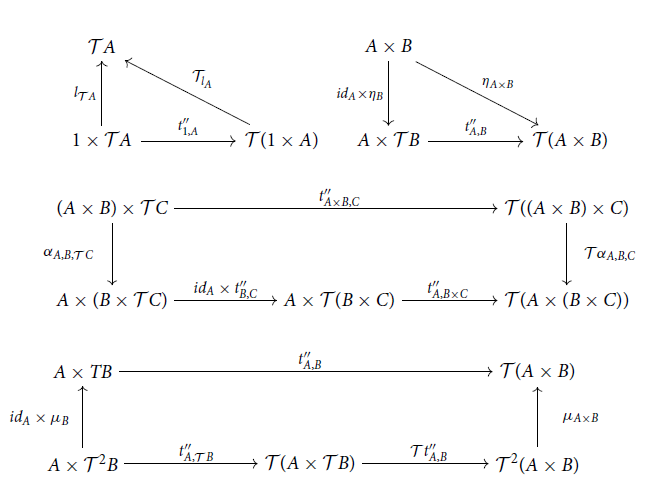
in which the natural transformation t” is called tensorial strength. Moreover,
![]() $t' = \mathcal Ts\circ t''\circ s: \mathcal T({-})\times (=)\rightarrow \mathcal T({-}\times =)$
is called cotensorial strength.
$t' = \mathcal Ts\circ t''\circ s: \mathcal T({-})\times (=)\rightarrow \mathcal T({-}\times =)$
is called cotensorial strength.
Lemma 6.2. Let P and Q be posets. Then,
![]() $cl_{\sigma}(A)\times B = cl_{\sigma}(A\times B)$
for any
$cl_{\sigma}(A)\times B = cl_{\sigma}(A\times B)$
for any
![]() $A\subseteq P$
and
$A\subseteq P$
and
![]() $B\in \Gamma(Q)$
.
$B\in \Gamma(Q)$
.
Proof. It is obvious that
![]() $cl_{\sigma}(A\times B)\subseteq cl_{\sigma}(A)\times B$
since
$cl_{\sigma}(A\times B)\subseteq cl_{\sigma}(A)\times B$
since
![]() $cl_{\sigma}(A)\times B$
is closed in
$cl_{\sigma}(A)\times B$
is closed in
![]() $\Sigma(P\times Q)$
. Now see the reverse. For any
$\Sigma(P\times Q)$
. Now see the reverse. For any
![]() $(a,b)\in cl_{\sigma}(A)\times B$
and
$(a,b)\in cl_{\sigma}(A)\times B$
and
![]() $U\in \sigma(P\times Q)$
with
$U\in \sigma(P\times Q)$
with
![]() $(a, b)\in U$
. Set
$(a, b)\in U$
. Set
![]() $U_{b} = \{x\in P: (x, b)\in U\}$
. Clearly,
$U_{b} = \{x\in P: (x, b)\in U\}$
. Clearly,
![]() $a\in U_b$
and it is an upper set. Let
$a\in U_b$
and it is an upper set. Let
![]() $D\subseteq P$
be a directed subset with
$D\subseteq P$
be a directed subset with
![]() $\sup D\in U_{b}$
, that is,
$\sup D\in U_{b}$
, that is,
![]() $(\sup D, b)\in U$
. Then, we have
$(\sup D, b)\in U$
. Then, we have
![]() $(d_{0}, b)\in U$
for some
$(d_{0}, b)\in U$
for some
![]() $d_{0}\in D$
by the Scott openness of U, which implies that
$d_{0}\in D$
by the Scott openness of U, which implies that
![]() $d_{0}\in U_{b}$
. Thus,
$d_{0}\in U_{b}$
. Thus,
![]() $U_{b}\in \sigma(P)$
. Then,
$U_{b}\in \sigma(P)$
. Then,
![]() $A\cap U_{b} \neq\emptyset$
by
$A\cap U_{b} \neq\emptyset$
by
![]() $a\in cl_{\sigma}(A)$
, so there is an
$a\in cl_{\sigma}(A)$
, so there is an
![]() $a_{0}\in A\cap U_{b}$
. It follows that
$a_{0}\in A\cap U_{b}$
. It follows that
![]() $(a_{0}, b)\in (A\times B)\cap U$
. Therefore,
$(a_{0}, b)\in (A\times B)\cap U$
. Therefore,
![]() $(a, b)\in cl_{\sigma}(A\times B)$
and
$(a, b)\in cl_{\sigma}(A\times B)$
and
![]() $cl_{\sigma}(A)\times B\subseteq cl_{\sigma}(A\times B)$
.
$cl_{\sigma}(A)\times B\subseteq cl_{\sigma}(A\times B)$
.
Proposition 6.3.
![]() $\mathcal{K}$
is a strong monad over
$\mathcal{K}$
is a strong monad over
![]() $\mathbf{DCPO}$
.
$\mathbf{DCPO}$
.
Proof. Obviously, the direct product
![]() $L_{1}\times\cdot\cdot\cdot\times L_{n}$
of finitely many dcpos
$L_{1}\times\cdot\cdot\cdot\times L_{n}$
of finitely many dcpos
![]() $L_{1},...,L_{n}$
is still a dcpo. Given
$L_{1},...,L_{n}$
is still a dcpo. Given
![]() $\{L,M,N\}\subseteq \mathbf{DCPO}$
, we define
$\{L,M,N\}\subseteq \mathbf{DCPO}$
, we define
![]() $l_{L}$
as
$l_{L}$
as
![]() $\pi_{2}$
and
$\pi_{2}$
and
![]() $\alpha_{L,M,N}: (L\times M)\times N\rightarrow L\times (M\times N)$
as
$\alpha_{L,M,N}: (L\times M)\times N\rightarrow L\times (M\times N)$
as
![]() $(\pi_{1}\circ\pi_{1},(\pi_{2}\circ\pi_{1},\pi_{2}))$
. Define
$(\pi_{1}\circ\pi_{1},(\pi_{2}\circ\pi_{1},\pi_{2}))$
. Define
![]() $t''_{L,M}:L\times \mathcal{K}(M)\longrightarrow \mathcal{K}(L\times M)$
by
$t''_{L,M}:L\times \mathcal{K}(M)\longrightarrow \mathcal{K}(L\times M)$
by
![]() $\mathbf{Claim\; 1}$
:
$\mathbf{Claim\; 1}$
:
![]() $t''_{L,M}$
is well-defined.
$t''_{L,M}$
is well-defined.
It is sufficient to show that
![]() $\downarrow$
$\downarrow$
![]() $x\times A\in \mathcal{K}(L\times M)$
. Obviously,
$x\times A\in \mathcal{K}(L\times M)$
. Obviously,
![]() $\downarrow$
$\downarrow$
![]() $x\times A$
is closed in
$x\times A$
is closed in
![]() $\Sigma(L\times M)$
. Now we prove that
$\Sigma(L\times M)$
. Now we prove that
![]() $\downarrow$
$\downarrow$
![]() $x\times A$
is a
$x\times A$
is a
![]() $\mathbf{K}^{*}$
-set in
$\mathbf{K}^{*}$
-set in
![]() $\Sigma(L\times M)$
. For any
$\Sigma(L\times M)$
. For any
![]() $\mathbf{K}^{*}$
-space Y and the continuous map
$\mathbf{K}^{*}$
-space Y and the continuous map
![]() $f: L\times M\rightarrow Y$
, we fix
$f: L\times M\rightarrow Y$
, we fix
![]() $x\in L$
and define
$x\in L$
and define
![]() $f_{x}: M\rightarrow Y$
as
$f_{x}: M\rightarrow Y$
as
which is well-defined. Now claim that
![]() $f_{x}$
is continuous, i.e.,
$f_{x}$
is continuous, i.e.,
![]() $f_{x}^{-1}(U)\in \sigma(M)$
for each
$f_{x}^{-1}(U)\in \sigma(M)$
for each
![]() $U\in \mathcal{O}(Y)$
. For any
$U\in \mathcal{O}(Y)$
. For any
![]() $a_{1}\in f_{x}^{-1}(U)$
and
$a_{1}\in f_{x}^{-1}(U)$
and
![]() $a_{2}\in M$
with
$a_{2}\in M$
with
![]() $a_{1}\leq a_{2}$
,
$a_{1}\leq a_{2}$
,
![]() $f_{x}(a_{1}) = f(x,a_{1})\in U$
, that is,
$f_{x}(a_{1}) = f(x,a_{1})\in U$
, that is,
![]() $(x,a_{1})\in f^{-1}(U)\in \sigma(L\times M)$
. The fact
$(x,a_{1})\in f^{-1}(U)\in \sigma(L\times M)$
. The fact
![]() $(x,a_{2})\geq (x,a_{1})$
implies
$(x,a_{2})\geq (x,a_{1})$
implies
![]() $(x,a_{2})\in f^{-1}(U)$
, and so
$(x,a_{2})\in f^{-1}(U)$
, and so
![]() $f_{x}(a_{2})\in U$
. Thus
$f_{x}(a_{2})\in U$
. Thus
![]() $f_{x}^{-1}(U)$
is an upper set. Now let
$f_{x}^{-1}(U)$
is an upper set. Now let
![]() $D\subseteq M$
be a directed subset with
$D\subseteq M$
be a directed subset with
![]() $\sup D\in f_{x}^{-1}(U)$
. Then,
$\sup D\in f_{x}^{-1}(U)$
. Then,
![]() $(x, \sup D)\in f^{-1}(U)$
. It follows that there exists a
$(x, \sup D)\in f^{-1}(U)$
. It follows that there exists a
![]() $d\in D$
such that
$d\in D$
such that
![]() $(x,d)\in f^{-1}(U)$
, that is,
$(x,d)\in f^{-1}(U)$
, that is,
![]() $d\in f_{x}^{-1}(U)$
. Thus,
$d\in f_{x}^{-1}(U)$
. Thus,
![]() $f_{x}$
is continuous, which guarantees that
$f_{x}$
is continuous, which guarantees that
![]() $f_{x}(A)$
is a
$f_{x}(A)$
is a
![]() $\mathbf{K}^{*}$
-set of Y by Lemma 3.6. Since Y is a
$\mathbf{K}^{*}$
-set of Y by Lemma 3.6. Since Y is a
![]() $\mathbf{K}^{*}$
-space,
$\mathbf{K}^{*}$
-space,
![]() $\overline{f_{x}(A)} = \overline{\{f(x,a): a\in A\}} = \overline{\{y_{0}\}}$
for some
$\overline{f_{x}(A)} = \overline{\{f(x,a): a\in A\}} = \overline{\{y_{0}\}}$
for some
![]() $y_{0}\in Y$
. This means
$y_{0}\in Y$
. This means
![]() $\overline{f(\downarrow\!\!x\times A)} = \overline{\{y_{0}\},}$
and hence,
$\overline{f(\downarrow\!\!x\times A)} = \overline{\{y_{0}\},}$
and hence,
![]() $\downarrow$
$\downarrow$
![]() $x\times A$
is a
$x\times A$
is a
![]() $\mathbf{K}^{*}$
-set of
$\mathbf{K}^{*}$
-set of
![]() $L\times M$
.
$L\times M$
.
![]() $\mathbf{Claim\; 2}$
:
$\mathbf{Claim\; 2}$
:
![]() $t''_{L,M}$
is Scott-continuous.
$t''_{L,M}$
is Scott-continuous.
We just need to prove
![]() $t''_{L,M}$
is Scott-continuous in each component. Fixed
$t''_{L,M}$
is Scott-continuous in each component. Fixed
![]() $A\in \mathcal{K}(M)$
, for any directed subset
$A\in \mathcal{K}(M)$
, for any directed subset
![]() $D\subseteq L$
, we have
$D\subseteq L$
, we have
 \begin{align*} t''_{L,M}(\sup D, A) &= \downarrow\!\!\sup D\times A \\ &= \overline{\bigcup_{d\in D}\downarrow\!\!d}\times A \\ &= \overline{\bigcup_{d\in D}(\downarrow\!\!d\times A)} \\ &= \sup\{t''_{L,M}(d, A): d\in D\}, \end{align*}
\begin{align*} t''_{L,M}(\sup D, A) &= \downarrow\!\!\sup D\times A \\ &= \overline{\bigcup_{d\in D}\downarrow\!\!d}\times A \\ &= \overline{\bigcup_{d\in D}(\downarrow\!\!d\times A)} \\ &= \sup\{t''_{L,M}(d, A): d\in D\}, \end{align*}
where Lemma 6.2 guarantees the third equation. It follows that
![]() $t''_{L,M}$
is Scott-continuous in the first component. Next, given
$t''_{L,M}$
is Scott-continuous in the first component. Next, given
![]() $x\in L$
, let
$x\in L$
, let
![]() $\{A_{i}: i\in I\}$
be a directed family of
$\{A_{i}: i\in I\}$
be a directed family of
![]() $\mathcal{K}(M)$
. We have
$\mathcal{K}(M)$
. We have
 \begin{align*} t''_{L,M}(x, \sup_{i\in I}A_{i}) &= \downarrow\!\!x\times \sup_{i\in I}A_{i} \\ &= \downarrow\!\!x\times \overline{\bigcup_{i\in I}A_{i}} \\ &= \overline{\bigcup_{i\in I}(\downarrow\!\!x\times A_{i})} \\ &= \sup_{i\in I}t''_{L,M}(x, A_{i}). \end{align*}
\begin{align*} t''_{L,M}(x, \sup_{i\in I}A_{i}) &= \downarrow\!\!x\times \sup_{i\in I}A_{i} \\ &= \downarrow\!\!x\times \overline{\bigcup_{i\in I}A_{i}} \\ &= \overline{\bigcup_{i\in I}(\downarrow\!\!x\times A_{i})} \\ &= \sup_{i\in I}t''_{L,M}(x, A_{i}). \end{align*}
So
![]() $t''_{L,M}$
is Scott-continuous in the second component, and it is concluded that
$t''_{L,M}$
is Scott-continuous in the second component, and it is concluded that
![]() $t''_{L,M}$
is Scott-continuous.
$t''_{L,M}$
is Scott-continuous.
![]() $\mathbf{Claim\; 3}$
:
$\mathbf{Claim\; 3}$
:
![]() $t''_{L,M}$
is a natural transformation, that is, the following diagram commutes:
$t''_{L,M}$
is a natural transformation, that is, the following diagram commutes:

where L’, M’ are dcpos and
![]() $f: L\rightarrow L'$
,
$f: L\rightarrow L'$
,
![]() $g: M\rightarrow M'$
are Scott-continuous maps.
$g: M\rightarrow M'$
are Scott-continuous maps.
Now pick
![]() $(m, A)\in L\times \mathcal{K}(M)$
to prove that
$(m, A)\in L\times \mathcal{K}(M)$
to prove that
![]() $(\mathcal{K}(f\times g)\circ t''_{L,M})(m, A) = (t''_{L',M'}\circ f\times \mathcal{K}(g))(m, A)$
. By the facts that
$(\mathcal{K}(f\times g)\circ t''_{L,M})(m, A) = (t''_{L',M'}\circ f\times \mathcal{K}(g))(m, A)$
. By the facts that
 \begin{align*} (\mathcal{K}(f\times g)\circ t''_{L,M})(m, A) = \mathcal{K}(f\times g)(\downarrow\!\!m\times A) = \overline{(f\times g) (\downarrow\!\!m\times A)} = \overline{f(\downarrow\!\!m)\times g(A)} \mathrm{and},\\ (t''_{L^{'},M^{'}}\circ f\times \mathcal{K}(g))(m, A) = t''_{L^{'},M^{'}}(f(m), \overline{g(A)}) = \downarrow\!\!f(m)\times \overline{g(A)}, \end{align*}
\begin{align*} (\mathcal{K}(f\times g)\circ t''_{L,M})(m, A) = \mathcal{K}(f\times g)(\downarrow\!\!m\times A) = \overline{(f\times g) (\downarrow\!\!m\times A)} = \overline{f(\downarrow\!\!m)\times g(A)} \mathrm{and},\\ (t''_{L^{'},M^{'}}\circ f\times \mathcal{K}(g))(m, A) = t''_{L^{'},M^{'}}(f(m), \overline{g(A)}) = \downarrow\!\!f(m)\times \overline{g(A)}, \end{align*}
we just need to show
![]() $\overline{f(\downarrow\!\!m)\times g(A)} = \downarrow\!\!f(m)\times \overline{g(A)}$
. Obviously,
$\overline{f(\downarrow\!\!m)\times g(A)} = \downarrow\!\!f(m)\times \overline{g(A)}$
. Obviously,
![]() $\overline{f(\downarrow\!\!m)\times g(A)}\subseteq\;\downarrow\!\!f(m)\times \overline{g(A)}$
. On the contrary, for any
$\overline{f(\downarrow\!\!m)\times g(A)}\subseteq\;\downarrow\!\!f(m)\times \overline{g(A)}$
. On the contrary, for any
![]() $x\in \overline{g(A)}$
and
$x\in \overline{g(A)}$
and
![]() $U\in \sigma(L'\times M')$
with
$U\in \sigma(L'\times M')$
with
![]() $(f(m), x)\in U$
. Set
$(f(m), x)\in U$
. Set
![]() $U_{f(m)} = \{y\in M': (f(m),y)\in U\}$
. Then,
$U_{f(m)} = \{y\in M': (f(m),y)\in U\}$
. Then,
![]() $x\in U_{f(m)}$
and
$x\in U_{f(m)}$
and
![]() $U_{f(m)}\in \sigma({M'})$
. As
$U_{f(m)}\in \sigma({M'})$
. As
![]() $x\in \overline{g(A)}$
,
$x\in \overline{g(A)}$
,
![]() $U_{f(m)}\cap g(A) \neq \emptyset$
, which implies that there exists a
$U_{f(m)}\cap g(A) \neq \emptyset$
, which implies that there exists a
![]() $y_{0}\in U_{f(m)}\cap g(A)$
, that is,
$y_{0}\in U_{f(m)}\cap g(A)$
, that is,
![]() $(f(m), y_{0})\in (f(\downarrow\!\!m)\times g(A))\cap U\neq\emptyset$
. This means
$(f(m), y_{0})\in (f(\downarrow\!\!m)\times g(A))\cap U\neq\emptyset$
. This means
![]() $(f(m), x)\in \overline{f(\downarrow\!\!m)\times g(A)}$
, so
$(f(m), x)\in \overline{f(\downarrow\!\!m)\times g(A)}$
, so
![]() $\downarrow\!\!f(m)\times \overline{g(A)}\subseteq \overline{f(\downarrow\!\!m)\times g(A)}$
holds.
$\downarrow\!\!f(m)\times \overline{g(A)}\subseteq \overline{f(\downarrow\!\!m)\times g(A)}$
holds.
![]() $\mathbf{Claim\ 4}$
: The four diagrams given in Definition 6.1 commute when replacing
$\mathbf{Claim\ 4}$
: The four diagrams given in Definition 6.1 commute when replacing
![]() $\mathcal T$
with
$\mathcal T$
with
![]() $\mathcal{K}$
and A, B, C with dcpos L, M, N, respectively.
$\mathcal{K}$
and A, B, C with dcpos L, M, N, respectively.
The proof of the following equations is similar to that of the above, so we omit it.
-
(i) For any
 $A\in \mathcal{K}(L)$
, where 1 is the terminal object in
$A\in \mathcal{K}(L)$
, where 1 is the terminal object in \begin{align*} (\mathcal{K}l_{L}\circ t''_{\{1\},L})(1, A) = r_{\mathcal{K}(L)}(1, A), \end{align*}
\begin{align*} (\mathcal{K}l_{L}\circ t''_{\{1\},L})(1, A) = r_{\mathcal{K}(L)}(1, A), \end{align*}
 $\mathbf {DCPO}$
.
$\mathbf {DCPO}$
.
-
(ii) For any
 $(a, b)\in L\times M$
,
$(a, b)\in L\times M$
,  \begin{align*} (t''_{L,M}\circ {\mathrm{id}}_{L}\times \eta_{M})(a, b) = \eta_{L\times M}(a, b). \end{align*}
\begin{align*} (t''_{L,M}\circ {\mathrm{id}}_{L}\times \eta_{M})(a, b) = \eta_{L\times M}(a, b). \end{align*}
-
(iii) For any
 $((a, b), A)\in (L\times M)\times \mathcal{K}(N)$
,
$((a, b), A)\in (L\times M)\times \mathcal{K}(N)$
, \begin{align*} (\mathcal{K}\alpha_{L,M,N}\circ t''_{L\times M,N})((a,b),A) = (t''_{L,M\times N}\circ {\mathrm{id}}_{L}\times t''_{M,N}\circ \alpha_{L,M,\mathcal{K}(N)})((a,b),A) . \end{align*}
\begin{align*} (\mathcal{K}\alpha_{L,M,N}\circ t''_{L\times M,N})((a,b),A) = (t''_{L,M\times N}\circ {\mathrm{id}}_{L}\times t''_{M,N}\circ \alpha_{L,M,\mathcal{K}(N)})((a,b),A) . \end{align*}
-
(iv) For any
 $(a, \mathcal{A})\in L\times \mathcal{K}(\mathcal{K}(M))$
,
$(a, \mathcal{A})\in L\times \mathcal{K}(\mathcal{K}(M))$
,  \begin{align*} (\mu_{L\times M}\circ \mathcal{K}t''_{L,M}\circ t''_{L,\mathcal{K}(M)})(a, \mathcal{A}) = (t''_{L,M}\circ {\mathrm{id}}_{L}\times \mu_{M})(a, \mathcal{A}). \end{align*}
\begin{align*} (\mu_{L\times M}\circ \mathcal{K}t''_{L,M}\circ t''_{L,\mathcal{K}(M)})(a, \mathcal{A}) = (t''_{L,M}\circ {\mathrm{id}}_{L}\times \mu_{M})(a, \mathcal{A}). \end{align*}
From the construction of the
![]() $s_{L,M}$
above, we can obtain the following result.
$s_{L,M}$
above, we can obtain the following result.
Corollary 6.4.
![]() $\mathcal{K}(L)\times \mathcal{K}(M) \subseteq \mathcal{K}(L\times M)$
, where
$\mathcal{K}(L)\times \mathcal{K}(M) \subseteq \mathcal{K}(L\times M)$
, where
![]() $\mathcal{K}(L)\times \mathcal{K}(M) = \{A\times B: A\in \mathcal{K}(L), B\in \mathcal{K}(M)\}$
.
$\mathcal{K}(L)\times \mathcal{K}(M) = \{A\times B: A\in \mathcal{K}(L), B\in \mathcal{K}(M)\}$
.
Proof. For any
![]() $(A, B)\in \mathcal{K}(L)\times \mathcal{K}(M)$
, we define the map
$(A, B)\in \mathcal{K}(L)\times \mathcal{K}(M)$
, we define the map
![]() $t''^{B}_{L,M}: L\rightarrow \mathcal{K}(L\times M)$
:
$t''^{B}_{L,M}: L\rightarrow \mathcal{K}(L\times M)$
:
By the proof of Proposition 6.3, we know
![]() $t''^{B}_{L,M}$
is well-defined and Scott-continuous. Thus,
$t''^{B}_{L,M}$
is well-defined and Scott-continuous. Thus,
![]() $\overline{t''^{B}_{L,M}(A)} = \overline{\{\downarrow\!\!x\times B: x\in A\}}\in\mathcal{K}(\mathcal{K}(L\times M))$
. It follows that
$\overline{t''^{B}_{L,M}(A)} = \overline{\{\downarrow\!\!x\times B: x\in A\}}\in\mathcal{K}(\mathcal{K}(L\times M))$
. It follows that
![]() $A\times B = \mu(\overline{\{\downarrow\!\!x\times B: x\in A\}})\in \mathcal{K}(L\times M)$
.
$A\times B = \mu(\overline{\{\downarrow\!\!x\times B: x\in A\}})\in \mathcal{K}(L\times M)$
.
For dcpos L and M, we calculate the cotensorial strength
![]() $t'_{L, M}: \mathcal{K}(L)\times M\rightarrow \mathcal{K}(L\times M)$
as
$t'_{L, M}: \mathcal{K}(L)\times M\rightarrow \mathcal{K}(L\times M)$
as
![]() $\ t'_{L,M}((C, x)) = C\times {\downarrow}x $
for any
$\ t'_{L,M}((C, x)) = C\times {\downarrow}x $
for any
![]() $(C, x)\in \mathcal{K}(L)\times M$
. Following the standard categorical terminology (see Kock Reference Kock1970), the strong monad
$(C, x)\in \mathcal{K}(L)\times M$
. Following the standard categorical terminology (see Kock Reference Kock1970), the strong monad
![]() $(\mathcal{K}, \eta, \mu)$
on
$(\mathcal{K}, \eta, \mu)$
on
![]() $\mathbf{DCPO}$
is commutative if
$\mathbf{DCPO}$
is commutative if
![]() $\psi$
and
$\psi$
and
![]() $\widetilde{\psi}$
agree, where
$\widetilde{\psi}$
agree, where
![]() $\psi, \widetilde{\psi}: \mathcal{K}(L)\times \mathcal{K}(M) \rightarrow \mathcal{K}(L\times M)$
are defined as follows:
$\psi, \widetilde{\psi}: \mathcal{K}(L)\times \mathcal{K}(M) \rightarrow \mathcal{K}(L\times M)$
are defined as follows:
 \begin{align*} \psi_{L,M} = \mu_{L\times M}\circ \mathcal{K}t''_{L,M}\circ t'_{L,\mathcal{K}(M)}\\ \widetilde{\psi}_{L,M} = \mu_{L\times M}\circ \mathcal{K}t'_{L,M}\circ t''_{\mathcal{K}(L),M}. \end{align*}
\begin{align*} \psi_{L,M} = \mu_{L\times M}\circ \mathcal{K}t''_{L,M}\circ t'_{L,\mathcal{K}(M)}\\ \widetilde{\psi}_{L,M} = \mu_{L\times M}\circ \mathcal{K}t'_{L,M}\circ t''_{\mathcal{K}(L),M}. \end{align*}
It is folklore that computationally, strongness of a monad together with adequacy of the corresponding denotational semantics can be used to establish contextual equivalences for effectful programs (Moggi Reference Moggi1991; Plotkin and Power Reference Plotkin and Power2001). Particularly, if
![]() $\mathcal K$
is commutative, it will carry the structure
$\mathcal K$
is commutative, it will carry the structure
![]() $\psi$
making
$\psi$
making
![]() $(\mathcal K, \eta, \mu)$
into a symmetric monoidal monad on DCPO. With this stronger commutative property, we would know that it does not matter which order two instances of the effect appear in programs.
$(\mathcal K, \eta, \mu)$
into a symmetric monoidal monad on DCPO. With this stronger commutative property, we would know that it does not matter which order two instances of the effect appear in programs.
Theorem 6.5.
![]() $\mathcal{K}$
is a commutative monad on
$\mathcal{K}$
is a commutative monad on
![]() $\mathbf{DCPO}$
.
$\mathbf{DCPO}$
.
Proof. We just need to prove that for any dcpos L, M and
![]() $(A, B)\in \mathcal{K}(L)\times \mathcal{K}(M)$
,
$(A, B)\in \mathcal{K}(L)\times \mathcal{K}(M)$
,
![]() $ (\mu_{L\times M}\circ \mathcal{K}t''_{L,M}\circ t'_{L,\mathcal{K}(M)}) (A, B) = (\mu_{L\times M}\circ \mathcal{K}t'_{L,M}\circ t''_{\mathcal{K}(L),M}) (A,B)$
, that is,
$ (\mu_{L\times M}\circ \mathcal{K}t''_{L,M}\circ t'_{L,\mathcal{K}(M)}) (A, B) = (\mu_{L\times M}\circ \mathcal{K}t'_{L,M}\circ t''_{\mathcal{K}(L),M}) (A,B)$
, that is,
For convenience, let lhs denote the left hand side of the equation and rhs the right hand side. Consider each
![]() $a\in A$
and
$a\in A$
and
![]() $B'\subseteq B$
. For any
$B'\subseteq B$
. For any
![]() $b'\in B'$
,
$b'\in B'$
,
![]() $b'\in B$
. Then,
$b'\in B$
. Then,
![]() ${\downarrow}a\times {\downarrow}b'\in \{A'\times {\downarrow}b: A'\subseteq A, b\in B\}$
, which implies
${\downarrow}a\times {\downarrow}b'\in \{A'\times {\downarrow}b: A'\subseteq A, b\in B\}$
, which implies
![]() ${\downarrow}a\times {\downarrow}b'\subseteq rhs$
. It follows that
${\downarrow}a\times {\downarrow}b'\subseteq rhs$
. It follows that
![]() ${\downarrow}a\times B' = \bigcup\{{\downarrow}a\times {\downarrow}b': b'\in B'\}\subseteq rhs$
, in other words,
${\downarrow}a\times B' = \bigcup\{{\downarrow}a\times {\downarrow}b': b'\in B'\}\subseteq rhs$
, in other words,
![]() ${\downarrow}a\times B'\in {\downarrow} rhs$
. Then
${\downarrow}a\times B'\in {\downarrow} rhs$
. Then
![]() $\overline{\{\downarrow\!\!a\times B': a\in A, B'\subseteq B\}} \subseteq {\downarrow} rhs$
, which means
$\overline{\{\downarrow\!\!a\times B': a\in A, B'\subseteq B\}} \subseteq {\downarrow} rhs$
, which means
![]() $lhs\subseteq rhs$
.
$lhs\subseteq rhs$
.
![]() $rhs\subseteq lhs$
can be proved similarly.
$rhs\subseteq lhs$
can be proved similarly.
Remark 6.6. When
![]() $\mathcal K$
is specifically taken as
$\mathcal K$
is specifically taken as
![]() $\mathcal S$
, i.e., the order-sobrification monad proposed by Ho et al. (2018), then
$\mathcal S$
, i.e., the order-sobrification monad proposed by Ho et al. (2018), then
![]() $\mathcal S$
is commutative, and the conclusion (Jia 2020, Theorem 3.6) given by Jia is generalized by Theorem 6.5.
$\mathcal S$
is commutative, and the conclusion (Jia 2020, Theorem 3.6) given by Jia is generalized by Theorem 6.5.
We conclude our paper with a brief discussion of the advantage of semantic applications of
![]() $\mathcal K$
. We have proved that each
$\mathcal K$
. We have proved that each
![]() $\mathcal K$
is a strong monad over the category DCPO, this gives rise to the structures of
$\mathcal K$
is a strong monad over the category DCPO, this gives rise to the structures of
![]() $\lambda_c$
-models considered by Moggi (Reference Moggi1989).
$\lambda_c$
-models considered by Moggi (Reference Moggi1989).
Definition 6.7. (Moggi Reference Moggi1989) A
![]() $\lambda_c$
-model over a category C with finite products is a strong monad
$\lambda_c$
-model over a category C with finite products is a strong monad
![]() $(\mathcal T, \eta, \mu)$
together with a
$(\mathcal T, \eta, \mu)$
together with a
![]() $\mathcal T$
-exponential for every pair (A, B) of objects in C, i.e., a pair
$\mathcal T$
-exponential for every pair (A, B) of objects in C, i.e., a pair
satisfying the universal property that for any object C and
![]() $f: C\times A\rightarrow \mathcal TB$
, there exists a unique
$f: C\times A\rightarrow \mathcal TB$
, there exists a unique
![]() $h: C\rightarrow {(\mathcal TB)}^A$
, denoted by
$h: C\rightarrow {(\mathcal TB)}^A$
, denoted by
![]() $\Lambda_{A, \mathcal T B}(f)$
s.t.
$\Lambda_{A, \mathcal T B}(f)$
s.t.
From the above definition, we could clearly see that each strong monad on a Cartesian closed category is a
![]() $\lambda_c$
-model. So each order-K-ification monad
$\lambda_c$
-model. So each order-K-ification monad
![]() $\mathcal K$
is a
$\mathcal K$
is a
![]() $\lambda_c$
-model by its strongness and the Cartesian closedness of
$\lambda_c$
-model by its strongness and the Cartesian closedness of
![]() $\mathbf{DCPO}$
.
$\mathbf{DCPO}$
.
Moggi gave the interpretation of a formal system called
![]() $\lambda_c$
-calculus in a
$\lambda_c$
-calculus in a
![]() $\lambda_c$
-model, which is sound and complete with respect to the interpretation. In our case,
$\lambda_c$
-model, which is sound and complete with respect to the interpretation. In our case,
![]() $\lambda_c$
-calculus is interpreted as morphisms of the Kleisli category for
$\lambda_c$
-calculus is interpreted as morphisms of the Kleisli category for
![]() $\mathcal K$
.
$\mathcal K$
.
Recall that the Hoare power construction
![]() $\mathcal H$
on the category DCPO is useful for modeling the angelic non-determinism. In particular, one can verify that
$\mathcal H$
on the category DCPO is useful for modeling the angelic non-determinism. In particular, one can verify that
![]() $\mathcal H$
is a strong monad on DCPO, so naturally, it is also a
$\mathcal H$
is a strong monad on DCPO, so naturally, it is also a
![]() $\lambda_c$
-model. As a refinement of
$\lambda_c$
-model. As a refinement of
![]() $\mathcal H$
, there are fewer morphisms in the Kleisli category of each monad
$\mathcal H$
, there are fewer morphisms in the Kleisli category of each monad
![]() $\mathcal K$
than that of
$\mathcal K$
than that of
![]() $\mathcal H$
. So some useless semantic trash could be culled if we consider using the Kleisli category of
$\mathcal H$
. So some useless semantic trash could be culled if we consider using the Kleisli category of
![]() $\mathcal K$
as semantic categories, to provide a more accurate interpretation for the programming language at hand.
$\mathcal K$
as semantic categories, to provide a more accurate interpretation for the programming language at hand.
We would end this paper with an example to illustrate that there are indeed fewer morphisms in the Kleisli category of the monad
![]() $\mathcal K$
for some particular categories of type
$\mathcal K$
for some particular categories of type
![]() $\mathrm K$
, than that of
$\mathrm K$
, than that of
![]() $\mathcal H$
.
$\mathcal H$
.
Example 6.8. Let’s take
![]() $\mathcal K$
as the order-sobrification monad
$\mathcal K$
as the order-sobrification monad
![]() $\mathcal S$
, which assigns
$\mathcal S$
, which assigns
![]() $(Irr\Gamma(L), \subseteq)$
to each dcpo L, i.e., the poset of all irreducible closed subsets of
$(Irr\Gamma(L), \subseteq)$
to each dcpo L, i.e., the poset of all irreducible closed subsets of
![]() $\Sigma L$
with the inclusion order. Clearly,
$\Sigma L$
with the inclusion order. Clearly,
![]() $\mathcal S(L)\subseteq \mathcal H(L)$
. We take a concrete dcpo
$\mathcal S(L)\subseteq \mathcal H(L)$
. We take a concrete dcpo
![]() $L = \mathbb Z\cup \{\perp\}$
with the order
$L = \mathbb Z\cup \{\perp\}$
with the order
![]() $x\leq y$
defined as
$x\leq y$
defined as
![]() $x = \perp, y\in \mathbb Z$
or
$x = \perp, y\in \mathbb Z$
or
![]() $x= y \in \mathbb Z$
, where
$x= y \in \mathbb Z$
, where
![]() $\mathbb Z$
is the set of all integers, and a dcpo
$\mathbb Z$
is the set of all integers, and a dcpo
![]() $M = \{0, 1\}$
with the usual order
$M = \{0, 1\}$
with the usual order
![]() $0\leq 1$
. In denotational semantics, L is the semantic of the type int and M is that of the type unit. Note that
$0\leq 1$
. In denotational semantics, L is the semantic of the type int and M is that of the type unit. Note that
![]() $\Gamma(L) = \{{\downarrow}A: A\subseteq \mathbb Z\}\cup\{\bot\}$
,
$\Gamma(L) = \{{\downarrow}A: A\subseteq \mathbb Z\}\cup\{\bot\}$
,
![]() $Irr\Gamma(L) = \{{\downarrow}n: n\in \mathbb Z\}\cup\{\bot\}$
. We define a map
$Irr\Gamma(L) = \{{\downarrow}n: n\in \mathbb Z\}\cup\{\bot\}$
. We define a map
![]() $f: M\rightarrow \mathcal H(L)$
as
$f: M\rightarrow \mathcal H(L)$
as
 \begin{align*} f(m) =\begin{cases} \bot,& \mathrm{m = 0}\\ {\downarrow}\{1,2\},& \mathrm{m = 1}.\end{cases} \end{align*}
\begin{align*} f(m) =\begin{cases} \bot,& \mathrm{m = 0}\\ {\downarrow}\{1,2\},& \mathrm{m = 1}.\end{cases} \end{align*}
The map f is Scott-continuous since it is monotone and M is finite; hence, it is in
![]() $\mathbf{DCPO}_{\mathcal H}$
. However, there is no Scott-continuous map
$\mathbf{DCPO}_{\mathcal H}$
. However, there is no Scott-continuous map
![]() $g: M\to \mathcal S(L)$
in
$g: M\to \mathcal S(L)$
in
![]() $\mathbf{DCPO}_{\mathcal S}$
such that
$\mathbf{DCPO}_{\mathcal S}$
such that
![]() $f = i\circ g$
, where
$f = i\circ g$
, where
![]() $i: \mathcal S(L)\rightarrow\mathcal H(L)$
is the canonical inclusion map. This is obvious because the images of
$i: \mathcal S(L)\rightarrow\mathcal H(L)$
is the canonical inclusion map. This is obvious because the images of
![]() $i\circ g$
consist of principal ideals, while f(1) is not a principal ideal.
$i\circ g$
consist of principal ideals, while f(1) is not a principal ideal.

Acknowledgements
The authors would like to thank the referee for the numerous and very helpful suggestions that have improved this paper substantially.
Competing interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.